基于季節分解和長短期記憶的北京市雞蛋價格預測

劉 雪，劉錦濤，李佳利，張小栓，張文豪

·專題論壇·

基于季節分解和長短期記憶的北京市雞蛋價格預測

劉 雪1，劉錦濤1，李佳利1，張小栓2，張文豪3

（1. 中國農業大學信息與電氣工程學院，北京 100083；2. 中國農業大學工學院，北京 100083；3. 中國農業大學經濟管理學院，北京 100083）

準確把握北京市場雞蛋價格波動特征和規律，及時預測雞蛋價格波動趨勢，不僅是農業進入新發展階段的首都“菜籃子”工程建設的需要，而且有利于社會經濟的穩定發展。該文選取北京市月度雞蛋價格作為試驗數據，在對北京市雞蛋價格歷史數據分析的基礎上，根據雞蛋價格序列的非線性、季節性和周期性特征，提出一種基于時間序列季節性分解（Seasonal-trend Decomposition Procedure Based on Loess，STL）和長短期記憶網絡（Long-short Term Memory，LSTM）組合的雞蛋價格預測模型。通過采用LSTM模型實現對由STL方法分解的雞蛋價格波動成分的趨勢成分及剩余成分和用季節樸素方法（Seasonal-na?ve, Sna?ve）對雞蛋價格波動的季節成分分別進行預測，可以獲取未來雞蛋價格的綜合預測值。研究結果表明：2000—2018年北京市雞蛋價格在整體呈現上升趨勢，且存在“春低秋高”的季節性和隨機波動特征；該研究構建的STL-LSTM模型在預測步長分別為1、3、6時的均方根誤差分別為0.19、0.33、0.43；平均絕對百分比誤差分別為1.91、3.53、4.58，均優于長短期記憶網絡、支持向量回歸（Support Vector Regression，SVR）和差分整合移動平均自回歸（Autoregressive Integrated Moving Average Model，ARIMA）模型，可以為預測預警北京市場雞蛋價格異常波動情況、為行業和政府主管部門保障北京市場雞蛋供應決策提供參考依據。

動物；雞蛋；季節性分解；長短期記憶網絡；價格預測

0 引 言

雞蛋營養價值豐富，含有人體必需的蛋白質、脂肪、膽固醇、氨基酸等營養物質和微量元素，幾乎適宜所有人食用，是公認的人體攝取蛋白質重要來源。同時，由于雞蛋價格波動頻繁、波動幅度大[1]，雞蛋價格一直是社會各界關注的熱點。據農業部監測數據顯示，2000年至2015年中國雞蛋價格出現了14次小周期波動、7次大周期波動；特別2007年以來，中國雞蛋價格波動愈發頻繁[2]。北京市場也不例外，近年來，尤其是在首都功能定位以及疏解促提升的大背景下，北京市蛋雞產業發展的空間和數量不斷壓縮，北京市的雞蛋價格波動更是呈現出波動頻率高和波動幅度大的特點，雞蛋價格最高時為11.96元/kg，最低時為5.3元/kg，波動幅度高達125%。頻繁的價格波動不僅增加了行業人員生產、銷售、決策的難度和風險，也影響了首都居民的生活質量和北京的社會和經濟穩定。因此在新的發展階段，在雞蛋自給率不斷下降的情況下，急需加強對國際性大都市北京市場雞蛋價格波動特征及其規律的分析，并及時、準確地對北京雞蛋市場價格未來走勢及供應進行研判。

圍繞農產品價格，國內外開展了廣泛的研究，主要涉及價格波動特征與規律[3-7]、影響價格的因素[8-11]與價格預測[12-15]等方面。首先是價格波動特征與規律方面的研究。Henry等（1930年）[16-18]分別提出了關于生產和商品價格波動，形成蛛網理論的雛形，對農產品價格研究具有劃時代的意義，并不斷得到進一步的擴展和完善。其次是關于影響價格因素的研究。供給和需求無疑是影響農產品價格的根本原因，但是農產品的流通環節、國家政策、市場因素和能源等通過影響供求，并進而影響農產品價格波動[19-21]。最后學者們普遍關注的農產品價格方面的就是農產品價格預測，隨著大數據和智能計算的發展，農產品價格預測將得到更快的進展。

從研究對象上，針對不同農產品價格的研究已經相當廣泛，如玉米[22-23]、大豆[24-25]、蔬菜[26-27]、生豬[28-29]及雞蛋[30-32]等。從研究方法上，學者們一直在進行不懈的探索。CensusX12季節調整方法、HP濾波（high-pass filter）及BP濾波（band-pass filter）等方法是廣泛用以對價格波動及其特征規律進行分析，并證明可以較好地對農產品價格波動的長期趨勢、季節性、周期性及隨機波動特征進行分析總結[33-35]；多元回歸和向量自回歸模型等方法常用來確定影響價格的主要因素及影響程度[36-38]；價格預測研究常用的預測模型有回歸分析模型[39-41]、時間序列模型[42-43]及組合模型[44-47]。回歸分析模型依據價格波動與其影響因子相關的原理，選擇影響貢獻率較高的因子建立回歸模型進行預測；時間序列模型依據價格數據與時間的關系對未來的價格進行預測，該方法對線性價格數據具有較好的預測效果，但對非線性數據預測效果較差；組合模型能夠較好地結合農產品特性及其價格波動特征，構建相應的模型對未來的價格進行預測。

可見，價格問題一直是學術界研究和關注的熱門問題，已有的研究已然非常豐富，但仍存在一定的問題和不足：首先是大都關注大田作物和大宗農產品，雖然有學者開展了對雞蛋價格的研究，但也主要關注全國雞蛋價格，鮮有針對區域和國際性大都市雞蛋價格的研究；第二，目前關于雞蛋價格的研究往往將價格波動特征與預測分割開來，造成價格預測的解釋性較差。第三，在結合價格波動特征進行預測模型的構建與優化方面尚顯不足。基于以上思考，本文在對北京市雞蛋價格數據進行分解處理的基礎上，提出一種基于時間序列季節性分解方法（Seasonal-trend Decomposition Procedure Based on Loess，STL）和長短期記憶網絡（Long-short Term Memory，LSTM）組合的雞蛋價格預測模型STL-LSTM，分析北京市雞蛋價格波動特征及其規律，并及時并準確把握新發展階段北京市場雞蛋價格未來走勢。本研究結果和結論可以為政府、行業管理部門和從業人員決策提供參考，并為其他農產品價格分析和預測提供可借鑒的思路和方法。

1 數據與方法

1.1 數據

1.1.1 數據來源

集貿市場是指城鄉居民進行農副產品、日用消費品等現貨商品交易或固定地點買賣貨物的市場。北京市集貿市場主要分為居民社區周邊的菜市場為主的小型集市和集零售批發為一體的大型農貿市場。集貿市場所售賣的雞蛋面向普通居民、企事業單位、學校、酒店等場所，其價格可以直觀反映對銷售者和消費者的影響，并間接對生產者進行反饋。因此本文根據中國畜牧信息網（http://www.caaa.cn/）收集的價格數據進行分析。本次試驗數據范圍為2000年1月至2018年12月，數據樣本數為228條，其價格單位為元/kg。此次研究將2000年1月至2017年12月連續216個月的價格數據用于模型訓練，2018年1月至2018年12月連續12個月的價格數據作為預測樣本，和2018年12個月的真實數據進行比較，以驗證模型預測的準確性。

1.1.2 北京市雞蛋價格特征

2000年1月至2018年12月期間，北京雞蛋價格總體波動中保持上升（圖1a），2014年10月份左右雞蛋價格達到最高點，隨后在波動中稍有下降。考察整個價格區間，雞蛋價格大體每28~36個月會呈現出一個倒U型的波動周期。但近年來，雞蛋價格波動出現了新的變化：雞蛋價格上升趨勢不再明顯，而是上下波動頻繁；雞蛋價格波動周期開始縮短，波動的幅度也越來越大。

北京雞蛋價格有著明顯的隨季節變化的波動規律。將北京雞蛋價格2000—2018年月度價格數據進行分割，按照每36個月為一組，共分為6組數據（圖1b）。可以發現北京雞蛋價格波動有著明顯的季節性。每年的2、3月份雞蛋價格開始下降，4、5月份雞蛋價格降至低點，6、7月份之后雞蛋價格逐漸回升，9、10月份雞蛋價格達到全年高點。圖2中各時間段的價格序列大體保持平行，表明北京雞蛋價格的季節性波動并非偶然現象，且已多年表現出季節性波動特征。

圖1 北京市雞蛋價格

1.2 方法

1.2.1 價格預測方法

根據上述雞蛋價格序列的非線性、季節性和周期性波動特征，提出了基于時間序列季節性分解方法（Seasonal-trend Decomposition Procedure Based on Loess，STL）和長短期記憶網絡（Long-short Term Memory，LSTM）組合的雞蛋價格預測模型STL-LSTM。首先對于給定的雞蛋價格序列，通過STL模型將原始雞蛋價格序列分解為趨勢成分、季節成分和剩余成分3部分。其次用LSTM模型對分解后的雞蛋價格波動趨勢成分和剩余成分預測，季節樸素方法（Seasonal-na?ve, Sna?ve）對分解后的季節成分預測。最后，將預測得出的雞蛋價格趨勢成分預測值、剩余成分預測值和季節成分預測值相加求和，得到原始雞蛋價格預測值（圖2）。

圖2 雞蛋價格預測流程

1.2.2 結果驗證方法

本文選取了相對誤差（Relative Error，RE），均方根誤差（Root Mean Square Error，RMSE）以及平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）來評測預測模型的準確性，其各自計算公式如下

2 模型構建

2.1 雞蛋價格STL分解模型

STL是一種時間序列分解方法，由Cleveland等發展的時間序列數據的濾波季節分解方法，可以穩健處理任何類型的季節性數據[48]。STL與傳統季節性分解技術（例如X-12-ARIMA和移動平均比率方法）不同，其在處理時間序列數據時少數異常觀測值不會影響模型對趨勢周期和季節性因素的估計。

2.2 STL模型參數選擇

依照Cleveland等的研究和雞蛋價格序列的特征[48-49]，對參數進行如下設置。

使用RStudio軟件環境中“stats”庫中的STL函數完成分解任務。

2.3 雞蛋價格LSTM預測的模型

2.3.1 LSTM模型原理

LSTM（Long-short Term Memory）長短期記憶網絡是由Hochreiter等提出的一種時間循環神經網絡，通過對傳統循環神經網絡（Recurrent Neural Network，RNN）的改進，解決了標準RNN的梯度消失問題，實現信息的長期記憶。目前，LSTM模型已經成為深度學習框架中廣為應用的預測模型，在很多領域應用效果突出[50-52]。

注：x、y分別表示輸入和輸出序列，i、f、c和o分別表示為時刻的輸入門、遺忘門和輸出門，∫為激活函數。

Note: x,yare the vector sequences of input units and output units, respectively. i,f,candoare the input gate, forget gate and output gate, respectively. In addtion, ∫ is activation functions.

圖3 長短期記憶網絡基本結構

Fig.3 Structure of long-short term memory

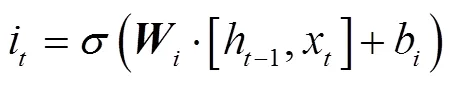
最終，由輸出門確定輸出雞蛋價格的預測值

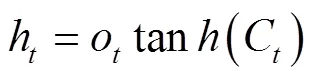
2.3.2 LSTM模型搭建

本次研究的程序開發環境為Jupyter Notebook（python 3.7），使用Keras提供的LSTM神經網絡模型。結合雞蛋價格序列分解后的趨勢序列和剩余序列特征及LSTM的設計原則，本次研究的LSTM模型包括輸入層、隱藏層和輸出層3個基本模塊。輸入層對雞蛋價格的趨勢序列和剩余序列進行初步的處理以滿足模型輸入的要求；隱藏層構建LSTM細胞鏈路形成網絡；輸出層獲得預測結果。

輸入層和輸出層：本次研究用前6個月的數據預測未來1個月的價格數據。輸入變量分別依次為雞蛋價格的趨勢成分和剩余成分；輸出層輸出變量個數為下個月單個變量。因此，輸入層和輸出層神經元個數為1。

隱藏層：關于如何選取隱藏層層數及其神經元數，目前還沒有普遍被認可的方法。一般認為，通過增加隱藏層神經元數來獲得較低的誤差，要比增加隱藏層數更易實現。考慮到本次研究數據序列的長度，本次選用2個隱藏層，同時每層設置50個神經元，共計100個神經元。

參數設置：當訓練次數為100時，模型的損失基本不在下降。因此，訓練次數為100；損失函數選擇較為常用的均方誤差（mse）函數；優化器選擇Adam 算法，該算法實現簡單，計算效率高，內存需求小。

2.4 多步預測的迭代策略

分別以1、3和6個月的時間步長進行試驗，因此需要建立一個多步預測的LSTM模型。迭代策略是多步預測模型中最為常見的一種策略，并且該策略已經廣泛應用到各領域的預測中[53-55]。

以此類推，可以進行多步長預測，以獲取多步預測值。

3 結果與分析

3.1 雞蛋價格波動特征

雞蛋價格的季節性序列顯示了“春低秋高”的季節性特征，并呈現出為期12個月左右的循環周期（圖4）。具體表現為每年的雞蛋價格在春季（3、4月）一般為全年的最低值，隨后5月份開始回升，并且一般在在秋季（9、10月）達到全年的最高值，11月份再次下降，12月份到次年1月份小幅度回升后下降。如此循環往復，呈現出為期12個月左右的季節波動周期。蛋雞產蛋的季節性規律是雞蛋價格季節性波動的重要原因。春季溫度和濕度較為適宜蛋雞的生產，此時蛋雞生產效率提升，市場上雞蛋供給逐步上升，使得雞蛋價格開始下降。6月份左右氣溫升高雞蛋產量開始減少，加之下半年節假日對于雞蛋消費需求的刺激，使得市場上雞蛋價格開始回升。

雞蛋價格的趨勢序列反映了剔除雞蛋價格季節性成分和剩余成分后雞蛋價格長期變動的真實趨勢。從趨勢序列可以看出，2000年以來雞蛋價格趨勢序列整體呈現出明顯的上升趨勢，上升幅度約為132.14%。但是2014年之后雞蛋價格趨勢序列上升趨勢不明顯，而是經歷小幅下降之后再次上升。雞蛋價格的長期趨勢呈現為上升曲線主要原因為：中國經濟社會的快速發展，人民收入水平不斷提高，對雞蛋的消費需求隨之增加；蛋雞養殖所用的人工、飼料、土地和水電等價格成本提高。

雞蛋價格剩余成分序列波動表現出隨機性，且波動幅度有所增大。雞蛋價格剩余成分序列與季節序列不同，并未表現出明顯的規律性，上下波動起伏不定。2000年以來大幅異常價格波動主要發生在2003、2011以及2014年前后。2003年SARS疫情、2010年甲型H1N1型流感以及2013年H7N9禽流感是造成雞蛋價格大幅異常波動的主要原因。疫情爆發首先引起消費者對雞蛋需求的下降和雞蛋價格的大幅下跌，然后蛋雞養殖行業整體虧損，養殖戶補欄減少甚至退出蛋雞養殖行業，導致蛋雞存欄的減少和雞蛋產能大幅下降，導致雞蛋的生產供給與市場需求存在偏差，最終使得雞蛋價格出現異常價格波動。

圖4 雞蛋價格序列分解結果

3.2 雞蛋價格波動來源

總體而言，趨勢成分是雞蛋價格波動的主要貢獻因素。通過計算協方差，可以進一步分析趨勢成分、季節成分和剩余成分對雞蛋價格波動的貢獻率。

根據式（4）所得結果進行協方差計算，各成分貢獻率為

雞蛋價格各分量波動貢獻率如表1所示。各成分橫向對比來看，趨勢成分一直是雞蛋價格波動的主要貢獻因素，季節成分的貢獻率次之，剩余成分對雞蛋價格波動的長期影響相對較小；時間縱向對比來看，趨勢成分對于雞蛋價格波動的貢獻率在逐漸下降，季節和剩余成分對雞蛋價格波動的貢獻率在上升。

表1 各分量對雞蛋價格波動的貢獻率

3.3 雞蛋價格預測結果

STL-LSTM模型預測結果和實際雞蛋價格波動規律特征基本相符，表現出良好的預測效果。每年的2—5月份，雞蛋呈現價格下降趨勢，6、7月份后雞蛋價格開始呈現上升趨勢，在9、10月份基本達到一年的價格最高峰。11、12月份雞蛋價格呈現緩慢下降趨勢，1、2月份雞蛋價格再次上升，迎來一次價格小高峰，全年雞蛋價格走勢基本類似為“M”型。如圖5所示，STL-LSTM模型的預測結果基本圍繞雞蛋價格走勢上下波動，表現出良好的預測效果。

圖5 STL-LSTM模型預測雞蛋價格結果與真值比較

對雞蛋價格各序列成分進行分析，獲取更多的數據特征，并選擇相應的預測模型，是增加最終預測精度的關鍵。首先，3個序列的預測誤差被有效降低時，特別是趨勢序列成分的預測誤差降低時，最終的預測結果將會更加接近實際值。因為，雞蛋價格趨勢序列成分是雞蛋價格波動的主要貢獻因素，其預測精度的高低將最大程度的決定預測效果的精度。其次，相對于趨勢序列成分，季節序列成分和剩余序列成分的預測雖然更為復雜和困難，但是2種成分對雞蛋價格波動貢獻率較低。所以，選取契合其數據特征的季節樸素方法和LSTM模型進行預測。一方面降低了對2種序列的預測誤差，另一方面該2種成分作為雞蛋價格波動的次要貢獻因素，其所產生的誤差反饋到雞蛋價格時也會隨之降低。最終，將3種成分的預測結果相加求和，以達到良好的預測效果。

3.4 雞蛋價格預測評價

將STL-LSTM模型預測得出的2018年12個月的雞蛋價格數值列出并與真實雞蛋價格數據進行對比分析。由表2可知，2018年12個月的雞蛋價格預測結果與實際值相比誤差較小。當預測步長分別為1、3和6時，預測的相對誤差（Relative Error，RE）保持在3.67%、6.49%和7.22%以下，均方根誤差（Root Mean Square Error，RMSE）分別為0.19、0.33和0.43，平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）分別為1.91、3.53和4.58，預測效果良好。

為了更好的體現STL-LSTM模型的預測效果，本文同時使用了基于時間序列的LSTM模型、SVR模型和ARIMA模型對北京雞蛋價格進行預測，預測結果如圖6所示。由表3可知不同預測模型所得出的2018年12個月的北京雞蛋價格預測性能。當預測步長=1時，STL-LSTM預測模型的預測結果相較于LSTM模型，RMES和MAPE分別降低了27.05%和21.45%；相較于SVR模型，RMES和MAPE分別降低了32.87%和37.96%；相較于ARIMA模型，RMES和MAPE分別降低了58.94%和55.93%。當預測步長=3時，STL-LSTM預測模型的預測結果相較于LSTM模型，RMES和MAPE分別降低了8.26%和2.68%；較于SVR模型，RMES和MAPE分別降低了26.34%和28.39%；相較于ARIMA模型，RMES和MAPE分別降低了51.35%和50.36%。當預測步長=6時，STL-LSTM預測模型的預測結果相較于LSTM模型，RMES和MAPE分別降低了10.75%和9.03%；相較于SVR模型，RMES和MAPE分別降低了14.05%和14.67%；相較于ARIMA模型，RMES和MAPE分別降低了45.15%和39.51%。由此表明，本文提出的STL-LSTM模型無論是在單步預測還是多步預測中均有良好的預測效果。

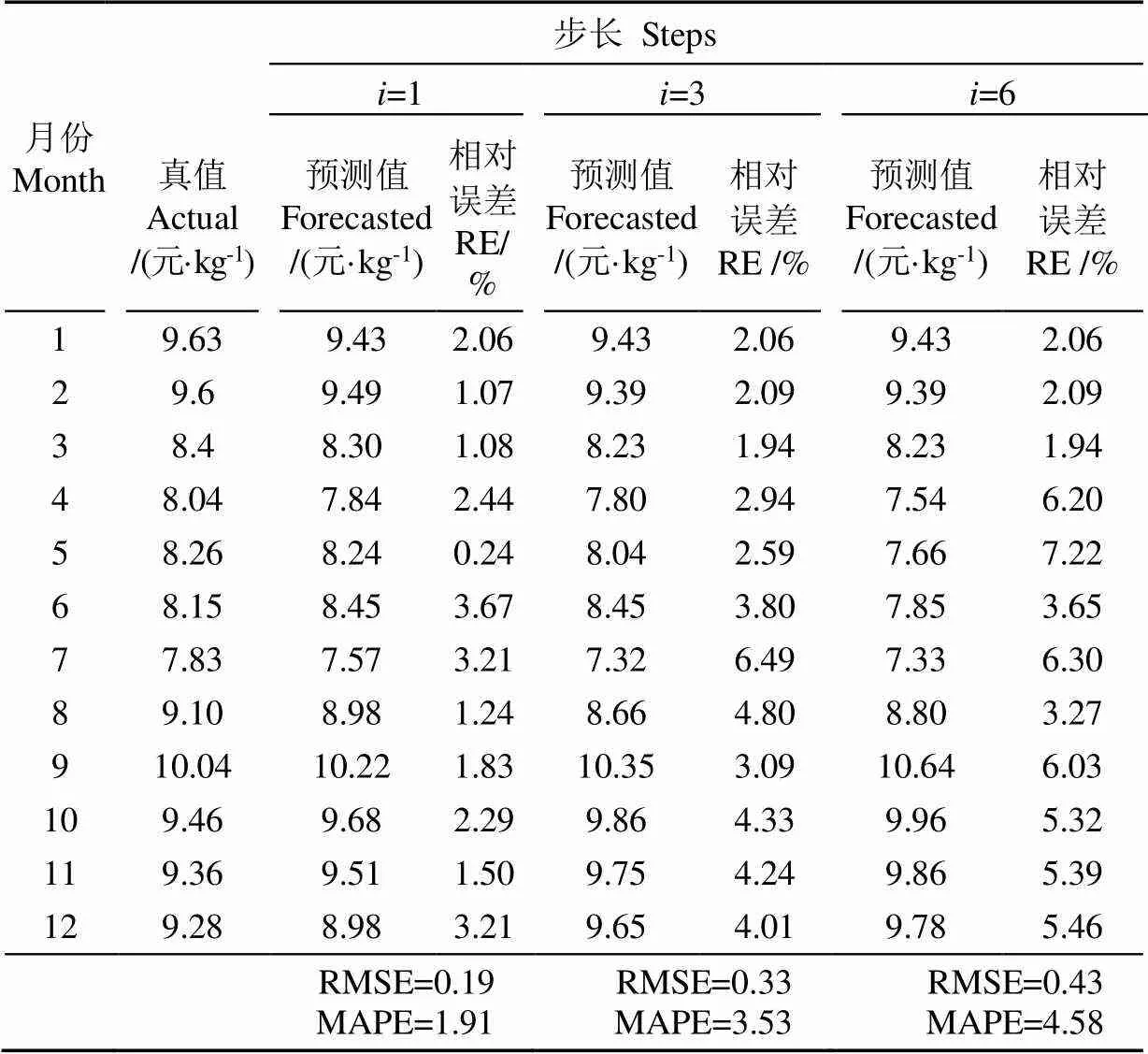
表2 雞蛋價格STL-LSTM模型預測值和實際值對比

圖6 基于時間序列的STL-LSTM、LSTM、SVR、ARIMA模型的預測結果對比

表3 不同模型雞蛋價格預測結果對比

相對于LSTM、SVR和ARIMA預測模型，STL-LSTM組合模型有著更為突出的優勢。首先，LSTM、SVR和ARIMA此類單模型在進行價格預測時并未對價格數據進行先驗處理，無法很好的擬合雞蛋價格波動中的季節性和周期性，因而在最終的價格預測中存在一定的預測困難。因此，先驗數據處理并獲取更多的數據特征對于建立良好的預測模型是非常重要的。其次，在對比的3種模型中，ARIMA始終是在所有預測步長下預測效果最差的模型。其一大原因是，ARIMA模型是典型的線性預測模型，對于非線性特征的雞蛋價格序列預測會產生較大的偏差。而STL-LSTM組合模型則充分考慮了這上述2方面的問題。在對雞蛋價格數據進行分解，獲得更多的數據特征的基礎上，選擇更為合適的預測模型進行預測。最終有效的降低了預測誤差，表現出更為良好的預測效果。

4 結 論

本文構建了一種基于時間序列季節性分解和長短期記憶網絡組合的預測模型STL-LSTM，分析了北京市雞蛋價格變動特征并進行價格預測，主要研究結論如下：

1）采用STL分解北京市雞蛋價格，分析得出2000—2018年北京市雞蛋價格整體呈現上升趨勢，上升幅度約為132.14%，且存在周期約12個月的“春低秋高”的季節性波動和隨機價格波動。

2）雞蛋價格波動可分解為趨勢成分、季節成分和剩余成分。其中，雖然隨著時間推移其貢獻率由71.18%下降到56.84%，趨勢成分仍然是影響雞蛋價格波動的主要原因；季節成分和剩余成分近年來對雞蛋價格的影響增大，其貢獻率分別由26.56%和2.24%提升至34.24%和8.92%。

3）本文提出的STL-LSTM模型解決了傳統預測方法預測精度低和解釋性差等問題，預測準確度高。對不同預測步長1、3、6，本文提出的STL-LSTM模型預測結果的均方根誤差分別為0.19、0.33、0.46，平均絕對百分比誤差分別為1.91、3.53、4.58，均優于單獨的LSTM、SVR和ARIMA模。

本文提出的STL-LSTM模型具有良好的預測性能和泛化能力，可以為預測預警北京市場雞蛋價格異常波動情況、為行業和政府主管部門保障北京市場雞蛋供應決策提供參考依據。

[1] Wu Yuhuan, Qin Fu. Analysis of egg price fluctuation and cause[J]. Journal of Agricultural Science, 2018, 10(11): 581-587.

[2] 周榮柱，秦富. 蛋雞生產與雞蛋價格動態變化關系[J]. 中國農業大學學報，2016，21(10)：145-154. Zhou Rongzhu, Qin Fu. Research on dynamic change correlations between the production performance of laying hen and egg price[J]. Journal of China Agricultural University, 2016, 21(10): 145-154. (in Chinese with English abstract)

[3] Suci Miranda, Vembri Noor Helia. Quantitative analysis on the fluctuation of vegetable price in supermarket[J]. MATEC Web of Conferences, 2018, 154(5): 182-186.

[4] 羅千峰，張利庠. 基于B-N分解法的我國生豬價格波動特征研究[J]. 農業技術經濟，2018，7：93-106. Luo Qianfeng, Zhang Lixiang. Fluctuation characteristics of hog price in China: Evidence based on the method of B-N decomposition[J]. Journal of Agrotechnical Economics, 2018, 7: 93-106. (in Chinese with English abstract)

[5] 徐明凡，劉合光. 關于我國雞蛋價格的預測及分析[J]. 統計與決策，2014，6：106-109. Xu Mingfan, Liu Heguang. Prediction and analysis of egg prices in China[J]. Statistics & Decision, 2014, 6: 106-109. (in Chinese with English abstract)

[6] 譚銀清，王釗，陳益芳. 我國雞蛋價格波動的特點及影響因素分析[J]. 畜牧與獸醫，2015，47(1)：125-129. Tan Yinqing, Wang Zhao, Chen Yifang. Analysis of the characteristics and influencing factors of egg price fluctuation in China[J]. Animal Husbandry & Veterinary Medicine, 2015, 47(1): 125-129. (in Chinese with English abstract)

[7] 武玉環，秦富. 當前我國雞蛋價格趨勢的分析及預測[J]. 價格理論與實踐，2017，10：110-113. Wu Yuhuan, Qin Fu. Analysis and forecast of egg price in China[J]. Price: Theory & Practice, 2017, 10: 110-113. (in Chinese with English abstract)

[8] 楊玉影，郝小瑤，劉安軒，等. 我國雞蛋價格波動特點及影響因素研究[J]. 黑龍江畜牧獸醫，2018，2：14-19. Yang Yuying, Hao Xiaoyao, Liu Anxuan, et al. Study on the characteristics and influential factors of egg price fluctuation in China[J]. Heilongjiang Animal Science and Veterinary Medicine, 2018, 2: 14-19. (in Chinese with English abstract)

[9] 陳寧，楊文靜. 我國豬肉價格波動及其影響因素分析：基于Markov區制轉換VAR模型的實證檢驗[J]. 中國畜牧雜志，2016，52(20)：51-56. Chen Ning, Yang Wenjing. Analysis on the fluctuation on pork prices and its influencing factors in China empirical research based on the model of markov mechanism switching VAR[J]. Chinese Journal of Animal Science, 2016, 52(20): 51-56. (in Chinese with English abstract)

[10] 鄭旭蕓，莊麗娟，邱澤慧. 中國玉米價格分布及波動影響因素的實證[J]. 統計與決策，2020，2：52-56. Zheng Xuyun, Zhuang Lijuan, Qiu Zehui. Empirical study on maize price distribution and its influencing factors in China[J]. Statistics & Decision, 2020, 2: 52-56. (in Chinese with English abstract)

[11] 朱海燕，司偉. 中國小麥價格波動影響因素分析[J]. 農業技術經濟，2015，5：47-58. Zhu Haiyan, Si Wei. Analysis on the influencing factors of Chinese wheat price fluctuation[J]. Journal of Agrotechnical Economics, 2015, 5: 47-58. (in Chinese with English abstract)

[12] Davenport F, Funk C. Using time series structural characteristics to analyze grain prices in food insecure countries[J]. Food Security, 2015, 7(5): 1055-1070.

[13] 周應堂，賈馥蔚，溫焜. 我國小麥價格短期預測研究：基于APSO-SVR模型的分析[J]. 價格理論與實踐，2018，3：107-110. Zhou Yingtang, Jia Fuwei, Wen Kun. Study on short-term wheat price prediction in China: Analysis based on APSO-SVR model[J]. Price: Theory & Practice, 2018, 3: 107-110. (in Chinese with English abstract)

[14] 孫建明. 基于能繁母豬存欄量和豬糧價比的豬肉價格預報[J]. 農業工程學報，2013，29(13)：1-6. Sun Jianming. Pork price forecast based on breeding sow stocks and hog-grain price ratio[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(13): 1-6. (in Chinese with English abstract)

[15] Xu Longqin, Liu Shuangyin. Study of short-term water quality prediction model based on wavelet neural network[J]. Mathematical & Computer Modelling, 2013, 58(3/4): 807-813.

[16] Henry Schultz. Der Sinn der statistischen Nachfragekurven[M]. Bonn: Kurt Schroeder Verlag, 1930.

[17] Tinbergen J. Bestimmung und deutung von angebotskurven ein beispiel[J]. Zeitschrift Für Nationalkonomie, 1930, 1(5): 669-679.

[18] Ricci U. Die, synthetische ?konomie" von Henry Ludwell Moore[J]. Ztschrift für Nationalkonomie, 1930, 1(5): 649-668.

[19] 楊思雨，田國強. 農產品批發價格指數與物流業景氣指數的關系研究[J]. 中國農業大學學報，2020，25(4)：162-171. Yang Siyu, Tian Guoqiang. Research on the relationship between wholesale price index of agricultural products and logistics prosperity index[J]. 2020, 25(4): 162-171. (in Chinese with English abstract)

[20] 陳迪欽，漆雁斌. 中國生豬價格波動影響因素的實證分析[J]. 湖北農業科學，2013，52(4)：959-963. Cheng Diqin, Qi Yanbin. Empirical analysis on the factors affecting price fluctuation of live pig in China[J]. Hubei Agricultural Sciences, 2013, 52(4): 959-963. (in Chinese with English abstract)

[21] 宮斌斌，劉文明，楊寧，等. 吉林省玉米價格波動及其影響因素分析[J]. 玉米科學，2017，25(2)：148-151. Guo Binbin, Liu Wenming, Yang Ning, et al. Analysis on the influencing factors of corn price in Jilin province[J]. Journal of Maize Sciences, 2017, 25(2): 148-151. (in Chinese with English abstract)

[22] Xu Xiaojie. Using local information to improve short-run corn price forecasts[J]. Journal of Agricultural & Food Industrial Organization, 2018, 16(1): 1-15.

[23] David E Kenyon. Producer ability to forecast harvest corn and soybean prices[J]. Review of Agricultural Economics, 2001, 23(1): 151-162.

[24] 朱婧，范亞東，徐勇. 基于改進GM(1，1)模型的中國大豆價格預測[J]. 大豆科學，2016，35(2)：315-319. Zhu Jing, Fang Yadong, Xu Yong. Soybean price prediction in China based on modified GM(1, 1) model[J]. Soybean Science, 2016, 35(2): 315-319. (in Chinese with English abstract)

[25] 石波，張冬青，馬開平，等. 改進RBF神經網絡在我國大豆價格預測中的應用研究[J]. 大豆科學，2016，35(2)：310-314. Shi Bo, Zhang Dongqing, Ma Kaiping, et al. Soybean price prediction in China based on improved RBF neural network[J]. Soybean Science, 2016, 35(2): 310-314. (in Chinese with English abstract)

[26] Yercan M, Adanacioglu H. An analysis of tomato prices at wholesale level in Turkey: An application of SARIMA model[J]. Custos E Agronegocio, 2012, 8(4): 52-75.

[27] Yang Lei, Li Kangshun, Zhang Wensheng, et al. Short-term vegetable prices forecast based on improved gene expression programming[J]. International Journal of High Performance Computing and Networking, 2018, 11(3): 199-213.

[28] 蔡超敏，凌立文，牛超，等. 國內豬肉市場價格的EMD-SVM集成預測模型[J]. 中國管理科學，2016，24(1)：845-851. Cai Chaomin, Ling Liwen, Niu Chao, et al. Intergration prediction of domestic pork market price based on empirical mode decomposition and support vector machine[J]. Chinese Journal of Management Science, 2016, 24(1): 845-851. (in Chinese with English abstract)

[29] 平平，劉大有，楊博，等. 組合預測模型在豬肉價格預測中的應用研究[J]. 計算機工程與科學，2010，32(5)：109-112. Ping Ping, Liu Dayou, Yang Bo, et al. Research on the combinational model for predicting the pork price[J]. Computer Engineering & Science, 2010, 32(5): 109-112. (in Chinese with English abstract)

[30] Li Zhemin, Cui Liguo, Xu Shiwei, et al. Prediction model of weekly retail price for eggs based on chaotic neural network[J]. Journal of Integrative Agriculture, 2013, 12(12): 2292-2299.

[31] 唐江橋. 中國雞蛋價格波動周期識別與短期預測[J]. 中國畜牧雜志，2017，53(5)：142-148. Tang Jiangqiao. China egg price fluctuation cycle identification and short-term forecast[J]. Chinese Journal of Animal Science, 2017(5): 142-148. (in Chinese with English abstract)

[32] 牛東來，陳連頤，程子珍. 基于BP神經網絡的北京市農產品批發市場雞蛋價格短期預測研究[J]. 中國家禽，2017，39(24)：35-40. Niu Donglai, Chen Lianyi, Cheng Zizhen. Study on short-term forecast of egg price in beijing agricultural products wholesale market based on on BP neural network[J]. China Poultry, 2017, 39(24): 35-40. (in Chinese with English abstract)

[33] 閆振宇，孫養學. 我國雞蛋價格波動規律及影響因素分析[J]. 統計與決策，2018，34(19)：150-154. Yan Zhenyu, Sun Yangxue. Analysis of the fluctuation law and influencing factors of egg price in China[J]. Statistics & Decision, 2018, 34(19): 150-154. (in Chinese with English abstract)

[34] 劉訓翰，張利庠，楊海霞. 中國畜產品價格的實證分析：基于季節調整模型與兩階段協方差方法[J]. 經濟與管理研究，2015，36(4)：39-44. Liu Xunhan, Zhang Lixiang, Yang Haixia. Empirical analysis of livestock prices in China: based on seasonal adjustment model and tow-stage covariance method[J]. Research on Economics and Management, 2015, 36(4): 39-44.

[35] 戴煒，胡浩，虞祎. 我國肉雞市場價格周期性波動分析[J]. 農業技術經濟，2014(5)：12-20. Dai Wei, Hu Hao, Yu Yi. Analysis of cyclical price fluctuations in China broiler market[J]. Journal of Agrotechnical Economics, 2014(5): 12-20. (in Chinese with English abstract)

[36] 陳瓊，王濟民. 基于VAR模型的我國雞肉價格波動的影響因素分析[J]. 中國畜牧雜志，2013，49(10)：23-28. Chen Qiong, Wang Jimin. Analysis on the influencing factors of chicken price fluctuation in China based on VAR model[J]. Chinese Journal of Animal Science, 2013, 49(10): 23-28. (in Chinese with English abstract)

[37] 黨紅旗，閆強強. 基于多元回歸的糧食價格影響因素分析[J]. 農村經濟與科技，2017，28(15)：132-133. Dang Hongqi, Yan Qiangqiang. Analysis of factors influencing food prices based on multiple regression[J]. Rural Economy and Science-Technology, 2017, 28(15): 132-133. (in Chinese with English abstract)

[38] 盧彥丞，許畔. 基于Markov區制轉換VAR模型的我國雞肉價格波動及其影響因素分析[J]. 中國家禽，2018，40(1)：36-41. Lu Yancheng, Xu Pan. Markov mechanism switch vector autoregressive model for price fluctuation and its influence factors[J]. China Poultry, 2018, 40(1): 36-41. (in Chinese with English abstract)

[39] 任青山，方逵，朱幸輝. 基于多元回歸的BP神經網絡生豬價格預測模型[J]. 江蘇農業科學，2019，47(14)：277-281. Ren Qingshan, Fang Kui, Zhu Xinghui. Prediction model of hog price based on BP neural network and multiple regression[J]. Jiangsu Agricultural Sciences. 2019, 47(14): 277-281. (in Chinese with English abstract)

[40] Li Ganqiong, Xu Shiwei, Li Zhemin, et al. Using quantile regression approach to analyze price movements of agricultural products in china[J]. Journal of Integrative Agriculture, 2012, 11(4): 674-683.

[41] 胡晟，肖深根. 基于自回歸積分滑動平均模型的玉竹價格預測分析[J]. 湖南農業科學，2018，399(12)：96-100. Hu Sheng, Xiao Shen’gen. Analysis of price forecasting of polygonatum odoratum based on ARIMA model[J]. Hunan Agricultural Sciences, 2018, 399(12): 96-100. (in Chinese with English abstract)

[42] Pandian A S S, Kumar G S, Prabu M, et al. Time series analysis of wholesale and retail egg prices in major market centres of South India[J]. Indian Journal of Animal Research, 2011, 45(1): 38-42.

[43] Tarjei K. A time series spot price forecast model for the nord pool market[J]. Electrical Power and Energy Systems, 2014, 61: 20-26.

[44] Xiong T, Li C, Bao Y. Seasonal forecasting of agricultural commodity price using a hybrid STL and ELM method: Evidence from the vegetable market in China[J]. Neurocomputing, 2018, 275(1): 2831-2844.

[45] 段青玲，張磊，魏芳芳，等. 基于時間序列GA-SVR的水產品價格預測模型及驗證[J]. 農業工程學報，2017，33(1)：308-314. Duan Qingling, Zhang Lei, Wei Fangfang, et al. Forecasting model and validation for aquatic product price based on time series GA-SVR[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(1): 308-314. (in Chinese with English abstract)

[46] Jumah A, Kunst R M. Seasonal prediction of European cereal prices: Good forecasts using bad models?[J]. Journal of Forecasting, 2008, 27(5): 391-406.

[47] Ramirez O A, Fadiga M L. Forecasting agricultural commodity prices with asymmetric-error GARCH models[J]. Journal of Agricultural and Resource Economics, 2003, 28(1): 71-85.

[48] Cleveland R, Cleveland W, McRae J, et al. STL: A seasonal-trend decomposition procedure based on loess[J]. Journal of Official Statistics 1990, 6(1): 3-33.

[49] Bergmann I, Ramillien G, Frappart F. Climate-driven interannual ice mass evolution in Greenland[J]. Global and Planetary Change, 2012, 82/83: 1-11.

[50] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780.

[51] Navares R, Aznarte J. Predicting air quality with deep learning LSTM: Towards comprehensive models[J]. Ecological Informatics, 2019, 55: 10-19.

[52] 石曉文，蔣洪迅. 面向高精度與強魯棒的空氣質量預測LSTM模型研究[J]. 統計與決策，2019，35(16)：49-53. Shi Xiaowen, Jiang Hongxun. LSTM-based air quality index predicting model for accuracy and robustness[J]. Statistics & Decision, 2019, 35(16): 49-53. (in Chinese with English abstract)

[53] Jha G K, Sinha K. Time-delay neural networks for time series prediction: an application to the monthly wholesale price of oilseeds in India[J]. neural computing & applications, 2014, 24(3/4): 563-571.

[54] Xiong T, Bao Y, Hu Z. Multiple-output support vector regression with a firefly algorithm for interval-valued stock price index forecasting[J]. Knowledge-Based Systems, 2014, 55(1): 87-100.

[55] Bao Y, Xiong T, Hu Z. PSO-MISMO modeling strategy for multistep-ahead time series prediction[J]. IEEE Transactions On Cybernetics, 2014, 44(5): 655-668.

Egg price forecasting in Beijing market using seasonal-trend decomposition procedures based on seasonal decomposition and long-short term memory

Liu Xue1, Liu Jintao1, Li Jiali1, Zhang Xiaoshuan2, Zhang Wenhao3

(1.,,100083,; 2.,,100083,; 3.,,100083,)

Egg price has been attracting public attentions from every community in Beijing market. It is necessary to obtain timely information for the ?uctuation of the future egg price, particularly on the demand and supply of table eggs for human consumption. A lot of efforts have been made to accurately forecast future egg price in short, medium or long terms. However, there are many factors affecting egg prices to make the prediction challenging. In this paper, a hybrid model was proposed to forecast egg price by combining seasonal-trend decomposition procedures based on loess (STL) and long short-term memory (LSTM), denoted as STL-LSTM. In decomposition, a time series can be splitted into three components: seasonality, trends and remainder fluctuation. A more stable variance can be obtained from the non-linear, seasonal and periodic each part of egg price. Then, LSTM can be used to capture appropriate behaviors and predict precisely the trends and remainder parts of egg price, respectively, while the seasonal-na?ve method can be used to predict seasonal trends in a 12-month cycle. The results from three parts were summarized into a total price forecast. The egg price data that used in this study were collected from the China animal husbandry, covering from January 2000 to December 2018 in Beijing egg markets. The monthly data from January 2000 to December 2017 were used as training set, whereas the 12 monthly data in 2018 were used as testing set in the proposed model. The method was evaluated by using the relative error (RE), root mean square error (RMSE) and the mean absolute error percentage (MAPE). The results show that there was an overall upward trend for the egg price in the Beijing market from January 2000 to December 2018, with the seasonal fluctuation of “low spring and high autumn”, and random fluctuations. The decomposition indicated that the trend component was the main contributor to egg price fluctuations, where the contribution rate decreased from 71.18% to 56.84% during the test period. The influence of seasonal and remaining components on egg prices increased in recent years, with the contribution rates of 34.24% and 8.92%, respectively. In STL-LSTM model, when the step size was given as 1, 3 and 6, the evaluating indexes were optimum: the relative error of 3.67%, 6.49% and 7.22%, the root mean square errors of 0.19, 0.33, and 0.43, and the average absolute percentage errors of 1.91, 3.53, and 4.58. In terms of the evaluating indexes, the proposed STL-LSTM model demonstrated most efficiency to predict egg prices, compared with the previous models, such as separate LSTM, support vector regression (SVR) and the autoregressive integrated moving average (ARIMA). The proposed model can be expected to extend on price predictions of other similar agricultural product in the future. The findings can provide a great potential to accurately forecast the future egg price for market strategies in animal husbandry.

animals; eggs; seasonal decomposition; long-short term memory; price prediction

劉雪，劉錦濤，李佳利，等. 基于季節分解和長短期記憶的北京市雞蛋價格預測[J]. 農業工程學報，2020，36(9)：331-340.doi：10.11975/j.issn.1002-6819.2020.09.038 http://www.tcsae.org

Liu Xue, Liu Jintao, Li Jiali, et al. Egg price forecasting in Beijing market using seasonal-trend decomposition procedures based on seasonal decomposition and long-short term memory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(9): 331-340. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.09.038 http://www.tcsae.org

2019-12-16

2020-04-17

現代農業產業技術體系北京市家禽創新團隊建設項目（BAIC04–2020）

劉雪，博士，副教授，研究方向：農業信息管理、物流與供應鏈管理，Email：liusnow@cau.edu.cn

10.11975/j.issn.1002-6819.2020.09.038

304.2；TP301.6

A

1002-6819(2020)-09-0331-10