基于多節點模型的液態熔鹽堆堆芯功率控制

姜慶豐，曾文杰，謝金森，朱偉聰

(南華大學 核科學技術學院，湖南 衡陽 421001)

堆芯功率控制系統的設計技術是核反應堆控制、運行的重要課題。多節點堆芯建模方法是在反應堆點堆建模方法的基礎上形成的。利用該方法所建立的多節點模型可用于堆芯功率控制系統的設計研究。多節點堆芯建模方法已受到研究者們的廣泛關注，并被積極用于堆芯功率控制系統設計研究。例如，為研究模塊式球床高溫氣冷堆堆芯控制系統特性，Dong等人[1]建立了十節點堆芯數學模型。為搭建AP1000機械補償控制的Matlab/Simulink仿真平臺，Wang等人[2]建立了堆芯多節點模型。為利用LQG/LTR(Linear Quadratic Gaussian with Loop Transfer Recovery)控制設計堆芯功率控制系統，Li[3]建立了堆芯雙節點模型。

液態熔鹽堆中，主泵驅動燃料熔鹽在主回路系統中流動，采用控制棒控制堆芯功率。杜尚勉等人[4]基于堆芯線性化模型，采用LQG/LTR設計液態熔鹽堆堆芯功率控制系統。本文基于熔鹽實驗堆MSRE(Molten salt reactor experiment)的實驗測量數據[5,6]，采用多節點堆芯建模方法，建立MSRE的九節點堆芯模型。在此模型基礎上，為實現MSRE堆芯功率控制，以PID(Proportional-Integral-Derivative)控制技術設計堆芯功率控制系統，開展堆芯反應性擾動等工況下的控制仿真，并將多節點模型下的仿真結果與點堆模型下的結果進行比較和分析。

1 堆芯多節點模型

熔鹽實驗堆堆芯活化區由正方形結構的石墨組件構成，兩個石墨塊之間的凹槽形成了熔鹽燃料流動通道[7]。將熔鹽實驗堆MSRE堆芯劃分為9個節點區域，如圖1所示[6]。采用微分方程組描述所有區域內相應的狀態變量，考慮到堆芯燃料的流動特性，引入時間延遲項，建立堆芯多節點模型。在建立堆芯多節點模型前，先做如下假設：

(1)在短時間內可以不考慮堆芯內碘氙等毒物的產生，因此，忽略碘氙等毒物效應。同時，假設燃料流動為不可壓縮流動，不考慮燃料鹽中的循環空隙率產生的反應性效應。將單個節點區域內的換熱過程描述為單個節點區域內兩個燃料節塊與一個石墨節塊的換熱過程，如圖2所示。最終堆芯系統被劃分為18個燃料節塊和9個石墨節塊；

(2)考慮到熔鹽實驗堆中石墨中產生的熱量較少，且石墨中徑向和軸向的分布較為均勻，因此，不考慮堆芯石墨中徑向和軸向的傳熱。假設堆芯節點區域中，每個燃料節塊內燃料混合良好，流出燃料節塊的液相溫度與節塊內液相溫度相同；

(3)在堆芯多節點劃分中，將堆芯燃料熔鹽入口流量徑向劃分為4個不同的質量流量流入堆芯，使得燃料熔鹽在堆芯中的平均停留時間與堆芯單節點模型相同。

1.1 堆芯物理模型

考慮燃料熔鹽在堆芯中的流動效應，建立堆芯物理模型[5,6]。

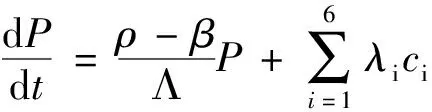
(1)

(2)

公式(2)中[5]，

(3)

(4)

公式(4)中，

公式(1)～公式(4)中：

P——反應堆功率；

ci——第i組緩發中子先驅核密度；

t——時間；

ρ——引入堆芯的總反應性；

β——有效緩發中子總份額；

βi——第i組緩發中子份額；

λi——第i組緩發中子先驅核衰減常數；

Λ——堆內中子代時間；

τc、τl——熔鹽燃料在堆內的流動時間和堆外的流動時間。

對公式(1)、公式(4)兩式進行歸一化處理，

(5)

(6)

公式(5)、公式(6)中：

Pr(t)=P(t)/P0——堆芯相對功率；

cir(t)=ci(t)/ci0——第i組緩發中子先驅核相對密度；

P0、c0——堆芯初始穩態功率、堆芯初始穩態先驅核濃度。

1.2 堆芯傳熱模型

針對堆芯某一節點區域，依據圖2所示劃分節塊。基于堆芯燃料熔鹽和石墨的能量守恒，建立堆芯單個節點內的傳熱模型。假設燃料節塊內燃料混合良好，流出燃料節塊的液相溫度與節塊內液相溫度相同，考慮單個節點區域功率值占堆芯總功率權重，通過建立每個節點中的傳熱模型并進行聯立，建立堆芯多節點傳熱模型[5，6]。

(7)

(8)

(9)

式中:下標j——堆芯節點號:

Tjf1、Tjf2、Tjin——堆芯節點j中燃料節塊1、節塊2的平均溫度及節點的燃料入口溫度；

Tjg——堆芯節點j中石墨平均溫度；

τjf1、τjf2——堆芯節點j中，熔鹽燃料流過燃料節塊1、節塊2的流動時間；

mf1、mf2——堆芯單個節點中燃料節塊1、節塊2的質量；

mg——堆芯單個節點中的石墨質量；

K1、K2——單個節點中燃料節塊1、節塊2產生的堆芯功率份額；

Kg1、Kg2——堆芯單個節點中石墨節塊傳遞給燃料節塊1、燃料節塊2的功率份額；

Cpf——燃料的定壓比熱容；

Cpg——石墨的定壓比熱容；

U——燃料和冷卻劑間的換熱系數。

堆芯燃料的平均溫度Tjf為：

1.3 堆芯反應性模型

液態熔鹽堆中，堆芯的總反應性可以表示為[5,6]:

ρ(t)=ρ0+ρfb(t)+ρrod(t)

(10)

公式(10)中，

(11)

堆芯溫度反應性反饋主要來源于每個節點內的燃料溫度反饋和石墨溫度反饋。考慮到每個燃料節塊或石墨節塊對堆芯系統的溫度反饋的貢獻不同，引入權重值I。堆芯總的溫度反饋反應性計算式如下:

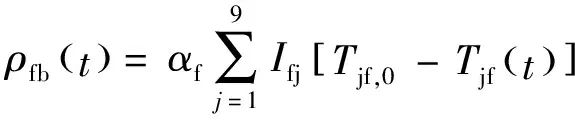
(12)

式中:ρ0——堆芯穩態初始反應性；

ρfb——堆芯9個節點的溫度反饋反應性；

ρrod——控制棒引入的反應性；

αf、αg——燃料熔鹽溫度反饋系數和石墨溫度反饋系數；

Tjf,0、Tjg,0——表示穩態初始時刻燃料熔鹽平均溫度和石墨平均溫度。

2 堆芯功率控制器設計

2.1 堆芯傳遞函數模型

選取控制棒反應性作為輸入量，以堆芯相對功率作為輸出量，定義堆芯模型的狀態變量、輸入變量和輸出變量分別為：

xr=[δPr,δc1r,δc2r,δc3r,δc4r,δc5r,δc6r,δT1f1,δT1f2,δT1g,δT2f1,δT2f2,δT2g,δT3f1,δT3f2,δT3g,……,δT8f1,δT8f2,δT8g,δT9f1,δT9f2,δT9g]

ur=[δρrod]

yr=[δPr]

在某一穩態工作點，對堆芯多節點模型線性化后可得堆芯線性狀態空間模型，并將其轉換為單輸入單輸出的堆芯傳遞函數模型：

[δPr]=Gr(s)[δρrod]

2.2 堆芯功率控制器設計

在設計堆芯功率控制器之前，先做如下簡化處理：(1)棒位變化量和其引入的反應性之間的關系用線性函數Kr表示，即控制棒每步引入的反應性為常量；(2)棒速程序單元是一個非線性單元，為了簡化控制器的設計，暫不考慮死區、磁滯回環及最小和最大棒速值，僅將其作為一個增益為Kc的線性環節。設計的棒控系統如圖3所示。

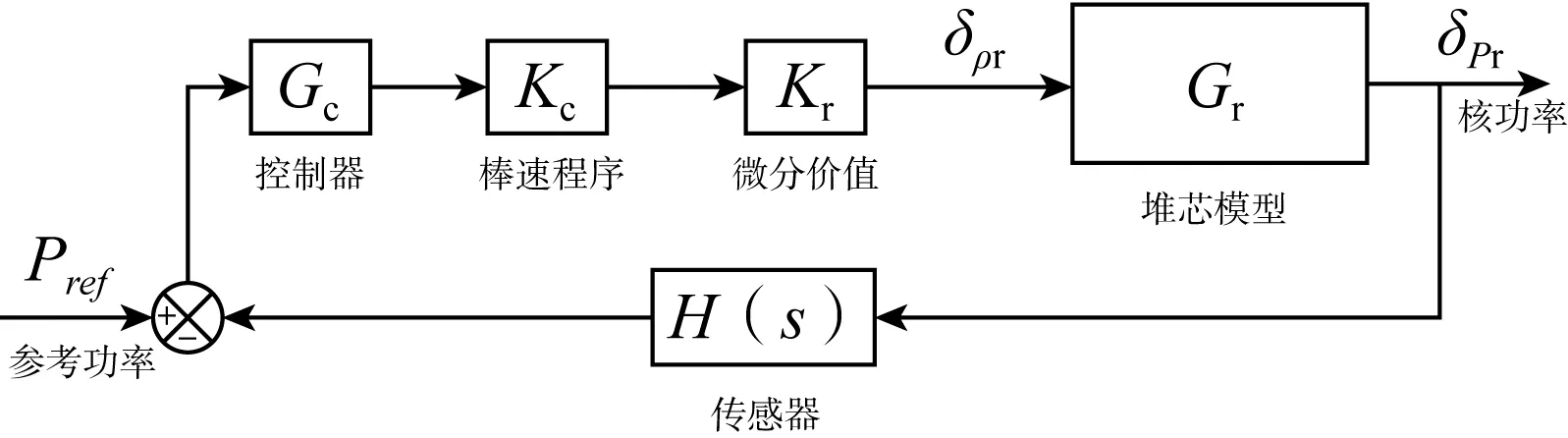
圖3 基于核功率反饋控制的棒控系統

基于堆芯線性化模型，以MSRE堆芯為例，采用Matlab[8]軟件編制程序進行堆芯功率PID控制計算。

3 堆芯功率控制仿真

3.1 研究對象

為了驗證Th—U循環，熔鹽實驗堆MSRE利用233U做燃料開展了試驗。本文以233U燃料堆芯為對象，其堆芯的主要設計參數如表1所示[4,5]。堆芯中包含4根控制棒，控制棒采用中空圓柱體，用于堆芯功率控制。MSRE堆芯9節點區域參數見表2所示[5]。233U的中子物理學參數如表3所示。

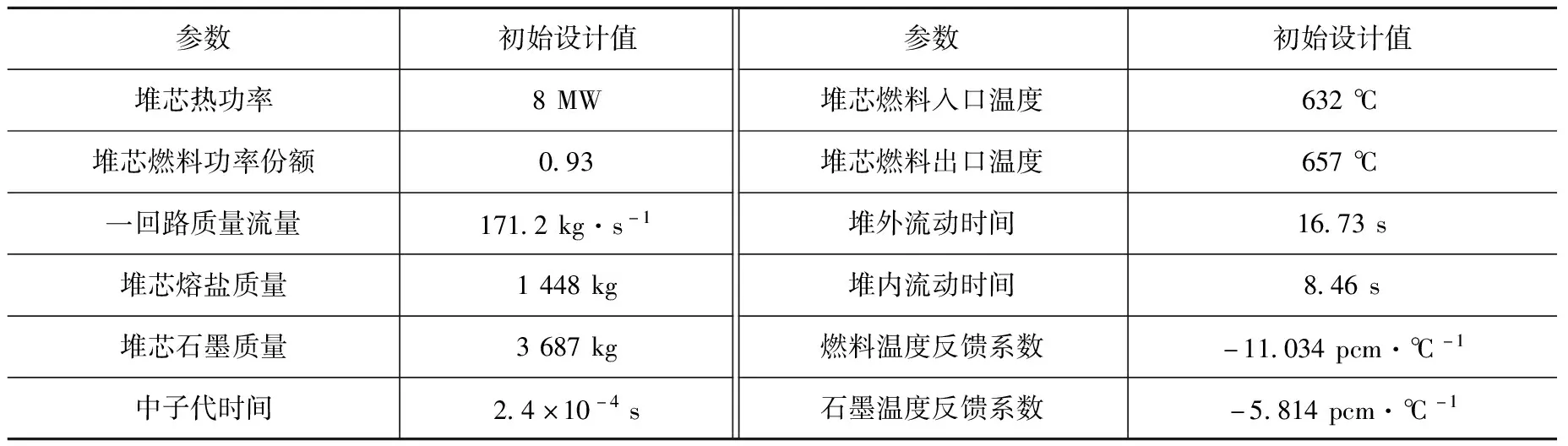
表1 MSRE堆芯的主要設計參數[4,5]

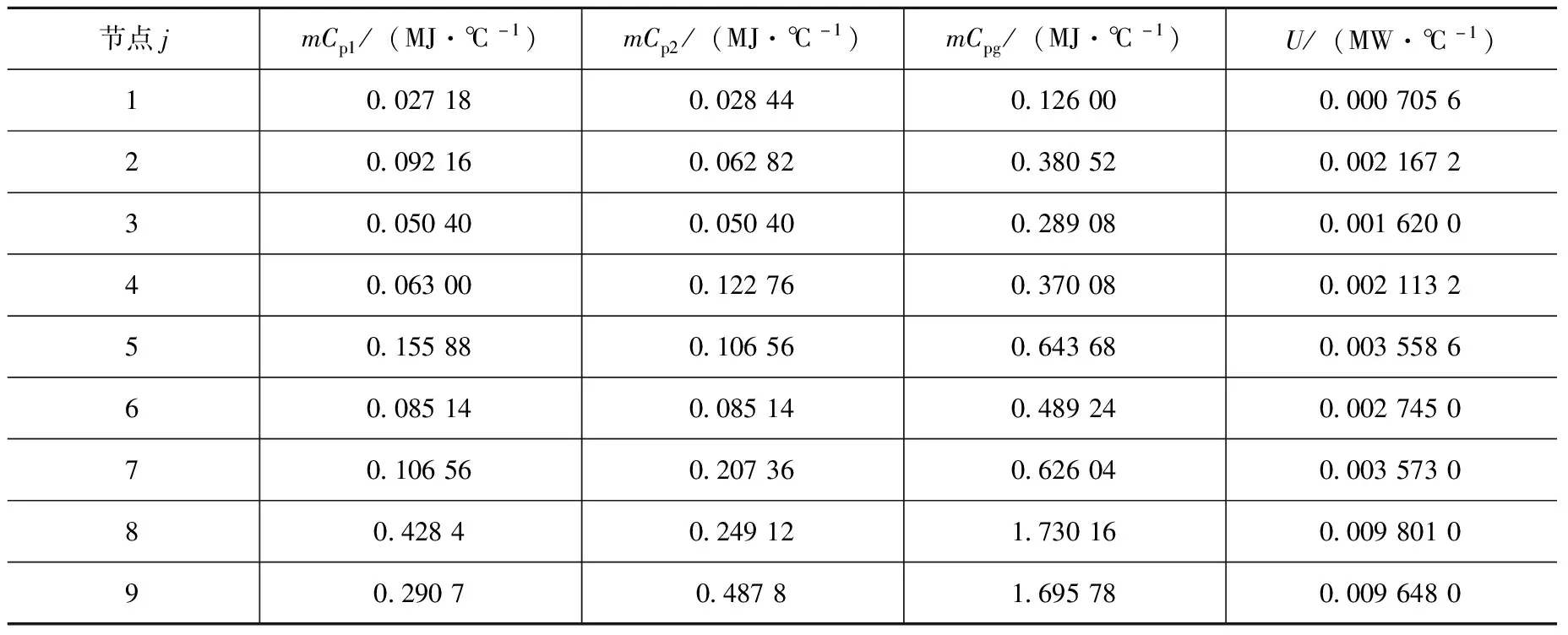
表2 MSRE堆芯9節點區域參數[5]

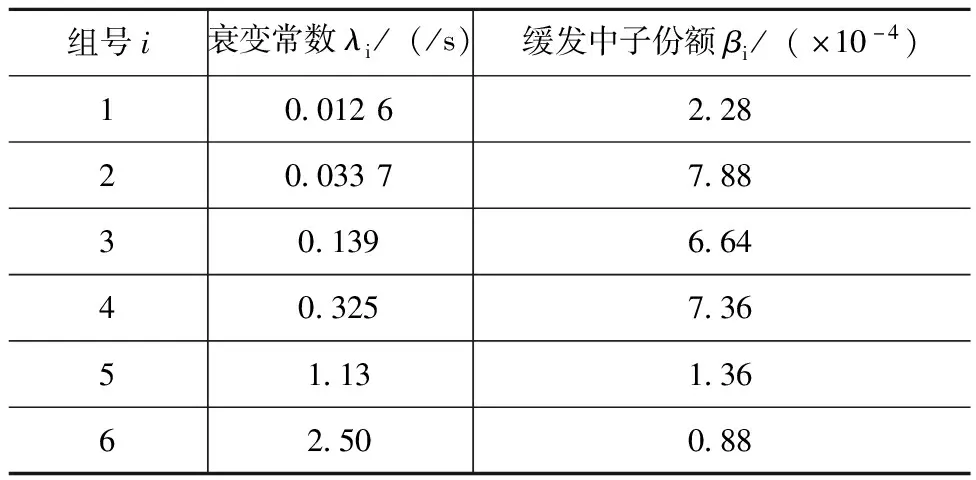
表3 233U燃料堆芯中子物理學參數[5]

3.2 堆芯功率控制仿真

對于裝載233U燃料的MSRE系統在1 MW、5 MW、8 MW三種功率水平下階躍引入10 pcm的反應性，仿真結果如圖4所示。由圖可知，在不加控制器的情況下，當系統引入反應性擾動時，系統功率超調量較大，調節時間較長。系統功率在經歷上沖后，依靠燃料和石墨溫度負反饋，相對功率(實際功率與相應堆芯功率的比值)偏差逐漸穩定在一個新的輸出值上。在增加PID控制器的情況下，系統響應的上沖幅度減小，過渡時間較短。系統經歷短暫上沖后最后穩定在一個比無控制器下的幅度小得多新的輸出值。

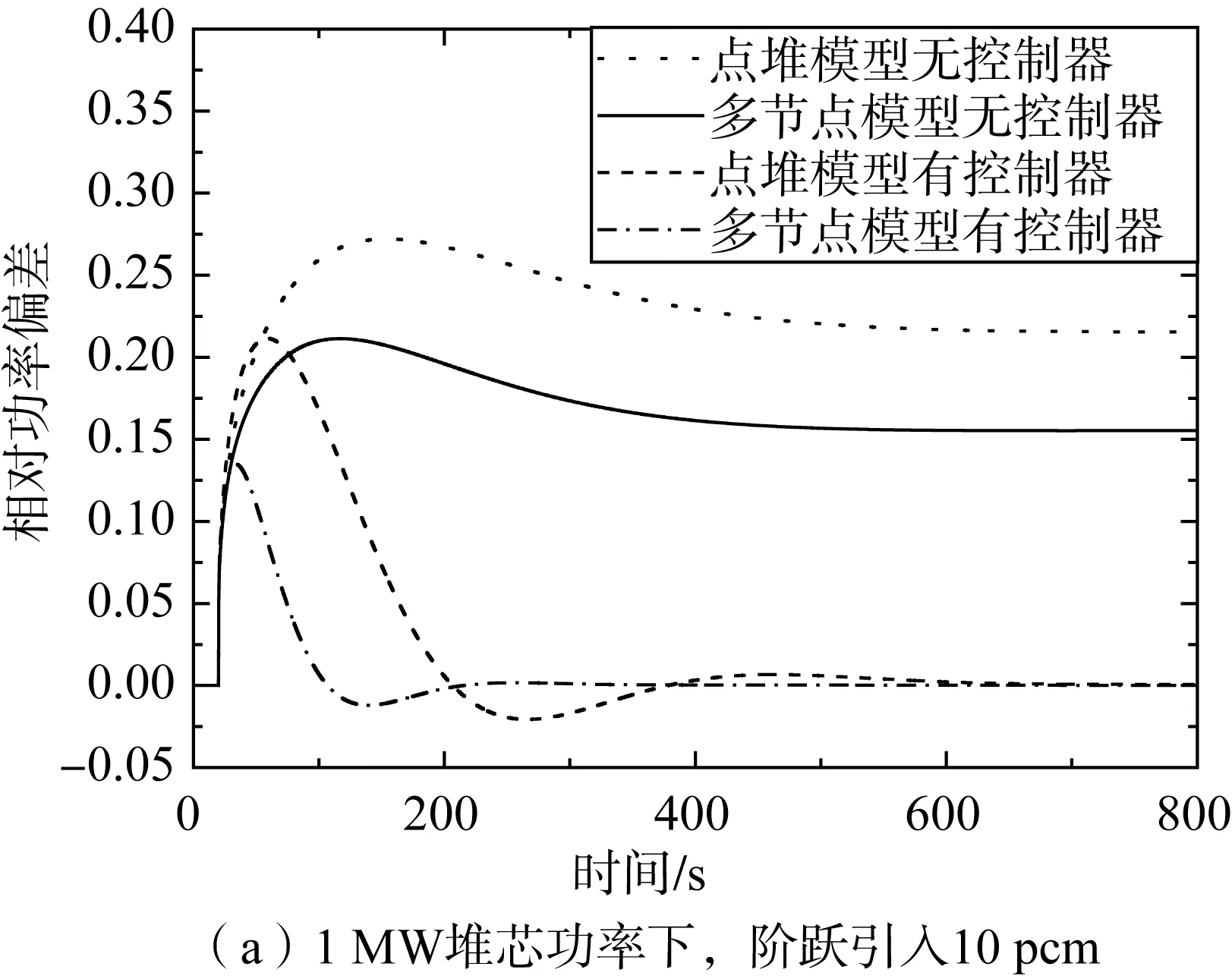
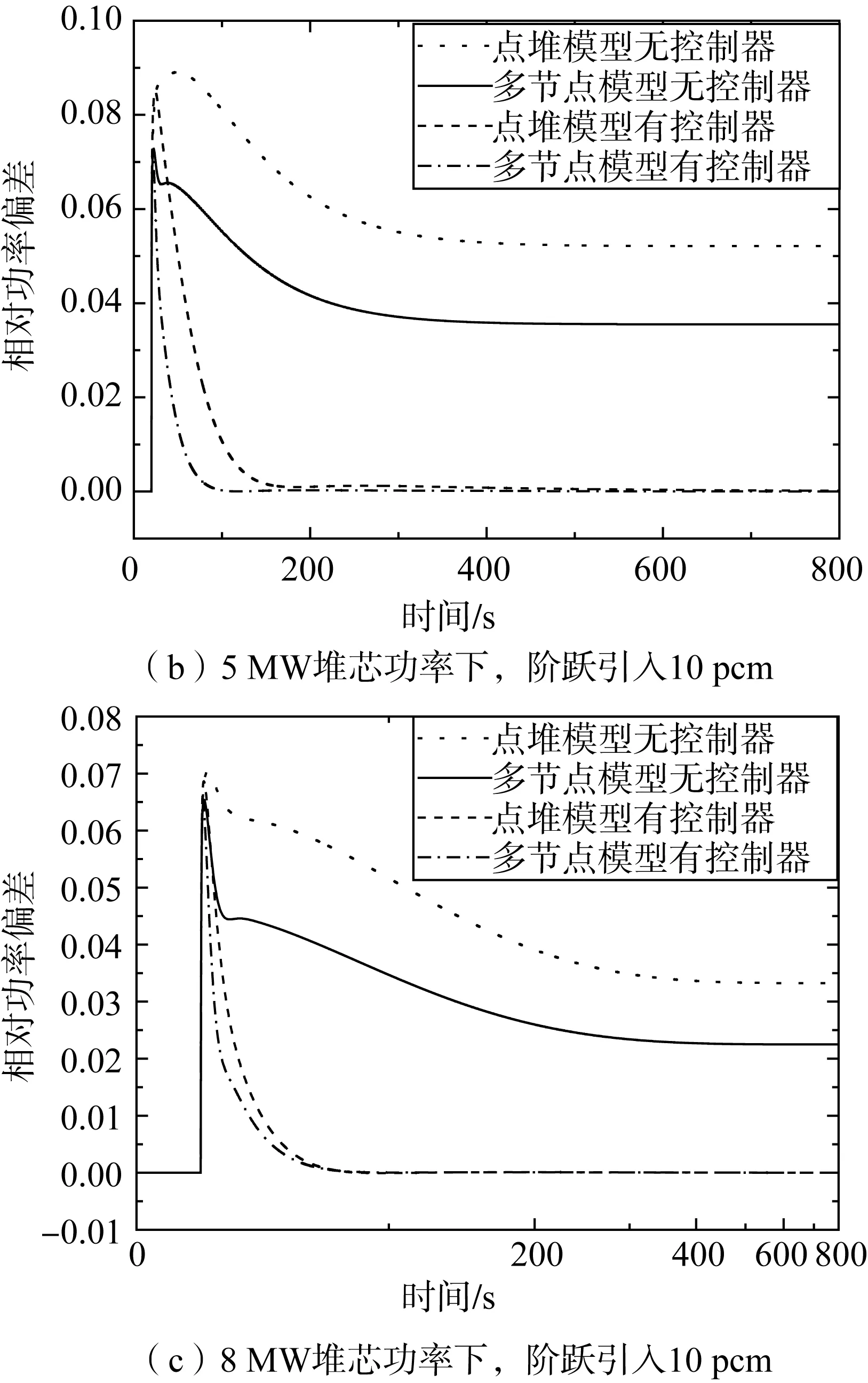
圖4 引入10 pcm反應性，堆芯功率PID控制響應曲線

在1 MW、5 MW、8 MW功率水平下階躍引入50 pcm反應性，仿真結果如圖5所示。圖中可以看出，在反應性階躍引入后功率立即有瞬間躍升，最后都穩定在一個穩定值，變化趨勢同階躍引入10 pcm反應性大致相似。由此可見，對于液態熔鹽堆堆芯系統，基于堆芯多節點模型設計的PID功率控制器可以實現對反應性擾動的良好控制。

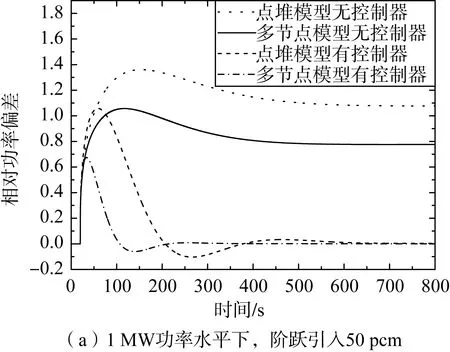
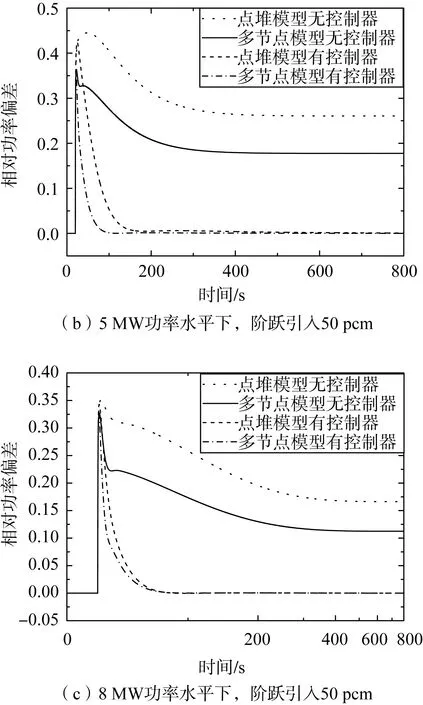
圖5 引入50 pcm反應性，堆芯功率PID控制響應曲線

在1 MW、5 MW、8 MW功率水平下，模擬堆芯系統在初始100 s內按初始穩態功率運行，在100 s時堆芯功率水平階躍至穩態初始功率的90%，然后穩定運行550 s后，在650 s時刻，堆芯功率水平階躍至穩態初始功率水平，點堆模型與多節點模型在PID控制器下的仿真結果如圖6所示。圖中可以看出，在PID控制器下，基于點堆模型、多節點模型計算得到的相對功率變化均與參考功率變化要求保持一致。可見，采用PID進行點堆模型和多節點模型下的堆芯功率階躍控制是可行的，且多節點模型比點堆模型控制效果更好。

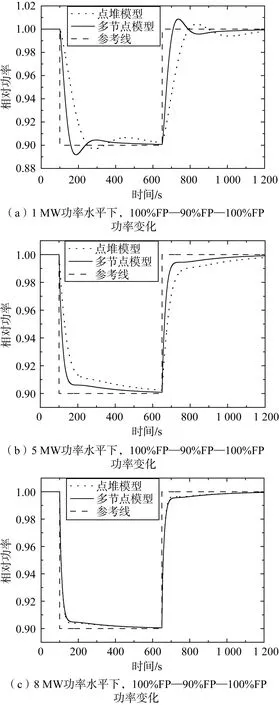
圖6 裝載233U燃料的堆芯功率PID控制響應曲線

4 結論

本文針對液態熔鹽堆堆芯功率控制問題，基于堆芯多節點模型和PID控制技術建立了堆芯功率控制系統。通過對比階躍反應性擾動下有、無控制器的仿真結果，證實基于堆芯多節點模型設計的堆芯功率控制系統可以實現堆芯功率調節與穩定。在堆芯負荷變化情況下，與基于堆芯點堆模型設計的功率控制器相比，基于堆芯多節點模型設計的功率控制器響應速度更快、超調量更小，實現堆芯功率穩定能力與功率調節能力更強。