高中數學解題技巧之“數”“形”結合策略

江蘇省通州高級中學 朱麗強

數形結合是高中數學中一個極其重要的思想和方法，學生認識和了解數形結合不僅有利于應試，也對培養邏輯思維能力有一定的幫助。在本篇文章中，我以平時的教學經歷舉例，針對數形結合的含義和作用做了簡單概述，并講述了數形結合在解題中的應用，旨在幫助學生了解到數形結合思想的重要性。

一、數形結合思想概述及意義

在數學中，數和形作為兩個古老的命題被人們研究至今，現在的人們對其有了新的定義——代數和幾何，并在這二者之下衍生了很多分支。看似是兩個截然不同的研究命題，一個講的是數的變化之美，一個追求的是形的自然之道。然而大道歸一，代數和幾何間其實有著很多的共通之處，二者是能夠相互轉換、相互印證的，這也是數形結合思想存在的基礎。一般籠統來講，數形結合指的是數和形之間有著一一對應的關系，具體可以表現在數軸上的每一個點都對應著一個實數。在中學數學的學習中，就是將抽象的數和具體的形聯系起來，化抽象為具體。

對于學生而言，數學是晦澀難懂的，最主要的原因就是其太過于抽象，無論是導數還是方程等都離日常生活太過遙遠，學生想不到自然就覺得很難。但若是運用數形結合的方法來解題，將數化為直觀的形表現出來，學生便可以迅速理解。比如圓的方程，寫作方程可能部分人并不能得出圓的性質，但是依照方程畫出圖形來，便可一眼看出圓的半徑、圓心等性質，這便是數形結合的妙用。巧用數形結合可以簡化解題思路，迅速在繽紛復雜的數和形中找到最優解，對于要應對高考的學子來說有著極其重要的意義和作用。

二、數形結合在解題中的應用

1.由數到形

實數和數軸的對應關系是由數到形思想最基礎的解答，后面學習的很多知識都是以數軸為基礎。初學實數時，可能部分學生對于這個概念并不是特別清楚，怎樣的數才能稱之為實數呢？書中給出了實數的范圍，它是由有理數和無理數組成的。但是看起來還是太過于抽象，直到我們引入了數軸這個概念，將每一個數都具體到數軸上，實數和數軸上的點一一對應，學生這才對實數有了直觀的了解。在概念的講解中，我們便應用到了數形結合的思想。而到了高中數學，對由數到形的變換有了更深層次的要求。

比如在求最值時，我便會給學生出題：“已知點A（4，1），B（0，4）和直線l：3x-y-1=0，試在l上找一點P，使|PA|-|PB|最大，求P坐標。”這道題要運用對稱性求解，將數化為“三角形兩邊之差小于第三邊”這一形的特征。首先設B的對稱點C，由BC中點在l上及BC垂直于l列方程組即可得到C點坐標為（3，3）。設AC與l交于點P，易得出P（2，5）。在l上任取一點D，由三角形兩邊之差小于第三邊列式，可得出P（2，5）即為所求。

2.由形到數

由形到數同樣是數形結合思想的一種具現形式，很多時候，幾何圖形是很難想象的，同學們在做這類題時也感覺十分麻煩。最簡單的，比如一個拋物線，開多大口，會和哪個軸相交，這都是問題，如果單單給出一個拋物線而沒有數字的輔助，自然是得不到這些信息的。但是如果運用數形結合的思想，將曲線數字化、方程化，我們通過研究方程來探究曲線的性質，而不是觀察圖形本身，一切都會變得簡單很多。由形化數，就是我們探究幾何圖形性質的一個工具。

以曲線為例，為了深入探究曲線的性質，我們將一個方程與其對應起來，一方面，曲線上的每一個點都是所對應方程的解，另一方面，方程所有解對應的點都在曲線上。曲線方程、軌跡方程等一系列將幾何具體到數上的問題統統可以用由形到數的思想解決。比如在講解軌跡方程時，我給學生出了一道題：“線段AB的端點B的坐標是（4，3），端點A在圓（x+1）2+y2=1 上運動，求AB中點M的軌跡。”這道題很顯然是一道軌跡方程題，我們應讓學生首先根據圓的方程寫出圓心、半徑，連接B點和圓心P，取PB中點N，由N、M分別是兩條線段中點得到幾個未知點的關系，最終可知M是一個圓的軌跡方程，利用定義求得。

3.數形轉換

很多復雜的問題不單單只是由數到形或是由形化數，更多的是需要學生將數和形結合起來，實現共同轉換，才能得到最終答案。數形轉換一般要求從題目的已知條件和要求的結論出發，從數到形，再由直觀的幾何圖形得到具體的數字，也就是正確的解。

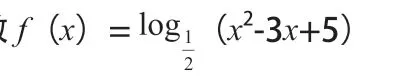
高中數學教學并不應只局限于教授知識，應更加側重于學生能力的培養。數形結合作為數學中極其重要的思想和解題方法，不僅讓解題變得更加方便快捷，更重要的是可以培養學生的邏輯思維能力。老師應該在平常方方面面的教學中對學生滲透數形結合的思想，為實現素質教育做出努力。