立式儲罐儲液晃動波面振動分析

周利劍, 許 田, 盧召紅,2*, 顧孝宋

(1.東北石油大學 土木建筑工程學院, 黑龍江 大慶 163318；2.中國石油管道科技研究中心中國石油天然氣集團公司油氣儲運重點實驗室，河北 廊坊 065000；3.中石油昆侖能源有限公司,安徽 合肥 230000)

隨著世界經濟的發展，各個國家對石油的依賴越來越大，立式儲罐作為石油化工重要的儲存容器，其在地震作用下的安全性至關重要，而在地震作用下過大的晃動波高是造成儲罐破壞的主要原因之一。立式儲罐的晃動研究始于二十世紀五六十年代，Housner[1]對儲液進行了質量簡化，將液體與罐壁部分同步運動的液體質量稱為“剛體質量”，相對罐壁晃動的液體部分稱為“對流質量”，并通過邊界元方法對兩質點力學模型進行了理論周期和波高的推導。其中的晃動周期公式被中、美、歐、日等國規范所采用；在Housner理論模型的基礎上，Abramson[2-5]等人對罐壁和儲液耦合又進行了深入研究，并推導出考慮彈性罐壁的理論波高公式。其中Harou-Housne的晃動波高公式被我國儲罐抗震規范[6-7]所采用。中國儲罐抗震規范的波高公式是在理論公式基礎上并應用于反應譜的形式給出的，其規范波高公式的計算只考量了一階晃動的參與，并沒有考慮多階振型的疊加，而且規范計算波高對實際工程設計波高的代表性有很大不確定性。因此，本文利用儲罐行業常用的有限元軟件ADINA對一萬方立式儲罐作地震作用下的晃動分析。通過不同地震動的輸入，來探究立式儲罐的晃動形態，并分析了激勵波高與儲液比及地震動峰值加速度的相關性，其結果對實際工程的波高設計具有一定的價值。

1 有限元模型的建立及地震波的選取

大型立式儲罐結構特點是容積大、罐壁薄、高徑比小，其在地震作用下結構響應包含許多非線性特征，例如儲液和罐壁耦合振動、罐底和基礎的相互作用以及儲液自身的非線性晃動等都表現出復雜的動力特性。特別是在大型立式儲罐試驗和規范計算中，因理論規范的假設和試驗振動臺對輸入地震動極限位移的限制，導致很難在不“失真”的情況下研究立式儲罐的晃動效應及形態。工程界對于這方面的研究方法有很多，其中有限元模擬是最為有效的方法之一。有限元軟件ADINA在液固耦合和非線性方面具有強大的計算能力，國內學者孫建剛等人[8]已證明ADINA對儲罐抗震計算的合理性。因此本文采用大型有限元軟件ADINA進行一萬方立式儲罐的晃動數值模擬，來探究晃動形態的特征以及晃動效應與地震動的關系。

1.1 有限元模型的建立

立式儲罐根據罐頂形式的不同分為穹頂罐和浮頂罐，大型立式儲罐為了安全性以及減少損耗常以浮頂罐的形式建造。而本文目的是研究儲罐晃動形態以及地震動頻譜特性和激勵波高的關系，因此采用敞口罐的形式進行有限元模型的建立。大型立式儲罐常采用填砂的環梁基礎進行浮放，本文為了便于運行模型并進行大量地震動激勵波高的研究，選擇采用實體基礎進行有限元模型的建立，基礎的幾何尺寸為直徑34 m、高度1 m；儲罐儲存介質用水來代替石油，從而更接近理論假設的理想流體的狀態；一萬方立式儲罐罐型參數為：罐高17.5 m、罐直徑28.3 m、儲液高度14 m，儲罐罐壁采用4節點殼單元，儲液采用等參8節點流體單元，罐底和基礎采用接觸單元，建立的有限元模型如圖1示。

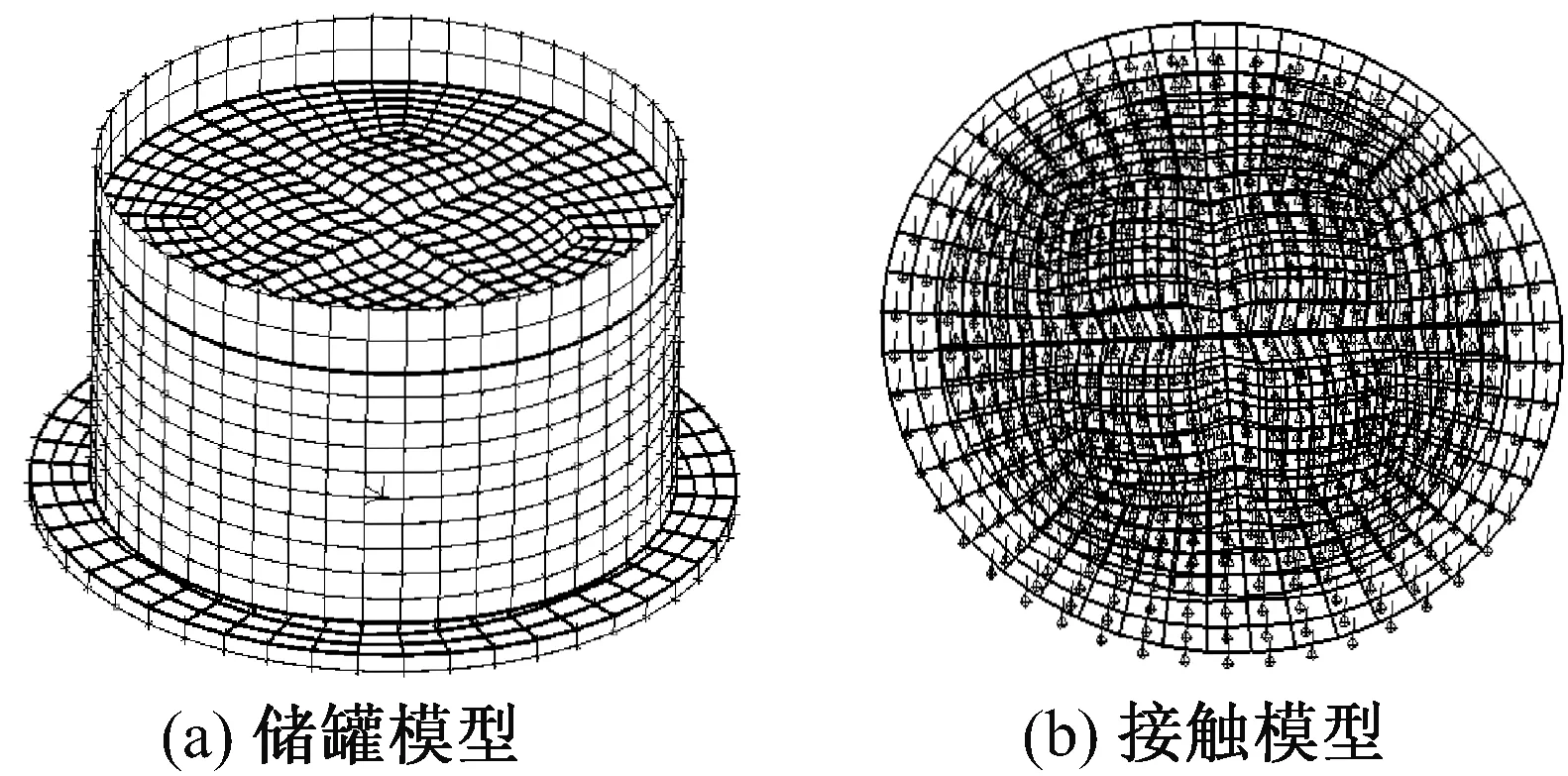
圖1 一萬方立式儲罐ADINA有限元模型Fig.1 ADINA Finite element model of 1×104 m3 vertical storage tank

1.2 地震波的選取

ADINA有限元軟件在使用勢流體模塊進行儲罐的地震動時程分析時，需要對儲罐以加速度的形式進行地震動輸入，也符合規范反應譜法以加速度譜進行地震響應計算的特性。儲罐屬于特殊設防類別的乙類結構，相關標準規定在進行儲罐抗震計算時應采用彈性時程分析進行地震作用下的補充計算。規范反應譜是大量地震動“統計意義”上的加速度擬合平均譜，不能完全反應真實地震動下的結構效應，也不能反應真實地震動下結構的“效應疊加”，特別是反應譜在長周期段的譜值擬合，存在較大爭議[9-15]。反應譜長周期段的譜值能不能有效地對長周期地震動響應進行設防，是工程界較為關心的問題，因此時程分析以小樣本容量的地震動響應計算來補充結構的抗震計算，這對結構的抗震設防尤為重要。GB 50011《建筑抗震設計規范》[16]中規定時程分析中地震波要依據地震動三要素進行選取，即有效峰值、持續時間和頻譜特性。

1.2.1 有效峰值

有效峰值即是圖2中的地震峰值加速度，也可用地震影響系數最大值amax除以動力放大系數βmax(一般取2.25)得到。我國的規范計算地震作用時常采用多遇地震進行彈性計算，同構造措施共同滿足中震設防的要求，所以在反應譜計算地震響應時運用多遇地震地面峰值加速度進行承載力計算。在時程分析補充計算時，對地震波峰值加速度以設防地震(中震)加速度進行賦值，地震波加速度調整方法如式(1)所示。

(1)

1.2.2 持續時間

一般情況下每條地震波的記錄時間都不同。規范規定選波持續時間為從開始到達最大峰值10%的點算起，到最后一次到達峰值10%的點為止；不論是實際強震記錄還是合成人工波，有效持時一般按照基本自振周期(5～10)倍，即控制結構頂點位移按基本周期往復(5～10)次；一般的地震波記錄持時都能滿足持時的要求，對于特長持時的地震波，工程中為加快計算速度，常對長持時地震波進行“抽點”處理，在不改變其頻譜特性前提下，盡可能反映真實地震動對結構激勵的動態響應。

1.2.3 頻譜特性

地震波的頻譜特性可用規范給出的地震影響系數曲線表征。設計加速度譜的制定是依據阻尼比0.05，并在大量地震動反應譜曲線擬合的基礎上得來的，因此選擇地震動的反應譜越接近規范譜，越能貼合規范對結構響應的計算；中國規范中絕對加速度反應譜，由地震影響系數曲線乘以重力加速度即可獲得，圖3為9度區、第一組的四類場地絕對加速度設計反應譜；我們選取本文所用地震波中的EL波、蘭州波、TCU052波和人工波進行反應譜生成，地震波峰值加速度取0.4 g，并與第三類場地設計譜進行對比，如圖4所示。從圖4可以看出，除了TCU052與反應譜擬合不協調，這也與TCU052為長周期地震動有關，其他三條地震動加速度譜與設計譜擬合就較為合理。

圖4 地震波反應譜和設計譜對比Fig.4 Comparison of seismic response spectrum and design spectrum

2 立式儲罐的晃動響應分析

2.1 地震動加速度峰值對晃動波高的影響

本節利用有限元軟件ADINA對一萬方立式儲罐作在不同峰值加速度地震動作用下的晃動響應分析，以探究大型立式儲罐波高和峰值加速度之間的關系。地震波選取了EL波、蘭州波、上海波、TCU052波和人工波，地震波加速度時程如圖5所示，每條地震波賦予0.05、0.1、0.2、0.3、0.4 g的地面峰值加速度，得到的晃動波高與加速度峰值如表1所示，并對五條地震波激勵波高做與加速度峰值的趨勢圖，如圖6所示。

由圖6可知，晃動波高隨烈度增加成線性增加。且在相同峰值加速度下，出現從蘭州波—EL波—上海波—人工波—TCU波增長的趨勢。從表1中可以看出峰值加速度由0.1～0.4 g變化過程中，蘭州波的波高變化范圍為226～651 mm，即峰值加速度每增加0.1 g，波高增加約為141.7 mm，波高隨加速度變化最為緩慢；而TCU波，峰值加速度由0.1～0.4 g變化過程中，波高變化范圍為1 517～6 381 mm，即峰值加速度每增加0.1 g，波高增加約為1 621.3 mm，波高隨加速度變化最為迅速。輸入地震動中TCU052的卓越周期為2.3 s，且含有豐富長周期成分，對儲罐的激勵波高最大，且激勵波高和峰值加速度的變化率也最大。其他四條中短周期波的激勵波高相對較小，且仿真中不同峰值加速度和激勵波高的關系較試驗更加線性化。為探究地震波相鄰峰值加速度對應波高的關系，我們對相鄰烈度的波高作比值，如表2所示。

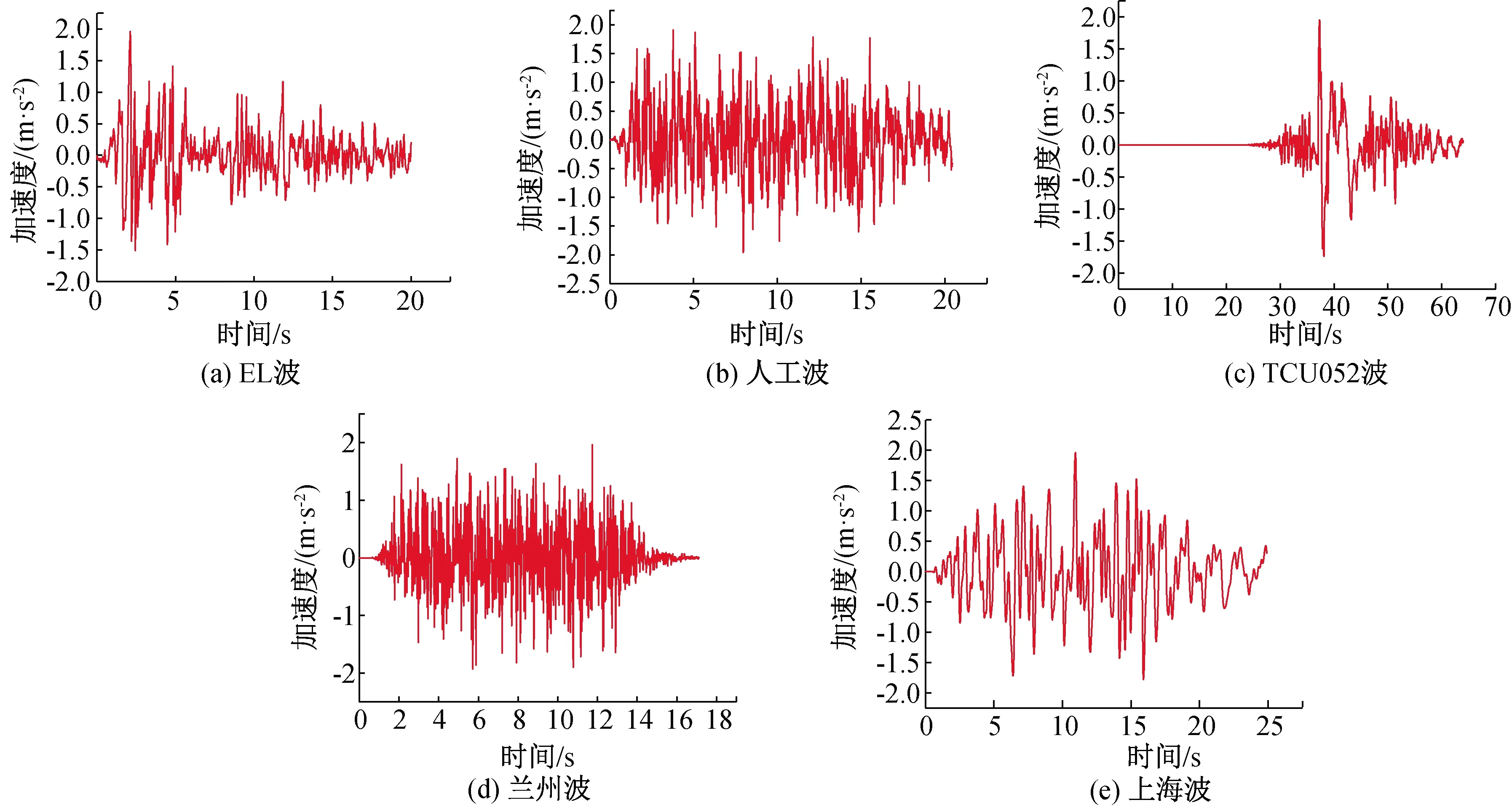
圖5 輸入地震波加速度時程曲線Fig.5 Acceleration time history curve of input seismic wave

表1 仿真波高 (單位：mm)

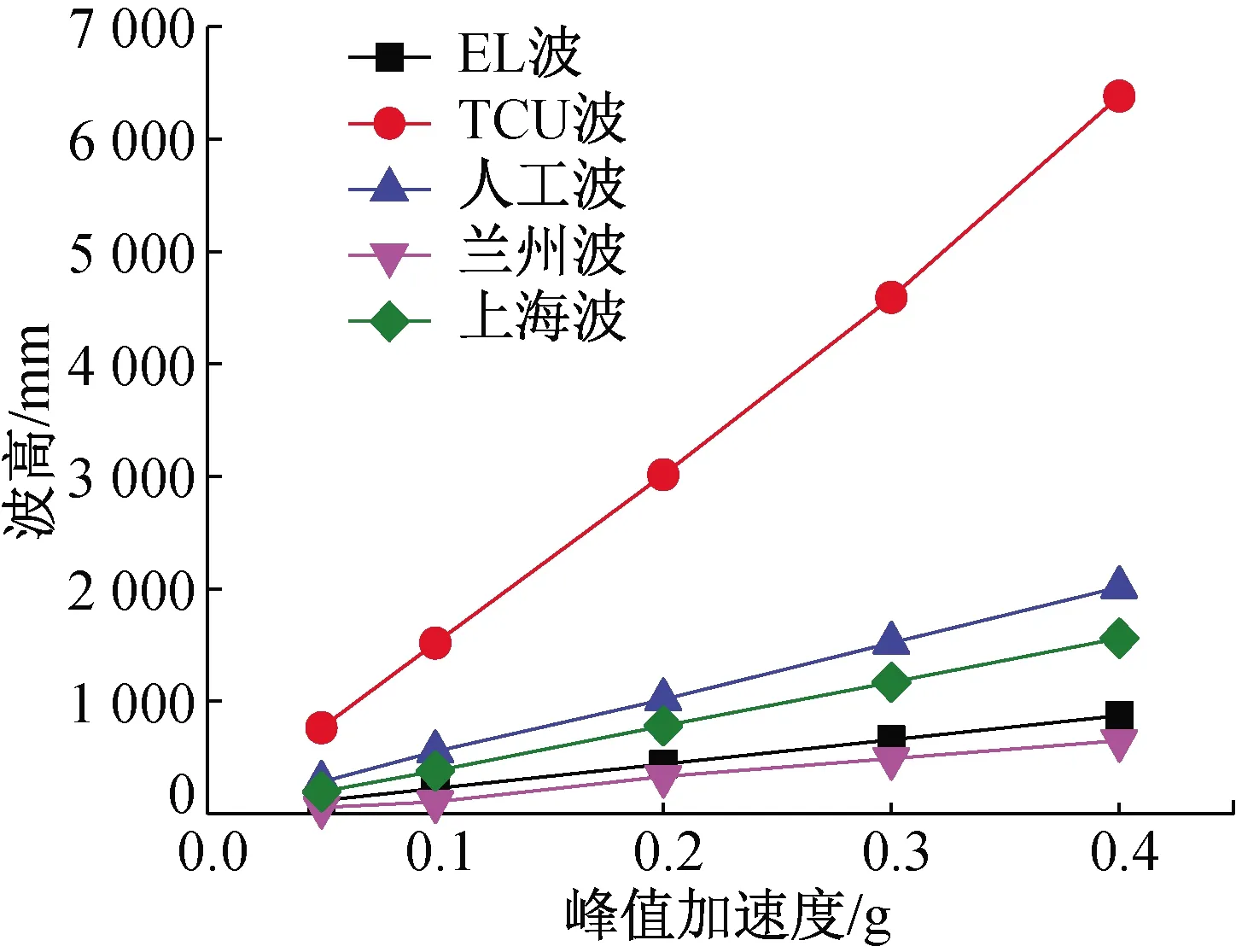
圖6 波高與峰值加速度趨勢關系圖Fig.6 Trend graph of wave height and peak acceleration

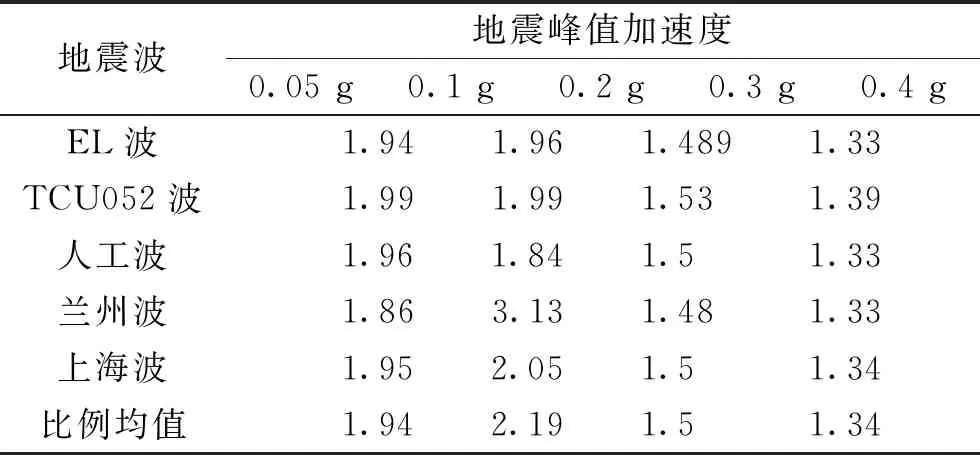
表2 相鄰峰值加速度激勵波高比值

注：比例均值=高峰值波高/低峰值波高。

由表2所示，五條地震波在不同加速度對應波高比值和兩加速度之間倍數近似相同。即加速度由0.05～0.1 g，0.1～0.2 g,加速度倍數為2，其對應的波高比值也接近于2倍；加速度由0.2～0.3 g, 加速度倍數為1.5,其對應波高比值也為1.5倍；加速度由0.3～0.4 g, 加速度倍數為1.33,其對應波高比值也為1.33倍。在中國儲罐規范中波高計算值和影響系數a成一定的關系，而影響系數又通過amax與地震烈度對應加速度成一定的線性關系，這種關系與仿真和試驗的關系一致。因此我們可以確定，地震作用下立式儲罐的晃動波高隨烈度變化而成線性變化，波高的比值和兩峰值加速度比值相等。

2.2 不同儲液比對晃動的影響

不同國家對立式儲罐液位到罐壁上沿的預留空間規定不同，預留空間的大小會影響儲罐的儲液比，那么不同儲液比對晃動是否有較大的影響仍然需要確定。在儲罐規范和理論研究中儲液比的考慮只體現在了晃動周期公式中，而波高公式中只通過晃動周期考量了儲液比。通過計算可知儲液比在規范波高計算中影響較小，而在實際地震中，儲液比對晃動的影響仍然需要探究。因此，本節利用有限元軟件對一萬方立式儲罐作不同儲液比下的晃動模擬，儲罐儲液比分別為60%、80%和100%，以觀察在接近真實地震環境下不同儲液比對晃動波高的影響。

輸入地震波選擇2.1節中的五條地震波，峰值加速度為0.2 g，有限元軟件對一萬方立式儲罐作模態分析和地震激勵下晃動仿真，提取的一階晃動周期和不同地震動激勵波高如表3所示。

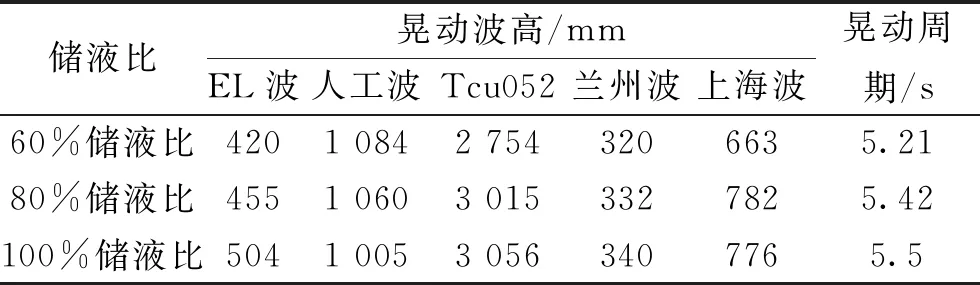
表3 不同儲液比的晃動波高和一階晃動周期

注：儲液比=儲液高度/儲罐高度。

由表3可知，隨著儲液比的增大，立式儲罐晃動波高變化并不明顯，晃動周期逐漸增大，但增長幅度較小，從儲罐晃動周期的理論公式中可知，儲液比對晃動周期的影響由tanh(Hw/D)來體現。通過對tanh(Hw/D)計算可知，儲液比的變化占公式計算結果的權重很小，因此從仿真和理論公式中可以得出儲液比對晃動周期影響微乎其微的結論；由不同儲液比對應的晃動波高值可知，儲液比對晃動的影響也較小，每條波對應的三個儲液比波高的比率保持在20%以下，平均最大比率為8%，因此儲液比的改變對儲液晃動波高和儲液自振周期的影響都很小，進而在后續的晃動研究中，我們只針對一種儲液比進行晃動研究。

2.3 立式儲罐儲液晃動波面振動分析

地震激勵下立式儲罐的晃動形態研究一直是晃動控制研究重要的內容，理論的波高簡化公式是假設儲液一階晃動，即認為罐壁處晃動波高最大，極值點以類簡諧波的形式，做波谷和波峰之間變幅度的往復運動。因此在真實地震動模擬下儲罐的晃動形態是否有高階參與，罐壁處波高是否最大等問題是大幅非線性晃動研究的重要課題。因試驗采集設備的限制，液面記錄只對特定點進行了時程觀測，而對全液面的觀測尚不能實現，因此本節借助有限元軟件ADINA進行波面振動分析，以探討地震作用下液面真實晃動形態。提取2.2節中0.2 g各地震動激勵下波面徑向各點的極值點波高，用于確定波面極值點位置，徑向各點極值波高如圖7所示。

由圖7可以看出不同地震動作用下液面極值點位置不同，5條徑向極值波高曲線中EL波和上海波的晃動最大極值點靠近液面中心，即在徑向位置15 m左右處達到最大值；蘭州波和人工波波高最大極值點在罐壁附近，即在徑向位置2.5～5 m和25～27.5 m之間達到最大值；TCU052波的波高極值點在罐壁處，即在0 m和30 m處達到最大值。因此我們可以知道儲液晃動是無規律的晃蕩，液面晃動極值點的位置也并非在理論假定的罐壁處。我們提取各罐壁處點的波高時程，并對波高時程做傅里葉變化，生成波高頻譜圖，如圖8所示。

由圖8可以看出，地震激勵下儲液晃動是無規律性的，液面晃動極值點越靠近罐壁處，罐壁處液面晃動時程曲線越光滑，這同時也說明一階振型參與度越大；從頻域中可以看出五個頻域卓越周期都接近一階晃動周期5.42 s，可以說明罐壁處液體晃動以一階晃動為主，但每個頻域圖主要的頻帶寬度不同，特別是液面晃動極值在液面中心位置的EL波和上海波最寬，其寬度約為2個卓越周期；其次是液面極值波高稍靠近罐心的人工波和蘭州波，其寬度約為1.5個卓越周期；頻段最小的是極值點在罐壁處的TCU052波，且頻帶寬度保持在一個卓越周期的頻域附近。因此可以說明儲罐晃動為多階振型的非線性晃動，液面晃動極值點越靠近液面中心，罐壁波高頻域寬度越寬，參與疊加振型越多。

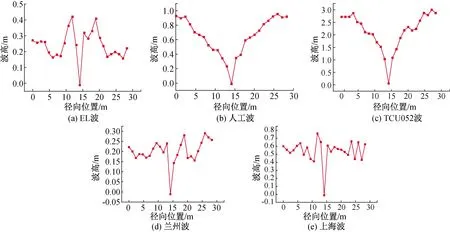
圖7 液面徑向各點極值波高Fig.7 Extreme wave height of radial points of liquid level

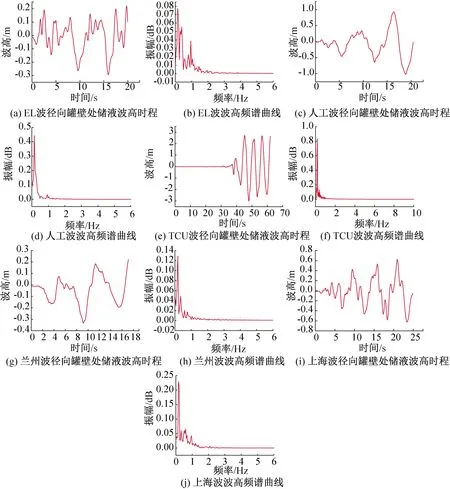
圖8 不同地震波激勵下罐壁處波高時域和頻域Fig.8 Time domain and frequency domain of wave height at tank wall under different seismic wave excitation

3 結論

1)立式儲罐在地震激勵下的波高與峰值加速度成線性增長，波高增長率約等于峰值加速度的比值，結論與規范、試驗相一致；立式儲罐的儲液比對晃動波高和晃動周期的影響較小，比較貼近理論公式中儲液比權重較小的結果。

2)提取一萬方立式儲罐在五條不同地震波激勵下的波高數據，不同地震波激勵下，儲液波面晃動極值點的位置不同，并非全如理論假設的在罐壁處；儲液的晃動是非線性晃動，極值點越靠近罐壁處，疊加振型越少，越靠近罐心處，晃動疊加振型越多，并且極值點在罐心附近的點，其儲液晃動形態明顯是由高階振型和一階振型疊加的結果。