一種通信信道優化迭代均衡的新型算法

余 蕾，黃 河

（96901部隊26分隊，北京，100085）

0 引 言

當前常規的迭代均衡算法，接收數據均衡后若譯碼結果錯誤，則需對譯碼結果重新進行編碼、調制、加擾，與訓練序列按照發送數據的幀結構組合，作為已知數據重新對接收數據進行信道估計，得到更加可靠的信道估計值，利用該信道估計值重新對接收數據進行均衡[1]。該算法利用第一次譯碼軟判決的糾錯增益，提高信道估計的性能，進而提高接收性能。本文先具體介紹當前迭代均衡算法思想及實施步驟，然后在原有算法基礎上進行優化并給出仿真結果。

1 迭代均衡算法介紹

1.1 數據結構介紹

本文中的迭代[3]均衡算法應用的數據結構為信息頭+N包數據，其中每一包數據中包含M個子幀，每個子幀由未知數據和已知數據組成，未知數據就是該數據包發送的原始信息比特經過編碼、調制、加擾后的符號，依次填入M個子幀中；信息頭包含TLC/AGC序列和同步頭等，由于本文只用到信息頭的信道估計結果，因此數據前面統一以信息頭代替。數據結構[2]如圖1所示。

迭代均衡算法主要思想是：利用第一次譯碼軟判決的糾錯增益，提高信道估計的性能。每包數據第一次譯碼錯誤后，將第一次譯碼結果重新編碼、調制、加擾，作為已知數據與接收數據再次進行信道估計，然后重新對當前數據包進行均衡譯碼。第一次譯碼雖然錯誤，但譯碼采用軟判決具有一定糾錯能力，較之前的硬判決會提高正確性。

1.2 均衡算法介紹

迭代均衡算法具體步驟如下。

第1步，若為第一包數據，利用信息頭進行RLS迭代計算得到的信道估計，若為第二包及后面的每一包數據，則利用前一包數據的最后一幀進行RLS迭代計算得到的信道估計，對第一幀數據進行均衡。

第2步，均衡后的數據進行RLS迭代得到新的信道估計，并對本幀數據尾部1/2數據重新進行均衡。

第3步，利用第2步得到的信道估計值對第2幀數據進行均衡，然后對第二幀數據重復步驟2。

第4步，從第3幀到本數據包最后一幀重復第2幀的過程。

第5步，M幀數據聯合譯碼。

第6步，若CRC校驗正確或CRC校驗錯誤但當前數據包的檢測次數達到2次，則當前包檢測結束，檢測下一包數據；否則，轉到步驟7。

圖1 數據結構

第7步，若CRC校驗錯誤，且本包數據檢測次數小于2，則利用本次譯碼的結果重新對本包數據進行檢測；第2次檢測時，在步驟4RLS迭代采用第一次檢測的譯碼結果作為已知數據進行迭代。

其中迭代次數通常為1次，多次迭代的效果不大，所以只取1次迭代的結果。

2 迭代均衡算法優化

本文針對原有的迭代均衡算法，從復雜度和性能兩個角度分別進行優化。

2.1 復雜度優化

由章節1.2迭代均衡算法流程可知，每個子幀數據均衡后，會進行判決，重新編碼調制，進行RLS信道估計，該信道估計值用于下一幀數據的均衡；原算法每個符號都會調用RLS模塊進行信道迭代。為降低復雜度，優化只利用每個子幀尾部的部分符號進行RLS迭代，可取子幀尾部的1/2或1/3或其他長度數據（長度要超過已知數據長度），即利用重新編碼后的未知數據尾部的部分符號和已知數據符號進行RLS迭代，原波形與新波形RLS迭代流程如圖2所示。

由章節1.2均衡迭代流程可知，當第一次檢測CRC錯誤時，會進行第二次檢測，第二次檢測RLS算法模塊以及RLS模塊的調用頻率一致，因此，新波形與原波形RLS算法復雜度總結如下。

數據包只檢測一次時：新波形RLS算法復雜度是原波形算法的1/n。

數據包檢測二次時：新波形RLS算法復雜度是原波形算法的2/n。

在降低復雜度的同時，算法的性能也略有所降。因此在實際情況中，可綜合信道情況以及性能要求考慮復雜度的降低，適當調整n值。

2.2 性能優化

原算法在第一次CRC校驗失敗后，利用第一次譯碼輸出的數據重新編碼、調制、加擾，更新迭代信道估計，即進行第二次迭代。由于每一個數據包分為M幀，后面M-1幀都是按照第一次迭代的譯碼輸出重新信道估計進行均衡，但第一幀還是按照上一數據包的信道估計進行均衡的（準確說是第一幀的前半幀，因為后半幀還會利用第一次譯碼輸出的數據結果進行RLS迭代得到新的信道估計重新進行均衡，即利用了第一次譯碼結果），即與第一次迭代采用的相同信道估計，相當于還是第一次迭代，并沒有利用上一幀第一次迭代的譯碼結果信道估計。針對第一幀的這種情況，在第二次迭代之前增加一個模塊：用緩存器保存上一數據包的信道譯碼結果以及上一數據包倒數第2幀末尾迭代信道估計值。若當前數據包CRC正確，則清除緩存器中上一包數據的譯碼數據，并將當前信道譯碼數據存入緩存器，再繼續處理下一數據包；若當前數據包CRC錯誤，需要二次迭代，則將保存的上一數據包倒數第2幀末尾迭代信道估計值作為初始值，用緩存器中上一數據包的信道譯碼結果重新進行編碼、調制、加擾，取最后一幀的數據（相當于本次第一幀的前一幀數據）重新迭代計算新的信道估計值。這樣，每一個數據包的第一幀數據就和后面幀的數據一樣進行了第二次迭代。注意第一個數據包的第一幀數據不需要做此操作，因為第一個數據包前面的信息頭是已知數據，因此不需要重復二次迭代。

優化算法流程如圖3所示。

圖4為修改算法與原算法區別示意圖。

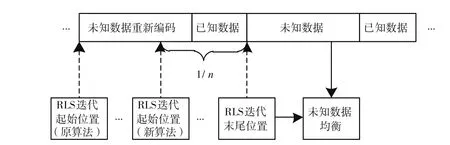
圖2 迭代均衡算法流程

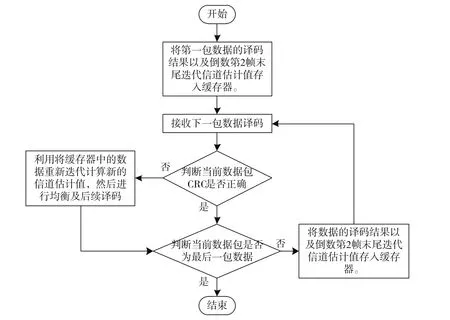
圖3 優化迭代均衡算法流程圖

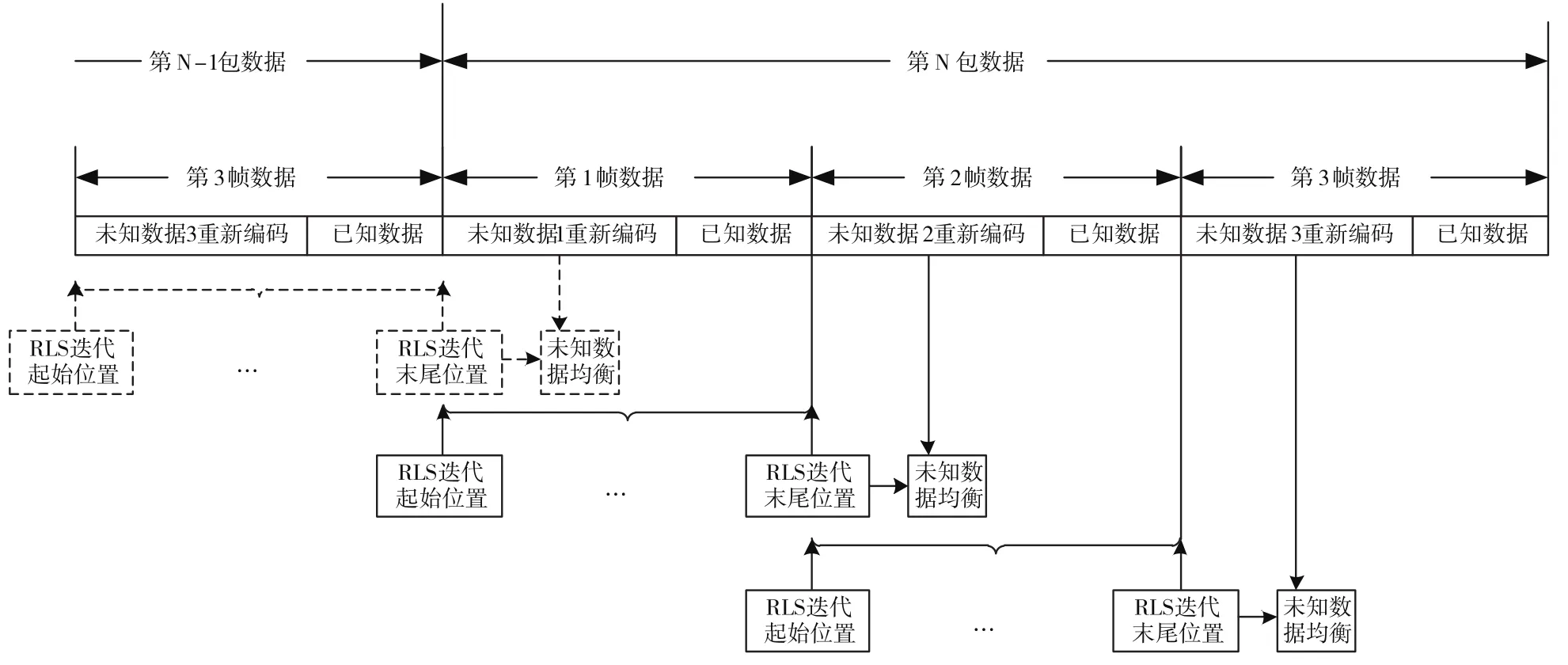
圖4 優化算法與原算法區別示意圖

圖4中，實線部分是原算法中的CRC迭代：每一包數據需要迭代時，第一幀數據實際上沒有進行迭代，而是重復第一次的均衡譯碼過程（因為其均衡使用的信道估計與第一次相同），后面的幾幀數據都是用本包中前一幀數據根據第一次譯碼結果重新進行信道估計迭代得到的新的信道估計進行均衡。虛線部分是修改算法后增加的模塊，即每一包數據需要迭代時，第一幀數據使用上一幀數據（即前一包數據的最后一幀）的譯碼結果重新進行信道估計迭代得到的新的信道估計進行均衡。

當一包數據中分為M幀時，修改后的算法復雜度為原算法的M/（M-1），即比原算法多了對一幀數據的信道估計迭代，還有一幀數據的編碼、調制和加擾，以及多了一個緩存器。但不是每一包數據都會增加復雜度，僅在第一次CRC校驗錯誤的數據包增加。

2.3 性能仿真

根據章節2.1和2.2的優化算法，本節將仿真以對比復雜度優化和性能優化后與原算法的性能對比。仿真信道：AWGN，數據包數：1 000。分別仿真了原算法（即圖中原算法-起始位置0）、原算法+降低復雜度（即圖中原算法-起始位置120）、新算法+降低復雜度（即圖中優化算法-起始位置120）的性能曲線，仿真結果如圖5所示。

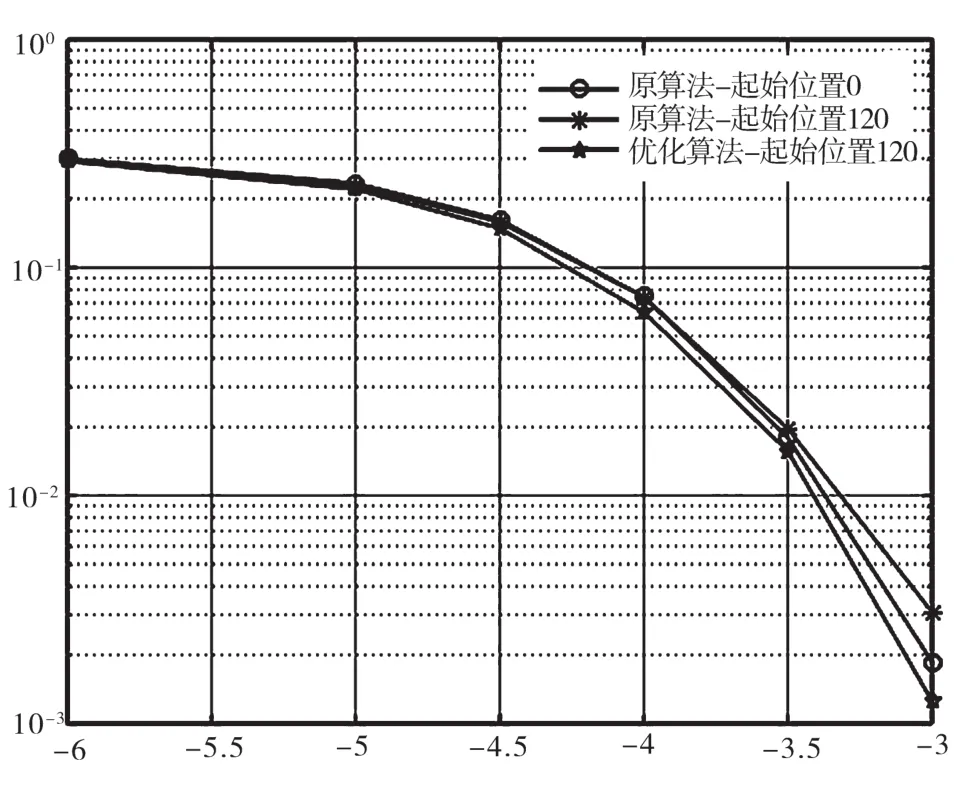
圖5 BER仿真曲線

根據仿真結果，對比原算法與原算法+降低復雜度可知，降低復雜度后性能下降并不多，與原算法基本相同。對比原算法+降低復雜度與優化算法+降低復雜度可知，優化算法性能略有提升，且在信噪比較高時提升更多。最后綜合對比優化算法+降低復雜度（優化算法-起始位置120）與原算法（原算法-起始位置0）相比，優化算法+降低復雜度整體性能更好。

因此，綜合兩種優化算法，可以同時使用降低復雜度和性能優化的算法，在降低復雜度的同時，性能還可以有提升。

3 結 論

本文在原有迭代均衡算法基礎上，提出了降低復雜度和優化性能兩種優化算法，具體改進如下。

（1）通過減少RLS迭代長度降低復雜度。

（2）通過更新每一個數據包第一幀（除第一包數據）第二次均衡時采用的信道估計值，即采用前一包數據最后一個子幀譯碼結果重新經過編碼、調制、加擾后再次進行的信道估計值進行第二次均衡，彌補了原算法對數據包第一子幀二次均衡仍采用第一次均衡時的信道估計值的漏洞。

仿真證明，降低復雜度對性能沒有明顯影響，而性能優化更適用于信噪比較好的情況。根據實際情況和對復雜度的要求，可以選擇合適參數使用文中兩種算法。