面向屬性網絡的可重疊多向譜社區檢測算法*
李青青,馬慧芳,2,吳玉澤,劉海姣
(1.西北師范大學計算機科學與工程學院,甘肅 蘭州 730070; 2.桂林電子科技大學廣西可信軟件重點實驗室,廣西 桂林 541004;3.甘肅農業大學管理學院,甘肅 蘭州 730070)
1 引言
在網絡分析中,社區檢測是最重要和最基本的任務之一,常被認為是圖聚類問題,應用于合著關系網絡和細分市場識別[1]等領域。在許多應用中,網絡中節點附有屬性信息(如合著關系網絡中作者的研究領域、發表論文篇數等信息),且節點可屬于多個社區(如合著關系網絡中作者致力于多個研究領域)。隨著網絡分析研究的深入,現已有大量有效的社區檢測技術被提出。然而多數社區檢測方法并沒有考慮節點的附帶屬性等信息,并且已有可重疊的社區檢測方法往往難以定位離群點。在針對屬性網絡的社區檢測方法中,譜算法[2]是流行的社區檢測算法之一,具有實現簡單的優勢且通常優于傳統的社區檢測算法。
傳統譜算法主要針對結構圖聚類,且節點隸屬于多個社區的信息被忽略,影響社區檢測的結果。近年來的譜算法對傳統譜算法進行了改進,可以歸納為以下兩方面:一是面向屬性網絡的不可重疊譜社區檢測方法,其主要思想是綜合考慮網絡拓撲結構和節點附著的屬性信息,使用歸一化拉普拉斯矩陣特征向量的譜算法。其中具有代表性的不可重疊社區檢測算法有,Jia等人[3]將屬性的重要性與信息熵相結合來選擇合適的屬性,并引入屬性約簡方法改進譜聚類,提出了NRSR-SC(Spectral Clustering based on Neighborhood Rough Sets Reduction)算法。Bonald等人[4]考慮網絡拓撲結構并結合屬性信息分配給節點的權值,量化了節點間的相對重要性,這種譜嵌入是基于適當的拉普拉斯變換的第一特征向量。盡管上述算法在效率和精度方面均有提升,但是隨著現實世界對網絡研究的深入,發現社區之間存在的自然重疊現象不容忽視。面向屬性網絡的可重疊社區檢測方法結合了網絡拓撲結構和節點屬性的相似度,綜合考量將信息映射成特征值與特征向量的方式。如Goyal等人[5]使用譜聚類算法解決社區檢測問題,設計了更快速的譜聚類近似算法。Li等人[6]針對網絡收斂特性,提出基于節點收斂度的重疊社區檢測算法SCNCD(Spectral Clustering based on Node Convergence Degree)。該算法同時考慮節點的局部和全局信息,利用改進的PageRank算法得到全局網絡中各節點的重要性,并結合局部網絡信息度量結構的收斂程度,通過譜聚類來識別重疊群落。盡管這類工作充分考慮了網絡中的信息并可用于可重疊的社區檢測任務中,但仍然無法基于譜算法檢測出網絡中的離群點,也無法控制重疊程度,且具有社區劃分數量限制的局限性。
針對以上問題,本文從網絡拓撲結構和屬性兩個角度出發,設計了面向屬性網絡的可重疊多向譜社區檢測算法OMSCD(Overlapping Multiway Spectral Community Detection)。該算法可將網絡劃分成任意數量的社區并有效發現離群點。首先,從結構和屬性兩方面綜合考慮,基于結合結構和屬性信息的計算加權模塊度設計了最大化到向量分區的節點映射方法;其次,考慮簇中心向量的初始選擇對于社區檢測結果的影響,給出簇中心向量的初始選擇策略,并將其融合在面向屬性網絡的重疊度和離群度制約中,實現具有離群點的可重疊社區的發現;再次,設計節點分配策略,將節點分配給與其簇中心向量具有最高內積的社區;最后,通過節點隸屬社區的情況,高效地在屬性網絡中檢測出內部結構緊密、外部連接稀疏、可重疊和具有離群點的社區。將本文算法應用于真實網絡中,實驗結果表明,即使是在社區規模不平衡的情況下,本文算法也具有較好的性能,從而驗證了本文算法的有效性和效率。
2 基礎知識
2.1 問題定義
給定屬性圖G=(V,E,F),其中V={vi}i=1,…,n表示圖中節點集合;E={(vi,vj)|vi,vj∈V}表示邊集且|E|=m。G的拓撲結構記作鄰接矩陣A,若(vi,vj)∈E,則Aij=1;否則Aij=0。F={f1,f2,…,fd}是圖中屬性的集合。fvi=[fvi1,fvi2,…,fvid]T是節點vi∈V的屬性向量。構建加權鄰接矩陣Aw,其元素定義如下:
(1)
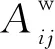
此外,為了描述清晰起見,本文涉及到的常用符號定義總結如表1所示。
2.2 加權模塊度
模塊度常被用來衡量社區劃分質量,對于無向無權圖,表示社區內的真實連邊與網絡在隨機放置下的期望連邊之間的差值。模塊度越大表示社區劃分質量越好。已有社區檢測方法中常常利用模塊度最大化思想來發現具有最高模塊度取值的網絡,從而捕獲網絡中的社區劃分。在面向屬性網絡的社區檢測中,將節點所攜帶的屬性向量化,以其屬性相似性值作為邊權重,綜合節點的屬性和結構信息。因此,用加權模塊度比用傳統模塊度度量社區劃分質量效果更佳。

Table 1 Commonly used notations definition表1 常用符號定義
定義1(加權模塊度) 給定Aw,加權模塊度計算所下所示:
(2)
其中,mw是Aw中邊的權重和值;cij是指示函數,如果節點vi和節點vj在同一個社區,則cij=1,否則cij=0。容易看出,加權模塊度中考慮了屬性權重信息。其取值越接近于1,社區結構越明顯,質量越好。
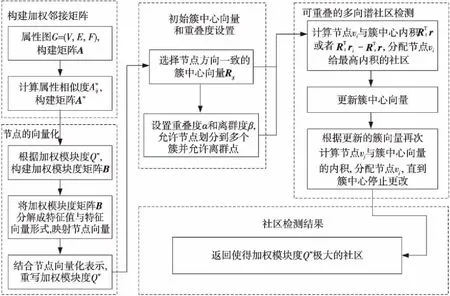
Figure 1 Framework of overlapping multiway spectral community detection algorithm圖1 可重疊多向譜社區檢測算法框架
現實網絡中存在自然重疊的現象,很多網絡中存在可重疊社區。例如,在社交網絡中,其中的每個節點對應于通常參與多個社區的個體。
定義2(可重疊社區) 圖中節點被劃為k個簇與離群點的集合C={C1,C2,…,Ck,Ck+1},其中Ci(i=1,2,…,k)表示特定社區,Ck+1是離群點集合。C1∪C2∪…∪Ck?C,且?Ci∩Cj≠?,即網絡中的某些節點不僅僅隸屬于單個社區,而是可同時屬于多個社區。
2.3 可重疊的多向譜社區發現算法基本框架
本文提出的算法流程如圖1所示,首先通過計算節點間的屬性相似性將值賦給節點間的邊,生成加權鄰接矩陣;其次,將生成的加權鄰接矩陣視為加權圖,應用加權模塊度來將加權模塊度矩陣分解成特征值與特征向量的表示形式,從而得到節點的向量化表示,并將其融入到加權模塊度中,重寫加權模塊度;再次,選擇初始簇中心向量,并設置重疊度與離群度制約;最后,將節點劃分到節點與其簇中心向量內積最大的社區,循環更新,得到使得加權模塊度極大的具有離群點的可重疊社區。
3 面向屬性網絡的可重疊多向譜社區檢測
3.1 節點映射
將節點屬性間的相關性轉化為節點間的邊權重信息,再將加權模塊度矩陣分解成特征值與特征向量的形式,得到了節點的向量化表示。根據定義1,可將加權模塊度矩陣分解[7,8]成如下形式:
加權模塊度矩陣為n×n的對稱矩陣B,其矩陣元素定義如下:
(3)
則式(2)中的Qw可改寫為:
(4)

(5)
由于B的對稱性,可將其改寫成特征值與特征向量的分解形式:
(6)
其中,λl是B的特征值;Uil是正交矩陣U的元素,正交矩陣U的列是特征值所對應的特征向量。不失一般性,將特征值遞減排序:λ1≥λ2≥…≥λn。
結合式(2)和式(6),重寫Qw為:
(7)
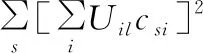
(8)
改寫式(8)如下:
(9)
根據加權模塊度的特征值與特征向量的近似,即將節點向量化表示,定義一組n個p維節點向量ri[9],向量ri中各值由式(10)計算得到:
(10)
改寫式(9)得:
(11)
其中,i∈s表示節點vi屬于簇s。
更具體地,n個p維節點向量ri在整個優化過程中是常數(因為ri是用加權模塊度矩陣的特征值與特征向量表示的)。然后,將網絡劃分成簇的加權模塊度(除了常數1/(2mw))的貢獻和,其中一個簇的貢獻等于該簇中節點的向量和的平方。社區發現的目標是最大化加權模塊度的劃分,該問題稱為最大和向量分割問題,簡稱向量分割問題。接下來,給出一種啟發式算法來快速解決向量分割問題。
3.2 簇中心向量的選擇
在面向屬性的可重疊的多向譜社區檢測算法中,將屬性數據作為網絡的輔助信息以增強網絡拓撲結構間的強度。通過將考慮了網絡拓撲結構和節點攜帶的外部屬性信息融入到加權模塊度公式中,得到了更精確的節點映射。通過每個節點的向量化表示,選擇k個社區的簇中心,以此來開展社區檢測任務。最簡單的k個簇中心的選擇策略是在n個節點中隨機選擇,但是這種策略具有較高的時間花銷。因此,本節設計了一種在屬性網絡中的可重疊多向譜算法的簇中心節點選擇策略。
考慮到在最簡單的情況下,選擇指向隨機方向且具有相同維度的簇中心向量即可。但是,由于網絡中存在社區結構,希望指向少數方向的多數節點向量被聚類,沒有或者很少的向量指向其他方向。并且選擇遠離集群方向的初始簇中心向量是沒意義的。因此,本文算法從節點向量中隨機選擇簇中心向量而不是選擇隨機方向的簇中心向量。這就保證如果大多數節點向量指向幾個方向,那么選擇也指向這些方向的初始簇中心向量。事實上只需要以這種方式選擇k個簇中心向量中的k-1個,最終向量將由簇中心向量總和為零來決定。
均勻向量l=(1,1,1,…)始終是加權模塊度矩陣的特征向量,這意味著所有其他特征向量的元素—即正交矩陣U的列必須總和為零(因為其必須正交于均勻向量)。根據式(10)有:
(12)
從而得到:
(13)
和
(14)
因此,一旦隨機選擇了k-1簇中心向量,第k個就可以利用式(14)計算。由于在初始化過程中存在一個隨機元素,所以在參數取值相同的相同網絡中,結果也不一定相同。因此,需在不同的初始條件下多次運行算法,選擇最高加權模塊度的社區劃分。
3.3 屬性網絡的重疊度和離群度制約
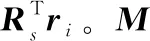
給定參數α與β,對于M使用參數α與β進行約束[11]:
(15)
3.4 可重疊的多向譜社區檢測
類似于k-means算法,OMSCD算法用向量代替點,向量內積代替距離。首先,選擇簇中心向量矩陣R中的一個簇Cs,將節點向量ri分配給與其距離最近的簇中心向量所在的簇,然后根據這些分配為每個簇計算新的簇中心向量并重復,新的簇中心向量為每個簇中節點向量的和,即:
(16)
可將式(11)改寫以最大化式(17)的目標函數:
(17)
當Qw與在上一輪計算的Qw相比值有所下降時,則認為上一輪使得Qw值極大的值為最好的劃分結果,即Qw達到收斂。社區檢測結果觀察加權模塊度的特性。假設將節點vi從一個社區Cs移動到另一個社區Ct,設Rs和Rt表示不包括節點vi的貢獻的2個社區的簇中心向量。然后,在移動之前,社區的簇中心向量是Rs+ri和Rt,移動后是Rs和Rt+ri。所有其他社區在此期間保持不變。因此,在移動節點vi時加權模塊度的變化△Qw是:
(18)

算法1OMSCD算法
Input:G=(V,E,F),社區數k,重疊度參數α,離群度參數β。
Output:指示矩陣M。
1:利用式(1)計算Aw;
2:利用式(3)計算B;
3:利用式(6)分解矩陣B,得到B的特征值與特征向量;
4:fori=1ton
5: 利用式(10)計算ri;
6:endfor
7:初始化簇中心矩陣R;
8:初始化指示矩陣M全為0;
9:while目標函數沒有收斂do
10:fori=1ton
11:forj=1tok
13:endfor
14:endfor
15: 初始化T=?,S=?,p=0;
16:whilep<(n+αn)do
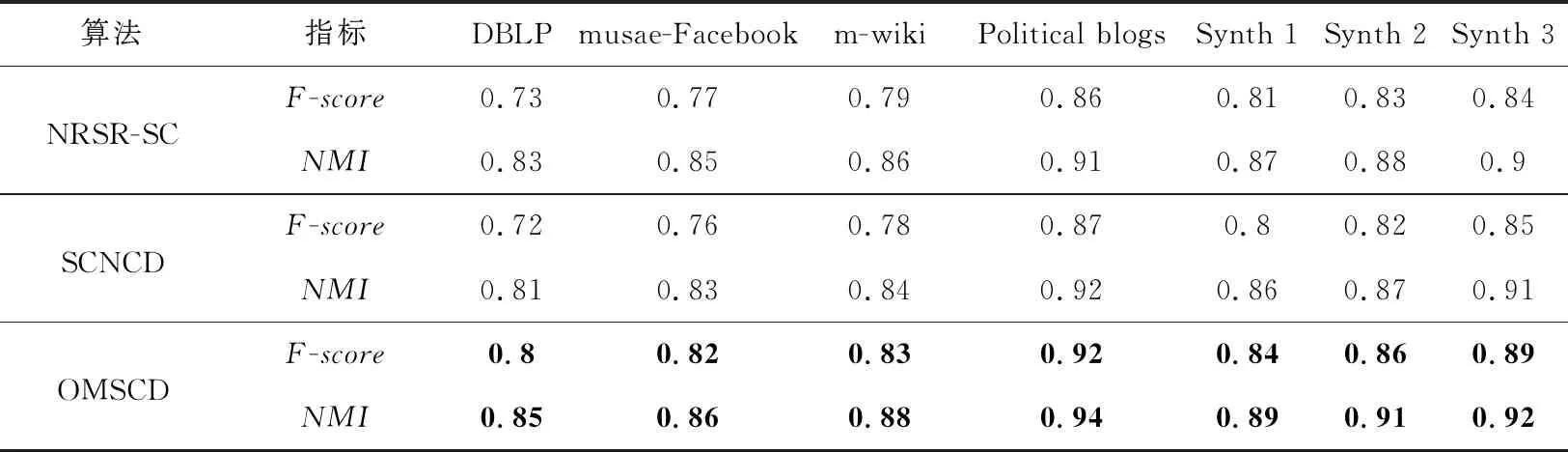
17:ifp 19:S=S∪{vi*}; 20:else 22:endif 23:T=T∪{(vi*,Cl*)}; 24:p=p+1; 25:endwhile 26: 根據式(16)更新簇中心矩陣R; 27: 計算節點向量ri與簇中心向量Rs的內積,更新矩陣O; 28: 根據式(17)計算目標函數; 29:endwhile 在算法1中,第1~3行根據公式計算Aw、B、B的特征值與特征向量;第4~6行得到節點的向量化表示;第7行依據3.2節初始化簇中心向量;第9~29行將圖中的每個節點分配到相應的社區中。第15行中T是存放節點vi屬于簇Cl的集合,集合中的元素為節點和相應簇的二元組;S存放被分配了的節點的集合;第17~20行用來判斷重疊度是否達到要求,若達到,將節點進行分配,否則停止分配;第26行更新簇中心向量;第28行計算目標函數,得到最好的社區檢測結果。 時間復雜度分析:在算法1第3,4行計算節點向量時,時間復雜度為O(n);將網絡劃分成k個可重疊的簇,計算節點向量ri與簇中心向量Rs的乘積oij,復雜度為O(nk);再根據oij對節點進行劃分時,時間復雜度為O((n+αn)×nk),由于α經常取較小的值,故時間復雜度為O(n2k);給定指示矩陣,更新簇中心矩陣的時間復雜度為O(nk);給定簇中心矩陣R,只需遍歷整個網絡一次來更新矩陣O,因此時間復雜度為O(nk)。設t為目標函數收斂所需時間,整個算法的時間復雜度為O(n+tn2k)。 為了驗證本文算法的有效性和效率,設計實驗進行驗證,實驗將回答以下幾個問題: 問題1OMSCD算法與現有在屬性網絡中的譜方法相比,性能方面存在哪些優勢? 問題2針對在面向屬性網絡的具有離群點的可重疊多向譜社區檢測任務,不同參數的設置是怎樣影響本文算法的? 問題3在真實的網絡中,實現社區檢測任務的效果如何? 4.1.1 人工數據集 使用LFR基準[12]生成允許節點隸屬于多個社區的屬性網絡。具體地,節點的度和社區規模大小分布分別由指數T1和T2控制。給定社區所需的節點數,通過分區約束將鄰接矩陣分成塊,為每一個塊選擇概率Pij,以衡量每個區塊之間的密度。對角線上的塊為實際社區,非對角線塊為社區間的交叉邊。另外,為節點分配屬性fi∈[0,1],屬性值需從正態分布N(μ,σ)中提取,其余的屬性從具有更大方差的正態分布N(0,1)中提取[13]。此外,為了檢測離群點與重疊社區,使該人工數據集至多具有βn個離群點,重疊度α的設置滿足0≤α≤(k-1)且α?(k-1)。其他參數設定為T1=2,T2=1,Pij=0.36,i≠j。表2給出了人工數據集的具體信息。 Table 2 Synthetic datasets表2 人工數據集 4.1.2 真實數據集 選取如表3所示的4個真實世界中可重疊的屬性網絡進行驗證。第1個數據集是DBLP(Digital Bibliography Library Project)的作者合著關系網絡。在該網絡中,節點表示作者,以作者間的合著關系為邊構建關系網絡,邊權重表示作者間的合作次數。musae-Facebook數據集是Facebook站點的頁面-頁面圖。節點代表官方的Facebook頁面,邊表示站點之間的相互喜歡,節點特征從站點描述中提取而來。第3個數據m-wiki來源于英文維基百科,代表特定主題的頁面-頁面網絡,其中節點表示文章,邊表示文章之間的相互鏈接。第4個數據集是美國Political blogs之間的定向超鏈接網絡,將節點間的有向邊視為無向邊驗證本文的算法。其節點表示博客,邊表示博客間的鏈接,政治傾向為屬性。真實數據集的具體信息由表3所示。 Table 3 Real datasets表3 真實數據集 社區檢測任務常使用F-score和NMI作為評價指標[14,15],定義如下: 定義2(F-score)F-score是召回率和精確率的調和平均: (19) 其中,Precision=|CT∩CF|/|CF|,Recall=|CT∩CF|/|CT|,CT表示真實社區,CF表示檢測到的社區。F-score值越大算法性能越好。 定義3(歸一化互信息NMI)NMI基于混淆矩陣N定義如下: (20) 其中,Nij表示屬于真實社區Ci和檢測到的社區Cj的節點的數量,Ni.是矩陣N中第i行中的元素構成的行向量,N.j對應于矩陣N中第j列元素構成的列向量。NMI度量了算法檢測結果與真實結果的相似性,相似性越高,NMI值越接近于1。 4.3.1 性能比較(問題1) 選取了NRSR-SC[3]、SCNCD[6]與本文算法分別從社區檢測的準確性和運行時間兩方面進行比較。其中NRSR-SC算法創新地提出采用約簡屬性來改進譜聚類進行不可重疊的社區檢測;SCNCD算法同時考慮節點的局部和全局信息通過譜聚類來識別重疊社區。因此,本文選取上述2種算法作為實驗參照。 表4顯示了在不同數據集上NRSR-SC、SCNCD算法與OMSCD算法結果的F-score和NMI的值。從表4中可以看到,NRSR-SC算法在較小的數據集上相比其他算法的性能較低,如Political blogs。這是由于屬性約簡方法降低了部分性能。SCNCD算法同時考慮了局部和全局的信息使其在較小的數據集上表現出了良好的性能,然而較多考慮局部信息使其在較大數據集上的性能有所降低。不論NRSR-SC算法還是SCNCD算法都對數據集的規模比較敏感,算法的F-score和NMI值受到了數據集規模的影響。而OMSCD算法由于選擇了與大多節點方向類似的簇中心向量,同時可檢測出重疊社區和離群點,不僅在不同規模的數據集上的性能表現較好,而且也具有較好的精度。 Figure 2 Comparison of algorithms runtime on different datasets圖2 不同數據集上算法運行時間對比 圖2給出了在4個真實數據集和3個人工數據集上的運行時間對比結果。隨著數據集規模的不同,3種算法的運行時間有所變化。其中OMSCD算法在各個數據集上都表現出了良好的性能,其運行時間是所有算法中最短的,比其他算法快6 s左右。一方面,這是源于本文算法節點映射時近似求解了對加權模塊度貢獻最大的特征值特征向量。另一方面,這是由于OMSCD算法簇中心向量的初始選擇,使其效率高于其他算法的。NRSR-SC算法和SCNCD算法的運行時間之所以長于本文算法的,是源于NRSR-SC算法屬性約簡過程占用了較多的時間,而SCNCD算法則是由于利用了節點收斂度等方法,使其在較大規模數據集上花費了較長時間。 4.3.2 參數研究(問題2) 分析OMSCD算法2個重要參數α與β,討論如何選擇α與β。現實中,一些聚類算法的模型參數設置不直觀,或者難以預測特定的參數設置的結果,但是OMSCD算法中的參數是直觀的,允許用戶自己設置。因此,用戶可以從自身的領域出發決定參數的設置。接下來將給出參數α與β對于本文算法的影響分析來估計參數α與β的設置。 Table 4 Comparison with other algorithms表4 與其他算法的比較 Figure 3 Influence of α on OMSCD algorithm on different datasets圖3 不同數據集上α對于OMSCD算法的影響 從圖4中可觀察到,隨著β值的增大,OMSCD算法的NMI值在逐漸下降。主要原因是較大的β會將原本隸屬于社區內的節點視為離群點進行處理,從而對社區檢測結果產生影響。在本文中,離群度參數β的設置是非窮舉的。接下來將給出運行本文算法進行社區檢測時離群度參數β的設置建議。在運行本文算法時,設zi表示節點vi與最接近的簇中心之間的距離。計算zi(i=1,…,n)的平均值(用μ表示)和標準差(用σ表示)。如果距離zi大于μ+3σ,則認為節點vi為異常點。也就是說,如果通過遵循統計中的3σ規則,節點到其最接近聚類的距離大于均值的3個標準差,則認為節點是異常點。這樣,就可以估計離群點的數值,從而得到β值。 Figure 4 Influence of β on OMSCD algorithm on different datasets圖4 不同數據集上β上對于OMSCD算法的影響 在本節中,設計一個案例分析來觀察所提出的OMSCD算法的性質。研究節點上所附著的屬性對于節點向量表示的作用,解釋4.3.1節所提到的簇中心向量的選擇對于社區檢測結果的影響以及是否可準確地檢測出離群點和可重疊社區,并觀測OMSCD算法的實用性。該案例將在美國的Political blogs網絡上進行,Political blogs網絡相對較小,可以直觀地顯示OMSCD算法的結果。 實驗結果如圖5所示,其中重疊度參數α=1,離群度參數β=0.007。利用OMSCD算法進行社區檢測任務。 Figure 5 Community detection results of OMSCD algorithm on the American Political blogs network圖5 OMSCD算法對美國Political blogs 網絡的社區檢測結果 從圖5可以看出,OMSCD算法將其分成了2個簇,矩形框中的節點、虛線橢圓區域中的節點分別表示政治傾向為正派和反派的信息。網絡中的重疊社區為實線橢圓框圈中區域,表示政治傾向為中立派。未圈中的節點是離群點,表示不參與任何派系。結果顯示,在屬性網絡Political blogs中,采用融合屬性信息和網絡拓撲結構的加權模塊度,通過加權模塊度最大化得到的節點向量有效地提高了社區檢測精度,并進一步證明了簇中心向量的初始選擇策略有助于提高算法的效率。此外,利用重疊度和離群度制約檢測出了可重疊社區以及網絡中存在的離群點。 本文針對現有譜算法受限于劃分數量且難以控制重疊程度的局限性,提出了面向屬性網絡的具有離群點的可重疊多向譜社區檢測算法。首先通過計算節點間的屬性相似性將值賦給節點間的邊,生成加權鄰接矩陣。同時,將屬性信息融入到加權模塊度中,利用考慮屬性信息的加權模塊度將節點映射到向量空間,通過設置重疊度和離群度,實現可重疊的多向譜社區檢測。在真實數據集上的實驗表明,本文算法在社區檢測任務中優于傳統的譜算法。
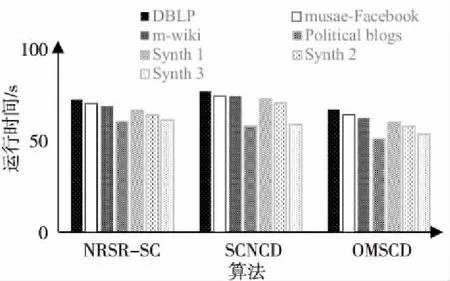
4 實驗與結果分析
4.1 實驗數據集描述

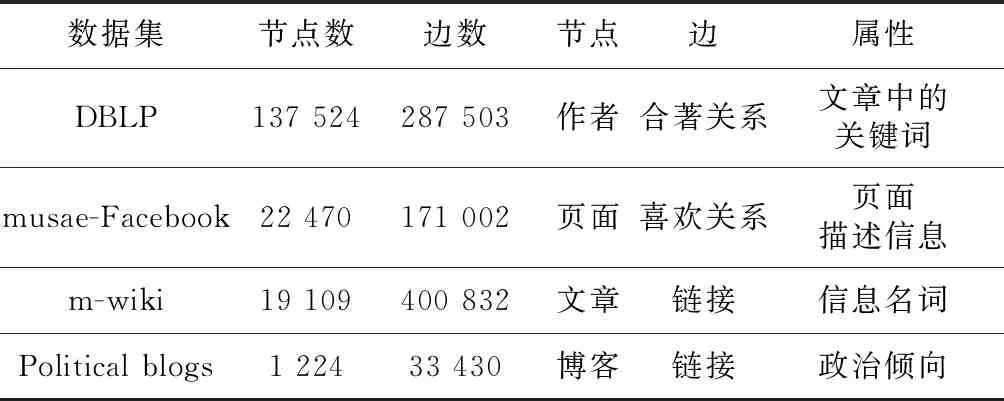
4.2 評價指標
4.3 實驗結果與分析



4.4 案例分析(問題3)

5 結束語

