鋼管樁碼頭地震易損性分析的單自由度模型*

高樹飛，馮云芬

(聊城大學建筑工程學院，山東 聊城 252000)

鋼管樁由于水平承載力高，而且彈性和韌性較好，在全直樁碼頭中得到廣泛應用。雖然鋼管樁碼頭的承載力和延性相比同等尺度的混凝土樁碼頭要高，但是在強震作用下仍會發生較大破壞。例如，1995年的日本Hyogoken-Nanbu地震造成神戶港Takahama碼頭的鋼管樁發生較大破壞，鋼管樁在樁帽和入土部分處均出現較大的彎曲變形，致使碼頭運行中斷[1]。因此，對鋼管樁碼頭進行合理的抗震設計和評估，對于港口的防災和減災具有十分重要的意義。傳統的高樁碼頭的抗震設計方法[2]，無論是基于力的方法，還是基于位移的方法，均是考慮確定性評估碼頭的抗震性能，無法考慮不確定性(包括地震動不確定性和結構不確定性)對碼頭抗震性能的影響，因此近年來從概率角度分析評估碼頭抗震性能正逐漸引起研究人員的關注，而地震易損性分析方法則是最常用的概率評估方法。該方法通過計算結構在不同地震動強度下發生不同破壞狀態的條件概率，從宏觀角度描述地震動強度對結構破壞的影響，其分析結果可應用于地震引起的災害損失評估和抗震加固改造決策，而這一條件概率即為結構易損性。

對于高樁碼頭的地震易損性研究，已有很多學者開展了研究，但基本上都是國外學者[3-7]開展的研究，國內目前只有馮云芬等[8]開展過相關研究，而且上述研究均針對混凝土樁碼頭。另外，在碼頭地震易損性分析中，通常須采用非線性動力時程分析方法對碼頭有限元模型進行分析，以確定碼頭在不同地震動強度下的地震反應值，再將反應值與碼頭結構的不同破壞狀態的定義值進行對比，則可得到結構在不同地震動強度水平下發生不同破壞狀態的概率，然后將破壞的概率擬合成易損性曲線[8]。由于碼頭結構的破壞狀態一般根據規范確定，因此合理準確地確定碼頭的地震反應值是易損性分析的關鍵。在上述研究中，對于碼頭的時程分析均是直接針對實際結構開展的，由于復雜的樁-土相互作用，且易損性分析須采用大量的地震波以考慮地震動的不確定性，故使得易損性分析的計算量非常大，不便于工程應用。目前，在工程結構的非線性時程分析中，為降低計算的復雜性，將原結構簡化為單自由度體系已是一種通行的做法，針對不同結構形式，已有學者提出了多種單自由度模型[9-11]，但尚未對鋼管樁碼頭易損性分析開展相關研究。

建立等效單自由度模型的關鍵是確立合理的恢復力模型，本文基于光滑型骨架曲線和Masing準則建立鋼管樁碼頭的恢復力模型，其中骨架曲線可由碼頭的推覆分析確定；為驗證本文提出的單自由度模型在碼頭地震易損性分析中的合理性和有效性，對一個鋼管樁碼頭案例進行易損性分析，比較原型結構和單自由度模型的易損性曲線的差異。

1 單自由度模型的構建

考慮到鋼管樁是鋼構件，而鋼構件本身并不具有負剛度特性，但由于P-Δ效應的影響，其骨架曲線也可能出現負剛度現象。考慮到碼頭的水平承載力主要由陸側樁提供(陸側樁的自由長度小)，通常可忽略P-Δ效應的影響，故本文不考慮骨架曲線的負剛度現象。結合文獻[10]和[12]對鋼管樁碼頭恢復力特性進行研究，本文采用式(1)描述的曲線型骨架線，見圖1。

(1)

式中：F為鋼管樁碼頭水平承載力；Δ為水平位移；Δ1和F1分別為首個樁塑性鉸形成時的上部結構水平位移和水平力；α和β為參數，可按表1確定。文獻[12]在確定α和β時考慮了樁-土相互作用。對于Δ1和F1，可通過對碼頭進行推覆分析予以確定。對于滯回規則，同樣參考文獻[10]和[12]，采用Masing準則。

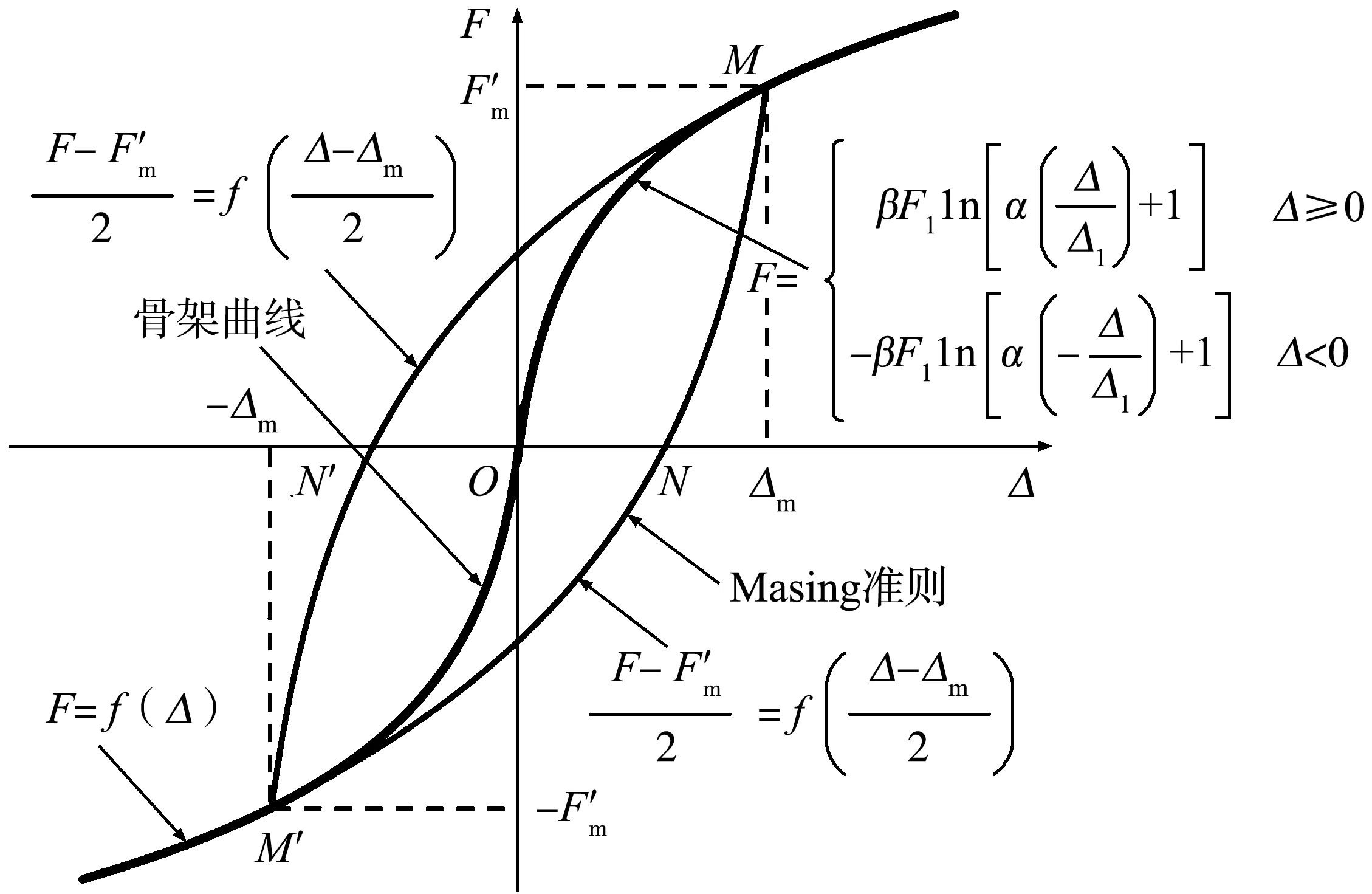
注：Δm為最大水平位移；Fm為最大水平位移對應的水平力。

圖1恢復力模型

表1 參數α和β的值

注:Su為黏土的不排水抗剪強度，對Su的中間值可通過線性插值予以確定α和β。

在確定好單自由度模型的恢復力模型后，對于單自由度模型的質量m，可以按照式(2)計算：

m=KT2/(4π2)

(2)

式中：K為碼頭彈性剛度，可取為碼頭Pushover曲線的原點到首個樁塑性鉸形成點連線的斜率；T為碼頭的自振周期，可對實際碼頭進行振型分析后確定，取為振型參與系數最大(碼頭橫向反應)的振型對應的周期。對于單自由度模型的阻尼比，一般參考規范[13]，取為5%。

2 易損性分析

參考文獻[8]，選用位移作為衡量碼頭抗震性能的指標，相應的易損性函數可用下式表示：

(3)

式中：C和D分別為鋼管樁碼頭的位移能力和位移需求；IM為地震動的強度參數；Φ(·)為標準正態分布函數；μD為鋼管樁碼頭在不同破壞極限狀態下的位移能力均值；μD為碼頭在相應的IM下的位移需求均值；βC和βD分別為碼頭位移能力和位移需求的對數標準差。另外，當位移能力μC是由Pushover分析確定時，βC的值可為0.3。

在確定碼頭易損性函數的方法中，云圖法的計算量較小，故本文考慮采用該方法確定碼頭易損性函數。采用云圖法確定碼頭位移需求的概率模型時，假定位移需求的概率分布為對數正態，且D和IM之間滿足以下的指數關系：

D(IM)=a(IM)bε

(4)

式中：a和b為參數，可通過回歸分析計算；ε為均值是1的對數正態隨機變量，同時其對數標準差為βD。對式(4)的等號兩側分別取對數可得：

我早已設計好，這次一定要雙手捧花，單膝跪地，紳士般求婚，“嫁給我吧。”然后擁抱，熱烈的吻，吻個死去活來。

ln[D(IM)]=lna+bln(IM)+lnε

(5)

(6)

(7)

式中：Di為第i次非線性時程分析得到的鋼管樁碼頭位移需求；n為計算中采用的地震波數目。由此，利用式(6)和(7)確定μD和βD后，將數值代入式(3)，則可得到鋼管樁碼頭的易損性函數。

對于鋼管樁碼頭的破壞極限狀態，本文考慮文獻[14]定義3個破壞狀態，分別為破壞狀態I-最小破壞、II-可控且可修復的破壞和III-可保障生命安全的破壞，并用鋼管樁的塑性鉸材料應變εs表示，見表2，其中地基深處樁塑性鉸是指塑性鉸所在位置的深度大于10倍樁徑。

表2 鋼管樁碼頭破壞狀態

3 案例分析

3.1 案例概述

鋼管樁碼頭斷面見圖2，排架間距為6.3 m，碼頭分段長度為47.1 m。鋼管樁直徑為800 mm，壁厚是10 mm，鋼材為Q345。岸坡土體為單一的砂土，其內摩擦角為30°。

圖2 鋼管樁碼頭斷面(高程：m；尺寸：mm)

3.2 地震波

地震波從美國太平洋地震工程研究中心的強震數據庫中選取，共50條。限于篇幅，地震波的相關信息從略。

3.3 易損性分析結果

采用SAP2000建立碼頭有限元數值分析模型，相關建模方法可參考文獻[12]。首先進行碼頭推覆分析，可得碼頭的荷載-變形曲線(Pushover曲線)，見圖3，圖中給出了首個鋼管樁塑性鉸出現時對應的位置，并給出了不同破壞狀態對應的位置。不同破壞狀態I、II和III下的μC分別為8.7、13.2、17.4 cm。

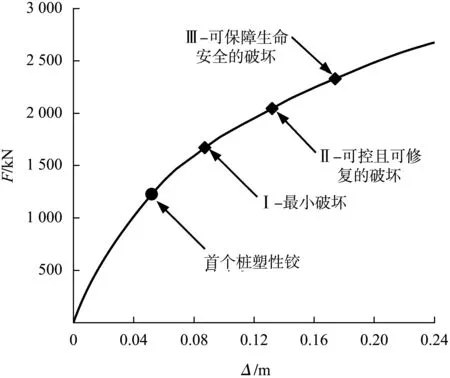
圖3 Pushover曲線

利用推覆分析得到的首個樁塑性鉸形成時的碼頭水平位移Δ1和水平力F1，可由式(1)確定等效單自由度模型的骨架曲線，再結合Masing準則和式(2)即可建立碼頭的單自由度模型。采用云圖法確定碼頭易損性時需要計算每一條地震波下實際碼頭和單自由度模型的位移需求，但是需要指出的是，本文中的單自由度模型只是用于確定碼頭的橫向位移反應，而計算碼頭總位移需求則需要考慮碼頭扭轉和雙向水平地震動的影響，本文采用文獻[14]的動力放大系數DMF來考慮這一影響，即在計算確定的碼頭橫向位移需求的基礎上乘以DMF，進而得到碼頭的總位移需求D。DMF的計算公式如下：

(8)

式中：e0為碼頭的初始偏心距；Ll是碼頭分段長度。對于本案例，經計算可得e0=6.40 m、Ll=47.1 m，代入式(8)后可得DMF=1.498。

通過非線性時程分析確定碼頭的總位移需求后，考慮地震動強度參數IM選用峰值地面加速度PGA，可得位移需求D和PGA之間的關系，見圖4，再根據式(6)和式(7)則可確定μD和βD。對于實際碼頭和對應的單自由度模型，μD可分別由式(9)和(10)計算，βD分別為0.371 5、0.341 5 cm。

lnμD=0.696 8ln(PGA)+3.081 8

(9)

lnμD=0.613 0ln(PGA)+2.992 8

(10)

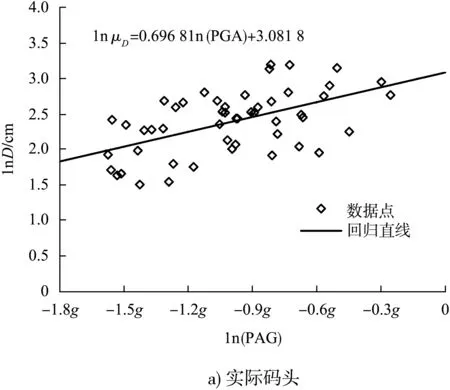
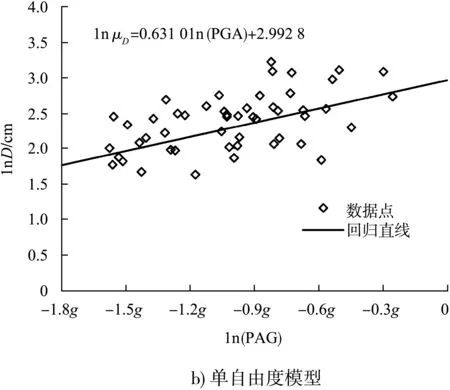
圖4 位移需求D的回歸分析

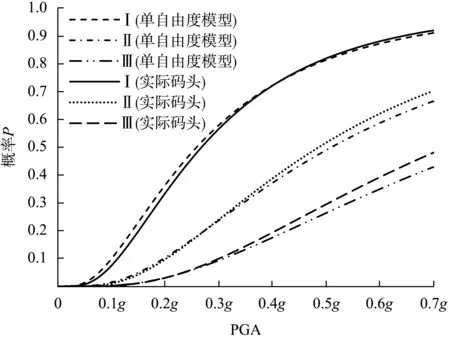
圖5 易損性曲線

將式(9)和(10)以及計算得到的βD代入式(3)，可得實際碼頭和單自由度模型的易損性函數，將函數用幾何圖形表示出來，即可得易損性曲線，見圖5。由圖5不難看出，隨著PGA的增大，碼頭結構發生破壞的概率逐漸增大，而且發生破壞狀態III的概率低于破壞狀態I和II，說明碼頭發生不可修復的破壞的概率較低；總體上實際碼頭和單自由度模型的易損性曲線相差不大，特別是在破壞狀態I的情況下；在峰值地面加速度PGA小于0.5g的情況下，二者的差別很小，但隨后二者的差距變大。考慮到二者易損性曲線的差別很小，因此在對實際鋼管樁碼頭進行易損性分析時，可以按本文的方法構建單自由度模型以代替原結構進行分析，以減小計算量和計算難度；另外，考慮到單自由度模型和實際碼頭易損性曲線在PGA大于0.5g的情況下有一定差別，故在此情況下的單自由度模型計算結果應慎重使用。

4 結論

1) 采用曲線型骨架線和Masing準則構建的單自由度模型可代替實際鋼管樁碼頭進行易損性分析，其易損性曲線與實際碼頭的曲線存在一定差別，但差別不大。

2) 采用單自由度模型進行鋼管樁碼頭易損性分析可以極大地降低計算量，但仍然無法避免進行大量的非線性時程分析，在下一步研究中可考慮對單自由度模型進行參數分析，研究易損性曲線和相關參數的關系，進而建立標準化的碼頭易損性曲線供碼頭抗震評估使用。