基于關聯性量化的碰撞安全性能正向設計

盧靜 鄭顥 歐陽俊 王玉超 鄧淯方

（廣州汽車集團股份有限公司汽車工程研究院，廣州 511434）

主題詞：正面碰撞 結構設計指標 乘員損傷指標 關聯性量化 正向設計

1 前言

轎車正面碰撞中的乘員保護設計包括車體結構設計和乘員約束系統設計兩部分。目前國內在乘員保護性能設計中先進行車體結構設計，再基于車體結構進行乘員約束系統設計，這種設計方法需要事先確定車體結構設計目標，而該目標的確定一般基于以往車型的開發經驗。當面向美國市場進行全新工況開發時，受開發經驗限制，沒有明確的車體結構設計目標，導致結構開發工作困難，存在反復修改車身結構并進行試驗驗證的問題。因此，如何建立美國標準開發工況下乘員損傷與車體結構之間可信的量化關聯性，根據乘員損傷開發目標制定車體結構設計目標，是美標項目碰撞安全性能開發的重點工作。

國外已有較多文獻基于正面碰撞工況研究了加速度波形與乘員損傷的關聯性，得到了較小的減速度峰值和較長的減速度持續時間有利于乘員保護[1-2]、增大動態壓潰和殘余變形可減輕乘員損傷[3]、理想的減速度波形是前端峰值較高、中間較低[4-5]等結論。國內研究也指出，提高第1階加速度峰值和降低第2階加速度峰值有利于降低乘員損傷指標[6-9]。上述研究從趨勢上分析了加速度波形與乘員損傷的關聯性，但沒有量化碰撞減速度波形與乘員損傷之間的關系，不能具體指導項目開發工作。

本文基于美國新車評價規程（US New Car Assessment Program，US-NCAP）全正面碰撞工況研究碰撞減速度波形與乘員損傷的量化關系，首先建立標準約束系統仿真模型，然后確定合理的車體結構設計指標和乘員損傷評價指標，最后基于標準模型分析不同車體結構設計指標下的乘員損傷指標變化規律，得到二者之間的量化關系，并基于得到的量化關系確定某車型USNCAP全正面碰撞工況下的車體結構設計目標。

2 車體結構設計指標與乘員損傷設計指標

2.1 車體結構設計指標

從波形變化趨勢來看，碰撞波形常見的簡化形式有等效方形波（Equivalent Square Wave，ESW）、尖頂等效方形波（Tipped Equivalent Square Wave，TESW）、等效雙梯形波（Equivalent Double-Trapezoid Wave，EDTW），如圖1 所示[10]。文獻[10]～文獻[13]研究表明，基于EDTW的胸部加速度與實際波形得到的胸部加速度十分接近。

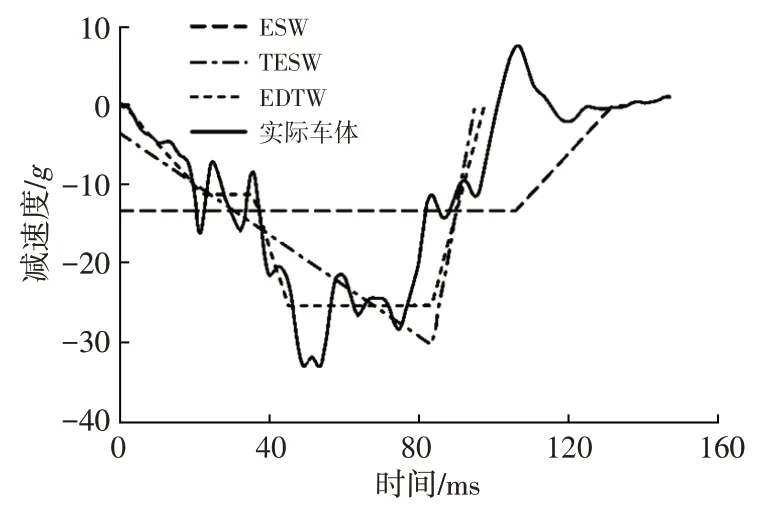
圖1 車體加速度擬合形式

對于正面100%剛性壁障碰撞，整車變形吸能區可以分為3個部分，即發動機前端與剛性壁障之間的結構變形D1、發動機后端與防火墻之間的結構變形D2a和防火墻的侵入變形D2b，如圖2所示。正面碰撞加速度-時間歷程可以分為3個主要階段：一階加速度G1（0～t2）、二階加速度G2（t2～t4）、G3（t4～t6），其中t2為發動機與壁障接觸時刻，t4為車輛開始反彈時刻。本文中，發動機懸置斷裂技術的應用使得發動機與壁障接觸后不會造成過大的加速度增加，二階加速度的增加主要由發動機與前圍接觸造成，故本文中t2設定為發動機與前圍接觸時刻。根據變形區域能量守恒原理，可以將實車碰撞波形簡化成物理特征明顯的兩階等效波形，包括發動機與前圍接觸前和接觸后2 個階段，如圖3 所示，其中G1為吸能空間變形波段（D1和D2a）的第1 階等效加速度，G2為D2b變形波段的第2階等效加速度。

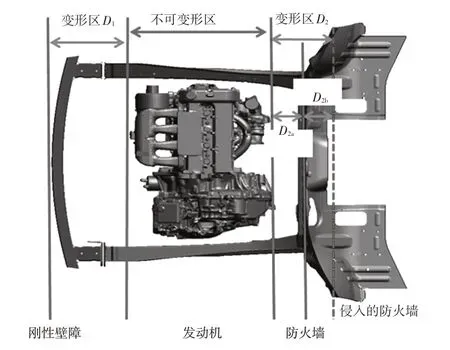
圖2 正面碰撞變形區

US-NCAP不考察胸部加速度，本文基于仿真分析模型采用頭部加速度、髖部加速度、左上肋骨壓縮量、右上肋骨壓縮量4個乘員損傷指標驗證了等效二階波形與實際波形的預測精度，結果如圖4～圖7所示。可以發現，4個乘員損傷指標一致性較高，簡化得到的等效二階波形可以較好地代表原波形。故選擇一階加速度G1、二階加速度G2、動態位移D作為結構設計的關鍵指標進行研究。

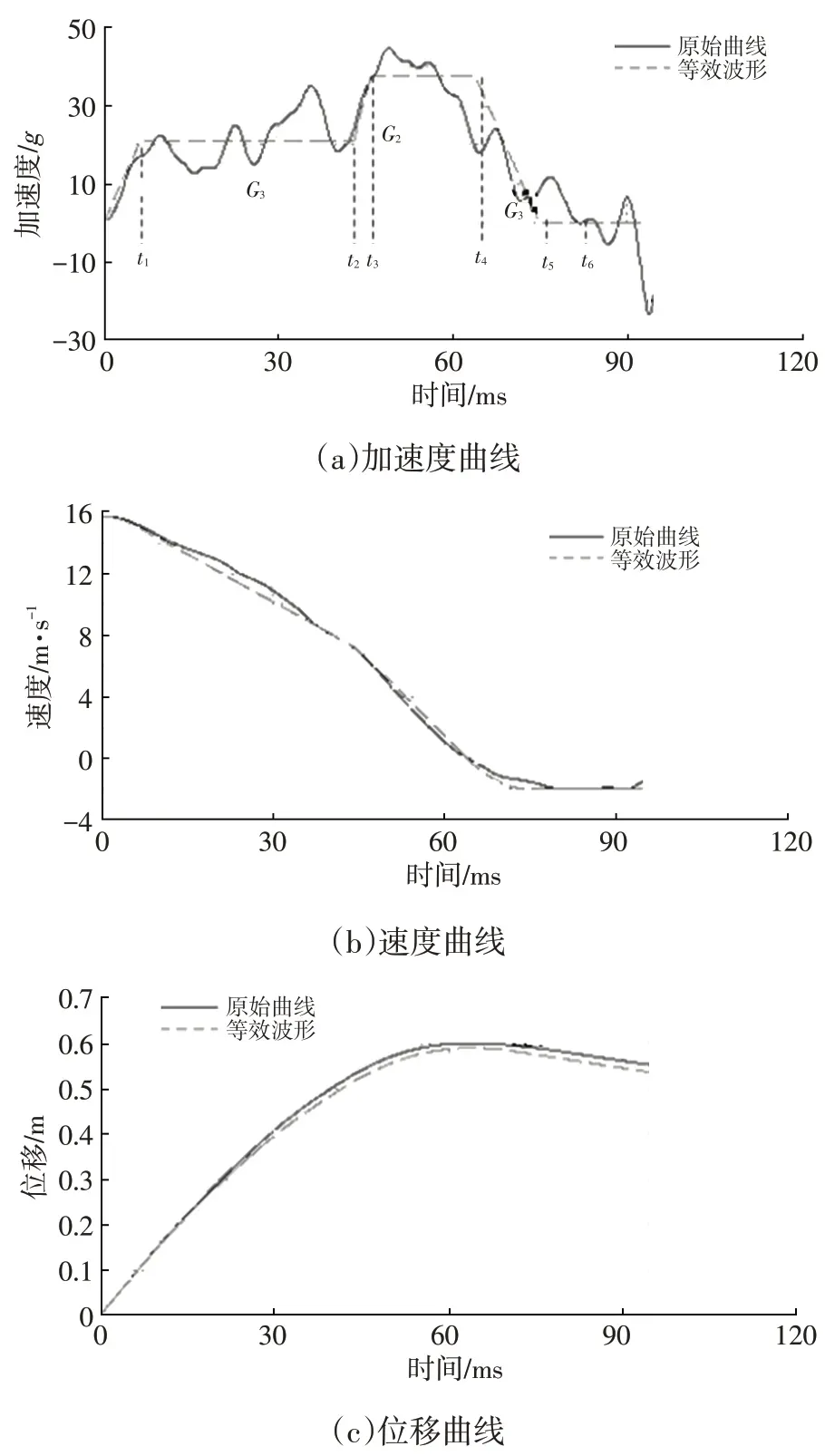
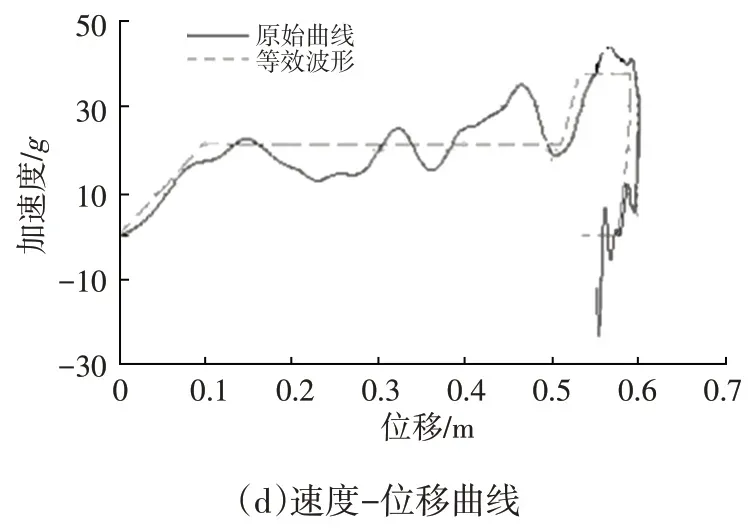
圖3 等效2階波形

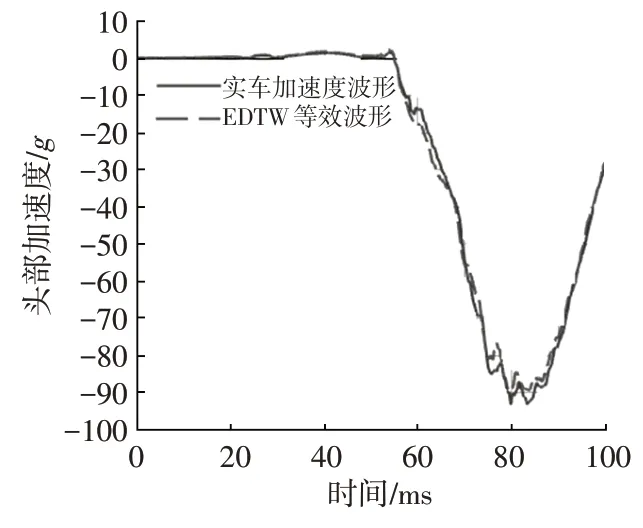
圖4 頭部加速度

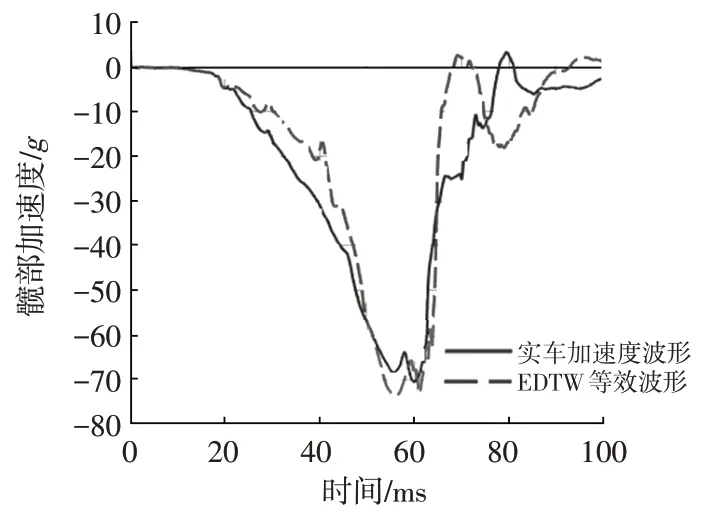
圖5 髖部加速度

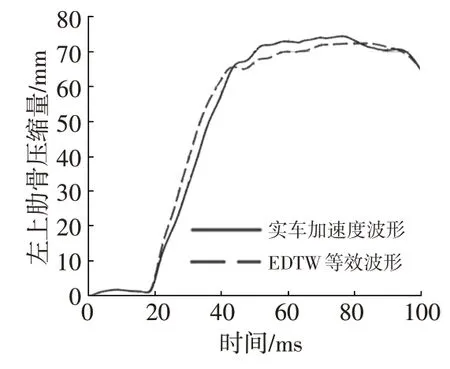
圖6 左上肋骨壓縮量

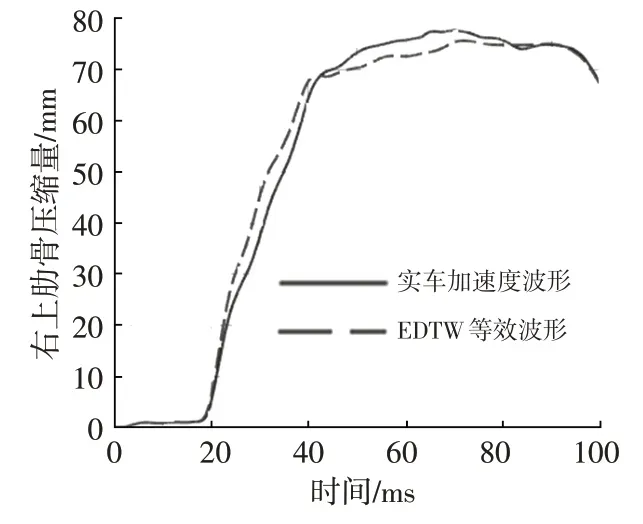
圖7 右上肋骨壓縮量

2.2 乘員損傷設計指標

US-NCAP計劃在未來的評價體系中采用一種新的考察假人——THOR假人，為應對未來版本的US-NCAP，本文選擇THOR-M假人進行研究，其考核指標如表1所示，其中車型1～車型7 為美國市場常見車型，包括雪佛蘭、日產、本田、豐田、福特等品牌。由表1可知，胸部壓縮量是該工況下失分最多的指標。同時，根據實際項目開發經驗，乘員左上肋骨和右上肋骨更容易受到安全氣囊的擠壓，故本文選擇THOR-M 假人左上肋骨和右上肋骨胸部壓縮量作為乘員損傷研究關鍵指標進行研究。

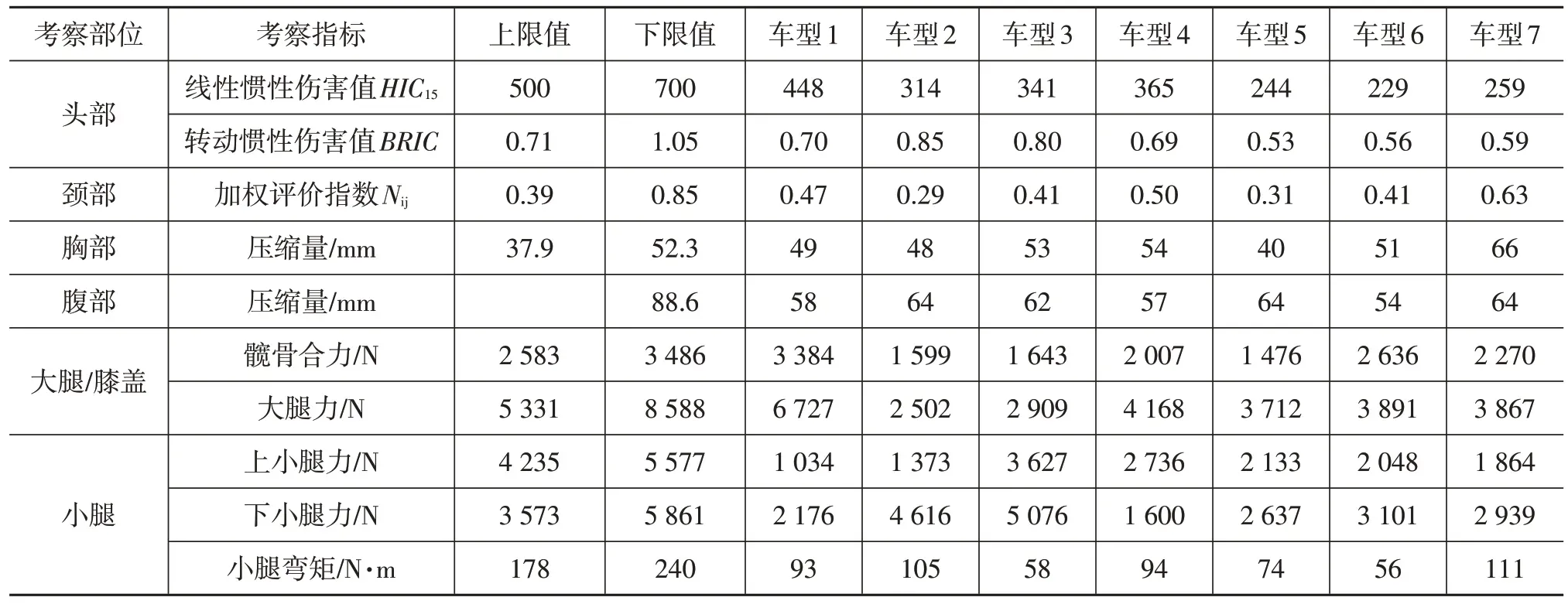
表1 US-NCAP未來版征求意見稿THOR-M假人評價規則

3 基于標準約束系統的乘員損傷優化流程

為了更直接地研究車體結構設計指標與乘員損傷之間的量化關系，提出了標準約束系統的概念，即固化較優約束系統配置。基于固化的約束系統配置對結構設計指標進行優化設計，然后基于較優的結構波形開展約束系統參數的詳細優化，新型優化流程如圖8所示。

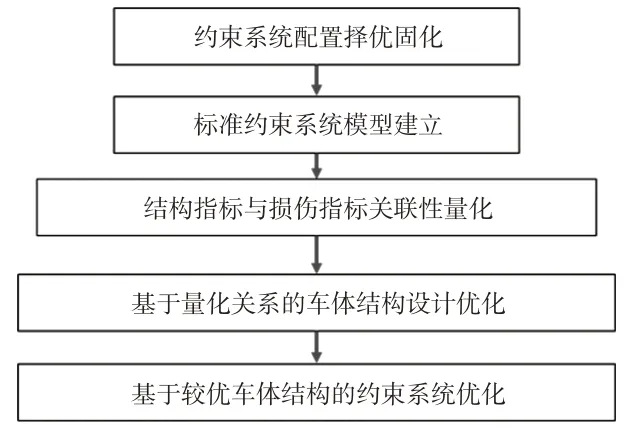
圖8 基于標準約束系統的乘員損傷優化流程

基于新型優化流程，首先對原型車約束系統配置進行固化，如表2 所示，然后開展基于約束系統固化配置的原型車56FRB工況碰撞試驗，并獲得加速度波形，如圖9 所示。然后基于原型車加速度波形建立有限元約束系統模型，如圖10所示，有限元約束系統模型對比結果如圖11所示，其精度達到85%以上，表明有限元模型可較好地反映原型車的損傷情況，建立的模型可用于后續分析。

表2 較優的標準約束系統配置

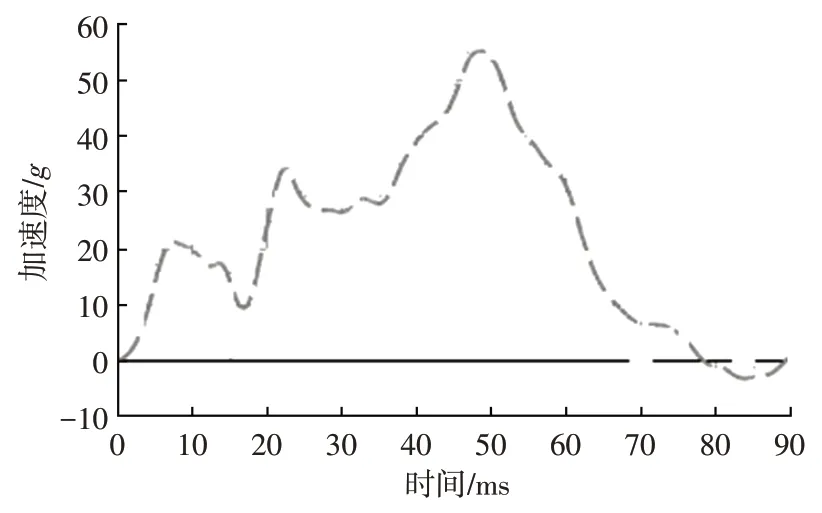
圖9 原型車碰撞波形

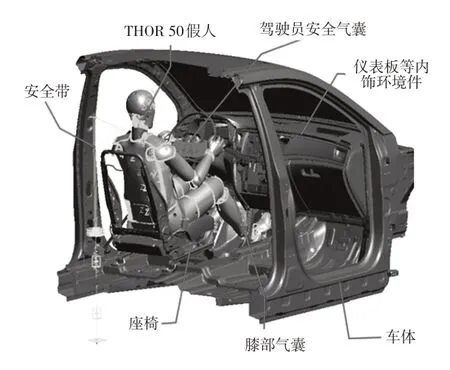
圖10 原型車仿真模型

4 結構指標對損傷指標的影響規律

將實車碰撞波形簡化成2階等效波形后，可以方便地研究波形典型特征對乘員損傷的影響，從而制定合理的結構指標。根據2.1節所述，將車體結構指標分為車體加速度（包括一階加速度G1、二階加速度G2）和動態位移（表征整車變形量，包括吸能空間和侵入量）。根據能量守恒原則：在動態位移D不變的情況下，改變G1時，G2會相應變化；G1不變的情況下，改變侵入量D2，G2會相應變化。故本文結構研究指標簡化為2種情況：侵入量D2不變，改變G1；G1不變，改變侵入量D2。

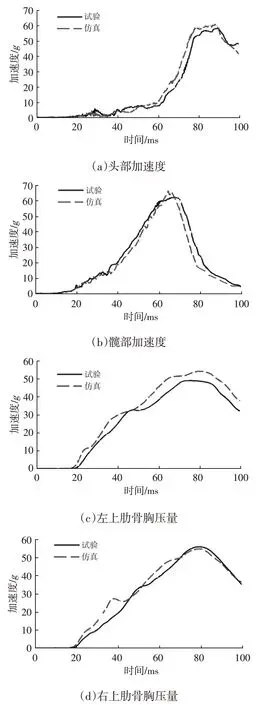
圖11 有限元約束系統模型仿真結果與試驗結果

4.1 一階加速度G1與乘員損傷的量化關系

根據2.1 中等效二階波形的轉換方法，在侵入量不變的情況下，通過改變G1得到10 組加速度波形，即波形1～波形10，如圖12 和表3 所示。等效波形轉換后，最大動態位移沒有發生改變，隨著G1的增加，G2不同幅度降低。

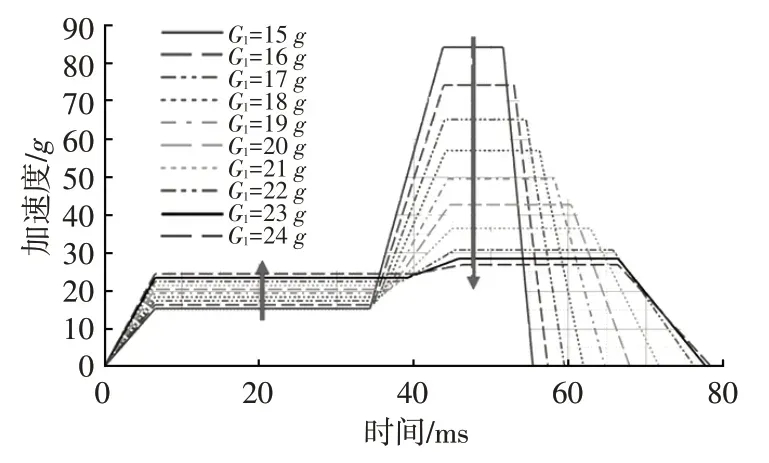
圖12 不同G1下等效波形

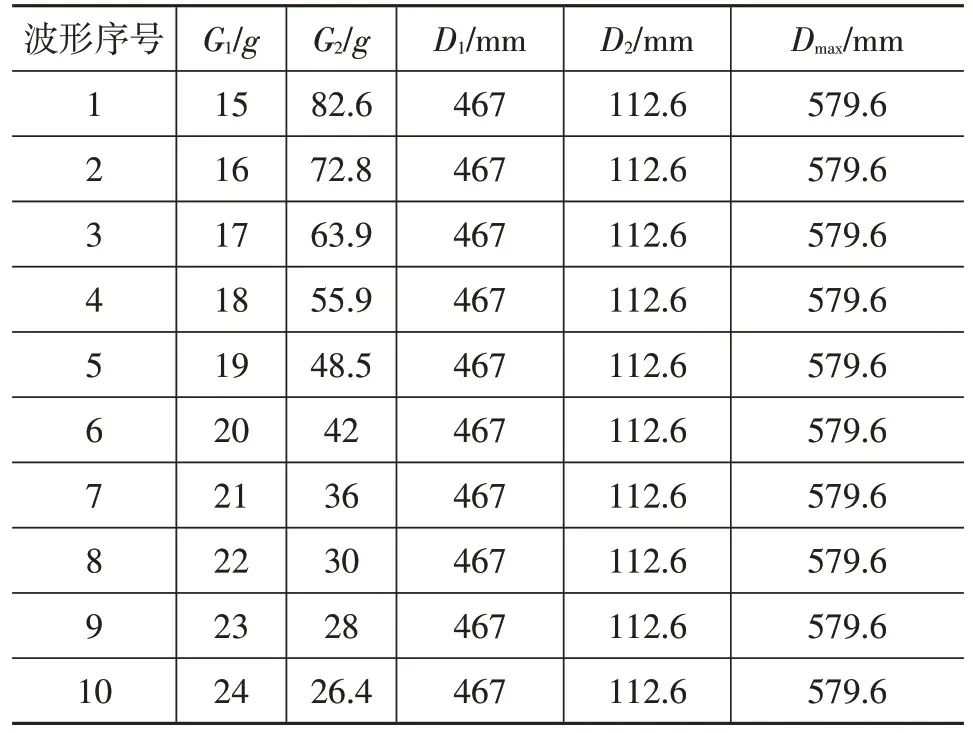
表3 不同G1下等效波形參數

基于前文的標準有限元約束系統模型，對10 組等效波形進行仿真計算，得到不同等效波形與損傷指標的關系如圖13、圖14 所示，可以發現：第38 ms 前，僅在安全帶作用下，胸部壓縮量隨著G1的提高而增加；第38 ms 起，氣囊與胸部接觸，胸部壓縮量開始降低，隨后，在安全帶和安全氣囊的綜合作用下，胸部壓縮量隨G1的提高呈現降低的趨勢；在第63～70 ms，轉向管柱完成潰縮，胸部壓縮量呈現降低趨勢。對胸部壓縮量變化的原因進行分析可知，其變化主要可以分為3 個階段：初始時刻到氣囊與胸部接觸時（階段1）；氣囊與胸部接觸時到轉向管柱開始潰縮（階段2）；轉向管柱潰縮時到碰撞結束（階段3）。階段1 直接受G1影響，約束系統影響因素單一；階段2 直接受G2影響，約束系統影響因素單一；階段3 車體開始反彈，轉向管柱開始潰縮，約束系統影響因素復雜。故階段2 胸部壓縮量變化情況是車體加速度的最直接反映。從圖13 可以發現，第63 ms 時刻，左上肋骨胸部壓縮量變化規律明顯，當G1≤22g時，其對胸部壓縮量影響顯著，G1每增加1g，左上肋骨胸部壓縮量降低約2 mm，當G1＞22g時，其對胸部壓縮量影響較小。

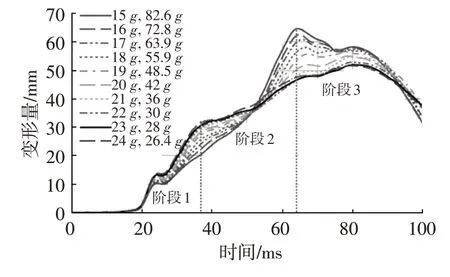
圖13 左上胸部壓縮量

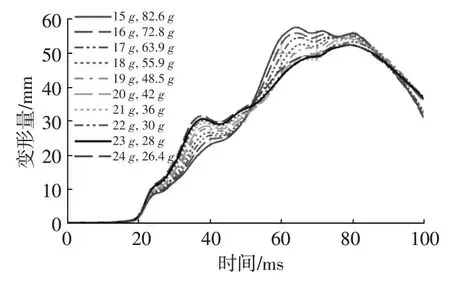
圖14 右上胸部壓縮量

按照上述方法對第64 ms 時刻右上肋骨胸部壓縮量進行分析，結果與G1對左上肋骨胸部壓縮量的影響相同。故G1較優值設定為22g。

4.2 侵入量D2與乘員損傷的量化關系

根據2.1 節中等效2 階波形的轉換方法，在G1不變的情況下，通過改變D2，得到5 組加速度波形，即波形11～波形15，如圖15 和表4 所示。等效波形轉換后，G1沒有發生改變，隨著D2的增加，G2不同幅度降低。

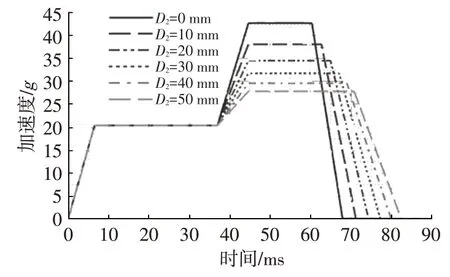
圖15 不同侵入量D2下的等效波形

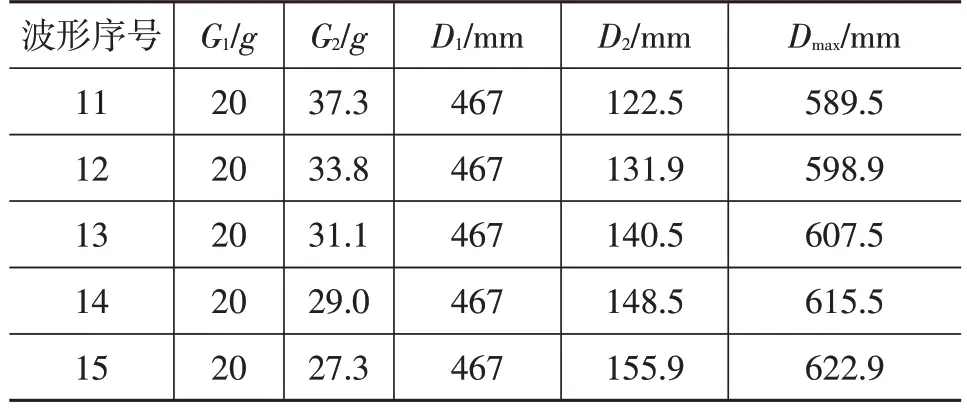
表4 不同侵入量D2等效波形參數

基于前文的標準有限元約束系統模型，對5組等效波形進行仿真計算，得到不同等效波形與損傷指標的關系如圖16、圖17所示。按照4.1節中所述方法分析左上胸部和右上胸部壓縮量，可以發現同樣規律：第64 ms時刻（轉向管柱潰縮時刻），侵入量D每增加10 mm，胸部壓縮量降低約1 mm。

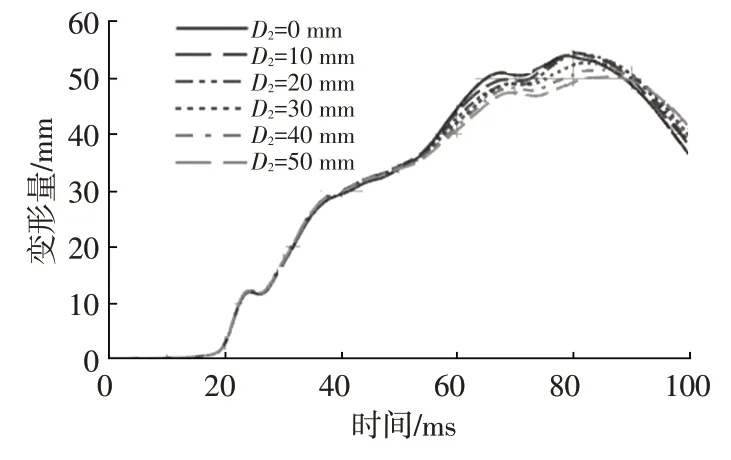
圖16 左上胸部壓縮量

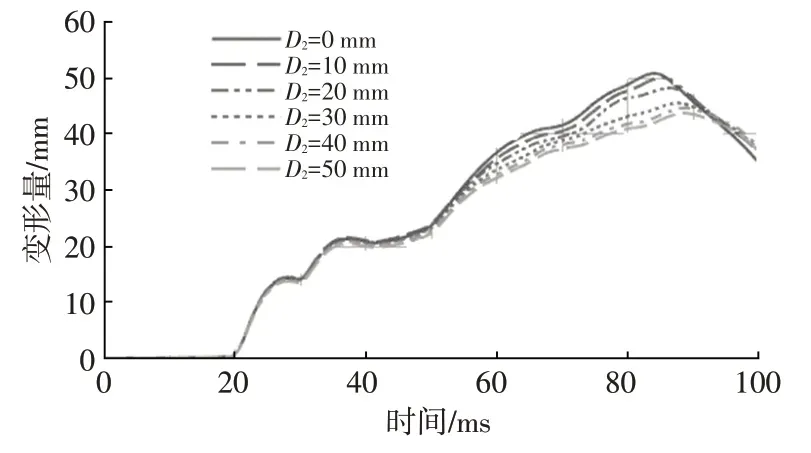
圖17 右上胸部壓縮量

5 基于量化關系的乘員損傷優化

5.1 基于量化關系的結構設計優化

為了驗證所得量化關聯關系的準確性，在某車型的開發過程中進行了驗證工作。某車型基于標準配置約束系統仿真模型預測胸部壓縮量最大值為53.4 mm，出現在右上肋骨位置，不滿足胸部壓縮量49 mm的開發目標。根據車體結構實際情況提出了G1提高2g和D增加10 mm的優化方案，優化前、后波形對比結果如圖18所示。分別將G1和D優化后的結構波形輸入標準約束系統有限元模型進行計算，胸部壓縮量對比如圖19所示，量化關系預測精度如表5所示。

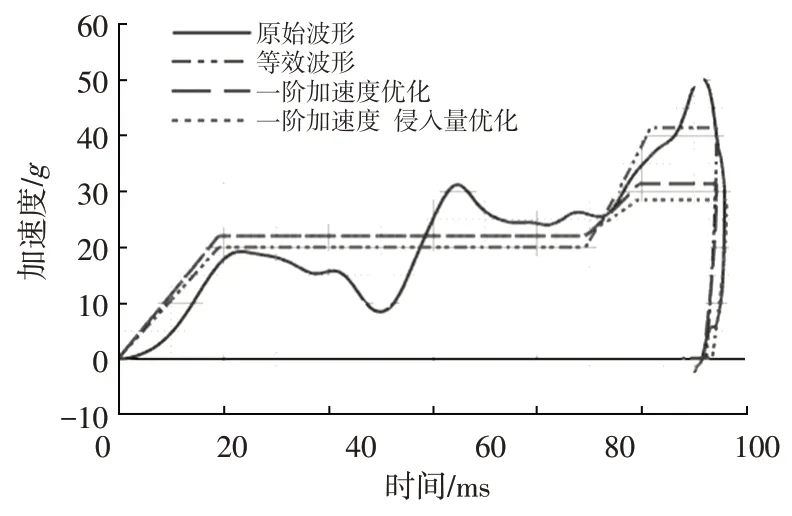
圖18 結構指標對比

5.2 基于較優車體結構的約束系統優化

5.1 節中通過量化關系對結構設計指標直接進行了優化，胸部壓縮量降低了5.1 mm，從圖19 可以看出，在第70 ms 后，胸部壓縮量再次上升并形成峰值，該處加速度主要受約束系統影響，故按照前文優化流程，基于較優車體結構進行約束系統參數優化。根據優化經驗，提出采用雙級限力安全帶優化第70 ms 后的胸部壓縮量，優化結果如圖20、圖21所示，在第70 ms時刻降低安全帶限力等級，胸部壓縮量出現明顯降低。

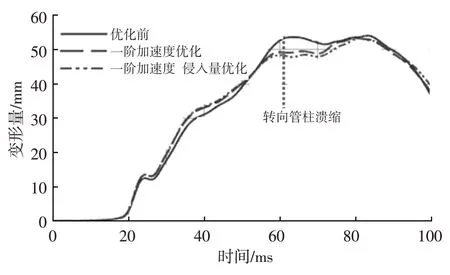
圖19 乘員損傷對比

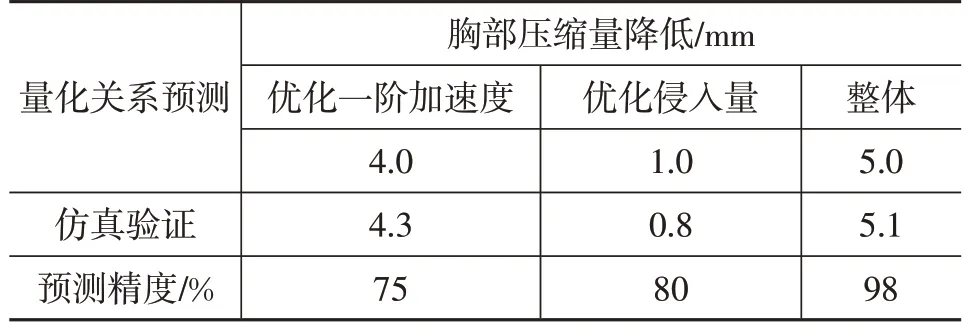
表5 量化關系預測精度

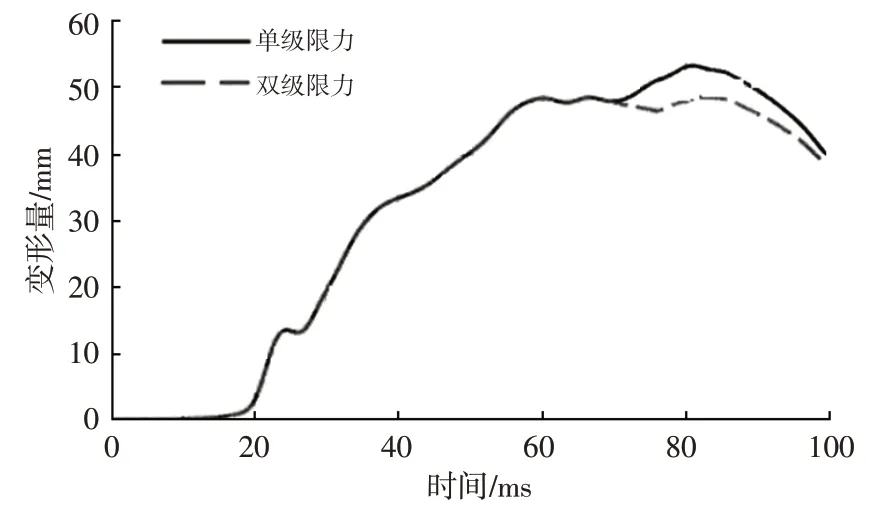
圖20 雙級限力安全帶作用下乘員損傷變化

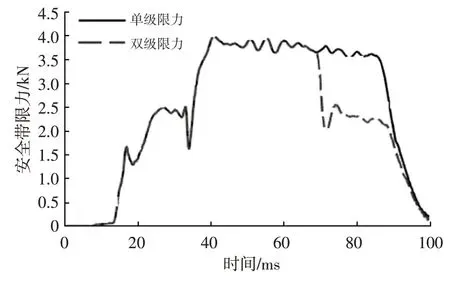
圖21 雙級限力安全帶限力特性對比

6 結束語

本文建立了標準約束系統仿真模型，以一階加速度G1、二階加速度G2、動態位移D為車體結構設計指標，胸部壓縮量為乘員損傷指標，分析獲得了不同結構下乘員損傷指標變化規律：D不變的情況下，當G1≤22g時，G1每增加1g，胸部壓縮量約降低2 mm，當G1＞22g時，其對胸部壓縮量影響較小；G1不變時，D每增加10 mm，胸部壓縮量約降低1 mm。以上述量化關系預測為基準，在某車型胸部壓縮量優化過程中對量化關系進行了驗證，結果表明，該量化關系預測精度為98%。

基于標準約束系統模型的車體結構設計指標和乘員損傷指標之間量化關系明確后，可快速根據乘員保護目標設定及優化結構設計目標，且有較高精度。

本文局限于定前懸下的車體結構設計關鍵指標研究，改變前懸長度的車體結構設計指標研究是下一步的重點工作。