基于粒子群的反應堆控制系統優化

孫 劍，俞 赟，張 瑞

(中國核動力研究設計院 核反應堆系統設計技術重點實驗室，四川 成都 610041)

反應堆控制系統(Reactor Control System，RRC)的作用是控制反應堆安全、有效地運行，使得核蒸汽供應系統生產出合格、適量的蒸汽，以實現核能向機械能、電能的轉化。在整個反應堆儀表與控制系統(I&C)中，RRC處于核心地位，是反應堆設計的重要技術領域之一。現有的主流壓水堆堆型，RRC系統都是基于經典控制理論進行設計，從結構到參數都大同小異。控制通道基于反饋、單回路、串級、前饋等經典控制理論進行設計，系統優化使用線性系統穩定性分析理論，用頻域指標界定系統的瞬態性能，從而尋找最優化控制系統參數。

本文針對反應堆控制系統參數優化問題，提出了一種新的優化設計方法，從優化結果和操作的簡易性上都要優于現有的工程方法，并且使用時不用完全替代老方法，方便在工程上使用。為了說明該方法的操作流程和效果，以穩壓器壓力控制為實例，編制了完整的程序，對比了兩種方法的優化過程及結果。

1 總體結構反應堆控制系統參數優化

問題

控制系統參數是通過對單個系統進行仿真優化得出，現有的工程優化方法具體操作流程如下：通過選定幾組可能的控制器參數及控制通道整定值，分別分析其經典控制理論頻域指標(如Nichols曲線所揭示的幅值增益、相位增益等)，以判斷不同參數組合下線性系統的時域性能(超調量、調節時間等)，通過分析和比對，找出優化后的各控制系統整定值。

在使用頻域指標考察控制系統的時域性能時，主要考慮幅值增益和相位增益指標。簡單的來說，幅值增益小于0 dB，則系統不穩定；相位增益小于0°，則系統不穩定。RRC系統的分析不僅要求系統穩定，更要求系統具有一定的穩定程度，即考慮系統參數不確定性情況下，系統仍然是穩定的，時域指標也是接近最優的。這就要求RRC系統的參數設置要使幅值增益和相位增益合適，因為幅值增益越大，系統的響應越遲緩；相位增益越大，系統越震蕩、調節時間越長；相位增益越小，超調量越大。

進一步分析，幅值增益揭示了RRC系統的閉環增益增大多少倍，系統開始變到臨界穩定和不穩定狀態。一般來說，幅值增益應大于6 dB。對于如式(1)所示的典型二階系統，其相位增益可以表達為式(2)。

(1)

式中:ωn——無阻尼震蕩角頻率;

ξ——阻尼系數。

(2)

式中:φ——相位增益。

對于2階系統，超調量可以表示為式(3)：

(3)

因此，可以通過相位增益φ求出阻尼系數ξ，進而求出超調量σ。為了折中考慮超調量和調節時間性能，應盡量使相位增益φ在30°～60°。

當RRC各控制系統整定值均已優化完成之后，需要對RRC所有控制系統進行聯合仿真分析(反應堆對象使用數字化仿真模型)，以確定各控制系統在相互配合時，整個反應堆控制系統性能指標得到了滿足，并且驗證RRC系統能夠應對電廠正常運行瞬態(階躍變化10%FP的瞬態、線性變化5%FP/min的瞬態、汽機甩負荷到廠用電瞬態和緊急停堆瞬態)，不會觸發保護系統動作。

2 設計特點傳統參數優化方法的不足及最優化改進

傳統參數優化方法在解決反應堆控制系統參數優化問題時，需要解決頻域指標和時域指標的復雜對應關系，操作起來較為復雜，且參數組合的選取采用人為試湊方式，不能涵蓋所有可能的控制系統參數組合。RRC控制系統優化的結果是一組相對優化的參數組合，并非最優化參數，這也是傳統參數優化方法的不足之處。

這是由兩方面原因引起。一方面，20世紀60年代，計算機還不夠普及，計算性能也不夠強大，還無法通過高效地計算控制系統動態響應的方式進行參數優化，只能使用頻域計算間接推斷控制系統的時域性能。在最初的頻域分析時甚至只能通過手繪方式計算Nichols曲線，而以這種方式完成RRC系統的優化將是十分龐大的工作量。再者，當時情況下，工業領域可選擇的控制領域的理論工具十分有限。對于反應堆控制系統參數優化問題，研究使用群體智能算法來求解將是一個很好和可行的嘗試。這樣做優點是顯而易見的，首先是可以對一個大的參數范圍進行搜索，其次充分利用計算機的能力，直接用時域響應作為評判指標，從而得到一組最優化的控制系統參數。

3 基于粒子群算法的反應堆控制系統最優化

3.1 粒子群優化算法簡介

粒子群優化算法是基于群智能方法的演化算法，由美國社會心理學家Kenndy和電氣工程師Eberhar于1995年提出。基本概念源于對鳥群捕食行為的研究，鳥群在飛行過程中經常會突然改變方向、散開、聚集，其行為不可預測，但整體總保持一致性，個體與個體之間也保持著最適宜的距離。研究發現，鳥僅僅追蹤它有限數量的鄰居，但最終的整體結果是整個鳥群好像在一個中心的控制之下，即復雜的全局行為是由簡單規則的相互作用引起的，生物群體之間存在著一種社會信息共享機制，為群體的進化提供了一種優勢。使用計算機模擬鳥群的覓食行為，可用于解決優化問題。基本原理如下：問題的解對應于搜索空間中粒子的位置。每個粒子有自己的位置和速度(決定飛行的方向和距離)，還有一個由被優化函數決定的適應值。各個粒子記憶、追隨當前的最優粒子，在解空間中搜索。每次迭代的過程不是完全隨機的，如果找到較好解，將會以此為依據尋找下一個解。

算法描述如下：隨機初始化一群粒子，其中第i個粒子在D維解空間的位置表示為xi=(xi1,xi2,…,xiD)。每一次迭代，粒子通過動態跟蹤兩個極值來更新其速度和位置。第一個是粒子從初始到當前迭代次數搜索產生的最優解：個體極值pBesti=(pi1,pi2,…,piD)；第二個是粒子種群目前的最優解：全局極值gBest=(g1,g2,…,gD)。第i個粒子根據以下公式來更新其第d維(1≤d≤D)速度和位置：

vid=wvid+c1r(pid-xid)+c2R(gd-xid)

(4)

xid=xid+vid

(5)

式中:v——粒子速度;

x——粒子位置;

w——為避免粒子在全局最優解附近震蕩的可變慣性系數;

r,R——均勻分布在(0，1)區間的隨機數;

c1,c2——學習因子。

粒子在解空間內不斷跟蹤個體極值和全局極值進行搜索，直至達到規定的迭代次數或滿足規定的性能指標為止。算法流程如圖1所示。

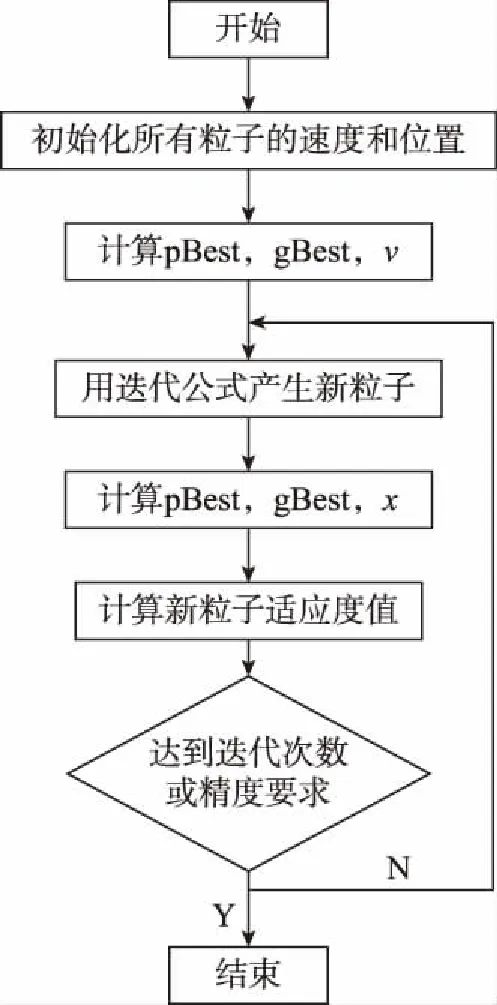
圖1 粒子群優化算法計算流程Fig.1 Calculation flow of particle swarm optimization algorithm

3.2 適應度函數

利用粒子群算法進行RRC系統參數優化時需要計算某種參數組合情況下系統的適應度值，即系統在給定控制通道參數作用下的響應性能評價。對于一般的最小相位系統，階躍響應中包含的上升時間、超調量、穩態偏差等指標足以用于評價系統的性能。為了便于計算機編程，設計如式(6)所示的指標，用于表征系統的時域性能。

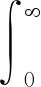
(6)

式中：e(t)——控制偏差;

t——時刻;

J——適應度函數值。

該指標對初始誤差考慮較少，而主要限制過渡過程后期出現的誤差，即控制系統評價考慮的是對誤差的消除能力再加上時間的懲罰項。該指標綜合了上升時間、超調量、穩態偏差等指標，J值最小的控制系統參數可被看作是最優化的控制系統參數，而控制參數最優化的迭代過程則由粒子群算法解決。

3.3 控制通道的高速計算機仿真

使用粒子群優化控制系統參數時，計算量大，粗略估算總耗時為：每一次控制參數性能評價時間、粒子群種群規模和最大學習代數三者的乘積。對于每一次控制參數性能評價，需要計算控制通道的階躍響應，而對反應堆控制系統涉及的大部分對象，至少需要計算600～1 000 s范圍內系統的響應才有意義。由此可見，使用粒子群算法進行反應堆控制系統參數優化的計算量十分龐大，若算法設置不合理，將導致整個優化過程漫長。

本文在進行控制通道階躍響應計算時，沒有直接利用連續系統離散化的現成軟件包，而是采用對復雜傳遞函數進行技巧性拆分，分成基本環節的組合，然后利用離散相似法計算得出快速運算的差分方程。這樣做的優點是便于編制計算機迭代程序，提高運算速度。

例如，圖2所示的復雜傳遞函數：

圖2 復雜傳遞函數的拆分Fig.2 Splitting of complex transfer functions

對于積分環節有式(7)，其中ts是采樣周期。

x2(k+1)=x2(k)+k·x1(k)×ts

(7)

(8)

根據離散相似法公式：

x(k+1)=eAts·u(k)+

(9)

當采用零階保持器時，慣性環節的差分方程可以寫為:

(10)

(11)

利用上述，圖2的控制通道就能在計算機上進行高速仿真。

4 實例分析

4.1 穩壓器壓力控制系統優化問題描述

下面以國內典型三環路M310機組的穩壓器壓力控制系統優化為例，說明控制系統參數優化的過程。簡化的控制邏輯如圖3所示，控制目標是在正常運行瞬態將穩壓器壓力控制在15.5 MPa abs，而不引起停堆或穩壓器安全閥開啟。控制手段有兩個，2組比例式電加熱器通過增加水的閃蒸來提高穩壓器壓力，兩條噴淋管線通過控制冷水噴淋流量來降低壓力。兩個非線性環節用來使得電加熱器和噴淋流量按順序投入運行。

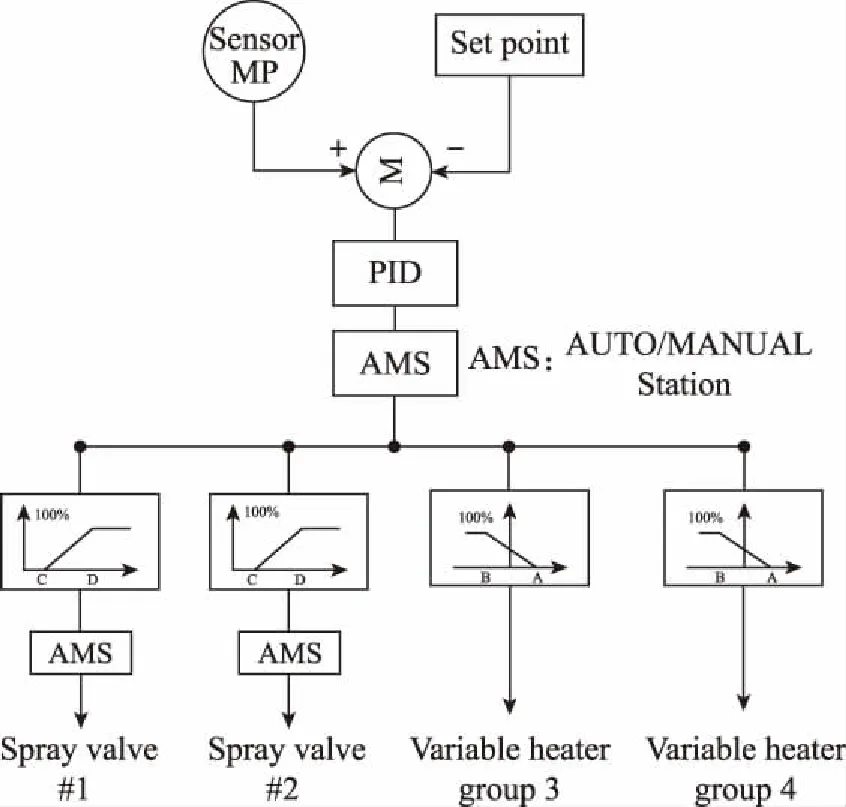
圖3 穩壓器壓力控制簡化邏輯圖Fig.3 Simplified logic of pressure control for the pressurizer

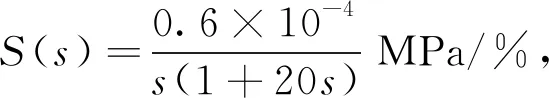
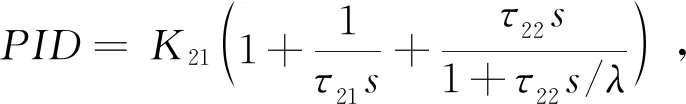
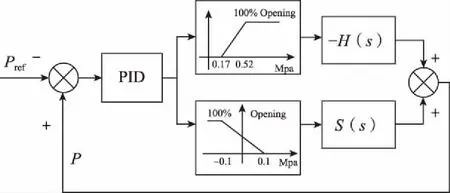
圖4 穩壓器壓力控制參數優化完整框圖Fig.4 Complete block diagram of pressure control parameter optimization of the pressurizer

4.2 基于古典控制理論的參數優化

使用電加熱器改變穩壓器壓力是一個緩慢的過程，而噴淋相對而言快速得多。因此，可以大致將優化過程分成兩步進行。首先不考慮微分作用(即微分項置為0)，只考慮電加熱器的動作來優化積分項，主要考察控制系統消除壓力穩態偏差的能力。人為選取三組積分常數值(100 s，600 s，1 000 s)，繪制控制通道Nichols曲線如圖5。

圖5 積分項優化Fig.5 Integral term optimization

表1 控制器積分項幅值、相位增益表

可見，積分項的選取不會顯著改變幅值增益，但會顯著影響相位增益。積分項的目的是消除穩態偏差，壓力控制并不需要大的積分項，以便開關式電加熱器不會頻繁開啟，且控制通道應避免阻尼震蕩，因此選取600 s較為合適。

在積分項確定之后，第二步優化PID控制器的微分項，這主要通過對噴淋系統的分析，確定控制系統具有良好快速性的微分時間。限于篇幅，這里不再論述，優化的結果是λ=1.25，τ22=5 s。

4.3 基于粒子群算法的智能參數優化及對比分析

使用智能參數優化時，不需要針對電加熱器控制通道和噴淋控制通道單獨優化，因為這兩個通道的特性已經包含在他們的對象模型中，再者分開優化也不好界定兩個通道之間的影響程度，這也是相對于古典控制理論優化更合理的地方。

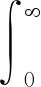
學習代數設定為最大30代，學習系數設定為典型值2.05，慣性權重設定為0.729。迭代過程適應度的變化過程如圖6，優化結果為τ21=867 s，λ=2.6，τ22=6.8 s。

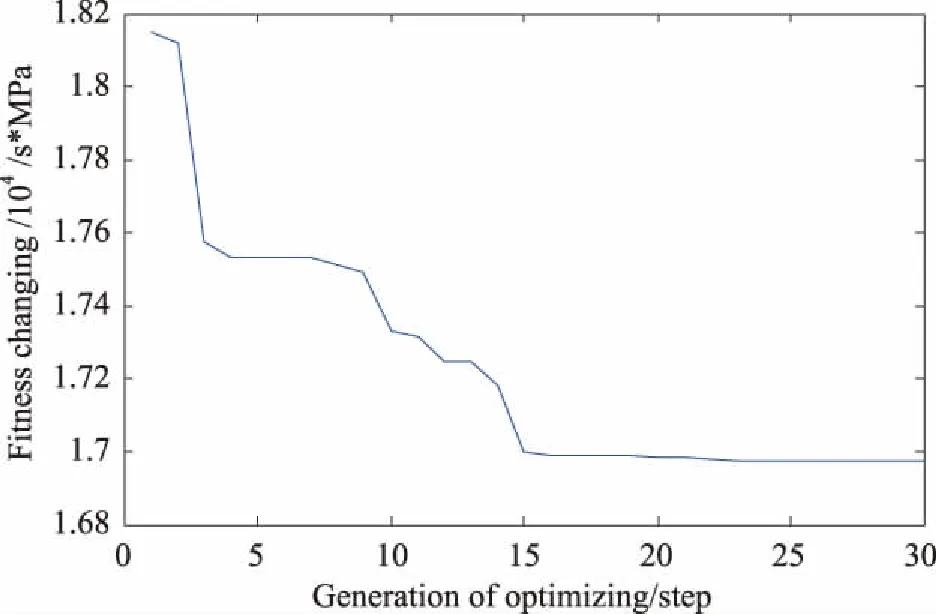
圖6 迭代過程適應度變化Fig.6 Change of fitness in iterative process

為了比較兩組參數的優劣，分別仿真壓力設定值階躍+0.2 MPa和-0.2 MPa時兩組控制參數的控制系統響應效果，對比曲線見圖7和圖8。其中，壓力階躍-0.2 MPa時，噴淋和電加熱器同時起作用。從圖中可以看出，根據古典控制理論優化出來的PID參數效果良好，但不是最優參數，粒子群算法優化的參數在超調量指標上有明顯改進，優于現有工程方法的優化結果。

對于實際工程來說，優選出來的PID參數還應考慮開關式電加熱器的動作，而這可以通過控制系統聯調來測試其性能。限于篇幅，這里不再論述。

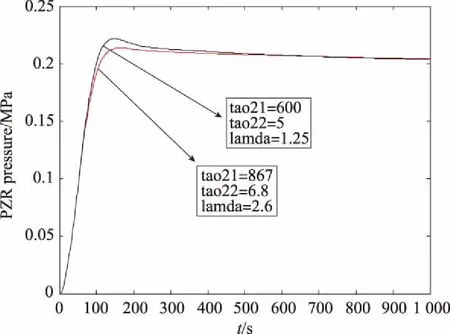
圖7 兩組PID參數控制效果對比Fig.7 Comparison of control effects of two groups of PID parameters

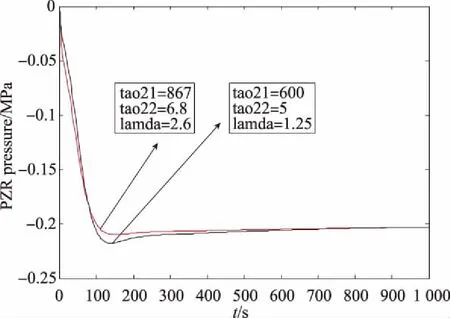
圖8 兩組PID參數控制效果對比Fig.8 Comparison of control effects of two groups of PID parameters

5 結論

隨著計算機的出現和處理能力的提升，幾乎所有工業領域都產生了革命性發展。反應堆控制系統設計也應緊跟潮流，一方面利用計算機的能力提升設計水平，另一方面在過程控制中改進整個系統的性能。

本文論述了反應堆控制系統參數優化的過程和理論，闡明了現有的工程優化方法及其不足之處，提出了基于粒子群優化的新方法。該方法利用現代計算機高速計算的能力，對反應堆控制系統的參數進行最優化搜索。相對于目前工程中使用的方法，新方法能夠做到最優化設計，且優化過程更為直接、直觀，并且以穩壓器壓力控制系統的優化為例，測試了新方法的有效性，為工程使用打下了基礎。