多波長明渠非恒定流傳播特性研究

古宇翔，楊勝發，黃 岱，胡 江

(1.重慶交通大學河海學院，重慶 400074；2.國家內河航道整治工程技術研究中心，重慶 400074；3.北海道大學大學院工學研究院，日本 北海道 060-8628)

非恒定流是指水流的運動要素隨時間過程而變化的流體運動。在現實情況中，河道水庫潰壩、洪水演進、船閘充排水、水電站泄洪日調節等[1-7]均為典型的非恒定流問題。而大多數明渠非恒定流以多波長的形式進行傳遞。

多波長明渠非恒定流傳播的一維數值模擬是以圣維南方程組為基礎，通過有限差分法對方程組離散化處理。從20世紀90年代開始，學者們主要采用顯式差分法和Preissmann隱式差分法對明渠非恒定流進行數值模擬。吳至維等[8]用顯式擴散差分格式對模擬情況進行求解，并討論了權因子的取值。蔣艷等[9]用Preissmann四點偏心隱格式對長江江蘇段內水流進行了計算。Freitag[10]討論了Preissmann四點偏心隱格式在計算跨臨界流中會不穩定的情況，以改進后的Thomas追趕法解Preissmann四點偏心隱格式。上述研究均取得了較好的成果，但傳統差分方法計算仍然存在一定的局限性。因此本文提出了一種新型的隱式迭代法，對多波長明渠非恒定流進行數值模擬及水槽試驗驗證，并以長距離水槽模擬的方式對多波長明渠非恒定流的傳播特性進行深入研究。

1 一維非恒定流數學模型的建立

1.1 傳統差分方法的比較

有限差分法分為顯式差分法和隱式差分法。顯式差分法計算方便，但對于明渠計算區域過長的情況，其計算的穩定性不高，計算結果會出現較大誤差。隱式差分法選定合適的權因子后，可達到無條件穩定，但隱式差分法適用于水流變化較為緩慢的工況，且需要同時具備上下游邊界條件，否則無法進行準確的計算。針對傳統有限差分方法的計算缺點，本文提出了一種優化的隱式迭代計算方法。

1.2 隱式迭代法的計算步驟

將圣維南方程組轉化為以下形式：

(1)

(2)

其中 ?x為斷面間距;?t為時間步長;Q為流量;A為橫斷面面積;h為水深;g為重力加速度;z為水位;K為流量模數。

當R=0時，滿足圣維南方程組的求解。采用Preissmann隱格式的四點網格布置，取權系數θ=1，可得到:

(3)

(4)

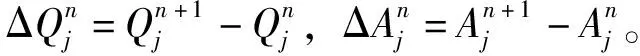
2 一維非恒定流數學模型的驗證

在水槽一維非恒定流數學模型的驗證中，參照胡江[11]的研究成果，對相應工況進行驗證。試驗在 28 m×0.56 m×0.7 m的玻璃水槽中進行，糙率取0.015。水槽配備水泵、變頻器與流量計組成的水循環系統，并沿程布置了8個超聲水位計探頭，實時測量沿程水位(水槽構造見圖1所示)。

圖1 28 m玻璃水槽構造示意

試驗將對水槽典型斷面的水位、流量和波形特征進行驗證。取水流波形相對穩定，距離水槽進口19.05 m處的6#超聲水位計所在斷面為典型驗證斷面。

2.1 水位、流量驗證

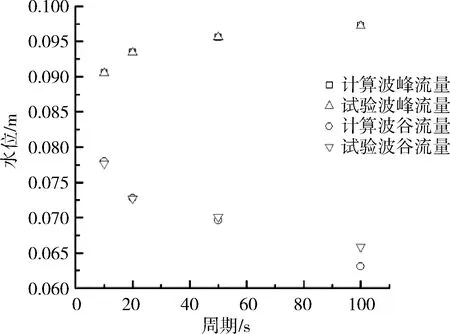
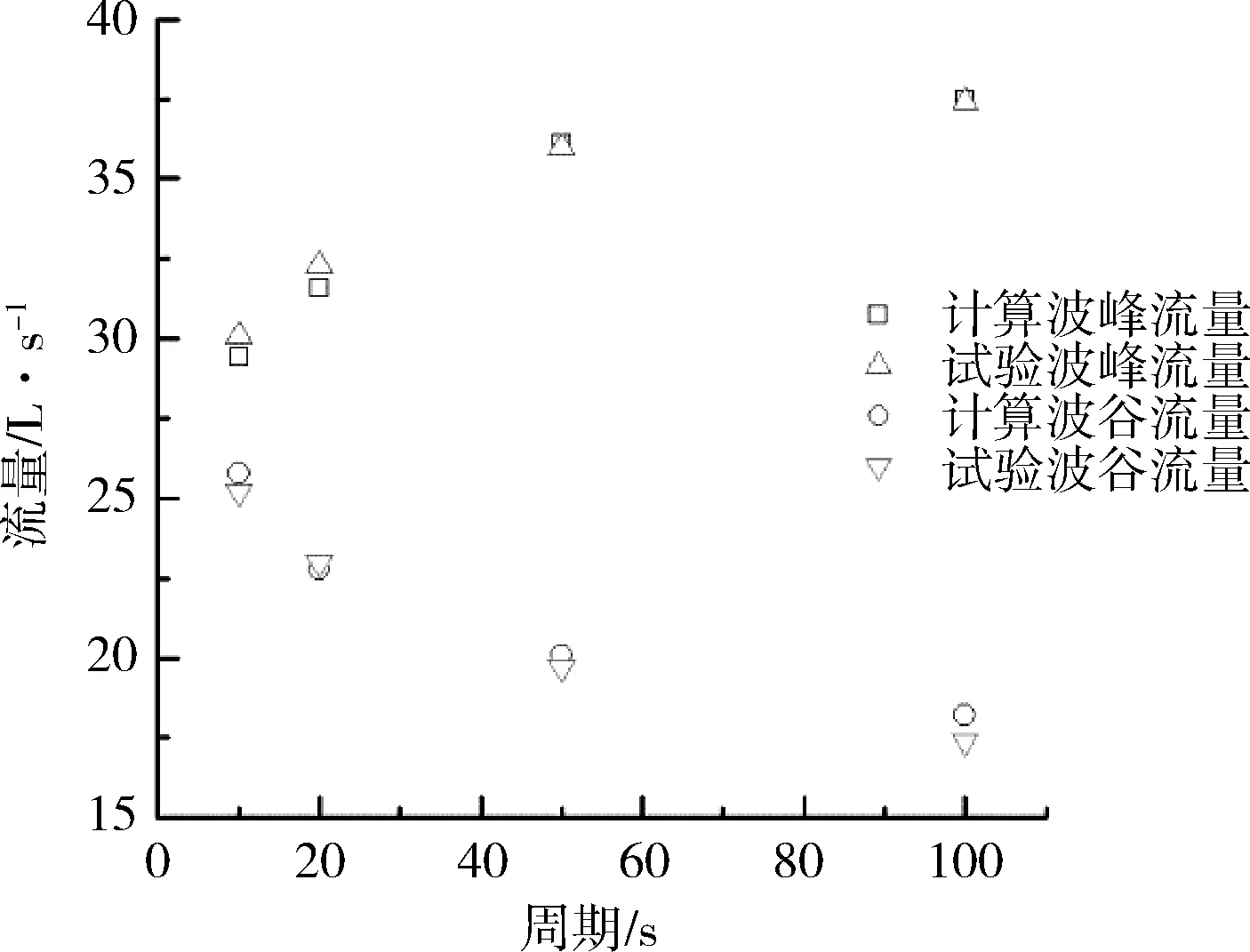
采用進口流量變化為15～40 L的工況，變化周期分別為10 s、20 s、50 s和100 s，波形為正弦波，以波谷出現時為0 s起點。對應的計算模型時間步長Δt分別為0.2 s，0.4 s，1 s和2 s，斷面間距Δx分別為0.06 m，0.12 m，0.3 m和0.6 m。典型斷面的水位、流量計算結果驗證見圖2。

由圖2(a)可知，典型斷面波峰水位的計算值與實測值的誤差很小，最大誤差在周期為100 s處的波谷處，為0.002 78 m，誤差百分比為4%。由圖2(b)可知，試驗與計算波峰流量誤差值最大為0.769 L/s，最大誤差百分比為2.3%；試驗與計算波谷流量誤差值最大為0.8 L/s，最大誤差百分比為4.6%。計算結果基本滿足誤差要求。

(a)水位驗證

(b)流量驗證

2.2 波形特征驗證

采用進口流量變化為15～40 L的工況，變化周期為10 s。計算模型時間步長Δt為0.2 s，斷面間距Δx為0.06 m。典型斷面的波形特征驗證結果見圖3。

由圖3可知，試驗水位波峰出現時間為3.4 s，計算水位波峰出現時間為3.5 s，誤差為2.9%。波形吻合良好，計算結果基本滿足誤差要求。

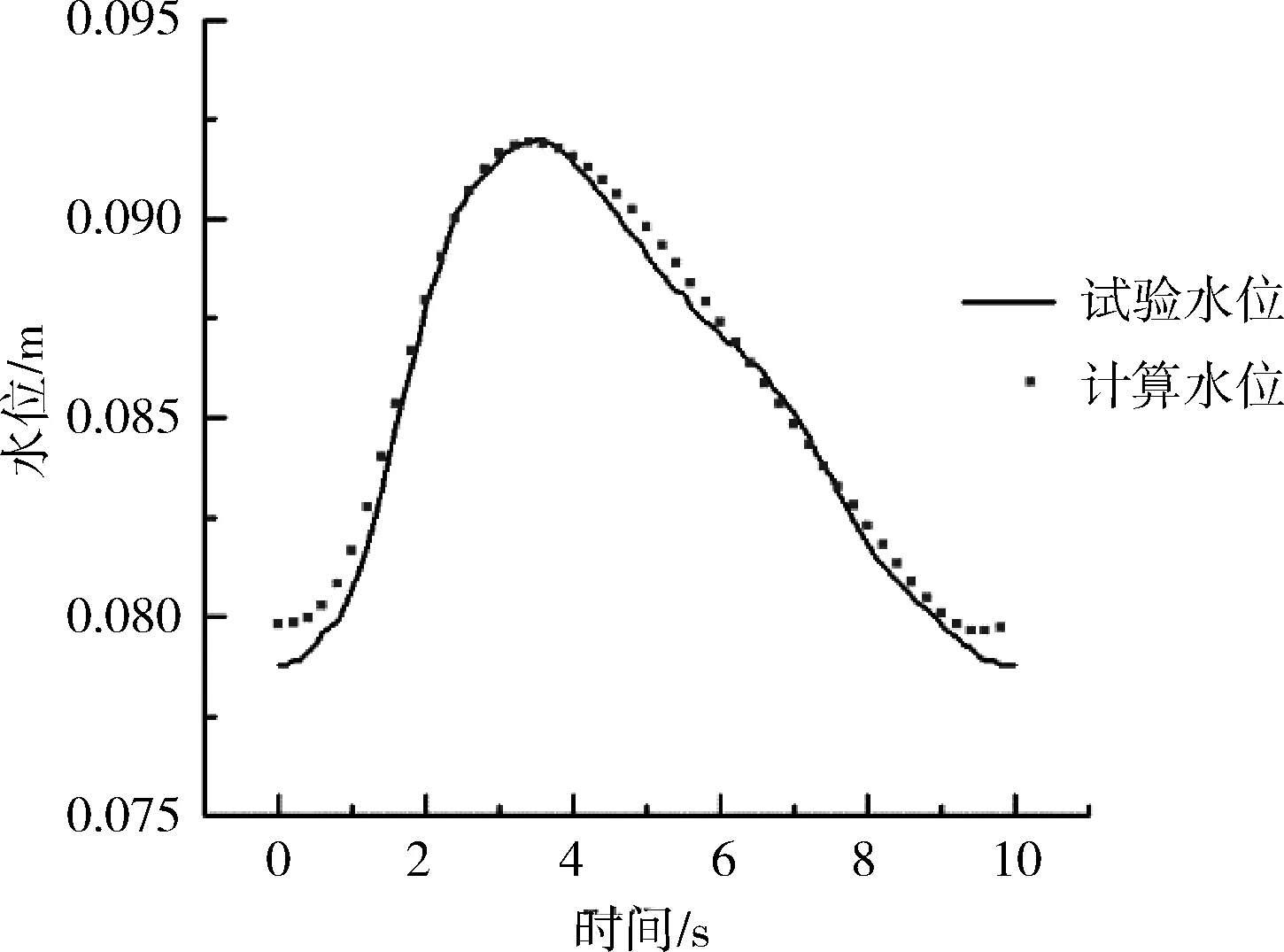
圖3 典型斷面波形特征驗證

3 多波長非恒定流的水槽模擬

在第2節中，通過水槽試驗對隱式迭代法的數值模擬結果進行了驗證，效果良好。為了更好地研究多波長明渠非恒定流的傳播特性，本節模擬了矩形水槽中的非恒定流的傳播，并從非恒定流的傳播速度和衰減特性兩方面來討論非恒定流的傳播特征。

3.1 模擬工況的設定

計算模型的輸入條件為初始斷面(水槽進口斷面)的流量—水位過程。在初始斷面，當水位h和過水斷面寬度B滿足h

Q=1/n·Bh5/3J1/2

(5)

其中Q為流量，n為糙率，J為比降。由初始斷面流量過程，可得到初始斷面水位過程。計算開始之前，默認各斷面初始時刻的流量和水位相同，即為恒定流。

在模擬水槽中，水槽寬度B=1 m，糙率n=0.035。計算模型的時間間隔Δt始終滿足Δt=T/50(即為1個變化周期的1/50)，且與斷面間距Δx滿足數值關系Δx=0.3Δt。模擬水槽長度為2 000Δx，程序運行周期為13T。比降與進口流量變化的數值將作為非恒定流傳播特性的影響因素。

3.2 不同條件下明渠非恒定流的傳播速度

本研究中模擬了不同比降和不同流量下明渠非恒定流的傳播速度，計算工況如下：

不同比降：流量過程為15～40 L/s，周期為50 s，比降J為0.5‰，1‰，2‰和3‰。共統計8個周期。

不同流量：考慮到在模擬條件中，水深h和過水斷面寬度B滿足h

對速度沿波長數k的衰減進行擬合。由圖4可知，非恒定流的傳播速度趨勢是和流速是一致的。比降越大，流速越大，則非恒定流的傳播速度越快。同理，流量越大，流速越大，非恒定流的傳播速度也會加快。

在波峰均值較大的第一個周期，傳播速度更快，隨著波峰沿程降低，傳播速度逐漸變慢平穩，并趨近于一個定值。波速可視為由變幅波速和基礎波速組成。變幅波速受到本身的變幅影響，隨著非恒定流衰減而減小；基礎波速則取決于整體流動，整體流速越快，基礎波速越大，其在非恒定流的傳播中起主導作用。

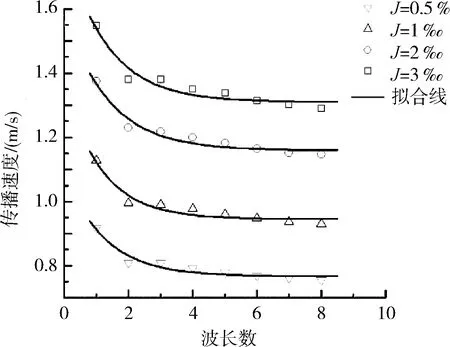
(a)不同比降

(b)不同流量過程

3.3 不同條件下明渠非恒定流的流量變幅衰減特性

非恒定流的流量變幅是指在一個計算周期內最大流量與最小流量的差值。為了研究非恒定流流量的衰減特性，需要保持初始條件的流量變幅相同，即ΔQ相同。

采取了以下工況：

工況1：流量過程為15～40 L/s，周期為50 s，比降為0.5‰，1‰，2‰和3‰。

工況2：流量過程為5～30 L/s，15～40 L/s和25～50 L/s，周期為50 s，比降為1‰。

由圖5可以得到結論：比降越大，沿程流量變幅衰減越慢；比降越小，沿程流量變幅衰減越快。同理，平均流量越大，沿程流量變幅衰減越慢；平均流量越小，沿程流量變幅衰減越快。根據圖5還能推測得出：比降較小或者平均流量較小的情況下，流量沿程衰減較快是因為其非恒定流的傳播速度較慢，相應的波長較短，導致非恒定流傳播過相同距離時，傳播速度較慢的非恒定流需要更多的周期數。同時，由于在固定周期內流量變幅基本相同，所以在相同距離內，傳播速度較慢的非恒定流會較傳播速度較快的非恒定流衰減較多的次數，所以會造成非恒定流沿程衰減較快。

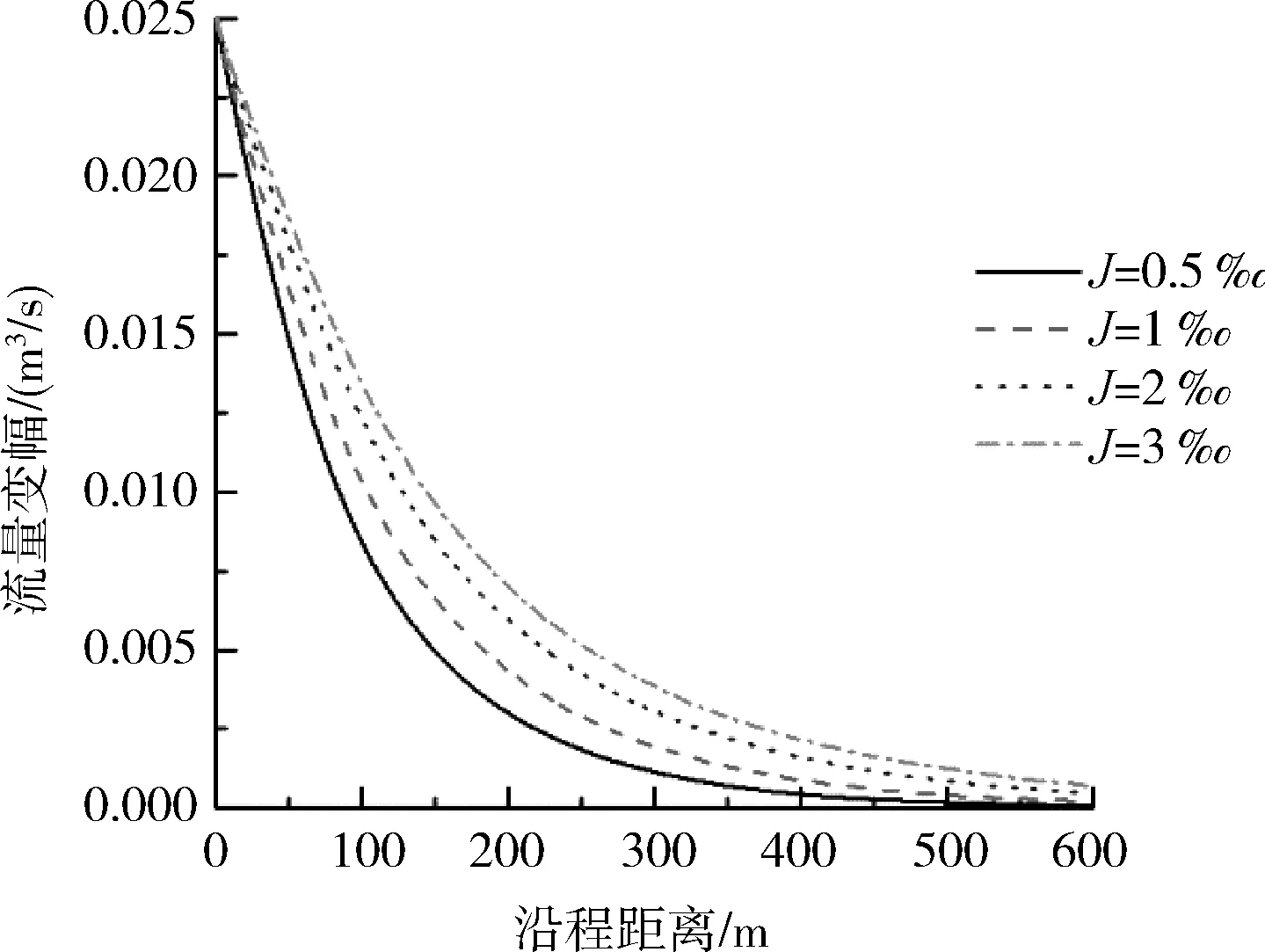
(a)不同比降

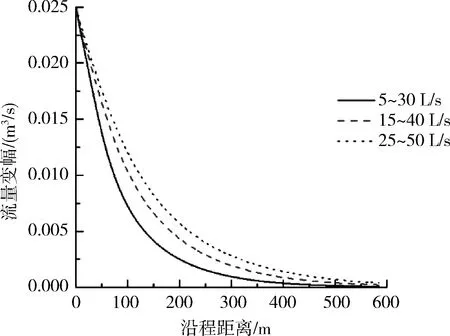
(b)不同流量過程

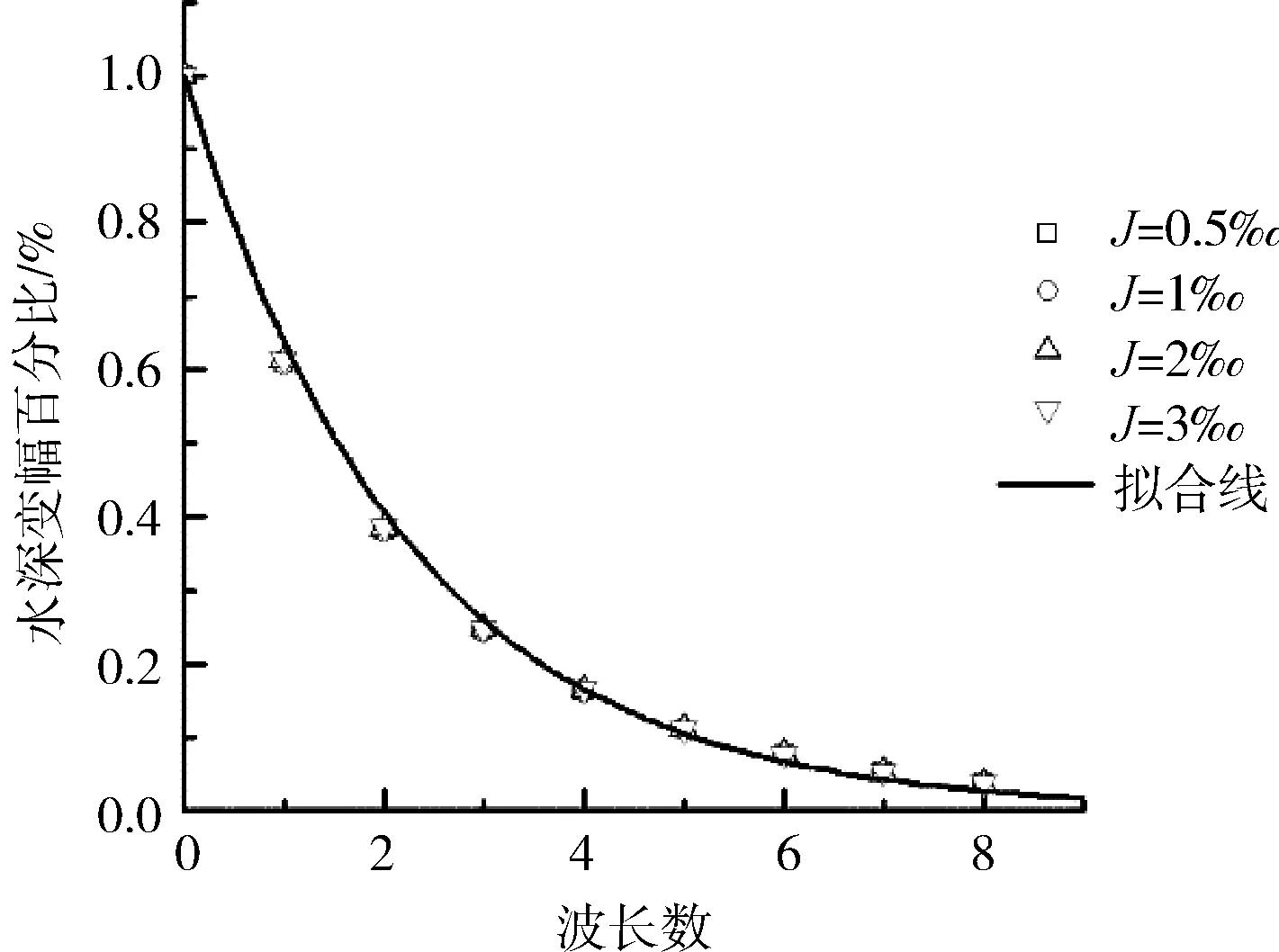
由圖6(a)可知，相同波長內的變幅差值百分比最大不超過1%，差異一般在0.5%之內。圖6(b)中，對于主要體現非恒定流波動性質的前端(第一波長到第四波長)，誤差百分比最大值為3.3%。可以得出結論：非恒定流隨周期衰減的特性和比降以及平均流量關系不大。

(a)不同比降

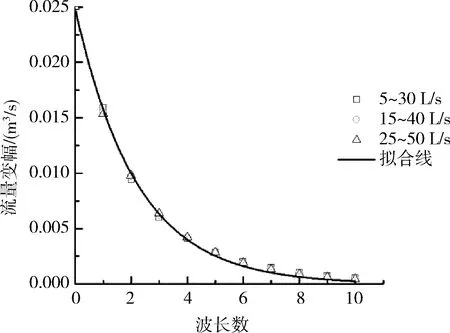
(b)不同流量過程

此外本文對圖6中的計算數據點進行了擬合，得到了水深變幅的指數型擬合曲線：

ΔQn=ΔQ0·e-0.45k

(6)

綜上所述，在初始斷面流量變幅相同的情況下，流速越快則流量變幅沿程衰減越慢，但在一個波長內，流量變幅的衰減是幾乎相同的。

3.4 不同條件下明渠非恒定流的水深變幅衰減特性

在3.3節的工況下，由于比降和平均流量的差異，會導致水深整體抬高或降低，這樣并不利于水深變幅的比較，故統計了各斷面相對初始斷面的水深變幅衰減百分比，即Δhj/Δh1×100%。采用與3.3節相似的方法統計水深變幅的衰減特性。

由圖7～8可以得出，水深變幅與流量變幅有著較好的一致性，即：比降越大，沿程水深變幅衰減越小，比降越小的情況下水深變幅會越快趨近于平穩；平均流量越大，沿程水深變幅衰減越小，平均流量越小的情況下水深變幅會越快趨近于平穩。

(a)不同比降

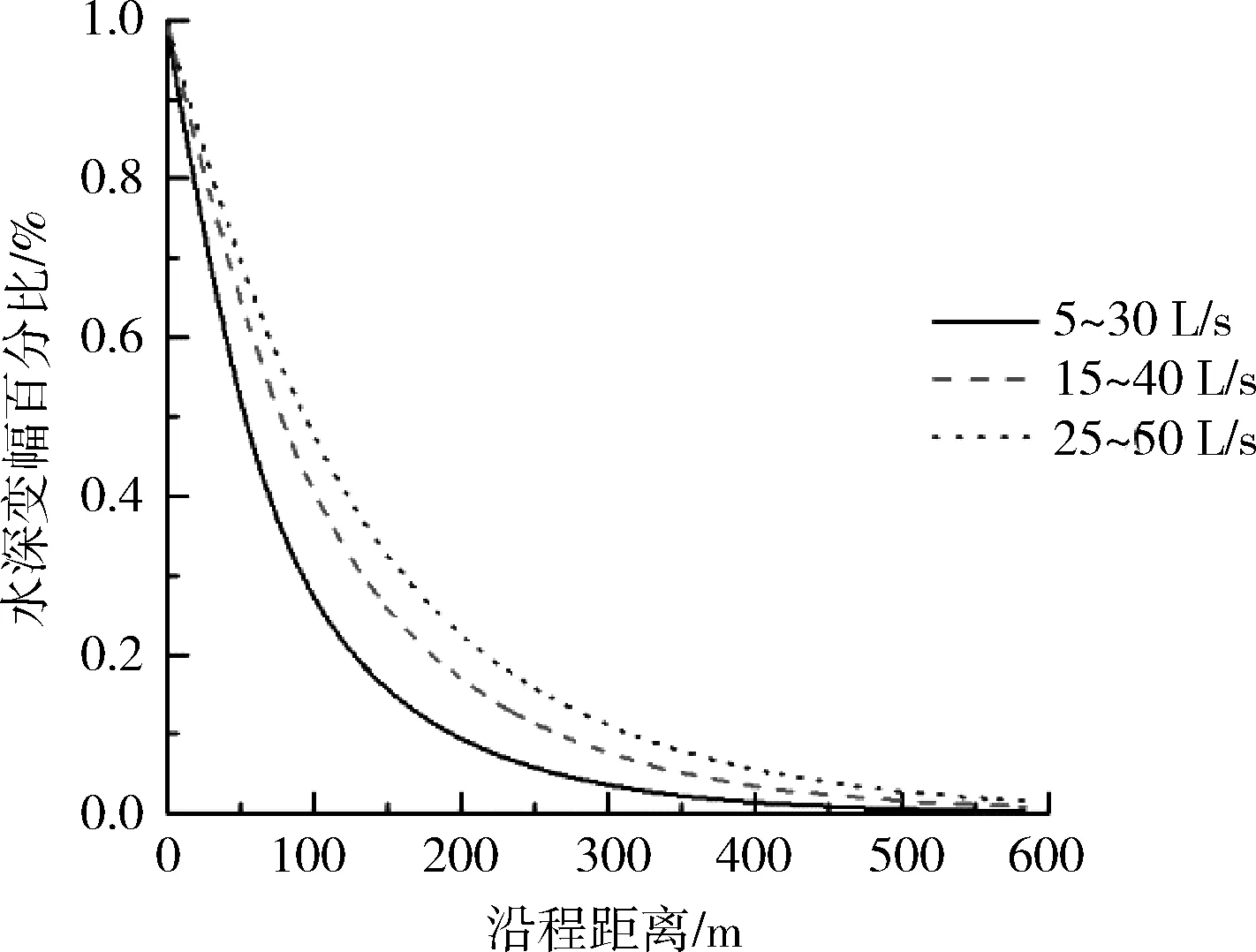
(b)不同流量過程

(a)不同比降

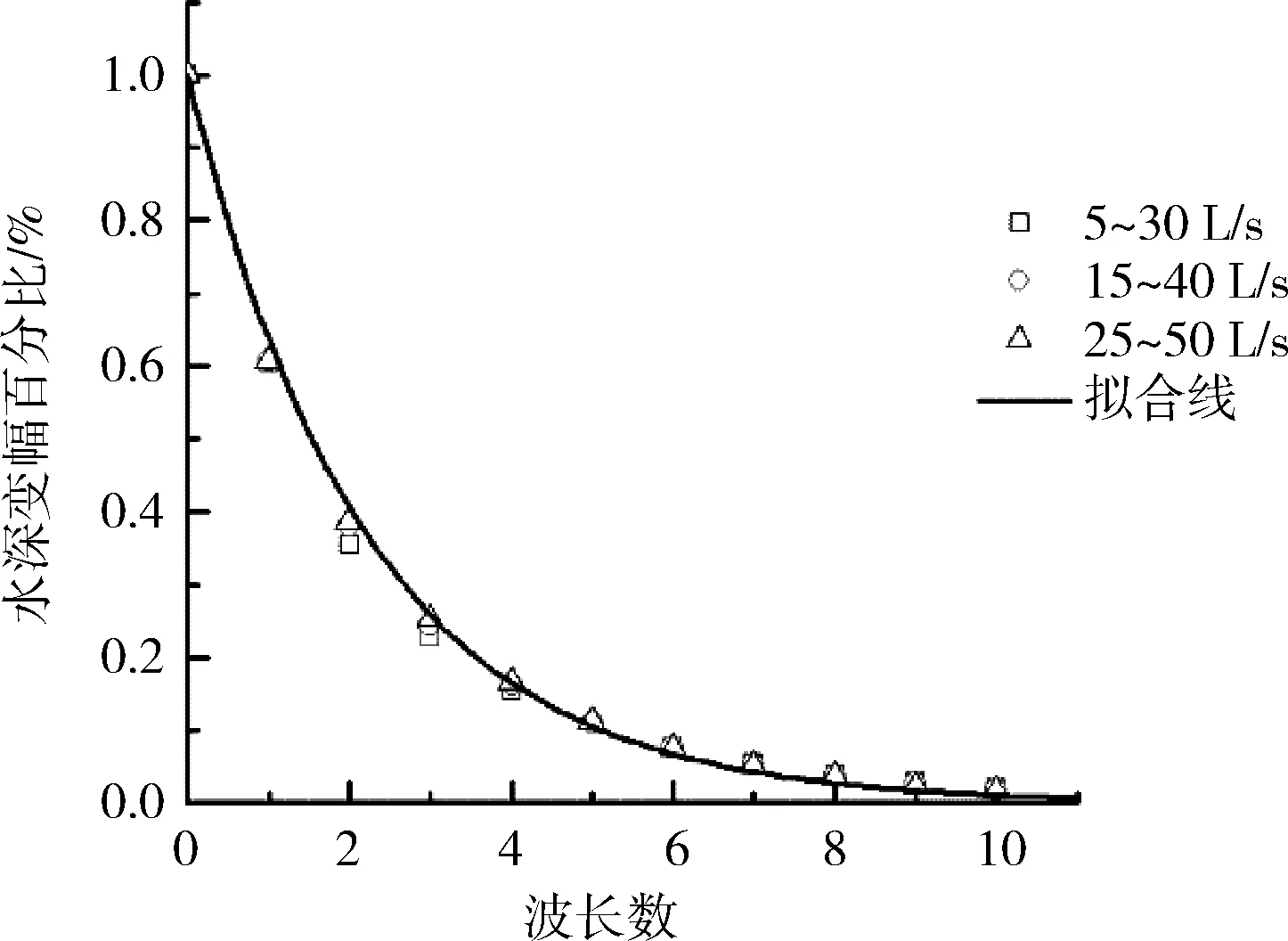
(b)不同流量過程

同樣，以非恒定流傳播周期為參照單位時，各種工況下水深變幅基本相等。在不同比降下，相同波長內的水深變幅百分比差異一般在1%之內，最大差異出現在尾部第九周期，為1.2%。在不同平均流量下，對于主要體現非恒定流波動性質的前端(第一波長到第四波長)，誤差百分比最大值為6.1%。擬合曲線為：

Δhn=Δh0·e-0.45k

(7)

其中hn為第k個波長處的水深變幅的衰減百分比；h0=1。

綜上所述，在初始斷面流量變幅相同的情況下，水深變幅的衰減和流量變幅的衰減具有一致性，流速越快則水深變幅沿程衰減越慢，在一個波長內，水深變幅的衰減幾乎相同。

4 結語

本文針對傳統有限差分法的局限性，提出了適用于多波長明渠非恒定流數值模擬的新型隱式迭代法。通過水槽試驗驗證：新型的隱式迭代法計算結果精度高，與實測結果相比誤差小，能夠很好地適應多波長明渠非恒定流的數值模擬。

通過對多波長明渠非恒定流過程的水槽模擬以及對不同比降和平均流量的工況對比，得出了多波長明渠非恒定流有以下傳播特性：

1)明渠非恒定流的傳播速度和流量、水深變幅，會隨著傳播而沿程衰減，且衰減幅度會逐漸減小，最終趨于穩定。

2)對于進口流量變幅相同的工況，流量和水深變幅的衰減百分比在相同波長內幾乎完全一樣。

3)非恒定流的傳播速度主要取決于流速大小，流速越大傳播越快，流速越小傳播越慢，且其傳播速度會在第一個波長到第二個波長內迅速衰減。

4)不同比降和不同平均流量對非恒定流沿程衰減的主要影響是通過影響其傳播速度從而改變其沿程衰減的情況。在高比降、大平均流量的情況下，非恒定流沿程傳播速度較快，通過相同的距離時所需的周期數較少，導致衰減較慢；在低比降、小平均流量的情況下，非恒定流沿程傳播速度較慢，通過相同的距離時所需的周期數較多，導致衰減較快。