基于MATLAB的微軸承動力學特性的數值分析*
蘭正義,伍 林*,呂剛磊
(1.上海應用技術大學 機械工程學院,上海 201418;2.鄭州科技學院 機械工程學院,河南 鄭州 450064)
0 引 言
目前,微機電系統下微軸承—轉子系統穩定性的判斷分析,主要是結合微軸承的動力學特性系數進行分析而獲得,但大部分的動力學特性參數計算是在基于不考慮氣體滑移的連續模型下獲得的[1-2]。
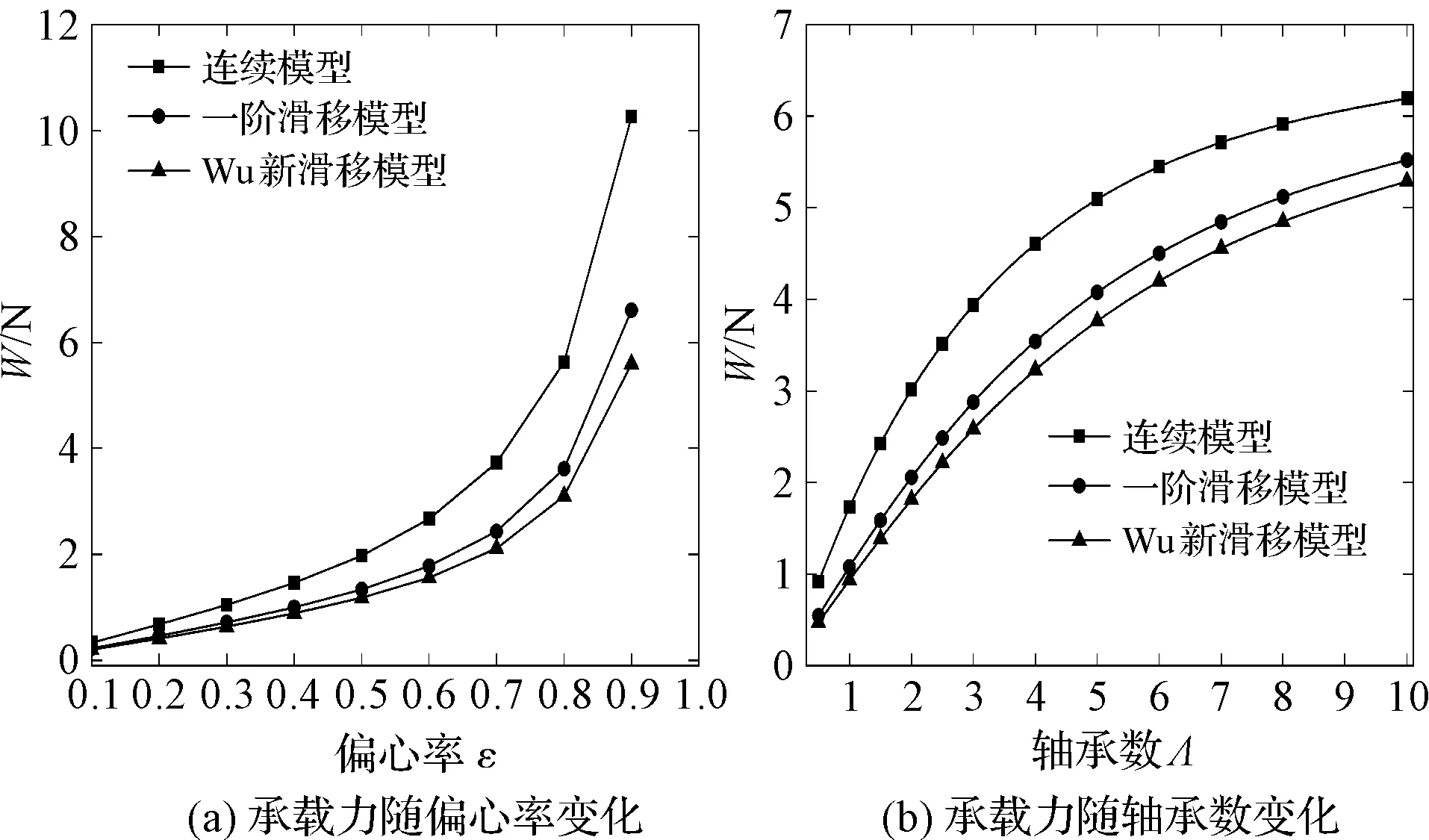
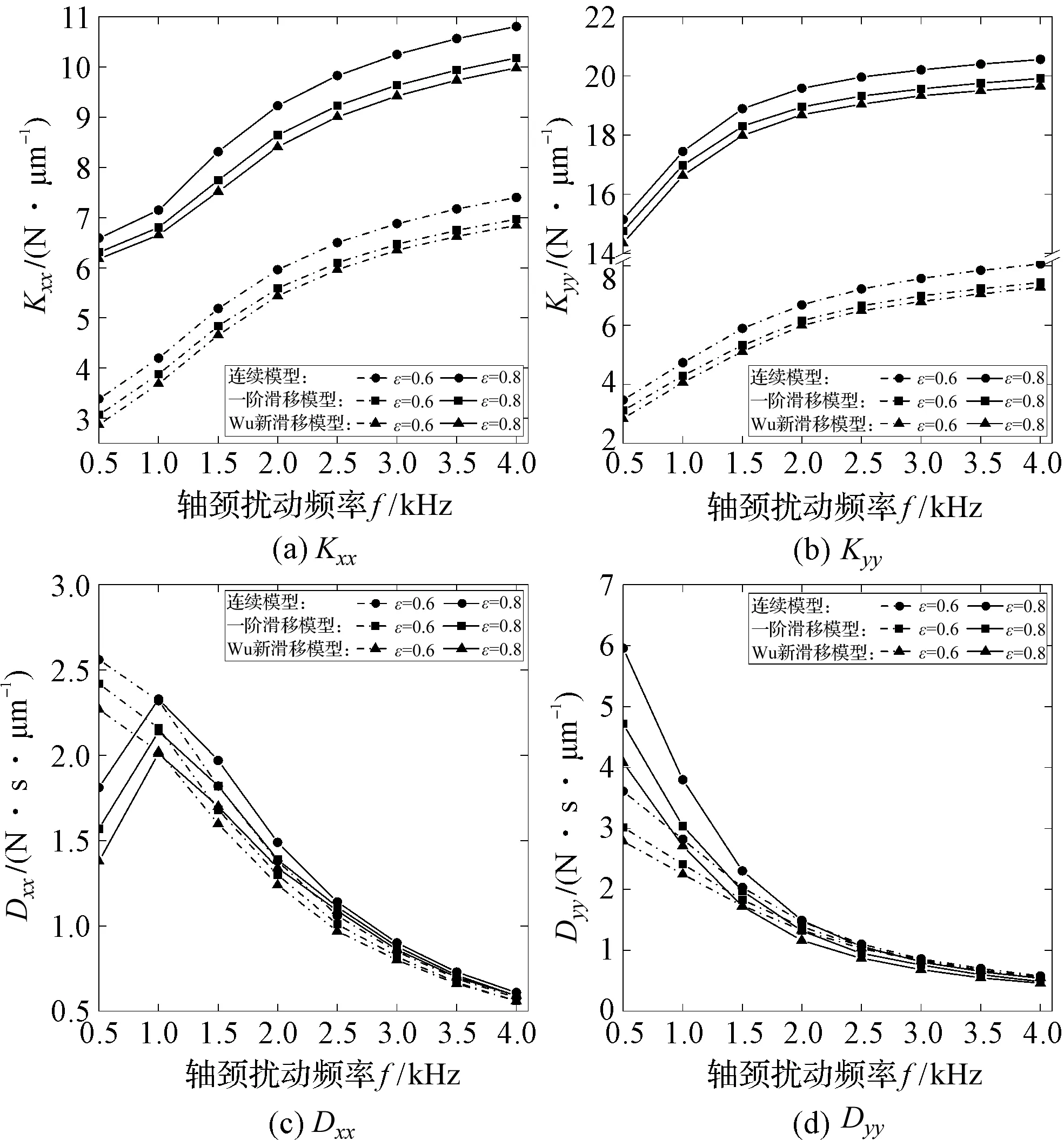
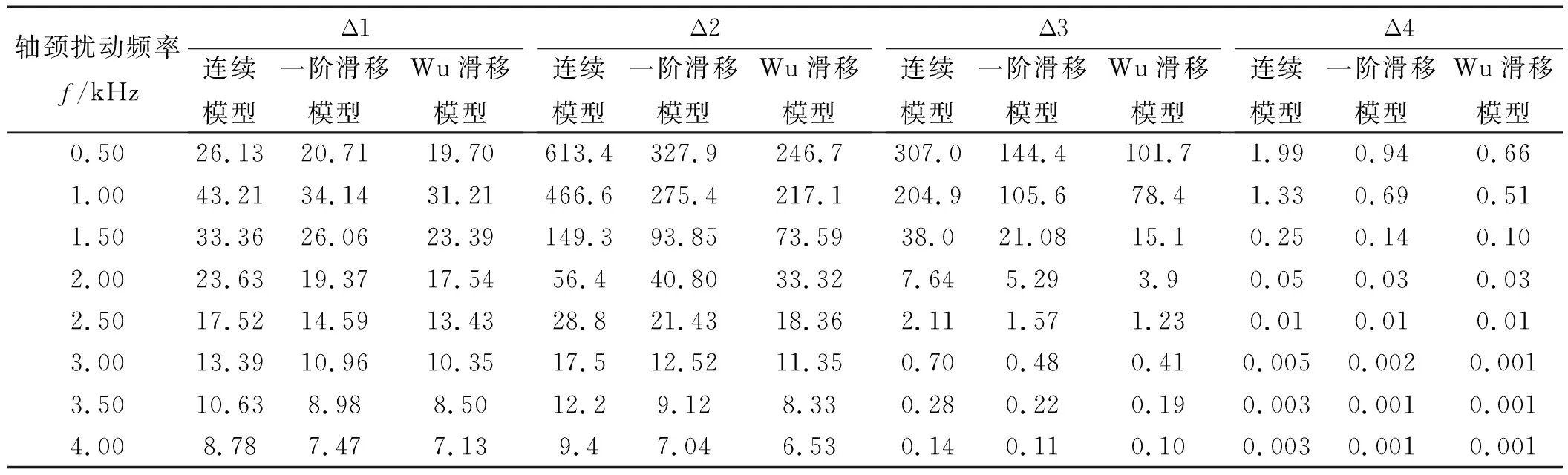
然而隨著微機電系統尺寸的不斷微型化,其關鍵支撐部件軸承間的潤滑氣膜將會變得極薄,氣體將會處于稀薄狀態,其間的氣體將會在固壁表面發生滑移,此時若采用不考慮滑移影響的傳統連續模型分析軸承轉子系統的動力學特性,將影響其準確性。因此,需考慮滑移效應下提出的修正模型對其進行動力學特性分析[3-4]。文獻[5]指出了當軸承最小氣膜間隙處的克努森數Kn值處于氣流過渡流動區域(0.1 針對以上問題,以MEMS下的微軸承為研究對象,本文推導考慮一階滑移修正及Wu新滑移修正的動力學雷諾方程,采用MATLAB編程軟件編制不同模型下用于數值計算動力學雷諾方程的程序,比較不同軸承數、偏心率、軸頸擾動頻率下連續模型、一階滑移模型和Wu新滑移模型的動力學特性系數,進而分析研究氣體滑移對微軸承動力學特性的影響規律;在此數值計算基礎上,對比分析微軸承剛性轉子系統在連續模型、一階滑移模型和Wu新滑移模型下的穩定性。 微動壓氣體軸承,依靠軸承與軸套之間充入的黏性氣體,形成楔形間隙而發生相對運動,從而自動產生氣膜壓力,實現軸承轉子的動壓懸浮。 微軸承動壓作用示意圖如圖1所示。 圖1 微軸承動壓作用示意圖ω—角速度;e—偏心距;h—軸承間隙 在定常、等溫條件下,傳統連續、一階滑移及Wu新滑移修正模型下的潤滑Reynolds方程的無量綱形式為: (1) 為方便計算,筆者將3種模型的系數做歸納處理。 模型系數如表1所示。 表1 模型系數 Kn0—參考克努森數,Kn0=C1/ph=C1/(pahmPH);C1—最小氣膜間隙,C1=6.8×10-3;α—協調系數;f—取值函數,f=min[1/Kn0,1] 結合式(1)、表1可得到在小擾動工況下修正的靜態雷諾方程,及關于PE和PΘ的修正偏微分動態雷諾方程。 修正的靜態雷諾方程為: (2) 靜態氣膜厚度為: H0=1+εcosφ (3) 無量綱靜態求解邊界條件為: (4) 關于PE修正后的動態雷諾方程為: (5) 相應的動態氣膜厚度為: HE=cosφ (6) 相應的無量綱邊界條件為: (7) 關于PΘ修正后的動態雷諾方程為: (8) 相應的動態氣膜厚度為: HΘ=sinφ (9) 相應的無量綱邊界條件為: PΘ(φ,±B/2)=0 (10) 1.3.1 靜態承載力、偏位角求解表達式 聯立式(2~4),基于MATLAB編制靜態雷諾方程有限差分程序,迭代求解可得到靜態氣膜壓力P0分布的數值解,從而得到軸承靜態承載力W和軸頸偏位角θ的求解表達式,即: (11) (12) 式中:Wn—軸頸承載力在偏心方向的分量;Wt—軸頸承載力在垂直偏心方向的分量。 1.3.2 動態剛度系數和動態阻尼系數求解表達式 根據式(5~10),基于MATLAB編制動態雷諾方程有限差分程序,通過迭代求解可得到微軸承的動態氣膜壓力PE和PΘ,從而可以得到滑移效應下,微軸承的動特性系數求解表達式: (13) 轉換式(13)中的系數代入到直角坐標系中,可求解直角坐標系下的動特性系數,即: (14) 結合文獻[8]可知,該系統的力平衡運動方程為: (15) (16) 將上述微分方程組合并,則該方程組的通解為: (x,y)=(x0,y0)est (17) 式中:s—為復頻率,s=u+iwj;u—復數的實部(阻尼);ωj—虛部(軸頸自然渦動頻率)。 聯立式(15~17),整理可得: (18) 由線性代數理論可知,式(18)有非零解的充要條件是該方程組的系數行列式為0,即: (19) 展開式(19)的2階行列式,可得到微軸承—剛性轉子系統的特征方程式: a4s4+a3s3+a2s2+a1s+a0=0 (20) (21) 根據系統穩定性Routh-Hurwitz判別準則[9]可知,只需要判斷特征值s的解是否都有負實數部,就可以判斷軸承轉子系統是否穩定。因此,通過計算式(20)中的特征值,就可預估微軸承剛性轉子系統的穩定性。 針對如圖1所示的微軸承結構,微軸承設定最終微小間隙下氣膜收斂精度為10-6。 數值仿真計算參數如表2所示。 表2 數值仿真計算參數 為進行微軸承動力學特性的數值分析[10],本文采用MATALB編程平臺編制程序,進行微軸承動力學特性的數值分析。 數值仿真流程圖如圖2所示。 圖2 數值仿真流程圖 為驗證本文用于微軸承動力學特性分析時程序的正確性,基于如圖2所示的數值仿真流程圖,筆者采用有限差分法進行數值計算,并將得到的結果與文獻[11]的數值結果進行對比。 數值仿真程序驗證圖如圖3所示。 圖3 數值仿真程序驗證圖 對比結果表明:本文程序得到的動特性系數與文獻中的數據幾乎完全一樣;使用該程序計算得到的動力學特性系數與文獻中的數據相對誤差均在3%以內,由此驗證了本文程序的準確性。 為分析微軸承的靜態特性,筆者從微軸承靜態雷諾方程出發,對比分析最小膜厚度處微軸承在3種模型下的靜態氣膜壓力分布及軸承數(描述氣體可壓縮性對動壓效應影響程度的一個壓縮系數,標量)、偏心率(描述軸頸運轉時的偏心程度,標量)分別對軸承的靜態承載力、偏位角的影響規律。 基于如表2所示的軸承結構參數,在φ=180°、偏心率0.6及軸承數為1.7時,3種模型下的氣膜壓力分布圖如圖4所示。 圖4 3種模型下的氣膜壓力分布圖 對比3種模型下的氣膜壓力分布發現:在最小氣膜厚度處,3種模型得到的氣膜壓力差異明顯,這是因為在最小氣膜厚度處,和氣體滑移效應密切相關的流體粘性剪切應力最強,致使在該區域的氣流速度分布發生變化,進而使該區域的氣壓分布發生變化;同時,可以得到連續模型預測的氣膜壓力最高,一階滑移模型次之,Wu新滑移模型預測的氣膜壓力最低。 為進一步分析微軸承的靜態特性,筆者采用數值分析方法,得到3種模型下承載力與偏心率、軸承數之間的關系,如圖5所示。 圖5 3種模型下承載力與偏心率、軸承數之間的關系 從圖5可以看出:在相同條件下,考慮氣體滑移影響時,隨著偏心率、軸承數的變化,氣體滑移影響下的承載力明顯下降,相比滑移模型預測的結果而言,連續模型預測的承載力偏大;且隨著偏心率、軸承數的增大,各模型之間的承載力偏差在逐漸變大,這是因為偏心率和軸承數的增大,直接導致了最小氣膜處的間隙變大,剪切應力增強,氣體滑移效應變得顯著,進而使最小氣膜間隙處的氣膜壓力降低,軸承的承載力下降。但連續模型并沒有考慮氣體滑移的影響,所以預測得到的承載力值相對較高。 綜合上述的分析可知,連續模型預測的承載力偏差最大、一階滑移模型次之、Wu新滑移模型最小;對比一階滑移模型和Wu新滑移模型預測的軸承氣膜壓力可知,一階滑移模型較高地預估了滑移效應下軸承的承載力。 因此,在對滑移下微軸承的動力學特性分析時,需考慮精度更高的Wu新滑移模型。 為分析氣體滑移對微軸承動態特性的影響,筆者按表2所示的軸承結構參數(氣膜收斂精度為10-6),從微軸承動態雷諾方程出發,研究了氣體滑移影響下軸頸擾動頻率、偏心率、軸承數與軸承動態剛度和動態阻尼系數的變化關系。 3種模型下,動態特性系數與偏心率之間的關系如圖6所示。 圖6 3種模型下動態特性系數與偏心率之間的關系 從圖6中可以看出: (1)在相同條件下,考慮氣體滑移的影響時,軸承的動態剛度系數,受偏心率的影響較大,軸承的動態阻尼系數,幾乎不受偏心率的影響;其中,當軸頸的擾動頻率大于2.5時,動態主阻尼系數幾乎不受偏心率的影響; (2)在相同軸頸擾動頻率下,大偏心率對應著大的動態主剛度系數和主阻尼系數,且由于只有垂直方向受外力作用,垂直方向上大偏心率對應的動態主剛度系數Kyy、主阻尼系數Dyy相對小偏心率較大。 基于靜特性數值分析計算結果,3種模型下動態特性系數與軸承數之間的關系如圖7所示。 圖7 3種模型下動態特性系數與軸承數之間的關系 從圖7中可以看出:在相同條件下,考慮氣體滑移影響時,不同軸承數下的動態主剛度系數Kxx、Kyy均隨軸頸擾動頻率的增大而增大,主阻尼系數Dxx、Dyy隨軸頸擾動頻率的增大而減小,且氣體滑移對阻尼系數的影響也在逐漸減弱;大的軸承數對應著大的動態主剛度系數、小的動態主阻尼系數,這主要是因為,大轉速意味著高氣膜壓力,會使相對應的軸承軸頸位置發生變化,軸承的動態主剛度隨著轉速的增加而變大,相對應的動態主阻尼系數隨之變小。 由圖(6,7)可知,在氣體滑移影響下,不同軸承數、偏心率對應的動特性系數均有所下降,且Wu新滑移模型計算的值遠低于連續模型和一階滑移模型,這主要是因為氣體滑移會使潤滑氣體的速度有所降低,進而氣膜壓力降低,從而導致軸承動特性系數減小。 在偏心率為0.6、軸承數為1.7時,結合3種模型下的動特性系數與軸承轉子系統穩定性判別理論,可求得各擾動頻率下特征值對應的所有子行列式的值,判斷在該擾動頻率下是否滿足穩定性條件,為軸承穩定性設計提供理論依據。 在相應擾動頻率下,3種模型各子階行列式的值如表3所示。 表3 在相應擾動頻率下3種模型各子階行列式的值 從表3可知,3種模型在各擾動頻率下的各子行列式的值都為正數,且Wu新滑移模型計算的值相比連續模型、一階滑移模型低;即在軸承數為1.7的情況下,微軸承剛性轉子在相應擾動頻率范圍內是穩定的,且連續模型較高地估計了轉子系統的穩定性。 針對微機電系統下傳統連續模型無法準確描述氣體滑移對微軸承動力學特性影響規律的問題,筆者推導了考慮一階滑移修正及Wu新滑移修正的動力學雷諾方程,比較了不同軸承數、偏心率、軸頸擾動頻率下連續模型、一階滑移模型和Wu新滑移模型的動力學特性系數,進而研究了氣體滑移對微軸承動力學特性的影響規律;在此數值計算基礎上,筆者對比分析了微軸承剛性轉子系統在連續模型、一階滑移模型和Wu新滑移模型下的穩定性。 研究結果可知,氣體滑移下軸承的動力學特性與軸承的軸承數、偏心率及軸頸擾動頻率密切相關,在微小氣膜間隙、高轉速工況下,不考慮氣體滑移影響的連續模型較高地估計了軸承剛性轉子系統的穩定性,且Wu滑移模型下得到的值最小。 綜上所述,結合物理理論依據和微小間隙下氣體滑移的影響,在設計微機電系統下的微軸承時,為得到氣體滑移下更準確的軸承設計參數,應使用Wu新滑移模型對傳統連續模型下的動力學雷諾方程進行滑移修正。 為計算方便,筆者使用的MEMS下的微軸承結構較為簡單。在今后的研究中,筆者將會引入更復雜的微軸承結構,來驗證分析該理論的適用性;同時,考慮使用數值仿真與試驗相結合的方法,筆者在不同的算例條件下,分析氣體滑移對微軸承動力學特性的影響,為設計更優的MEMS下微軸承提供幫助。1 滑移修正下的動力學方程
1.1 微軸承的滑移修正雷諾方程
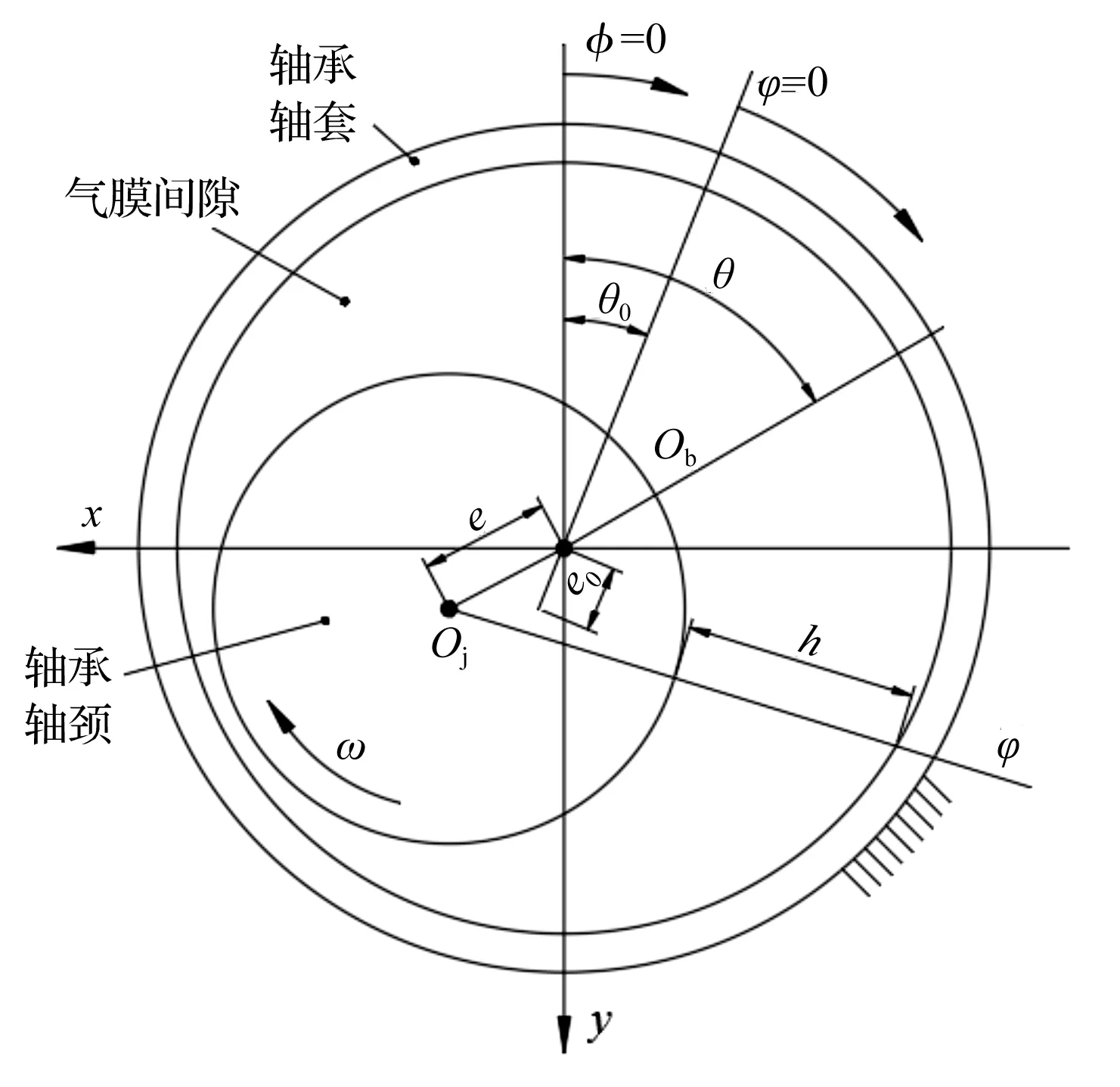
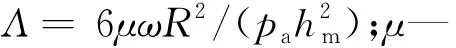

1.2 滑移修正下的靜、動態雷諾方程
1.3 動力學特性系數求解表達式
2 微軸承轉子系統穩定分析方法
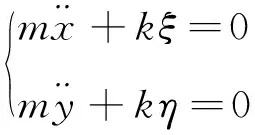
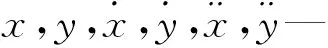
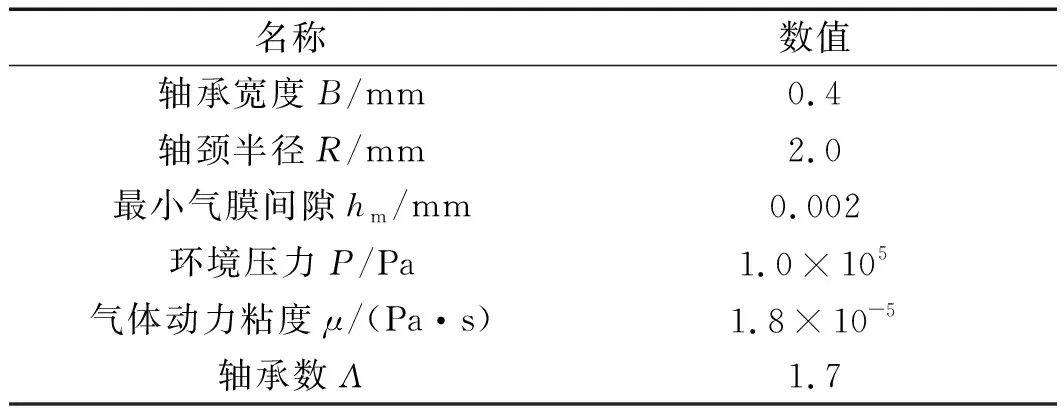
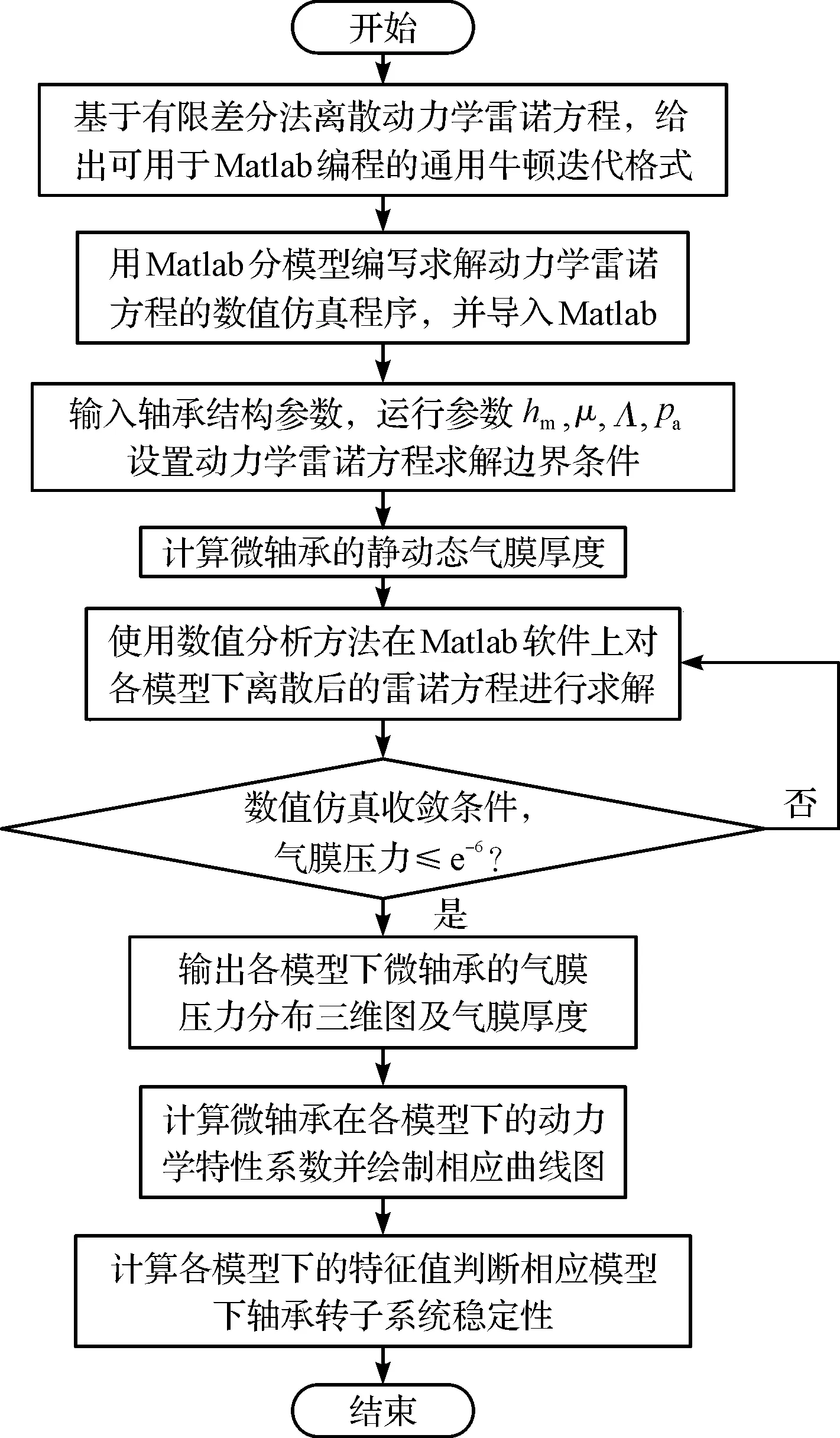
3 數值仿真實驗及結果分析
3.1 數值仿真程序驗證
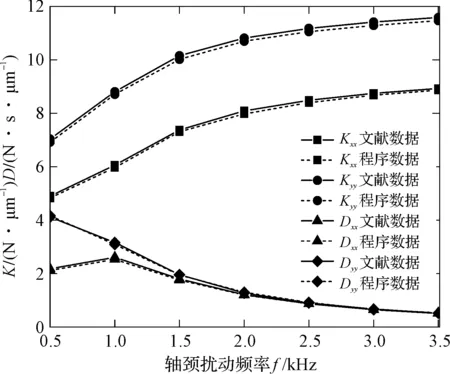
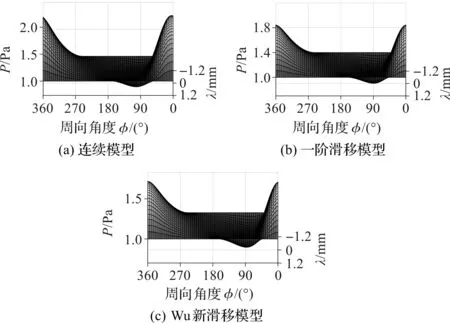
3.2 靜特性系數數值仿真結果分析
3.3 動態特性系數數值仿真結果分析
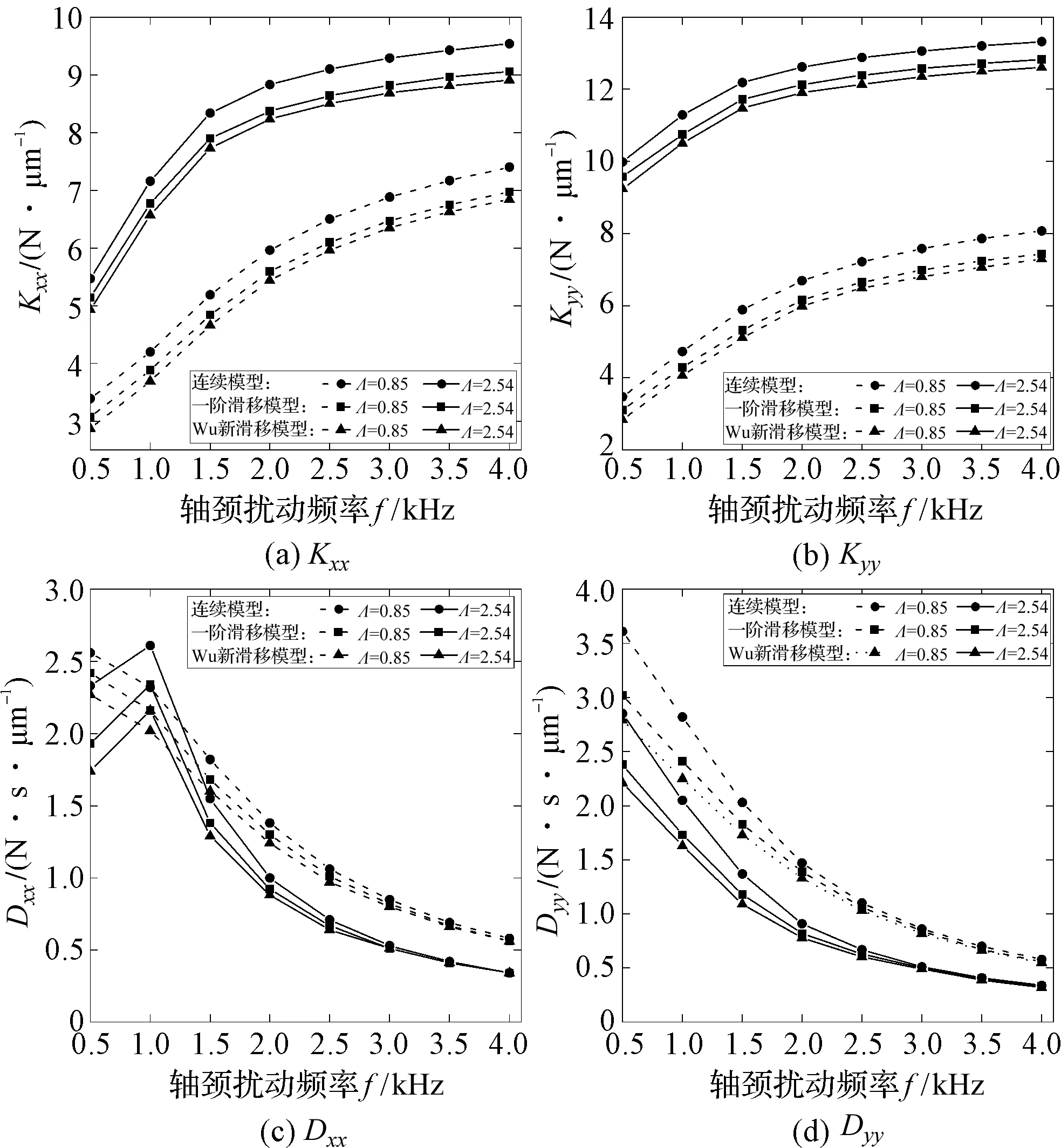
4 微軸承轉子系統穩定性分析
5 結束語

