基于分形理論的菱鎂礦粉磨程度表征研究

羅奔， 李闖*,2,3， 楊云川

1.沈陽理工大學 材料科學與工程學院，遼寧 沈陽 110159； 2. 礦物加工科學與技術國家重點試驗室，北京 102628； 3. 東北大學 資源與土木工程學院，遼寧 沈陽 110004

1 引言

菱鎂礦是一種碳酸鎂礦物，用途十分廣泛。因其中的氧化鎂具有較強的耐火性、黏結性及其他優良物化特性，被廣泛應用于耐火材料的制備；還可以利用菱鎂礦提煉金屬鎂，在冶金、化工、建材及醫療等領域也發揮著巨大的作用[1]。

中國菱鎂礦產量及出口量均居世界首位，是我國的優勢礦產資源之一[2]。雖然我國菱鎂礦儲量豐富，但由于近年來采富棄貧的采集方式，使得我國優質菱鎂礦資源開發殆盡，而低品位菱鎂礦不能直接用于生產高級材料，因此需通過選礦來實現對低品位菱鎂礦的合理利用。而在選礦過程中，選擇合適的磨礦細度有助于使目的礦物與脈石礦物有效分離，對浮選過程十分有利[3]。郗悅等[4]以遼寧海城地區的菱鎂礦為原料，在反浮選試驗研究里指出磨礦細度在-0.074 mm含量為85%時為最佳條件；董慶國等[5]在遼寧某低品位菱鎂礦浮選除雜試驗研究中發現當磨礦細度在-0.074 mm含量為85%時回收率達到最大值。

但上述研究中對于菱鎂礦粉磨程度的表征仍是定性分析，因為對于具有不規則形貌的顆粒破碎材料，傳統歐式幾何理論無法實現對其的定量描述，而分形理論作為二十世紀非線性科學研究的重要成果，可以用于解決這一問題。

分形理論在20世紀70年代由Mandelbort[6]在針對海岸線長度的闡述中首次提出，近50年來，分形理論被廣泛應用于信息、數學、材料、藝術等領域，成為人們研究非線性科學的重要工具[7-10]。

自然界中的分形分為有規分形和無規分形，研究表明，破碎顆粒材料大多滿足自相似，屬于無規分形，顆粒粒度分布可用分形維數表征[11-13]。對于礦物破碎材料研究領域，謝和平等[14]在試驗中發現分形維數可以直觀地定量反映巖石破碎的程度；焦紅蕾等[15]利用分形理論建立顆粒數分布模型、顆粒表面積分布模型和顆粒質量分布模型來表征煤炭研磨顆粒粒度分布。但運用分形理論來表征菱鎂礦粉磨程度的研究尚未見報道。

本文以菱鎂礦為原料制備不同磨礦細度的菱鎂礦粉體，通過激光粒度儀測量其粒度分布，結合分形維數定義，以MATLAB軟件為平臺，探究如何實現菱鎂礦粉磨程度的定量表征，探尋體分形維數與磨礦細度的關系。為優化低品位菱鎂礦浮選結果提供一個新思路。

2 實 驗

2.1 樣品制備

本文選用來自遼寧省丹東地區的天然菱鎂礦，其主要化學成分分析結果見表1。

表1原礦化學成分分析

Table1 Analysis of raw ore chemical composition

ComponentMgOCaOSiO2TFegrade/%45.21.093.180.34

將原料經顎式破碎機、圓錐破碎機兩段破碎后過篩，按照磨礦質量濃度67%稱取200 g礦樣與98.5 g水混合，加入球磨機濕磨，通過調整磨礦時間，得到磨礦時間與磨礦細度的關系，如圖1所示。

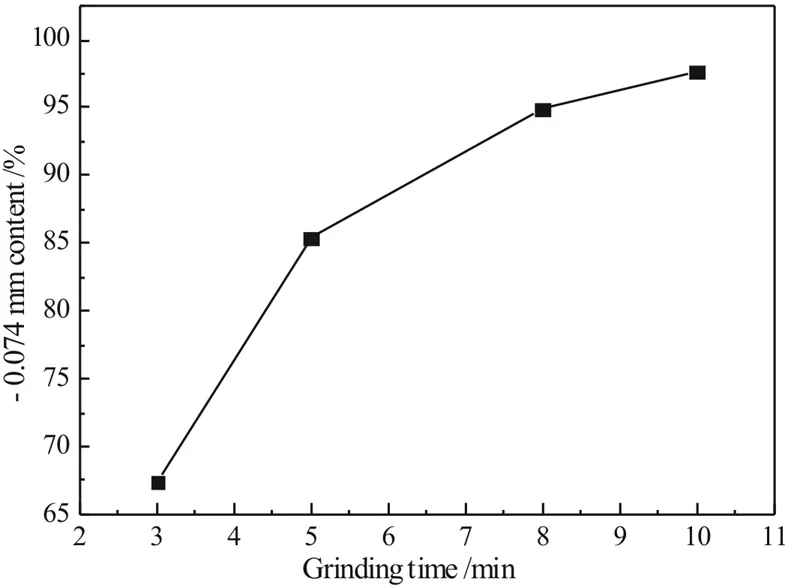
圖1磨礦時間與磨礦細度關系曲線

Fig. 1 Relationship between grinding time and grinding fineness

為探尋分形維數與磨礦細度的關系，需制備不同磨礦樣品，本文選取5個時間點，分別制備磨礦細度為73.8%、77.5%、81.6%、88.8%、94.2%的菱鎂礦粉體各500 g，裝袋備用。

2.2 粒度檢測試驗

利用五點取樣法取制備好的礦樣1 g，與100 mL去離子水配置濃度為1%的溶液，將其加入BT-9300S型激光粒度儀，超聲3 min后開始測量，采用配套的軟件記錄測試結果，導出顆粒粒度檢測報告。

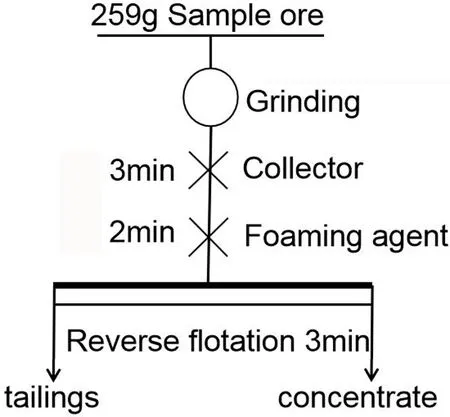
圖2磨礦細度試驗流程圖

Fig. 2 Flowsheet of grinding fineness test

2.3 不同磨礦細度的選別試驗

取250 g制備好的礦樣，按照2#油用量20 g/t，捕收劑十二胺用量150 g/t的試驗條件，利用單槽浮選機進行除硅反浮選。磨礦細度試驗流程如圖2所示。

2.4 試驗儀器及方法

粒度檢測試驗設備采用丹東百特儀器有限公司的BT-9300S型激光粒度儀，其粒徑測定范圍為0.1 μm～340 μm，重復性誤差和準確性誤差均小于1%(標樣D50偏差)。首先進行參數設置，設置測試樣品的介質和遮光率；然后進行背景測試，消除管道中氣泡，進行光路校正，減小試驗誤差；將配置的溶液加入，經超聲分散后進行測量，采用配套的軟件記錄測試結果，導出檢測報告。結合分形維數定義，以MATLAB軟件編程，可求出用于描述粉磨菱鎂礦粒度分布特征的體分形維數和特征粒徑。

3 粉磨菱鎂礦粒度分布特征

3.1 粉磨菱鎂礦粒度分布分形維數研究

大量研究表明，礦物破碎材料粒徑分布是十分復雜的，這些粒徑不一的顆粒形貌不規則、呈無序分布，使用傳統歐氏幾何無法實現對其的定量表征，但由于其滿足分形理論的自相似性，從而可以利用分形理論探討其粒度分布特征。

(1)體分形維數計算數學模型

Rosin-Rammler分布形式通常通過負累計率的形式表征，其數學表達式如下：

(1)

式中：y-為粒徑大于x的菱鎂礦質量負累積率，x為特征粒徑，xe為分布模數；m為便于建立分形維數測定數學模型，以下描述選取Rosin-Rammler分布的正累積率表達形式。

本文應用Yang[17]提出的體分形維數測定方法。假設一個單位長度的特征粒徑為R=xe/x，其與分形特征粒徑的關系為：

(2)

式中：D3為體分形維數。

菱鎂礦質量正累計率y+對于R的導數與y+成正比，與RF成反比，其微分形式為：

(3)

式中C1=kC2，對(3)式積分可得：

(4)

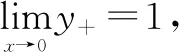
(5)

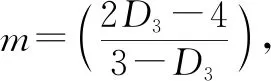
(2)體分形維數計算

根據粒度檢測報告，由上述體分形維數計算數學模型，可計算出不同細度下菱鎂礦樣品的特征參數。計算結果見表2。

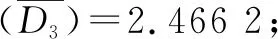
表2不同細度下菱鎂礦粒度分布特征擬合結果 /%

Table2 Fitting results of particle size distribution characteristic of magnesite at different fineness fineness

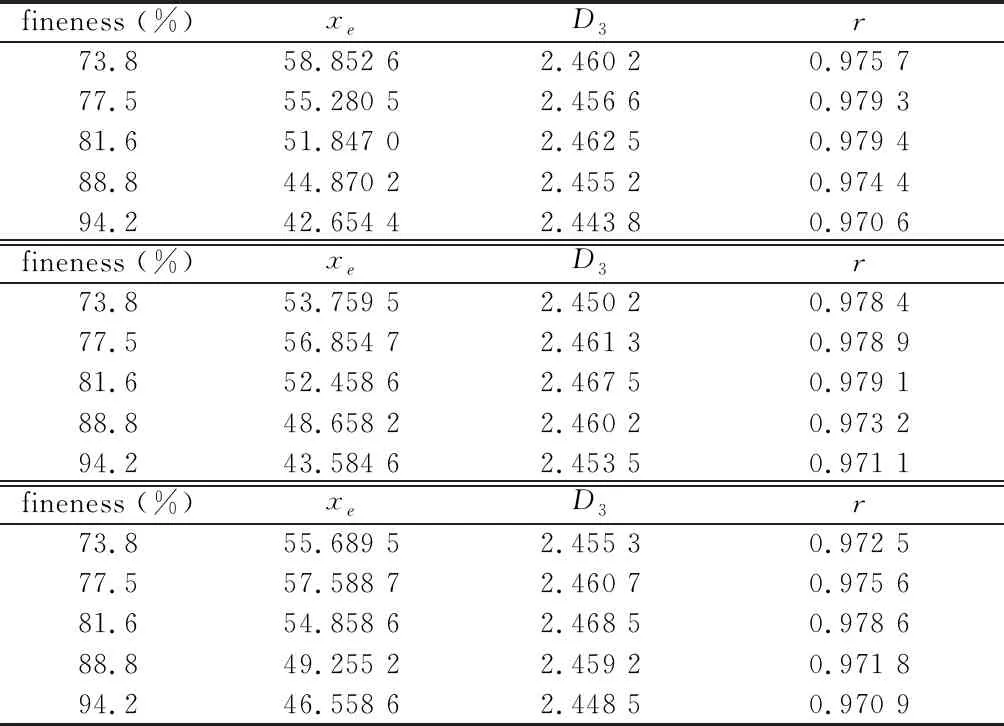
fineness (%)xeD3r73.858.852 62.460 20.975 777.555.280 52.456 60.979 381.651.847 02.462 50.979 488.844.870 22.455 20.974 494.242.654 42.443 80.970 6fineness (%)xeD3r73.853.759 52.450 20.978 477.556.854 72.461 30.978 981.652.458 62.467 50.979 188.848.658 22.460 20.973 294.243.584 62.453 50.971 1fineness (%)xeD3r73.855.689 52.455 30.972 577.557.588 72.460 70.975 681.654.858 62.468 50.978 688.849.255 22.459 20.971 894.246.558 62.448 50.970 9

圖3是不同磨礦細度下菱鎂礦相對質量負累計規律。可以看出，菱鎂礦粒徑與相對質量負累積率是一條“S”型曲線，符合Rosin-Rammler分布規律，且擬合曲線與試驗曲線十分接近，只在中粒徑附近存在一定的偏差，但相關系數都在97%以上；這說明粉磨菱鎂礦顆粒質量分布滿足統計意義上的自相似性，可以用分形維數來定量表征。

4 體分形維數與磨礦細度關系驗證

4.1 磨礦細度試驗結果

將浮選試驗得到的精、尾礦烘干取樣，經化學成分分析可得到不同磨礦細度下菱鎂礦精礦產率、MgO品位、MgO回收率，結果如表3和圖4所示。

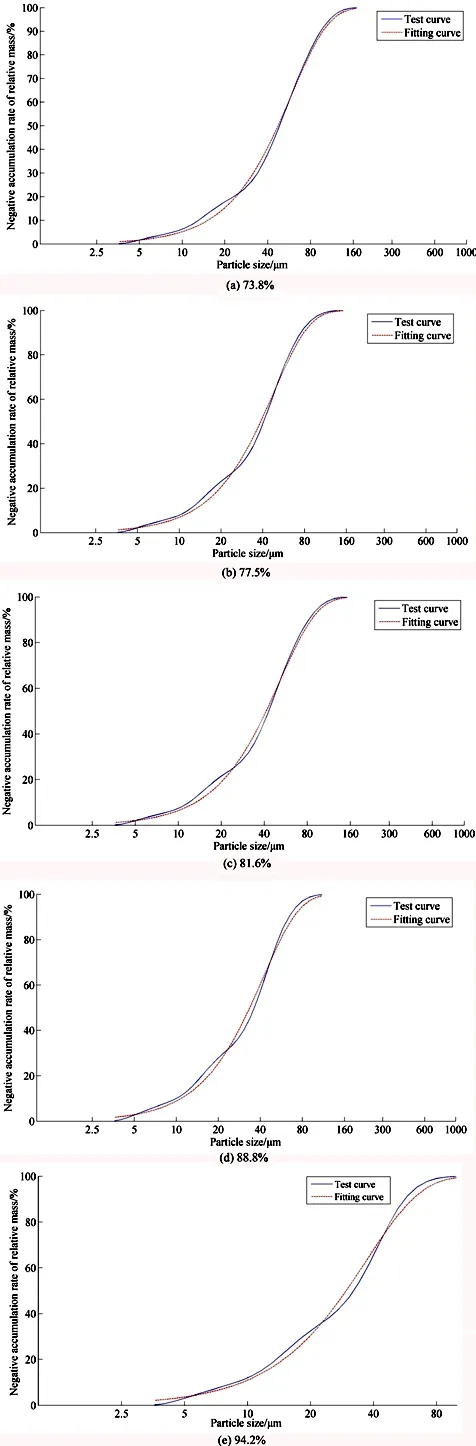
圖3不同磨礦細度下菱鎂礦相對質量負累積規律

Fig. 3 Negative accumulation of relative mass of magnesite at different grinding fineness

由圖4可知，共進行3組選別試驗，每組分別為5個不同細度，共計15次試驗。發現隨著磨礦細度的增加，精礦中MgO品位大體呈先增長后減小的趨勢，且MgO回收率也是先升高后降低，當磨礦細度為81.6%時，MgO品位、回收率達到最高。經綜合考慮，確定試驗最佳菱鎂礦浮選條件為磨礦細度為-0.074mm含量81.6%。

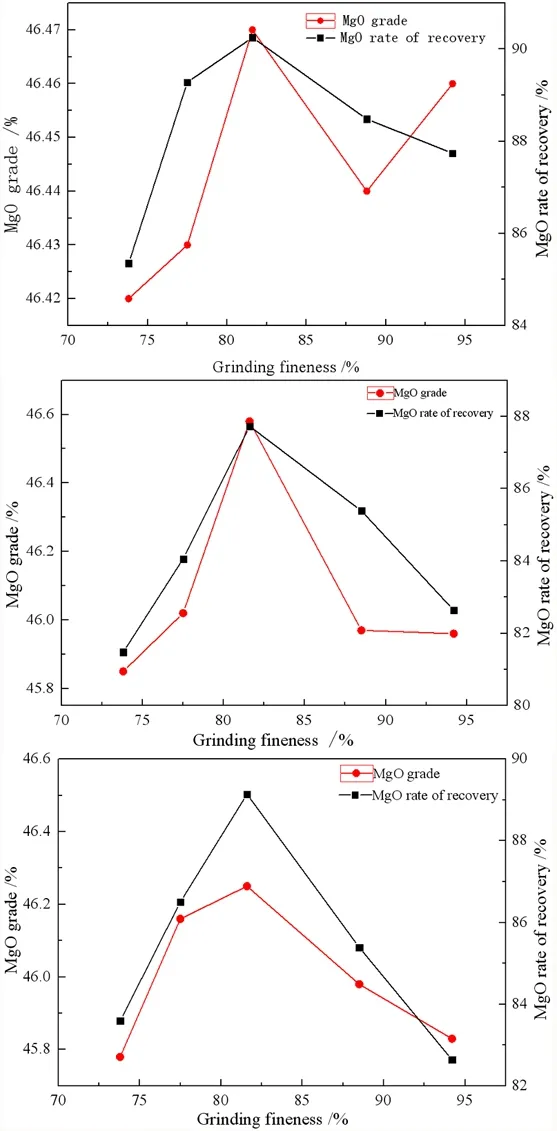
圖4磨礦細度試驗結果

Fig. 4 Results of grinding fineness test

表3磨礦細度試驗結果

Table3 Results of grinding fineness test

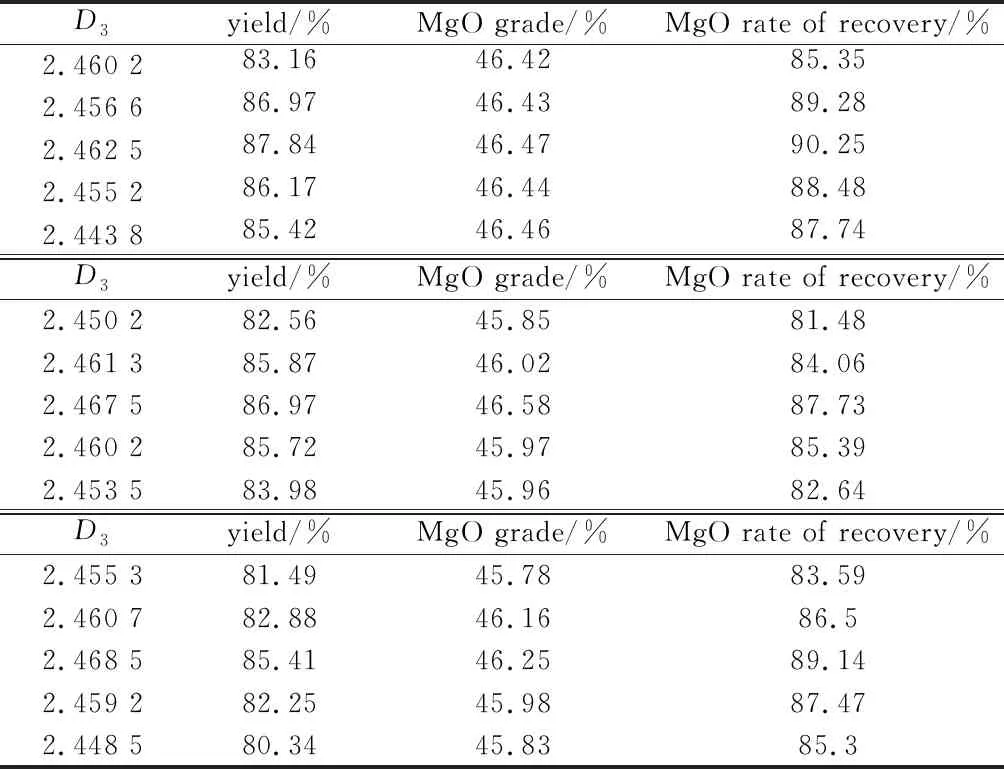
D3yield/%MgO grade/%MgO rate of recovery/%2.460 283.1646.4285.352.456 686.9746.4389.282.462 587.8446.4790.252.455 286.1746.4488.482.443 885.4246.4687.74D3yield/%MgO grade/%MgO rate of recovery/%2.450 282.5645.8581.482.461 385.8746.0284.062.467 586.9746.5887.732.460 285.7245.9785.392.453 583.9845.9682.64D3yield/%MgO grade/%MgO rate of recovery/%2.455 381.4945.7883.592.460 782.8846.1686.52.468 585.4146.2589.142.459 282.2545.9887.472.448 580.3445.8385.3

4.2 體分形維數與磨礦細度關系驗證

綜上所述，體分形維數與磨礦細度關系如圖5所示。

由圖5可知，當體分形維數最大時，所對應的磨礦細度為-0.074 mm含量81.6%。說明在3次試驗中，當體分形維數處于極大值時，菱鎂礦磨礦細度也為最佳條件，證明了粉磨菱鎂礦的粉磨程度通過體分形維數來進行定量表征是合理的。

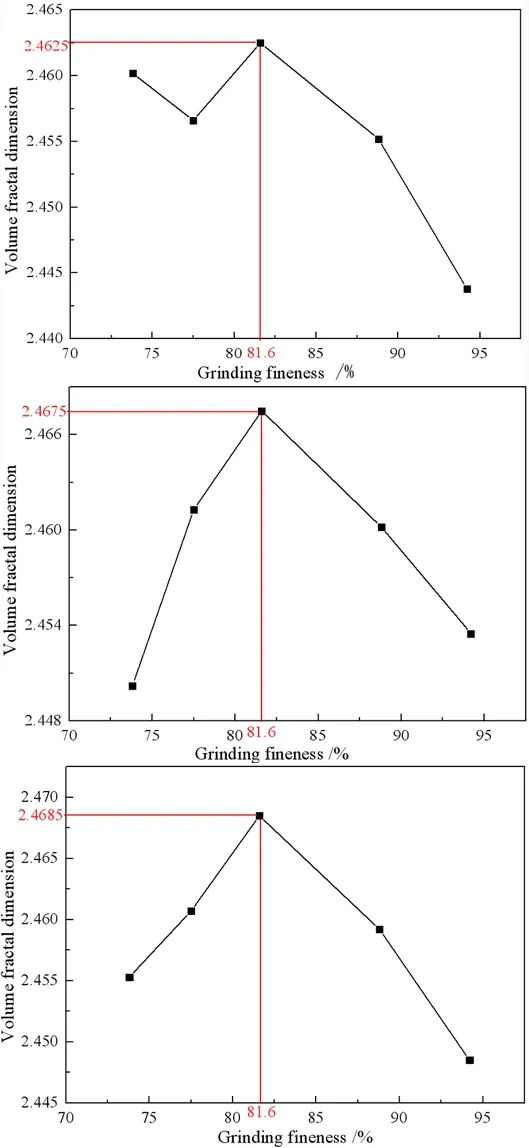
圖5體分形維數與磨礦細度關系圖

Fig. 5 Relationship between volume fractal dimension and grinding fineness

5 結論

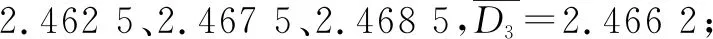
(2)本文選取5個不同磨礦細度作為變量，通過3組選別試驗發現磨礦細度為-0.074 mm含量81.6%時，浮選效果較好。

(3)本文研究了體分形維數與磨礦細度關系，結果表明：當體分形維數達到極大值時，其對應的菱鎂礦磨礦細度浮選效果較好，證明了菱鎂礦的粉磨程度可以通過體分形維數來進行定量表征。為描述菱鎂礦粉磨程度提供了一個新的表征手段，建立了體分形維數與選礦浮選的聯系。