D + DBr反應的態-態動力學研究

袁方園 朱子亮

(濰坊科技學院通識學院， 壽光 262700)

(2020 年3 月2日收到; 2020 年4 月2日收到修改稿)

在0—2.0 eV的碰撞能范圍內采用含時量子波包方法和二階分裂算符傳播子對初始量子態為(v0 = 0， j0 = 0)的D + DBr反應進行了態分辨理論水平上的動力學計算. 計算了抽取反應通道D + DBr → Br + D2和置換反應通道 D′+DBr→D+D′Br 的反應概率、積分截面、微分截面、產物的振動和轉動分布以及速率常數等動力學性質， 并與相應的理論和實驗結果進行了比較. 結果表明: 計算的速率常數與實驗結果十分符合. 微分截面的結果表明: 對于抽取反應， 前向的剝離反應機制在反應過程中占據主導地位; 對于置換反應， 頭碰頭的反彈機制占據主導地位.

1 引 言

氫原子和鹵化氫的反應在發展和理解基礎的化學反應上有著重要意義， 因此其抽取和置換反應在最近幾十年當中受到了廣泛的關注. 對于H + HBr及其同位素反應， 大量的實驗工作集中在測量該體系的熱速率常數、同位素效應、積分截面、以及產物的振動和轉動電子態分布等動力學信息[1-10].1989年， Aker等[7，8]采用連貫的反斯托克斯拉曼散射光譜測量了1.6 eV能量下H + HBr反應抽取和置換反應通道的積分截面和產物的振動和轉動態分布. 1990年， Umemoto等[6]采用一種脈沖輻射共振吸附技術在214—300 K的溫度范圍內測量了H + HBr及其同位素反應的速率常數. 采用激光閃光光解HBr分子和連續波共振熒光檢測H原子方法， Seakins和Pilling[3]與Talukdar等[4]也分別測量了H + HBr反應不同溫度范圍的速率常數.

在理論方面， H + HBr反應的勢能面構建也在最近的幾十年中有了極大的進展. 基于多參考組態相互作用方法(MRCI)計算的104個從頭算能量點， Lynch等[11]構建了第一個extended London-Eyring-Polanyi-Sato (eLEPS)函數形式的從頭算勢能面. 然而基于該勢能面得到的速率常數往往低于實驗值并且100多個能量點也不足以描述復雜的勢能面地貌. 2003年， Kurosaki和Tayanagi[12]采用MRCI方法和AVTZ基組構建了BrH2體系基態和兩個激發態的勢能面， 并且在基態的勢能面上考慮了自旋軌道耦合修正(MB1). 然而基于MB1勢能面的速率常數明顯大于實驗值. 不久之后， 他們又對MB1勢能面進行了修正， 降低了約0.3 kcal/mol的勢壘高度， 并將新的勢能面命名為MB2[13]. 之后又在MB2勢能面的基礎上修改了Br + H2漸進區T型結構的勢阱， 并命名為MB3.Kurosaki和Tayanagi[12]的勢能面得到了廣泛的應用. Quan等[14-16]采用MB1， MB2和MB3勢能面和含時量子波包方法進行了一系列的動力學計算并報道了反應概率、積分截面和速率常數等物理量. 結果表明對于H + HBr反應， MB3勢能面明顯優于MB1和MB2勢能面， 基于MB3勢能面的速率常數和實驗結果十分吻合. Fu和Zhang[17]和Fu等[18]也采用MB3勢能面和含時量子波包方法進行了動力學計算， 并報道了量子態分辨的積分和微分截面. 然而， Fu和Zhang[17]基于MB3勢能面得到的速率常數明顯大于實驗值. 這與Quan等[14-16]得到的結果有很大的差異.

2011年， Jiang等[19]構建了H + HBr反應的一個新的勢能面. 采用MRCI方法進行了從頭算計算， 在計算中考慮了自旋軌道耦合修正并把基組外推到了完全基組極限. 此外， 基于新構建的勢能面， Jiang等[19]采用含時量子波包方法進行了動力學計算. 結果表明基于該勢能面得到的速率常數與實驗結果十分吻合. 之后， Xie等[20]采用該勢能面進行了H + HBr反應的態-態動力學計算， 報道了反應概率、積分截面、微分截面、產物的振動和轉動態分布等動力學信息， 并與相應的實驗結果進行了對比. 結果表明， 基于該勢能面得到的產物振動和轉動態分布與實驗值存在較大差距. 同年，Jiang等[21]又構建了關于BrH2體系的透熱勢能面并計算了Br(2p3/2，2p1/2) + H2反應的積分截面.2012年， Xie等[22]采用Jiang等[21]構建的透熱勢能面在量子態分辨的理論水平上計算了Br(2p1/2) +H2反應的猝滅過程. 2012年Zhang等[23]也構建了BrH2體系的透熱勢能面并與Jiang等[21]的透熱勢能面進行了比較， 同時對D + DBr反應進行了動力學計算， 報道了積分截面和速率常數等動力學信息. 2014年， Zhang等[24]采用他們構建的透熱勢能面進行了H + HBr反應體系的同位素計算. 將得到速率常數與實驗結果進行了對比， 發現理論結果與實驗結果有或高或低的偏差. 最近的勢能面是由Li等[25]在2019年構建的， 在從頭算計算中采用MRCI方法、AVTZ和AVQZ基組計算了約63000個從頭算能量點， 并采用神經網絡方法對勢能面進行了擬合. 勢能面的構建過程中， 考慮了自旋軌道耦合修正并將基組外推到了完全基組極限. 此外， 基于新構建的勢能面， Li等[25]采用含時量子波包方法進行了H + HBr反應的動力學計算. 得到的抽取通道的產物振轉態分布以及速率常數都與實驗結果十分符合.

綜上， 之前的理論研究大部分集中在H + HBr反應上， 對于同位素的理論研究相對較少. 據我們所知， 到目前為止還沒有關于其同位素反應在量子態分辨理論層次上的研究. 基于Li等的勢能面， 本文采用含時量子波包法和二階分裂算符傳播子對D + DBr反應進行初態為(v0= 0， j0= 0)的動力學計算.

2 理論方法

含時量子波包方法在計算原子與雙原子的反應散射以及包含多原子的散射計算中有著廣泛的應用[26-30]. 這里， 僅簡單的介紹一下原子與雙原子分子反應散射的動力學方法. 在空間坐標系下， 采用反應物坐標， 對于給定的總角動量J， D + DBr反應體系的哈密頓量可以寫為

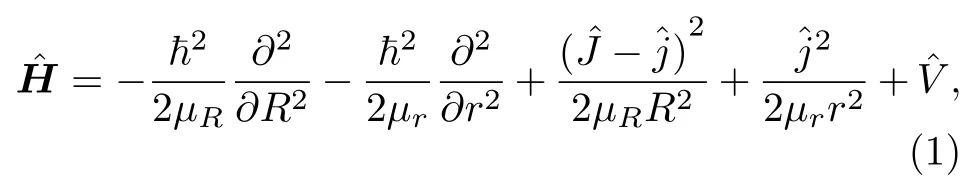
在進行動力學計算之前， 具有確定初始振動和轉動量子態的初始波包需要提前構建. 初始的含時波包是由體坐標系下的平動、振動和轉動基矢構成， 初始含時波包可以寫為

其中， 下標n為平動基矢，? 是體系的宇稱，(υ0j0K0)是體系的初始量子態， M是總角動量在空間坐標系下在z軸的投影.

在傳播過程中， 二階分裂算符[31]進行初始波包的傳播. 假設t時刻的波函數為 ψ (R，r，t) ， 那么經 過時間步長 Δt， 波函數變為 ψ(R，r，t+Δt)

在計算中， 采用快速傅里葉變換[32]計算徑向動能算符， 在離散變量表象[33]里計算勢能算符. 此外， 為了滿足邊界條件， 在邊界處設置一個吸收勢，其形式為

最終， 通過反應物坐標變換方法(RCB)[34，35]來提取態-態散射信息. 利用態-態散射矩陣可以得到反應概率、積分截面和微分截面等動力學信息.

其 中 ψ (E) 是 通 過 ψ (t) 的 快 速 傅 里 葉 變 換 得 到，是 散 射 矩 陣，是 轉 動 矩陣，? 是散射角.

指定初始量子態的速率常數是通過熱平均積分 截面的平動能得到， 其公式為

其 中 kB是玻爾茲曼常數.

3 結果和討論

本文的動力學計算是基于2019年Li等[25]報道的勢能面. 圖1給出了D + DBr反應抽取反應通道和置換反應通道的最小能量路徑. 由圖1可知， 在抽取反應通道入口處有一個微小的勢壘， 其高度約為1.54 kcal/mol. 該反應是一個放熱反應，其放熱能約為18.77 kcal/mol， 并且在反應路徑上沒有明顯的勢阱. 對于置換反應通道， 在反應路徑上有一個高度為12.14 kcal/mol的勢壘.

在進行動力學計算之前需要對計算參數進行調試. 本文測試了不同參數J = 0的反應概率， 并最終得到了最優的收斂參數. 計算中使用的參數如下:

投影截面位置 R =12.0 ;

總角動量J在z軸投影數目 Kmax=9 ;

總的傳播時間 Ttot=13000 ;

傳播時間步長 Tstep=10 .

圖 1 勢能面的最小能量路徑 (a) 抽取反應通道; (b) 置換反應通道Fig. 1. Minimum energy path of the potential energy surface: (a) Abstraction channel; (b) exchange channel.

3.1 反應概率

在0—2.0 eV的碰撞能范圍內， 總角動量J =0， 20， 40， 60， 80， 90的反應概率見圖2. 通過Li等[25]的勢能面可知， 對于抽取反應和置換反應對應的勢壘高度分別為1.54 kcal/mol (約0.067 eV)和12.14 kcal/mol (約0.525 eV). 由圖2可知， 對于抽取反應， 其閾值接近為0; 對于置換反應， 其閾值約為0.47 eV; 明顯低于勢能面上的勢壘高度， 這是由于無論是抽取反應還是置換反應都發生了隧穿效應， 從而降低了反應閾值. 對于抽取反應， 所有J的反應概率的外形都很類似. 都是先快速升高當峰值接近0.1左右之后隨著碰撞能的升高反應概率降低. 這是因為當能量較低的時候只能通過隧穿效應發生反應， 隨著能量升高， 隧穿效率增加反應概率增高. 而當碰撞能大于勢壘高度， 巨大的放熱能使得D原子的速度變快， DBr分子來不及與D原子形成化學鍵. 因此， 當碰撞能升高時， 反應概率反而降低， 這也是放熱反應的典型特征. 對于置換反應， 反應概率隨著碰撞能的升高而增高， 計算的最大J = 90， 由圖2可知， 在研究的碰撞能范圍內所有的結果都是收斂的. 然而， 對于抽取反應只有在碰撞能低于1.2 eV時， 得到積分截面和微分截面的結果才是收斂的.

圖 2 若干總角動量J的反應概率 (a) 抽取反應; (b) 置換反應Fig. 2. The reaction probabilities of several selected total angular momentum J: (a) Abstraction reaction; (b) exchange reaction.

3.2 積分截面

抽取反應的總積分截面和振動態分辨的積分截面分別列入圖3(a)和圖3(b). 為了與其他理論結果比較， Zhang等[24]的結果也列入到了圖3(a).如圖3(a)所示， 本文的結果與Zhang等[24]的結果十分符合尤其是當碰撞能比較低的時候， 然而隨著碰撞能的增加， 本文的結果與Zhang等[24]的結果差距逐漸變大. 這可能是由于計算中使用了不同的勢能面. 本文采用的是2019年Li等[25]最新報道的絕熱勢能面， 該勢能面沒有考慮不同電子態之間的非絕熱效應. 而Zhang等[24]結果是基于他們自己構建的非絕熱勢能面. 我們認為高能部分的差距是由于非絕熱效應引起的. 圖3(b)列入了積分截面的振動分辨， 發現了一個有趣的現象， 當碰撞能低于0.45 eV時， 出現了振動粒子數反轉的現象.產物D2的分布主要集中在v' = 1上. 隨著碰撞能的升高， 反轉現象變得不明顯進而消失. 這種反轉分布符合Polanyi的規則[36，37]. 隨著碰撞能的升高，其他振動激發態的通道逐漸打開. 盡管如此， D2分子的振動態分布主要還是集中在基態和第一激發態上.

圖 3 (a) 抽取反應總積分截面和文獻[24]的結果比較;(b) 抽取反應振動分辨的積分截面Fig. 3. (a) Comparison between present total integral cross section of abstraction reaction and the values obtained from Ref. [24]; (b) the vibrational state-resolved integral cross section of abstraction reaction.

圖 4 在若干選擇的碰撞能下， 產物D2的振轉態分布Fig. 4. The ro-vibrational distribution of D2 at several selected collision energies.

圖4 給出了抽取反應在碰撞能為0.4， 0.6，0.8和1.0 eV時產物的振轉態分布. 由圖4可知，隨著碰撞能的升高， 振動電子態的數目和轉動量子數的數目都增加. 這反映了隨著碰撞能的升高會有更多的碰撞能轉化為內能. 此外， 還可以看出越高的振動態具有越少的轉動量子數， 這是因為當總能固定的情況下， 內部的轉動能量轉化為振動能量.我們還發現隨著碰撞能的升高， 出現了共振峰結構. 例如， 當0.4 eV時， v' = 1是單峰結構， 0.6 eV時變為雙峰， 0.8 eV時變為三峰， 1.0 eV時變為多峰結構. 在圖1， 抽取反應的最小能量路徑上沒有發現明顯的勢阱. 本文認為， 盡管最小能量路徑上沒有勢阱， 然而當產物D2分子處于振動激發態的時候， 就會形成勢阱， 并且隨著振動態數目的變大形成的勢阱也會變深， 相應的勢阱支持的束縛態和準束縛態的壽命會變長并且不同電子態之間的波函數耦合也會變得強烈. 這也可以解釋為什么1.0 eV時基態的共振峰的數目多于其他能量.

圖 5 置換反應總的積分截面和振動分辨的積分截面Fig. 5. The total and vibrational state-resolved integral cross section of exchange reaction.

圖5 給出置換反應的總積分截面和振動分辨的積分截面. 它們的形狀與圖2中的反應概率類似，都是隨著碰撞的增加單調遞增. 并且隨著碰撞的增加， 其他振動激發態的通道逐漸打開. 產物的振動態分布也是隨著振動激發態的增加逐漸遞減. 主要的振動態分布集中在基態和第一激發態上.

圖6給出了置換反應在碰撞為0.8， 1.2，1.6和2.0 eV時的產物分布. 與圖4類似， 隨著碰撞能的升高， 振動態的數目和轉動量子數的數目都增加， 表明更多的碰撞能轉化為內能.在0.8和2.0 eV時的基態出現了有趣的雙峰結構.1.2和1.6 eV基態的峰偏向于較大轉動量子數的位置.

3.3 微分截面

圖7給出了不同碰撞能下抽取反應和置換反應的微分截面. 對于抽取反應， 在低碰撞能時主要有后向和側向散射信號， 這表明在低碰撞能時， 頭碰頭的反彈機制反應機制占據主導地位. 隨著能量的升高， 后向散射變的不明顯， 前向散射變得越加明顯， 這表明反應機制由頭碰頭的反彈機制轉變為剝離反應機制. 側向的信號在Li等[25]的分析中是因為勢能面上兩個電子態交叉的勢阱引起的， 是不可靠的. 對于置換反應， 在低碰撞能時， 散射信號主要集中在后向散射. 隨著碰撞的增加， 后向散射信號變得明顯， 同時側向和前向的散射信號也變得明顯. 不難看出對于置換反應， 反彈反應機制一直占據主導地位. 隨著碰撞能的增加， D的速率變得越來越大， 使其帶走質量相對較重的Br原子成為可能， 因此出現了側向和前向的散射信號.

3.4 速率常數

抽取反應和置換反應在不同溫度范圍內的速率常數分別示于圖8(a)和圖8(b)中. 為了與相應的理論和實驗結果比較， 文獻[1，6，24]的結果也列入到了圖8(a)中. 對于抽取反應， 速率常數隨著溫度的升高線性增加. 此外， 本文結果與Zhang等[24]的非絕熱結果以及實驗值都十分吻合. 盡管在低溫時出現了一些微小的差距. 這可能是因為本文的結果是基于絕熱的勢能面， 另一方面與實驗結果比較需要包含轉動激發態的貢獻， 而本文只考慮了基態的結果. 圖8(b)給出了0—3000 K溫度范圍內置換反應的速率常數. 如圖8(b)所示， 速率常數隨著溫度升高而增加.

圖 6 在若干選擇的碰撞能下， 置換反應的產物的振轉分布Fig. 6. The ro-vibrational distribution of products for exchange reaction at several selected collision energies.

圖 7 (a) 在若干碰撞能下， 抽取反應的微分截面; (b) 在若干碰撞能下， 置換反應的微分截面Fig. 7. (a) The differential cross sections of abstraction reaction at several selected collision energies; (b) the differential cross sections of exchange reaction at several selected collision energies.

圖 8 (a) 在200-1000 K溫度范圍內， 抽取反應的速率常數以及文獻[1，6，24]的結果; (b) 在0-3000 K溫度范圍內， 置換反應的速率常數Fig. 8. (a) The rate constant of abstraction reaction and the values obtained from Refs.[1，6，24] in the temperature range from 200 to 1000 K; (b) the rate constant of the exchange reaction in the temperature range from 0 to 3000 K.

4 結 論

基于Li等的勢能面采用含時量子波包方法和二階分裂算符傳播子對D + DBr反應的抽取通道和置換通道進行了動力學計算. 在量子態分辨的理論層次上報道了反應概率、積分截面、微分截面、產物振轉態分布以及速率常數等動力學信息. 積分截面結果與Zhang等[24]結果十分吻合， 盡管在高碰撞能部分有一些微小的差距. 速率常數以及實驗結果與Zhang等[24]的結果進行了比較. 結果表明，本文結果與實驗結果十分吻合. 微分截面信息表明， 對于抽取反應在低碰撞能時， 反彈機制占據主導地位. 剝離反應機制在高碰撞能時占據主導地位. 對于置換反應， 反彈機制一直占據主導地位，然而隨著碰撞能升高時， 逐漸出現前向和側向的散射信號.