康威的生命游戲

當代最偉大的數學家之一英國數學家約翰·霍頓·康威（John Horton Conway）因新冠肺炎逝世，享年82歲。他在群論、數論、代數、幾何拓撲、理論物理、組合博弈論和幾何等領域，做出了重大貢獻。（如圖1）

約翰·霍頓·康威（1937—2020）

這位天才數學家在劍橋研究數學同時還熱愛著游戲，他把大把時間用在了玩游戲，發明小游戲，或者改寫那些他認為無聊的游戲的規則上。

回看康威一生對數學做出的數不清的貢獻中，游戲在其中占據了很大的比重。其中最著名的一個游戲，就是在1970年發明的生命游戲（Conways Game of Life）。（如圖2）

生命游戲

這是一種可以模擬自然界的生命演化的游戲，它是第一個元胞自動機。在這個二維世界中，每個方格可以居住一個“生”和“死”狀態的細胞，用黑和白來表示。細胞的生死存續受到周圍8格的影響。

1.繁殖：如果一個細胞周圍有3個細胞為生，則該細胞為生（即該細胞若原先為死，則轉為生，若原先為生，則保持不變） 。

2. 穩定：如果一個細胞周圍有2個細胞為生，則該細胞的生死狀態保持不變。

3. 擁擠：在周圍細胞高于3個的情況下，則該細胞因擁擠而死（即該細胞若原先為生，則轉為死，若原先為死，則保持不變）。

4. 孤獨：在周圍細胞低于2個的情況下，則該細胞因孤獨而死（即該細胞若原先為生，則轉為死，若原先為死，則保持不變）。

生命游戲的規則基于相鄰細胞的ON或OFF數目。為了簡化這些規則的應用，可以只計算出處于 ON 狀態的相鄰細胞總數。這幾條規則用Python代碼表示如圖。（如圖3）

if 周圍細胞小于2或 周圍細胞大于3 則 該細胞 OFF

else if 周圍細胞等于3則 該細胞 ON

設定圖像中每個像素的初始狀態后依據上述的游戲規則演繹生命的變化，由于初始狀態和迭代次數不同，將會得到令人嘆服的優美圖案。（如圖4、5、6）

滑翔者：它會向右下角前進

輕量級飛船：它向右邊飛翔

1974年康威在玩生命游戲

這個游戲帶來的最大啟示，或許就是它展示了，生命游戲中的細胞只需要遵循幾條簡單規則，就可以演化出高度復雜的特征，當格子足夠多時甚至可以演化出類似理性思維的活動。

1974年康微在玩生命游戲

由于這個游戲核心算法簡潔，展示效果神奇，且具有生物學、社會學甚至哲學上的意義，因此成為了學習編程語言的經典習題。網上有大量的學習資料，不計其數的程序員制作了從簡陋到完美的源程序，由于資料齊全非常適合已經有一定編程基礎的人實操提高。

除了學習用不同語言編寫生命游戲之外，找到可以長期穩定生存的初始圖案或神奇的循環的復雜圖案也是生命游戲的核心玩法。

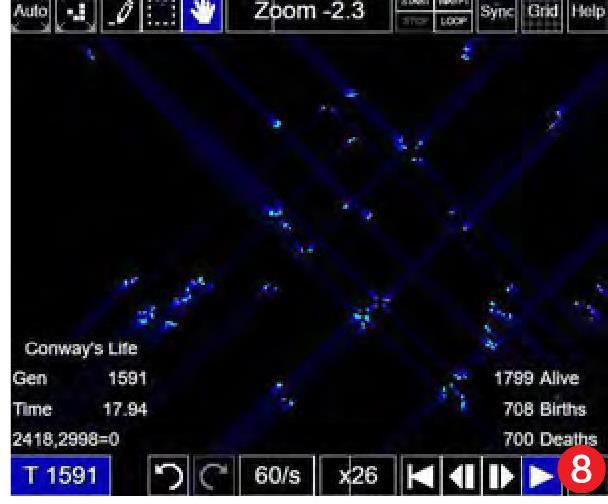
conwaylife上分享的圖案

在www.conwaylife.com、生命游戲吧、Golly吧里聚集著一批愛好者，他們會分享自己找到的神奇圖案。

Golly是一款專門模擬各類型元胞自動機（康威規則是最初的一種元胞自動機）的免費軟件。（下載地址：sourceforge.net/projects/golly/）

Golly中內置豐富的規則和圖案

除了可以自己繪制初始圖案外，Golly中內置了豐富的規則和圖案，選擇運行能看到各種神奇的效果。與網友交流分享成果也非常方便，把類似x = 80， y = 78， rule = B3/S23……的長串代碼直接復制粘貼在舞臺上就可以了。

脈沖星：一顆周期爆發的星星