Scrratch計算質數
在數學王國中,數學家根據不同數的特性給它們起了不同的名字,有的叫奇數,有的叫偶數,還有的叫質數……今天我們就來探討一下這個質數。
質數又稱素數,一個大于1的自然數,除了1和它自身外不能被其他自然數整除的數叫做質數,否則稱為合數。質數的個數是無窮多的,2、3、5、7、11這些都是質數。懂得什么是質數后,我們就會考慮如何做一個程序判斷該數是不是質數呢?雖然質數是無窮多個,我們能不能計算出100以內的所有質數呢?
已知,質數就是只能被1和它自身兩個數相除的數。因此,要判斷一個大于2的自然數n是不是質數(默認2是為質數),最簡單的辦法就是看n能不能被2到n-1中的某個數整除。只要有一個數能被n整除,n就是合數;如果都不能整除,n就是質數。比如97,我們就看它能不能被2到96中的某一個數整除。很顯然97不能被2到96中的數字給整除,所以97是一個質數。
這個方法雖然簡單粗暴,卻也有很大弱點,就是隨著數字變大會消耗很長的運算時間。如果數字非常巨大還用手工計算當然是不可能,而使用計算機來計算卻還是有那么一點希望的,計算質數也是測試計算機運算能力的一個常用辦法呢。
好了現在我們先來看看判斷某一個數字是不是質數的流程圖。
判斷輸入的數字是否能被i給整除,如果該數字能被i整除了(余數=0),那么該數就不是質數,是合數,如果不能,則該數字就是質數。
在此基礎上我們從2開始依次判斷每個數是不是質數,如果是的話就加入到質數列表里,否則加入合數列表。還有幾個技巧就是當出現整除情況后,怎樣停止本次循環,我們使用直接賦值n=1完成循環判斷。然后去判斷下一個自然數是不是質數。

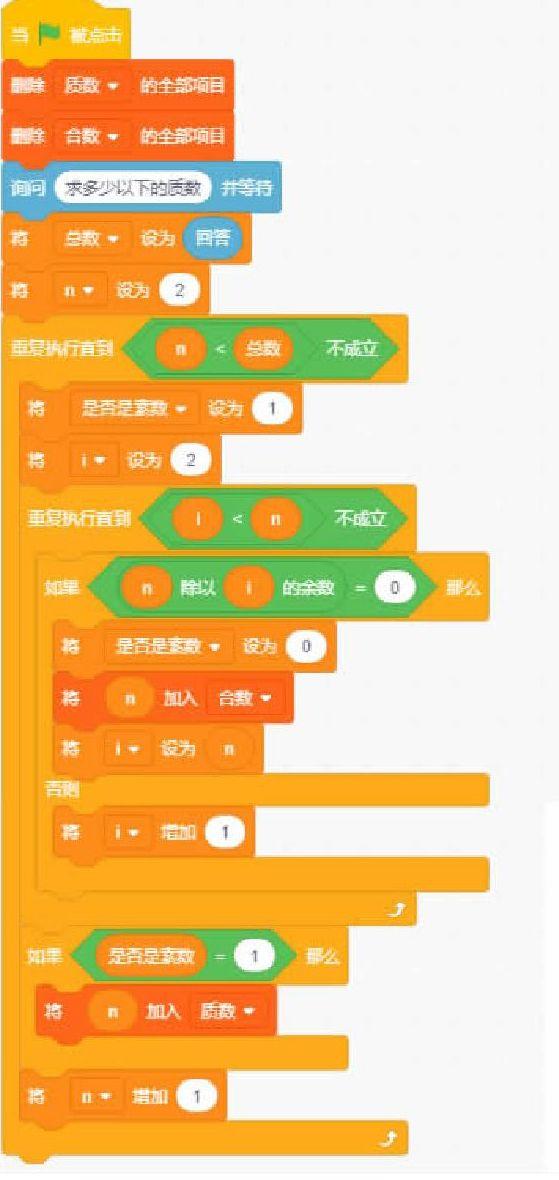
結合流程圖和程序代碼,我們一起來讀懂代碼。
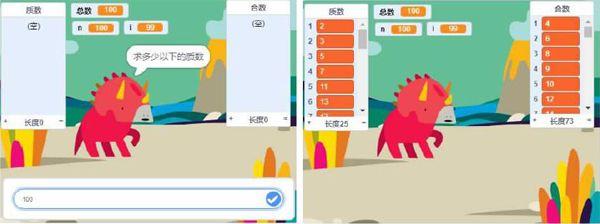
總數是用戶設定的計算范圍。
變量n是總數以內的自然數從2開始,依次遞增。
變量i作為除數,取值范圍2到n。
變量“是否為質數”用于記錄判斷n是否質數的結果。初始默認這個數是素數標記為1,如果能被整除那么就改變值為0,即不是質數,停止本次重復執行。
梅森素數
提前停止本次重復是一個減少計算量的小技巧。因為需要重復執行到i=n,一旦遇到可以整除時就直接修改i的值,使執行結束的條件成立,減少不必要的運算量。
每個自然數n重復執行除法判斷結束后根據變量“是否為質數”來確定最終結果,如果等于1就是質數,添加進質數列表,否則加入合數列表。
小知識:梅森素數
與質數(素數)有關的“互聯網梅森素數大搜索(GIMPS)”項目是旨在找到更大的梅森素數——既是梅森數(少量素數可寫成“2的n次方減1”<2^n-1>的形式)又是素數(質數)的數。
手工運算發現的最大梅森素數是1876年數學家盧卡斯發現的2^127-1.這是一個39位的數。2018年,計算機發現了第51個梅森素數:2^82589933-1(被稱為M82589933),共有24862048位。

