泄洪閘導墻穩定與應力對孔口寬度敏感性分析

彭兆軒，吳 濤，李 江

(新疆水利水電規劃設計管理局，新疆 烏魯木齊 830000)

沖砂泄洪閘是水利工程中運用較為廣泛的泄水建筑物，尤其是在水庫泄水工程中運用極為普遍，而沖砂泄洪閘兩側的導墻結構又是保證水庫安全泄洪的關鍵受力結構。因此，對導墻結構的研究顯得極為重要。劉曉平[1]等人以某低水頭電站為實例，采用物理模型與數值分析相結合的方法分析了導墻的布置形式對進水口流態的影響。邵凱、冉堯、張生財等人[2- 4]通過對導墻結構形式的不斷優化，提高了效能效率，降低了水流對周邊結構的沖刷，實現了水流平穩順暢的進入下游河道。程帥、杜占科等人[5- 6]將簡單面上的抗滑穩定有限元分析方法加以改進，推廣到復雜地基面上，結合有限元軟件進行了溢洪道導墻抗滑穩定分析。黃耀華、李振龍等人[7- 8]應用大型通用有限元軟件對溢洪道導墻壩段進行了應力計算，得到了溢洪道導墻壩段及主要部位的大、小主應力。練繼建等人[9]以某大型水電站導墻為研究對象，建立了結構損傷評估流程體系，簡要分析了導墻的裂縫成因。魏麗琴等人[10]將物理模型試驗與數值模擬計算相結合，得到導流明渠進口導墻體型方案。陳玲玲等人[11]以三峽溢流壩左導墻為研究對象，在總結了水彈性模型流激振動試驗和相應計算的基礎上，對導墻模型結構和原型結構做了流激振動響應分析比較，最后對導墻安全度進行了綜合評價。涂小兵等人[12]經研究發現，通過對明渠導墻采取工程措施可以滿足30年或50年一遇的超標準洪水，而對100年一遇的超標準洪水應采用基坑預充水過流的防洪方案。

通過上述眾多研究不難發現，大部分研究僅僅針對導墻結構本身，并沒有考慮相鄰結構或外部因素對導墻結構穩定及應力的影響研究。本文利用大型通用有限元軟件ABAQUS，針對某重力壩泄洪閘左導墻壩段進行三維實體建模，并分析了導墻壩段抗滑穩定及應力特性對孔口寬度的敏感性。

1 計算原理

水利工程中分析導墻壩段抗滑穩定主要方法與重力壩的抗滑穩定計算方法相似，大都采用剛體極限平衡法、有限元法和地質模型試驗法，在水工計算中常采用前兩種計算方法[13- 20]。依據SL319—2018《混凝土重力壩設計規范》[21]，在基本荷載組合和特殊荷載組合下運用剛體極限平衡法進行抗滑穩定計算。對于左導墻壩段按抗剪和抗剪斷強度公式分別計算。

K′=(f′∑W+C′A)/∑P

(1)

式中，K′—按抗剪斷強度計算的抗滑穩定安全系數；f′—抗剪斷摩擦系數；∑W—作用于壩體上全部荷載對滑動面的法向分值，kN；C′—抗剪斷凝聚力，kPa；A—壩基接觸面面積，m2；∑P—作用于壩體上全部荷載對滑動平面的切向分值，kN。

K=f∑W/∑P

(2)

式中，K—按抗剪強度計算的抗滑穩定安全系數；f—抗剪摩擦系數。

2 計算方法

根據上述計算原理，通過大型通用有限元軟件ABAQUS對某重力壩泄洪閘左導墻壩段進行三維有限元分析。首先按照面積相等原則，采用矩形斷面模擬防滲帷幕所在的地基橫斷面。同時，對排水孔幕所在的地基橫斷面，采用基于滲流量和水頭等價原則的“以縫代井列”方法進行等效模擬。計算并提取出各典型斷面處的揚壓力，代入抗剪和抗剪斷公式中進行左導墻壩段的側向穩定計算。

采用降溫法模擬錨索預應力的施加過程。降溫法指的是在材料定義中定義材料的溫度膨脹系數，然后定義溫度降低數值，達到給預應力錨索施加預應力的目的。通過降溫法計算錨索應力的公式[22]：

σ=α·E·ΔT

(3)

3 工程實例分析

3.1 工程概況

某水庫攔河擋水建筑物為重力壩，壩頂高程247.00m，最大壩高58.00m，正常蓄水位241.00m，總庫容3.25億m3。樞紐布置從右至左分別為右岸非溢流壩段、右7孔沖砂泄洪閘壩段、右導墻壩段、左5孔沖砂泄洪閘壩段、左導墻壩段、主機間壩段、安裝間壩段等，共19個壩段。樞紐區巖性為石英絹云母千枚巖夾含炭質絹云母千枚巖、炭質絹云母石英千枚巖，裂隙較為發育，鉆孔RQD平均值小于25%，巖體完整性較差。河床覆蓋層為沖積砂卵礫石，厚3.25～9.57m，基巖深槽部位厚14.22～18.17m。

左導墻壩段范圍為：壩左0+094.50m～壩左0+124.50m，壩上0+013.00m～壩下0+063.50m。左導墻墻頂高程為247.00m，最大高度為47.00m。左導墻既是泄洪閘的左邊墩，又是廠房的右邊墻。左導墻壩段在壩下0+017.00處設置有結構縫。左五孔設計最大單寬流量達161m2/s，堰面最大流速約為20m/s，屬于典型的低水頭，大單寬泄量閘壩式水利樞紐。左導墻壩段建基面高程200.00～205.00m，建基面巖體為弱風化及微風化千枚巖。

3.2 計算模型及邊界條件

根據泄洪閘左導墻壩段布置及其結構特征，運用美國SIMULIA公司開發的大型有限元軟件ABAQUS進行三維建模計算。左導墻壩段無強風化巖層，弱風化帶厚0～2.33m，弱風化底板高程一般在200m，建基面以下約20m處有一條由右岸傾向左岸的斷裂帶。根據一般工程經驗及本工程實際地質條件，計算模型基礎的選取范圍考慮為結構尺寸的1～2倍。有限元模型取導墻完整壩段，地基深度為87m，深入斷裂帶以下約67m；左側地基為56.00m、溢流堰右側地基為66.00m；導墻上、下游側的地基長度為88.50m，選取范圍約為導墻結構尺寸的1.5倍。預應力錨索采用桿單元模擬，利用降溫法進行預應力的施加，計算模型基本采用六面體實體單元，由于導墻內部灌漿排水廊道錯綜復雜以及壩基巖體內斷裂帶的存在，因此廊道及斷裂帶周圍采用了部分的四面體單元過度，左導墻模型共62116個節點，40966個單元。本次計算選用笛卡爾直角坐標系，X軸方向為壩軸向，從右岸指向左岸為正向；Y軸方向為順河向，從下游指向上游為正向；Z軸方向為豎向，沿壩高方向從下向上為正向。泄洪閘左導墻壩段三維有限元模型如圖1所示。

地基上游側和下游側分別施加y向約束，左側和右側分別施加x向約束，底部施加全約束，即固定支座。導墻壩段和壩基的接觸面通過設置Goodman接觸面單元考慮其不連續變形特性。接觸面模型參數參照類似工程經驗選取，見表1。

表1 Goodman接觸面模型參數

3.3 基本假定及材料基本參數

本次對該重力壩泄洪閘左導墻壩段三維有限元計算做如下基本假定：

(1)材料的密度、彈性模量、泊松比以及滲透系數等參數假定為各向同性。

通常情況下，祈使語氣的都是具有較高社會地位的人對于其下級或下屬使用。在政治類演講語篇中，演說者的地位都較于聽眾較高，因此，他們在自己的演說中使用祈使語氣代替陳述語氣能更好地凸顯他們所要表達的觀點，體現自己的權威性。

(2)壩體混凝土和微風化巖體按線彈性模型考慮，壩基接觸面按彈塑性模型考慮。

(3)考慮到左導墻壩段與相鄰壩段間均設置伸縮縫，不計相鄰壩段的影響。

本文對泄洪閘左導墻壩段三維有限元模型進行滲流分析、抗滑穩定分析以及應力變形分析，計算所需的材料參數為泄洪閘左導墻壩段混凝土、基巖、灌漿帷幕以及排水孔幕的滲透系數，見表2。

表2 左導墻壩段混凝土及其他結構材料的滲透系數

泄洪閘左導墻壩段各分區混凝土、預應力錨索以及壩基巖體的物理力學參數見表3。

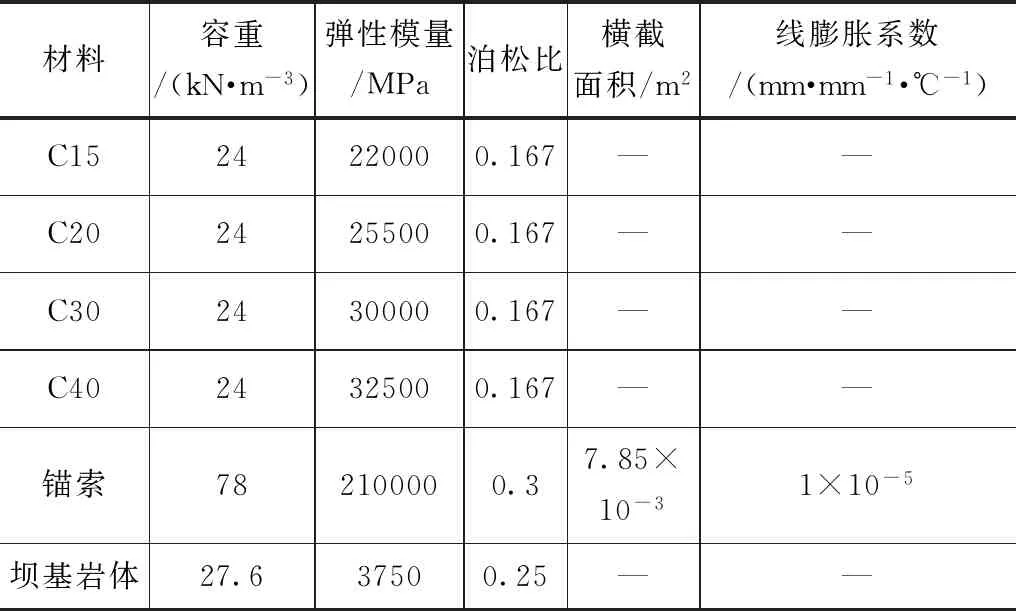
表3 左導墻壩段各分區混凝土、預應力錨索及壩基巖體的材料參數

3.4 計算方案

本次計算結合校核洪水位工況，針對左導墻壩段壩下0+015.25及壩下0+056.00兩個典型橫斷面，在保持溢流堰堰體長度和高度均為原設計值的前提下，擬定了左導墻壩段右側泄洪閘孔口寬度B分別為3.0、4.5、6.0、7.5m共四種方案。基于上述四種寬度方案的滲流計算，確定兩個典型橫斷面在建基面處的揚壓力分布，考慮結構自重、靜水壓力、動水壓力和揚壓力等荷載作用，結合上述兩個典型橫斷面進行左導墻壩段側向抗滑穩定及應力關于泄洪閘孔口寬度的敏感性分析。左導墻典型縱、橫斷面示意圖如圖2—3所示。其中，左導墻壩段的典型縱斷面包括壩左0+099.00(左導墻壩段與沖砂泄洪閘閘堰銜接處)、壩左0+096.75(溢流堰壩段中心線)、壩左0+103.50(縱向灌漿排水廊道中心線)和壩左0+112.00(左導墻壩段中間部位)共4個縱斷面；左導墻壩段的典型橫斷面包括壩下0+015.25(交通排水廊道中心線)和壩下0+056.00(溢流堰臺階中間部位)共2個橫斷面。

圖2 左導墻各典型橫斷面示意圖

4 有限元計算結果分析

4.1 典型橫斷面揚壓力水頭關于孔口寬度B的敏感性分析

通過對泄洪閘左導墻壩段的三維有限元滲流計算分析，可得出在不同孔口寬度B時，壩下0+015.25和壩下0+056.00兩個典型橫斷面在建基面處的揚壓力水頭分布規律，如圖4—5所示。

由圖4—5可以看出，兩個典型橫斷面在建基面處的揚壓力水頭分布規律基本一致，孔口寬度B越大，揚壓力水頭下降越緩慢，但揚壓力水頭下降幅度對孔口寬度的敏感性較弱，總體呈現出先驟降再逐步緩慢上升的分布特征。從溢流堰中心至溢流堰與導墻壩段連接處的揚壓力水頭落差較大，降低幅度大概為83%左右；在壩左0+103.50處，揚壓力水頭降至最低值；隨后雖有增加但增幅較小。這是因為在壩左0+103.50處設置了灌漿排水廊道和排水孔幕，所以在此處揚壓力水頭最小，這也更加說明了有限元計算的準確性與合理性。

4.2 典型橫斷面側向抗滑穩定關于孔口寬度的敏感性分析

根據不同孔口寬度方案，結合壩下0+015.25及壩下0+056.00兩個典型橫斷面的三維有限元滲流計算所獲得的壩基揚壓力結果，對上述兩個典型橫斷面分別按抗剪斷和抗剪強度進行了側向抗滑穩定計算，計算結果見表4。根據規范要求，對于特殊組合的校核洪水位工況按抗剪斷強度公式計算的抗滑穩定安全系數K′不應小于2.5，按抗剪強度公式計算的抗滑穩定安全系數K不應小于1.0。

圖3 左導墻各典型縱、橫斷面示意圖

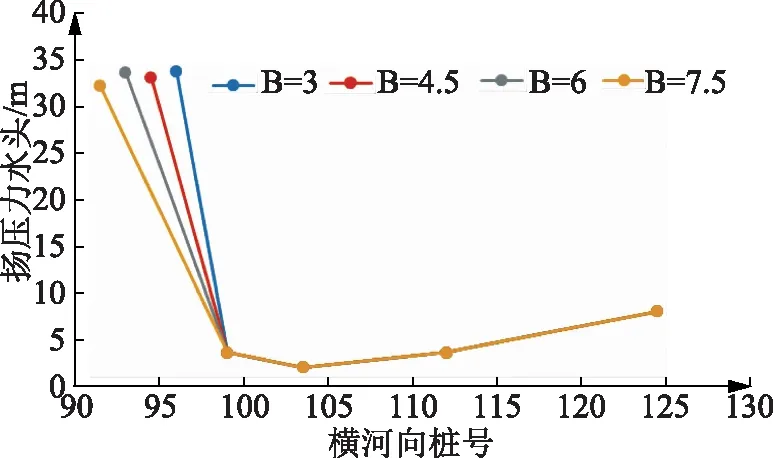
圖4 壩下0+015.25在建基面處揚壓力水頭分布

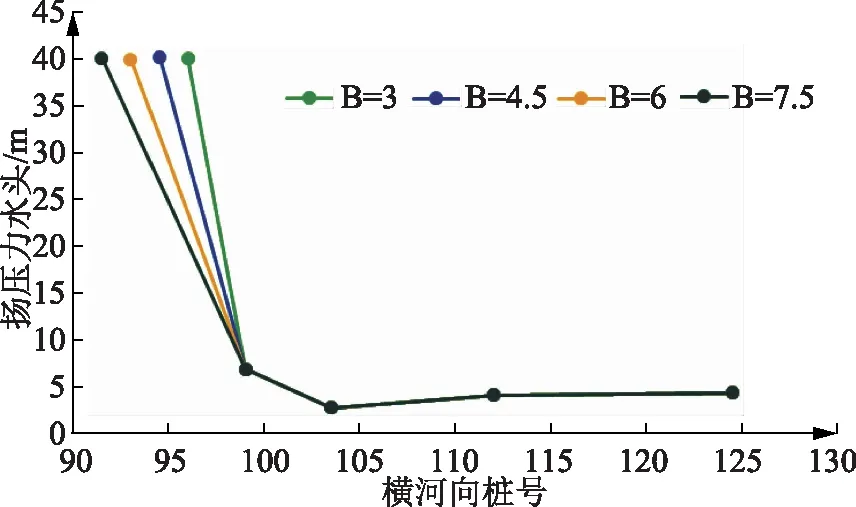
圖5 壩下0+056.00在建基面處揚壓力水頭分布

從表4可以看出，在不同孔口寬度的方案下，兩個典型橫斷面按抗剪強度公式和抗剪斷強度公式計算的抗滑穩定安全系數隨著孔口寬度的增加而增大，且均滿足泄洪閘左導墻壩段側向抗滑穩定要求。從表4中只能反映出抗滑穩定安全系數隨著孔

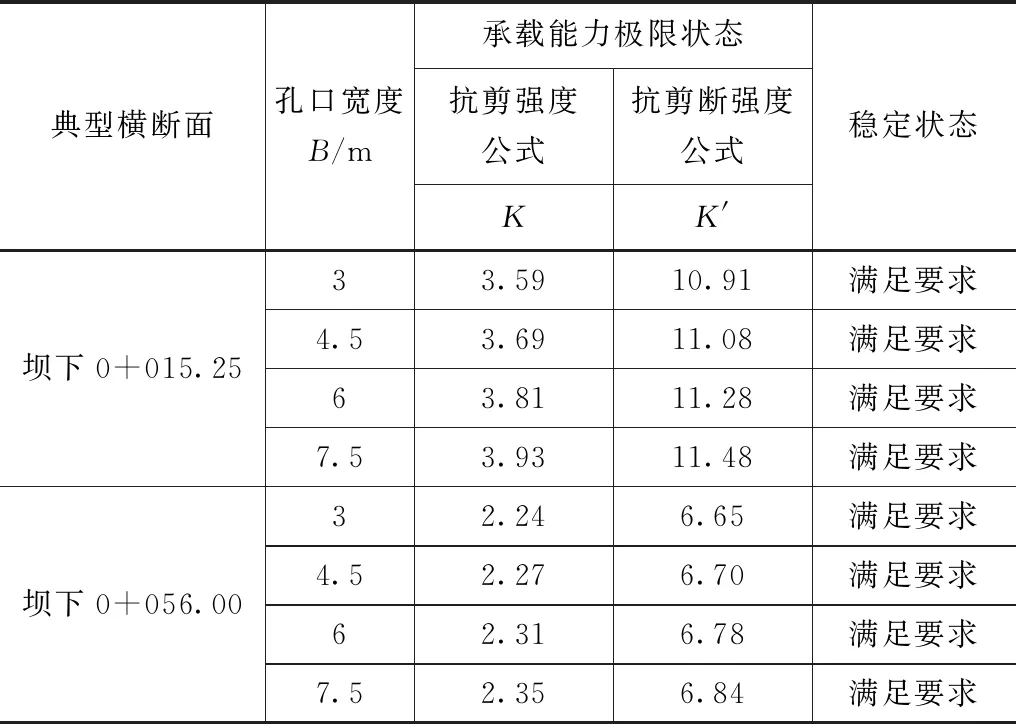
表4 典型橫斷面在不同孔口寬度B下的側向抗滑穩定計算結果

口寬度的增加而增加，無法判斷其對孔口寬度的敏感性強弱。為此，將不同孔口寬度計算得到的抗滑穩定安全系數相較上一級增加的幅度大小作為其敏感性強弱的判斷標準，如圖6所示。

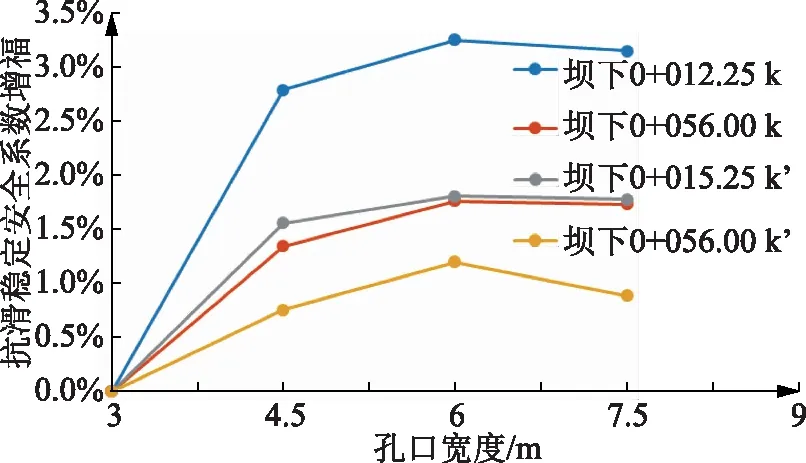
圖6 各典型橫斷面抗滑穩定安全系數增幅

從圖6中可以看出，隨著孔口寬度的增加，兩個典型橫斷面的抗滑穩定安全系數雖都有所增加，但其增長幅度卻不同。壩下0+056.00處的抗滑穩定安全系數K′隨著孔口寬度的增加，其增長幅度上下波動較大，所以該典型橫斷面的側向抗滑穩定對孔口寬度較為敏感。其余橫斷面上的抗滑穩定安全系數增幅雖略有波動，但上下波動較小，其對孔口寬度的敏感性較弱。

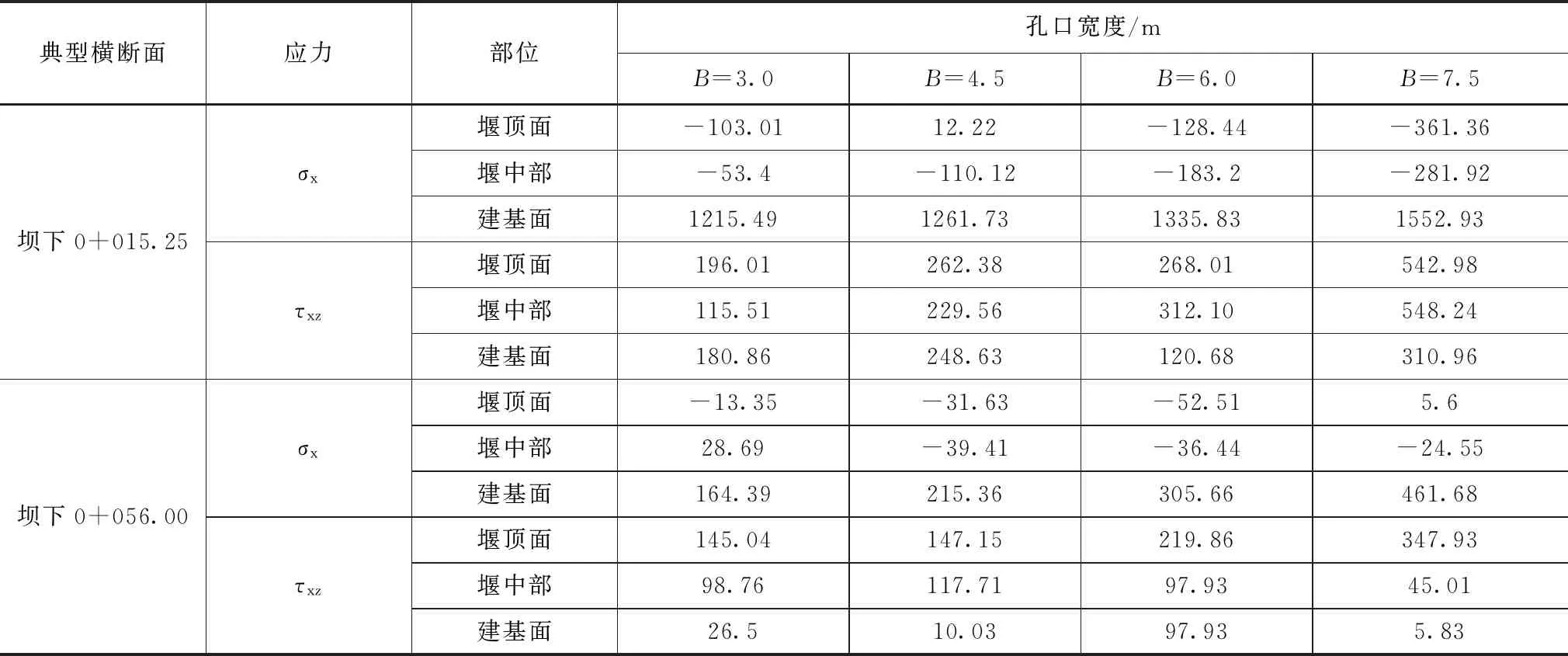
表5 兩個典型橫斷面在不同孔口寬度下的應力計算結果表 單位：kPa

4.3 典型橫斷面應力關于孔口寬度B的敏感性分析

針對上述壩下0+015.25和壩下0+056.00兩個典型橫斷面，對不同孔口寬度方案分別在相應的三維有限元模型下進行應力變形計算。應力計算結果的符號約定如下：各向正應力以受拉為正，受壓為負；各向剪應力以其作用方向沿坐標軸正向為正，以其作用方向沿坐標軸反向為負。兩個典型橫斷面在不同孔口寬度下壩左0+099.00(左導墻壩段與沖砂泄洪閘閘堰銜接處)處的應力計算結果見表5，兩個典型橫斷面在壩左0+099.00處的壩軸向正應力σx及豎向剪應力τxz(τxz取絕對值)在不同孔口寬度上的分布情況如圖7—8所示。

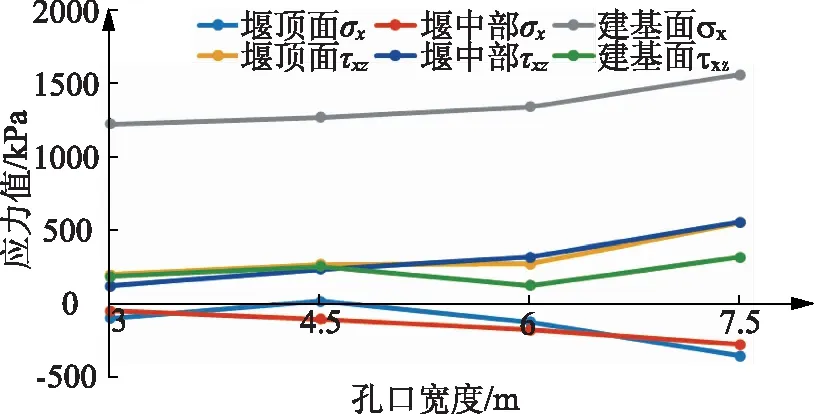
圖7 壩下0+015.25橫斷面在壩左0+099.00處的壩軸向正應力σx及豎向剪應力τxz與孔口寬度關系圖

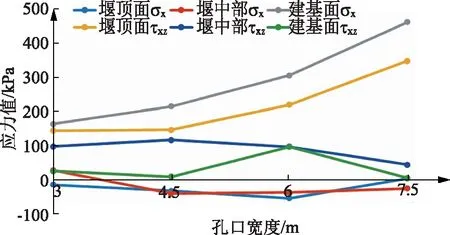
圖8 壩下0+056.00橫斷面在壩左0+099.00處的壩軸向正應力σx及豎向剪應力τxz與孔口寬度關系圖

從圖7—8應力分布規律中可以看出，在上述四種孔口寬度方案下，典型橫斷面壩下0+015.25和壩下0+056.00在壩左0+099.00處沿壩軸向正應力的分布規律基本一致，且兩個橫斷面沿壩軸向正應力最大值均出現在高程為200.00m的建基面處。壩下0+056.00在建基面處的正應力σx隨著孔口寬度的增加，其增長幅度遠大于壩下0+015.25在建基面處的正應力增長幅度。由此可以看出，壩下0+056.00在建基面處的正應力對孔口寬度更為敏感。兩個典型橫斷面在堰頂面的剪應力τxz隨著孔口寬度的增加均呈現出上升的趨勢，且壩下0+056.00的剪應力增長幅度較大，其對孔口寬度更加敏感。堰中部和建基面處的剪應力變化幅度較小，且壩下0+015.25在堰中部和建基面處的剪應力總體呈現緩慢增大的趨勢，而壩下0+056.00則呈現出緩慢減小的趨勢，其對孔口寬度的敏感性較弱。

根據表5可知，壩下0+015.25沿壩軸向的最大拉應力大小依次為1215.49、1261.73、1335.83和1552.93kPa。按應力控制標準，建基面沿壩軸向拉應力應小于1.10MPa。因此，四種孔口寬度方案在壩下0+015.25的壩軸向拉應力均不滿足強度要求，還需進一步進行結構優化設計。壩下0+056.00沿壩軸向的最大拉應力大小依次為164.39、215.36、305.66和461.68kPa，均滿足強度要求，不存在因拉應力過大而造成混凝土開裂的問題。兩個典型橫斷面壩下0+015.25和壩下0+056.00豎向最大剪應力均未超過1.0MPa，且普遍偏小。根據應力控制標準，其均滿足強度要求。

5 結論

本文通過對泄洪閘左導墻壩段的計算分析，得出以下結論：

(1)兩個典型橫斷面在建基面處的揚壓力水頭總體呈現出先驟降再逐步緩慢上升的分布特征，其對孔口寬度的敏感性較弱。

(2)隨著孔口寬度的增加，兩個典型橫斷面的抗滑穩定安全系數也隨之逐漸增大且均滿足側向抗滑穩定要求。壩下0+056.00處的抗滑穩定安全系數K′對孔口寬度較為敏感。

(3)兩個典型橫斷面沿壩軸向的σmax均出現在建基面處，τmax均出現在堰頂面，壩下0+056.00在建基面處的σ以及τ對孔口寬度更為敏感。導墻底部的最大拉應力超出應力控制標準，建議進行結構優化設計。