左刪失恒定應力部分加速壽命試驗下逆Rayleigh分布的參數估計

龍兵，張忠占

（1.荊楚理工學院數理學院，湖北荊門448000；2.北京工業(yè)大學應用數理學院，北京100124）

0 引 言

在可靠性壽命試驗中經常會遇到一些長壽命的產品，在正常使用條件下進行試驗，通常需要花費很長的時間。為了更快地獲得失效數據進行可靠性分析，可以選擇采用加速壽命試驗，即將產品置于更嚴酷的應力條件下試驗，這樣可以加速性能的退化，使產品更快地失效。將所有的受試產品都放在加速環(huán)境下試驗，稱為加速壽命試驗，若只放一部分產品，則稱部分加速壽命試驗。由恒定應力部分的加速壽命試驗數據可估算得到加速因子，從而實現(xiàn)兩種應力水平下壽命數據的轉換，節(jié)省試驗時間和經費，并能很快得到統(tǒng)計分析結果。部分加速壽命試驗已經引起了一些統(tǒng)計學者的重視，形成了很多研究成果。ISMAIL[1-2]基于截尾樣本，在恒定應力部分加速壽命試驗模型下，討論了Weibull分布的參數及加速因子的極大似然估計，確定了最優(yōu)試驗方案。ISMAIL等[3-4]在恒定應力部分加速壽命試驗模型下，求得了II型Pareto分布和逆Weibull分布的參數及加速因子的極大似然估計，通過最小化廣義漸近方差給出了兩種應力水平下樣本的最優(yōu)分配方案。文獻[5-6]也在恒定應力加速壽命試驗模型下，討論了Pareto分布和逆Weibull分布的可靠性問題。

逆Rayleigh分布作為可靠性領域的一個重要分支，其統(tǒng)計性質值得深入研究。針對該分布的研究成果已有很多，JEBELY等[7]在完全觀測樣本下討論了逆Rayleigh分布的密度函數和分布函數的估計。文獻[8-10]在完全觀測樣本下用貝葉斯方法研究了逆Rayleigh分布的統(tǒng)計推斷問題。在壽命測試試驗中，截尾是大多數壽命數據集不可避免的特征，NAVID等[11]討論了在單截尾和雙截尾數據下逆Rayleigh分布的貝葉斯分析。與已有文獻不同，本文將基于左刪失樣本，在部分加速壽命試驗模型下，分別用經典方法和貝葉斯方法討論逆Rayleigh分布的統(tǒng)計性質，并比較這兩種方法所得到的參數估計值。

1 基本假設和模型描述

在應力水平S0，S1(S0＜S1)下進行壽命試驗，其中S0為正常應力水平，S1為加速應力水平。基本假設如下：

A 1 在應力水平S0,S1下，受試產品有相同的失效機理。

A2 在應力水平S0下，產品的失效時間為t；在應力水平S1下，產品的失效時間為x，滿足t=βx，其中，β(β＞1)為加速因子，且t與x相互獨立。

A3 在應力水平S0下，產品的失效時間t服從逆Rayleigh分布，其分布函數和概率密度函數分別為

其中，θ＞0為尺度參數。

根據假設A 1～A 3，在應力水平S1下，產品的失效時間x服從逆Rayleigh分布，其分布函數和概率密度函數分別為

即在應力水平S1下，產品的失效時間x服從參數為λ的逆Rayleigh分布。

現(xiàn)有n個受試產品被隨機分成2組，它們的容量分別為n0,n1。其中n0個樣品被安排到正常應力水平S0下進行壽命試驗，n1個樣品被安排到加速應力水平S1下進行壽命試驗。在應力水平Si(i=0,1)下進行左刪失試驗：對ni(i=0,1)個產品在0時刻進行壽命試驗，直到時刻τi(i=0,1)時進行觀測，此時發(fā)現(xiàn)已經有di(i=0,1)個產品失效，但不知其失效時刻，此后進行跟蹤觀測，可得到剩余的mi=ni-di(i=0,1)個產品的失效時刻。設觀測到的失效時刻分別為t=(t1,t2,…,tm0)（在應力水平S0下）和x=(x1,x2,…,xm1)（在應力水平S1下）。

2 極大似然估計

由上述試驗數據，在應力水平S0下的似然函數為

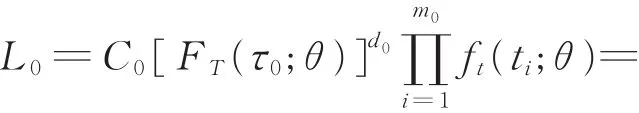
其中，C0＞ 0，且與θ無關。

在應力水平S1下的似然函數為

其中，C1＞0，且與λ無關。

由于在不同應力水平下進行的壽命試驗是相互獨立的，因此在左刪失恒定應力部分加速壽命試驗下的全似然函數為

用對數似然函數ln L求關于θ,λ的偏導數，得到似然方程組：

解得參數θ,λ的極大似然估計，分別為

由此，β的極大似然估計為

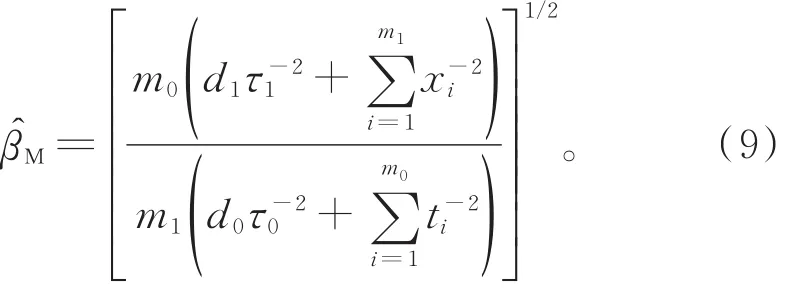
在式（9）中，令 d0=d1=0，m0=n0,m1=n1，不難得到在完全觀測樣本t=(t1,t2,…,tn0)和x=(x1,x2,…,xn1)下，參數 θ,λ,β的極大似然估計分別為

3 Fisher信息矩陣及近似置信區(qū)間

利用LOUIS[12]提出的缺失信息原則，計算觀測到的Fisher信息矩陣。缺失信息原則的概念可表述為觀測信息=完全信息-遺失信息。

記 η=(θ,β)，W 表示完全數據，X 表示觀測數據，IW(η)為完全信息矩陣，IX(η)為觀測信息矩陣，IW|X(η)為遺失信息矩陣，則觀測信息矩陣為

在完全數據情形下計算得到的完全信息矩陣為

在應力水平S0下，記Y=(Y1,Y2,…,Yd0)，則Y表示受試樣品在區(qū)間(0,τ0)內失效時刻構成的向量，由于無具體的值，因此視為遺失數據。同理，在應力水平S1下，記Z=(Z1,Z2,…,Zd1)，且Z表示受試樣品在區(qū)間(0,τ1)內失效時刻構成的向量。

根據條件密度公式，得到Yj(j=1,2,…,d0)的概率密度函數為

遺失信息矩陣為

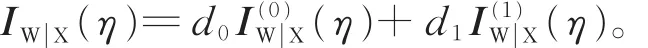
在應力水平 S0下，觀測區(qū)間 (0,τ0)的 Fisher信息矩陣為

在應力水平 S1下，觀測區(qū)間 (0,τ1)的 Fisher信息矩陣為

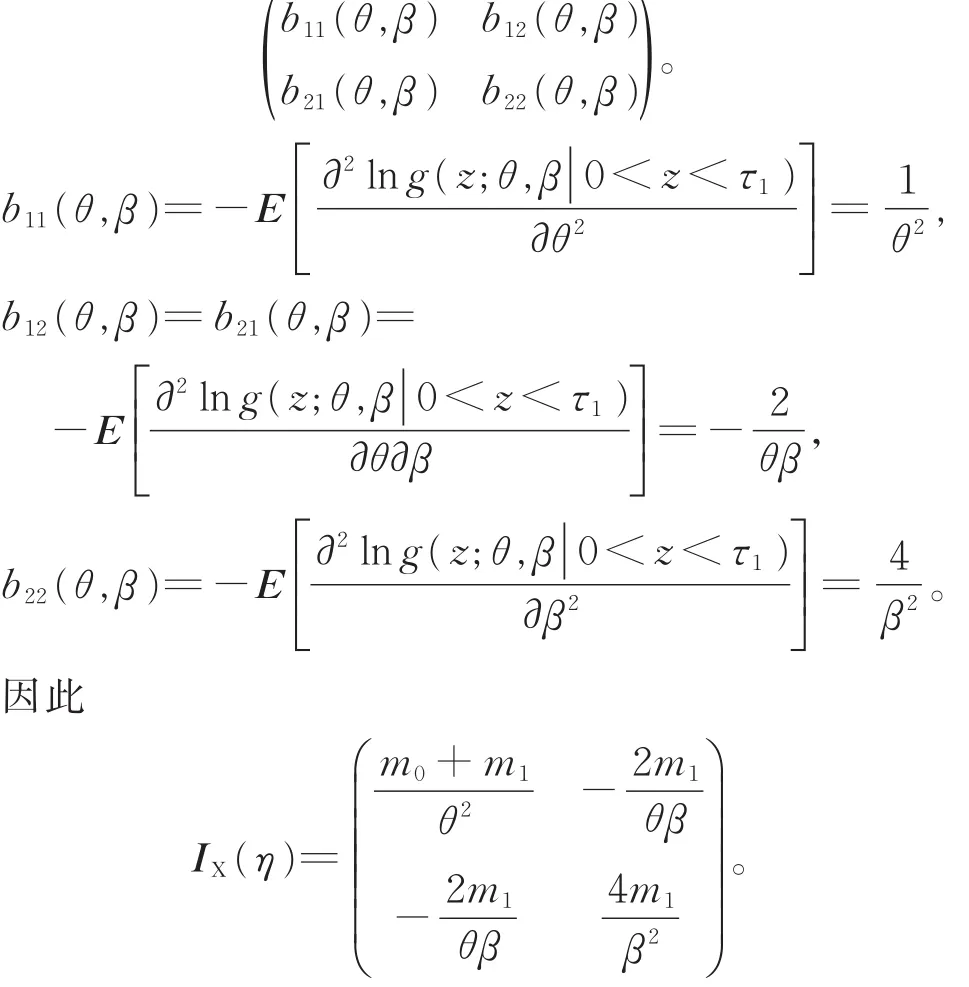
由文獻[13]知，當樣本量很大時，參數的極大似然估計 (θ?M,β?M)漸近服從二元正態(tài)分布，且期望為(θ,β)，方差、協(xié)方差矩陣為I-1X(η?)（觀測信息矩陣IX(η?)的逆矩陣），于是有

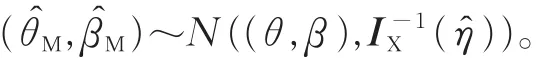
因此，參數θ,β的置信水平為100(1-γ)%的近似置信區(qū)間，分別為

其中，U11和U22為方差、協(xié)方差矩陣的主對角線元素，Zγ/2為標準正態(tài)分布的γ/2上分位數。

4 參數的貝葉斯估計

當有先驗信息可以利用時，采用貝葉斯方法通常可以提高估計的精度，因此，本節(jié)將計算參數θ和加速因子β的貝葉斯估計。

取參數θ的先驗密度為

其中a0＞0為超參數。由式（7）和式（11）及貝葉斯公式，可得θ的后驗密度為

在平方損失函數下，θ的貝葉斯估計為

由于在應力水平S0下，產品的可靠度函數為

因此，在平方損失函數下R0(t)的貝葉斯估計為

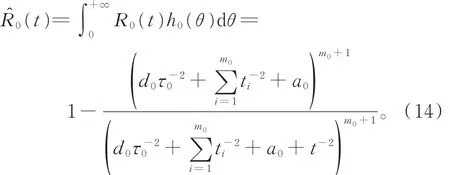
取參數λ的先驗密度為

其中a1＞0為超參數。由式（8）和式（15），可得λ的后驗密度：

由式（17）無法求出顯式解，可用數值積分求解。

下面用極大似然法估計超參數a0,a1。

在應力水平S0下，根據先驗分布π0(θ)，可得到經驗分布：

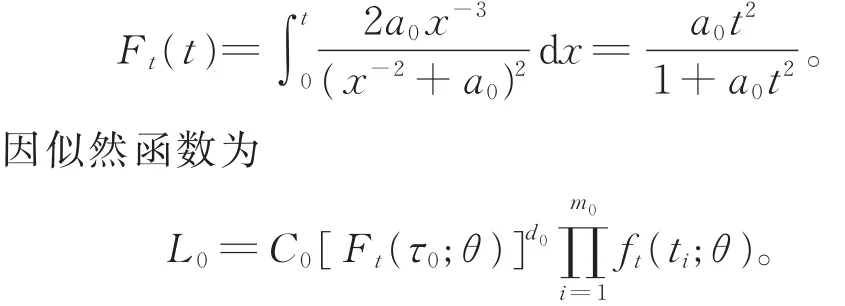
以 Ft(τ0),ft(ti)分 別 代 替 上 式 中 的Ft(τ0;θ),[ft(ti;θ )]，則有

記式（19）的最終迭代值為 a?0。

用類似的方法可求得超參數a1的估計值，記為a?1。將 a?0,a?1代入式（13）、（14）、（17），就可求得相應的貝葉斯估計值。

5 Monte Carlo模擬

對于不同的 n0,n1,θ,λ，從均方誤差（MSE）角度考慮分布參數和加速因子的估計性質。模擬過程如下：

第1步給定n0,n1及參數θ,λ的值。

第2步產生一個容量為n且服從均勻分布U(0,1)的獨立同分布樣本U1,U2,…,Un，令

ti=(-θ/ln Ui)1/2，i=1,2,…,n0，

xi=(-λ/ln Ui)1/2,i=n0+1,n0+2,…,n0+n1，則(t1,t2,…,tn0)(xn0+1,xn0+2,…,xn0+n1)就是分別來自于逆Rayleigh分布式（1）和式（5）的樣本。

第3步給定τ0,τ1的值，得到左刪失樣本。

第4步基于上面得到的左刪失樣本，分別計算θ,β的點估計。

第5步步驟2～步驟4重復1 000次，計算θ,β的均方誤差。

第 6步在不同的 n0,n1,θ,λ,τ0,τ1下，重復上述過程。

將以上步驟產生的隨機模擬結果列于表1，從表1中可以看到，隨著n0,n1的增加，參數θ,β的極大似然估計和貝葉斯估計的均方誤差逐漸減小，說明極大似然估計具有大樣本性質。在小樣本場合，貝葉斯估計要明顯優(yōu)于極大似然估計，隨著樣本量的增加，兩者的差距逐漸縮小。為了比較左刪失樣本下和完全觀測樣本下參數估計精度的差異，當θ=2，λ=1時，模擬計算了不同樣本容量下參數θ,β估計的均方誤差（見表2），結果顯示，完全觀測樣本下參數估計的精度要優(yōu)于左刪失樣本。

為了了解在具體樣本下各種估計的效果，取θ=3，λ=2，通過隨機模擬的方式分別產生容量為40和50的服從逆Rayleigh分布的樣本，在應力水平S0下（θ=3），按從小到大的順序排列：

0.914 ，1.017，1.102，1.109，1.148，1.194，1.277，1.309，1.341，1.381，1.416，1.502，1.515，1.673，1.674，1.687，1.713，1.834，1.875,1.922，2.125，2.211，2.245，2.427，2.617，2.859，2.918，3.022，3.062，3.489，3.567，3.571，3.601，3.725，3.787，3.935，4.965，5.098，5.633，6.288。

在應力水平S1下（λ=2），按從小到大的順序排列：0.784，0.793，0.887，0.938，1.056，1.093，1.098，1.108，1.109，1.144，1.184，1.192，1.235，1.253，1.255，1.261，1.263，1.382，1.389，1.401，1.410，1.427，1.451，1.485，1.505，1.513，1.515，1.538，1.546，1.608，1.643，1.673，1.767，1.787，1.884，1.949，2.014，2.192，2.368，2.552，2.792，3.012，3.042，3.065，4.501，4.841，5.121，5.758，6.142，8.505。

表1 左刪失樣本下參數估計的均方誤差Table 1 Mean square errors of parameter estimation under left censored samples

表2 完全觀測樣本下參數估計的均方誤差Table 2 Mean square errors of parameter estimation under complete observation samples

表3 參數的點估計及置信區(qū)間Table 3 Point estimation and confidence interval of the parameters

由τ0，τ1得到左刪失樣本，計算θ,β的極大似然估計、貝葉斯估計及置信水平為95%的置信區(qū)間，并分別記為θ?M，θ?B，(θ?L,θ?U)和β?M,β?B，(β?L,β?U)，相應的估計結果見表3。

由于參數真值θ=3,β=1.224 7，從表3的數據中可知，參數的貝葉斯估計比極大似然估計更接近參數真值，參數真值位于置信區(qū)間內。通常，隨著左刪失數據的增多，參數估計值與真值之間的差值以及置信區(qū)間的長度呈逐漸變大趨勢。

6 結 語

加速壽命試驗是利用產品壽命和應力水平之間的某種已知函數關系，估算產品在正常應力水平時的壽命。當產品壽命和應力水平之間的關系未知時，可采用恒定應力部分加速壽命試驗，此方法更適合新產品。用兩種應力水平下的試驗數據估計加速因子，然后將高應力水平下的壽命轉換為正常應力水平時的壽命。近年來，部分加速壽命試驗已被應用于可靠性統(tǒng)計推斷。在本文中，當產品的失效時間服從逆Rayleigh分布時，基于恒定應力部分加速壽命試驗數據，得到了分布參數和加速因子的極大似然估計及貝葉斯估計。由遺失信息原則計算極大似然估計的漸近方差，得到參數的近似置信區(qū)間。通過數值模擬說明樣本量對估計精度的影響，并將極大似然估計與貝葉斯估計做了比較，結果表明，在小樣本場合，貝葉斯估計要優(yōu)于極大似然估計。