空間對接鎖系精密鋼索張拉形變規律試驗研究

許春田，吳鑫楊，徐正東，王 朋

(1. 遼寧科技大學機械工程與自動化學院， 鞍山114051； 2. 上海宇航系統工程研究所，上海201109)

1 引言

航天器交互對接的關鍵對接機構[1]主要是由2 套鎖系組成的一個閉環傳動系統，每套鎖系中只有一把為主動鎖，通過鋼索經導向輪與其它被動鎖串聯(見圖1)。 鎖系對接是鋼索進行精密傳動的一種控制形式[2-3]，其同步性直接決定著兩航天器能否順利實現交會對接，是航天器交會對接的關鍵技術[4]。

受空間環境條件的制約，鎖系對接同步性主要通過裝配過程中對其串聯鋼索預緊載荷的調節來保證。 由于在這方面缺少必要的理論指導，主要憑經驗、反復操作來保證，不僅裝配效率低、成本高，而且保證困難。 針對這一問題，不少學者開展了大量研究并提出了一些改進措施，如譚益松[5]、潘東[6]等分別對空間大型末端執行器的鋼索捕獲動力學行為及特性進行了建模與仿真；李建廣等[7]建立了鎖系輪系傳動同步性模型；肖杰等[8]采用仿真方法對分析了鎖系運動同步性影響的主要因素，并提出了改進方向；張華等[9]通過鎖系驅動過程仿真，提出了改進索驅輪系運動同步性的建議；黃鐵球等[10]建立了單鎖數學模型，通過ADMAS 仿真分析了預緊力對鎖系同步性的影響；鄭云青等[11]建立了鎖系運動同步性與鋼索彈性變形間的關系模型，并提出了降低鋼索張力和形變量的控制方向。 然而，這些研究主要從鎖系對接運動學方面開展，并沒有涉及鋼索形變的影響。 鎖系串聯鋼索的連接結構及鋼索特性決定了其裝配是一個預緊載荷不斷施加與不斷調節的過程。 許春田等[12]雖從裝配方面對鎖系鋼索蠕變行為的影響進行了研究，但主要針對蠕變穩定階段，尚未論及非穩定階段鋼索形變的影響，并不完整。

為此，本文主要針對空間鎖系裝配預緊載荷施加過程中，因受鋼索蠕變、內部絲、股及繩輪間摩擦和轉角等因素引起張力松弛[13]而影響裝配精度及效率問題，對其鋼索形變規律開展試驗研究，以實現預緊載荷的有效控制與補償。

2 鋼索形變試驗

2.1 試驗原理

試驗系統組成如圖2 所示。 鋼索(3)在主、被動繩輪組件(5)、(1)間通過鎖緊螺母(6)進行固定，主、被動繩輪(12)、(13)半徑都為75 mm，其周緣刻度(8)分別用于記錄轉過的角度，被動繩輪(13)通過銷軸(11)實現固定。 減速器(9)通過聯軸器與主動繩輪組件(5)聯接，通過驅動主動繩輪(12)實現鋼索預緊載荷的施加，其大小則由兩導向輪(14)、(15)間鋼索(3)上裝有的張力儀(2)進行讀取。 每一位置測定時，因被動繩輪轉角θ2固定，根據鎖系實際裝配需求，預緊載荷對應的形變則用主動繩輪轉角θ1與其初始角的差值，即轉角偏差Δθ來表示。 由于鎖系裝配主要對其嚙合和鎖緊兩位置處的精度進行控制[7-9]，為此，試驗在其對應繩輪轉角分別為60°(嚙合)和180°(鎖緊)處展開。

圖2 試驗系統Fig.2 Experiment system

2.2 試驗樣本

鋼索在載荷作用下會發生彈性、粘彈性、粘塑性及塑性等復雜的變形[14]，在鎖系裝配過程中，如果不加以控制，將導致其串聯鋼索在預緊載荷作用下出現松弛而影響其對接同步性。 因不同結構及材質的鋼索在預緊載荷作用下所表現出的形變行為有所區別[15]，為具有針對性，本研究試驗樣本均為航天用類型為6x19 s＋IWS、1Cr18Ni9Ti鋼索， 其力學性能及結構參數分別見表1。

表1 鋼索力學性能及結構參數值Table 1 Mechanical performance and structure parameters of the cable

為降低測量誤差，以更精確地分析不同工況條件下鋼索形變行為，試驗以3 組鋼索為樣本，每組包括2 根，分別用于鎖系嚙合與鎖緊兩位置處鋼索形變行為的研究。 其中，樣本第1 組鋼索未經預張拉；第2、3 組分別為預先經過24 h 和48 h采用500 kg 配重進行靜力加載預張拉。 按照圖3顯示加載時程，并考慮鋼索松弛行為，分別以間隔5 min、2 h、5 h 和24 h 采用緩慢加載保壓方式進行預緊載荷的施加及試驗數據的測定。

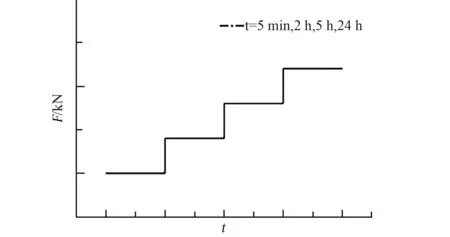
圖3 預緊載荷加載時程Fig.3 Preload time-history

2.3 張拉工藝

1)調節鋼索兩端鎖緊螺母，使主動繩輪(12)上鋼索固定端A 在其入口B 處對應轉角θ1為0°，張力儀(2)顯示的預緊載荷為0.2 kN 后， 將指針(7)指向繩輪上的某一刻度作為初始基準。

2)通過減速器(9)驅動主動繩輪(12)相對初始基準轉過60°，用銷軸(11)固定被動繩輪(13)，并將指針指定值作為60°位置數據測定的基準。

3)分別以間隔5 min，通過緩慢施加保壓方式施加預緊載荷直至3 kN，記錄每次張力儀顯示值及指針對應的刻度，則相應的鋼索形變就是該刻度值與60°基準值間的差值。

4)同步驟3，分別完成以間隔2 h、5 h 和24 h保壓延時加載方式下的鋼索形變數據的采集。

5)安裝第2 根鋼索，在步驟1 基礎上，驅動主動繩輪旋轉到180°，同步驟3 ～4，完成轉角180°處其形變數據的采集。

6)依據上述步驟1 ～5，分別完成3 組鋼索樣本數據的采集。

為降低因鋼索初始長度差異導致初始基準不同而引起的測量誤差的影響，在3 組鋼索形變數據采集前，先以第1 組中的第1 根鋼索按上述步驟1 設定的初始基準進行數據的采集，而在進行其它鋼索數據采集時，可分別通過繩輪兩端鎖緊螺母的調節，使其初始基準分別與第1 根鋼索初始基準的設定值相等，這樣就確保了3 組鋼索測量的初始工作長度都相等。

2.4 數據分析

在分別對繩輪轉角60°與180°處以5 min、2 h、5 h 和24 h 間隔加載保壓的鋼索形變行為研究時，經觀察：在給定預緊載荷作用下，以超過24 h間隔加載保壓，鋼索形變基本不再發生變化。因而為便于分析，將以24 h 間隔測定的數據作為其它間隔加載數據的標準，則以上述時間間隔加載保壓方式下，3 組鋼索測控點預緊載荷與主動繩輪轉角偏差關系如圖4 所示。

從圖4 可以看出，受鋼索絲、股及繩輪間摩擦力作用、轉角及蠕變等因素影響，不同間隔時間加載方式下，即使預緊載荷相等，對應的轉角偏差也不相等。 3 組鋼索存在著隨間隔加載時間的增大，轉角偏差與對應的預緊載荷間的變化曲線都呈現逐漸接近標準曲線，且變化率逐漸變小的趨勢，這說明鋼索穩定性能逐步提高，在裝配中易獲得較高精度。 另外，通過對每根鋼索不同時間間隔對應的4 條曲線變化規律分析還可發現，在相等預緊載荷作用下，加載間隔時間越短，3 組鋼索對應的轉角偏差就越大，間隔時間越長，轉角偏差就越小，越接近標準值。 這主要是因為連續加載間隔時間短時，鋼索發生的主要為彈性形變；隨著間隔加載保壓時間的增大，鋼索蠕變、絲、股及繩輪間微動摩擦等因素的影響逐步增大，導致鋼索松弛而產生張力損失，從而測定的數據減小；但超過24 h 后，因鋼索內部絲、股間結構重新排列均勻，相互間基本不再產生滑移及蠕動磨損現象，致使鋼索內部張力基本不再發生變化，對應的形變也基本保持穩定。

通過對比圖4 的3 組結果可以看出，未經預張拉的鋼索第1 組與經預張拉的第2、3 組相比，不同時間間隔間內其轉角偏差隨預緊載荷變化波動范圍相對較大。 這主要因為預經張拉的鋼索，其內部殘余應力得到大部分消除及絲、股間排列變得較均勻，性能較穩定，而未預張拉的鋼索，不僅性能穩定性較差，而且還產生較大結構伸長，經計算其結構伸長率達0. 2%，如果直接用于鎖系對接，必定會對其裝配及傳動精度產生較大的影響。 而另外經預張拉的兩組繩索結構伸長并不明顯，相等預緊載荷作用的形變雖所區別，但相差不大，經計算最大誤差不超過10%，這主要受鋼索本身的物理特性及結構差異造成的。

圖4 轉角60°和180°處3 組鋼索形變與預緊載荷變化規律Fig.4 Law of deformation and preload in three groups of cables at 60 ° and 180 °

此外，從圖4 中還可看出，不同轉角對鋼索形變也有一定的影響，在測控點預緊載荷相等條件下，呈現轉角越大，對應的轉角偏差反而越小的現象。 這主要因為施加的載荷在從主動繩輪鋼索固定端經鋼索傳遞到預緊載荷測控點過程中，隨著主動繩輪轉角的增大，鋼索與繩輪間接觸弧長逐漸變長，相互間產生的摩擦力相應地增大，導致鋼索張力損失相對變大，從而實測值相對變小。 因而，對于鎖系對接過程中的嚙合與鎖緊兩位置，因對應的轉角值不等，為保證對接同步性，應分別對其裝配精度進行控制。

3 形變補償

空間鎖系對接同步性，主要通過裝配過程對鋼索施加一定預緊載荷抵消其驅動過程中的形變來控制。 然而，通過上述分析可以看出，受鋼索加載時間間隔及轉角等因素影響，相同操作條件下，相等轉角偏差對應的預緊載荷并不相等，呈現加載時間越短，預緊載荷就越小，其在標準曲線(24 h)上對應的轉角偏差就越小的規律。 因而相對于標準曲線對應的預緊載荷來講，補償的張力就越大。 隨著間隔加載保壓時間變長，預緊載荷不僅受鋼索微動蠕變的影響變大，而且還受其從主動繩輪鋼索固定端傳遞到測控點過程中的轉角、絲、股與繩輪間摩擦力作用等因素影響而產生損失，導致松弛而引起新的轉角偏差，致使不同間隔加載方式下的轉角偏差曲線并不重合，而且轉角越大越明顯。 例如，對于給定轉角偏差2°在標準曲線上對應的載荷為F3，如果以間隔5 min 進行加載，則鋼索測控點處預緊載荷在達到F0就能即時滿足要求，然而，隨著分別經歷2 h 和5 h 間隔加載保壓，該轉角偏差對應的預緊載荷F1、F2卻逐步增大，分別相對于標準載荷F3的差值，即補償值F3-F1、F3-F2則逐漸變小，相應地，鋼索穩定性能逐漸得以提高。

為預測鎖系裝配過程中不同預緊載荷作用下張力損失補償值，針對上述以不同時間間隔加載方式下測定的經預張拉的第2、3 組鋼索預緊載荷與轉角偏差的平均值，分別在60°和180°轉角處根據其變化規律對其用指數曲線進行擬合，其擬合曲線可統一表示為式(1)：

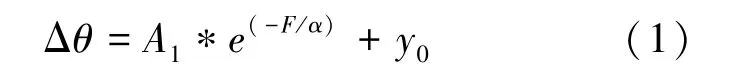
式中，Δθ為轉角偏差(°)，F為預緊載荷(kN)，其它各參數為常數分別見表2。

表2 預緊載荷與轉角偏差擬合方程參數值Table 2 Parameter values of fitting equation between preload and angle deviation

式(1)化簡可得式(2)，即用于預測主動繩輪轉角60°與180°處以上述不同時間間隔加載方式下轉角偏差對應的預緊載荷施加值。

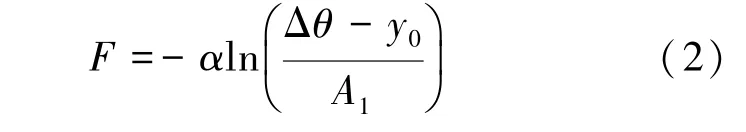
則在轉角偏差Δθ條件下，分別在轉角60°和180°處，以間隔5 min、2 h 和5 h 施加預緊載荷相對于24 h 標準值的差值，即裝配中預緊載荷損失補償值的預測模型可分別表示為式(3)、(4)，經與實測值相比較，兩者誤差在0.1%以內，如表3、表4 所示。

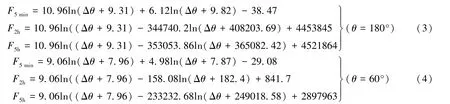
表3 鎖系嚙合位置不同時間間隔加載方式下預測值與實測值比較Table 3 Load comparison between prediction and measured values at meshing position of the locks under different time intervals/kN

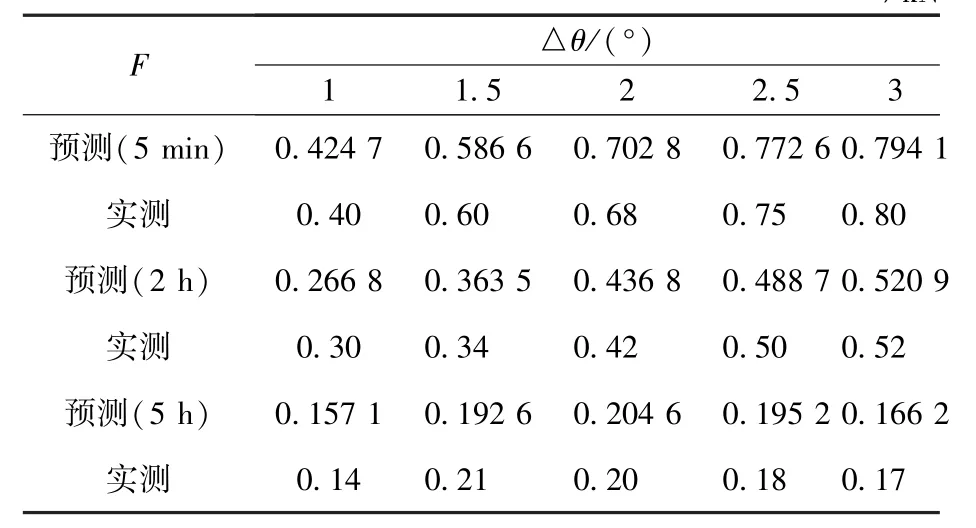
表4 鎖系鎖緊位置不同時間間隔加載方式下預測值與實測值比較Table 4 Load comparison between prediction and measured values at locking position of the locks under different time intervals/kN

4 結論

1)針對空間對接鎖系裝配工況，通過對不同預張拉處理3 組鋼索樣本的試驗研究，建立了不同時間間隔加載方式下以繩輪轉角偏差表示的鋼索形變與預緊載荷間的數學方程，并分析了預處理、不同間隔加載方式和轉角等因素的影響。

2)建立了一個預緊載荷補償的預測模型，該模型能較精確地反映不同時間5 min、2 h 和5 h間隔加載條件下為滿足裝配精度要求所對應的預緊載荷損失補償值，可為鎖系裝配效率的提高提供一定參考。