算法設計思維在人腦與電腦中的研究

摘? 要：自第一臺計算機誕生至今，計算機科學技術發展經歷了數十載，期間取得了頗多成果，但目前還無法定義這門科學的邊界。如今，大數據、云計算、人工智能、“互聯網+”等新問題、新領域、新應用層出不窮，其中許多問題求解都離不開問題的建模和算法的設計與分析。文章就分治策略、動態規劃、貪心法三大經典問題展開算法設計與分析，通過對經典問題的引入、求解、驗證、結論這一完整過程，解析算法設計思維在人腦與電腦中的思維模式以及設計模式，對其差異性和同一性進行研究。

關鍵詞：算法設計;算法思維;問題模型;人腦;電腦

中圖分類號：TP312;TP18 ? ? ?文獻標識碼：A 文章編號：2096-4706（2020）03-0013-04

Abstract：Since the birth of the first computer in 1949，the development of computer science and technology has gone through several decades，during which a lot of achievements have been made，but still no scientist can define the boundaries of this science. Nowadays，big data，cloud computing，artificial intelligence，“internet plus” and other new problems，new fields and new applications keep emerging. In the process of tracing back to the source，many problems cannot be solved without problem modeling and algorithm design and analysis. In this paper，algorithm design and analysis are carried out for three classic problems：divide and conquer strategy，dynamic programming and greedy method. Through the whole process of introducing，solving，verifying and concluding classic problems，the thinking mode and design mode of algorithm design thinking in human brain and computer are analyzed，and the differences and identity are studied.

Keywords：algorithm design;algorithmic thinking;problem model;human brain;computer

0? 引? 言

清華大學出版社出版的《算法設計與分析》作為本校的任選課程教科書之一，是問題求解和程序設計的重要基礎，對學生的邏輯思維和創造性有著重要的作用。本文將對其較為簡單并且重要的內容進行歸納總結，再對算法設計學進行一定的深入討論。

算法是指解題方案的完整而準確的描述，是一系列解決問題的清晰指令，這一系列指令在人腦與電腦中是可以同時存在的。不過，在解決問題時卻有著截然不同的處理方式，人腦利用算法處理問題是通過思想建立模型求解問題，電腦利用算法處理問題是通過程序建立模型求解問題。在運算速度上，如今計算系統中的電腦可以做到每秒萬億次，一般情況下，人腦的計算速度也就勉強做到每秒一次。

但算法的設計不僅僅是依靠電腦進行的，因為完整的算法設計，不僅需要強大的運行速度、存儲空間，更需要人腦的算法思維。這也正是一個算法的優劣可以用空間復雜度與時間復雜度來衡量，而一個算法的成敗可以用人腦思維來控制的原因。

1? 分治策略

分治策略是對于一個規模為K的問題，如果該問題較容易理解分析（如規模K較小）就直接解決，否則將其分解為k個規模較小的子問題，前提是這些子問題之間相互獨立且與原問題形式相同，通過遞歸或非遞歸方法解這些子問題，最后將各子問題的解進行合并，模擬并且得到原問題的解。

1.1? 問題引入

給定n個數，這些數已經按照遞增順序進行排序，要求輸入一個數，如果輸入的數存在于n個數中，返回這個數所在的位置，否則，返回-1狀態碼，表示該數不存在。

1.2? 問題求解

對問題使用分治策略，可以分析出如下求解過程：

（1）將n個數的中位數（如果n為奇數，則向下取整求出中位數）與查找關鍵字比較，如果兩者相等，則查找成功;

（2）若過程1不能匹配成功，則利用中位數所處位置將n個數分成前、后兩半段，如果中位數大于查找關鍵字，則進一步查找前半段，此時后半段可拋棄，反之查找后半段，將前半段可拋棄;

（3）重復以上過程，直到找到滿足條件的記錄，查找成功，返回記錄的關鍵字的位置，或直到無法分段，查找不成功，返回狀態碼-1。

使用C語言程序設計，關鍵代碼如下：

1.3? 問題驗證

根據問題描述，可以進行用例測試。

輸入格式：第一行包括數n，接下來一行是n個遞增的數，最后一行是查找的關鍵字。

輸出格式：關鍵詞的下標。

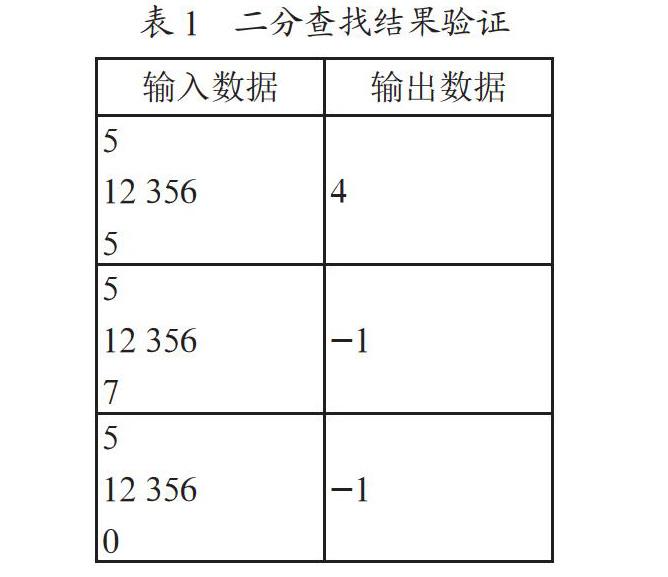
問題驗證過程如表1所示。

1.4? 問題結論

處理分治問題前，需要判斷出其問題性質，判斷其是否符合分治思想的范疇。對于分治策略問題，應該優先考慮下面這么因素：

（1）將原問題的規模縮小到一定程度就可以較為容易地解決;

（2）將規模較大的原問題分解為若干個規模較小的相同問題;

（3）問題所分解出的各個子問題是相互獨立的，即子問題不可再進行分解為新的子問題;

（4）原問題分解出的子問題的解可以合并為原問題的解。

2? 動態規劃

動態規劃從動態性質和規劃性質來說，是Operational Research（簡稱OR）的一個分支，將OR引入時以“運籌帷幄之中，決勝千里之外”為基礎，更名為運籌學。動態規劃實質上是求解決策過程最優化的數學方法。動態規劃也正是為了實現最優化原理，把多階段過程轉化為一系列單階段問題，利用各階段之間的關系，逐個求解。

2.1? 問題引入

設A和B是兩個字符串。下列有3種字符操作，分別是字符的插入、刪除、修改，利用這3種操作將字符串A變為B，求所需要的最少的字符操作次數。

2.2? 問題求解

對問題進行動態規劃，可以分析出如下求解過程：首先建立一個狀態來表示兩個字符串之間的操作情況，假設數組下標從0開始，dp[i][j]表示處理字符串A中的第i+1個與字符串B中的第j+1個字符所需要的步驟，對于每一種操作，都有著對應的模型建立：

（1）插入字符：假設字符串A為ac，字符串B為abc，現在需要在A中插入一個字符b，轉化為處理狀態即為dp[2][2]=dp[2][1]+1，對應的處理情形就是將字符串A變為abc;

（2）刪除字符：假設字符串A為ac，字符串B為abc，現在需要在B中刪除一個字符b，轉化為處理狀態即為dp[2][2]=dp[1][2]+1，對應的處理情形就是將字符串B變為ac;

（3）修改字符：假設字符串A為adc，字符串B為abc，現在需要在A中修改字符d為b，轉化為處理狀態即為dp[2][2]=dp[1][1]+1，對應的處理情形就是將字符串A變為abc;

（4）不做更改：假設字符串A為abc，字符串B為abc，轉化為處理狀態即為dp[2][2]=dp[1][1]=dp[0][0]。

不過首先應該對其進行初始化，將dp[i][0]=i，dp[0][j]=j，最后得到的操作次數應為dp[a][b]，其中a，b分別代表字符串A，B最后一位字符表示的下標加1，初始化時將dp[][]的范圍在字符串A或字符串B的最大長度加1。

2.3? 問題驗證

根據問題描述，可以進行用例測試。

輸入格式：輸入兩個字符串。

輸出格式：輸出一個數值，表示最小的變化次數。

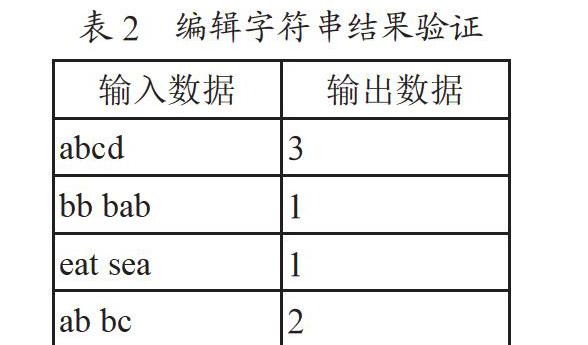
問題驗證過程如表2所示。

2.4? 問題結論

處理動態規劃問題前，需要判斷出其問題性質，判斷其是否符合動態規劃思想的范疇。對于分治策略問題，應該優先考慮以下因素：

（1）問題中的狀態滿足最優化原理：無論其初始狀態和初始選擇如何，對前面的決策所形成的狀態而言，剩下的諸決策接著構成最優策略，即一個最優化策略的子策略也要達到最優化;

（2）問題中的狀態滿足無后效性：下一步驟的狀態只與當前狀態有關，而和之前產生的狀態無關，每個狀態都是過去歷史的一個完整總結;

（3）子問題的重疊性：動態規劃是一種以空間復雜度換時間復雜度的技術，在實現的過程中將存儲產生過程中的各種狀態，所以需要更多的空間，處理過程中會不可避免地將子問題重疊。

3? 貪心算法

貪心算法是指在對問題求解時，放棄從整體最優角度考慮，做出在當前判斷是最好的選擇，最后得到的結果是在某種意義上的局部最優解。

3.1? 問題引入

給一個n個點m條邊的無向圖，求點s到點t的最短路徑的大小，并且將路徑打印出來。

3.2? 問題求解

對問題進行貪心算法（又稱Dijkstra算法），該算法能達到整體意義上的最優解，也方便對其進行理解，可以分析出如下求解過程：

（1）引入一個輔助動態數組（vector）V，它的每個元素V[i]表示當前所找到的從源點v到其他每個頂點vi的長度;

（2）V的初始狀態為：若從v到vi存在連通邊，則V[i]為從v到vi的邊的權值;否則置D[i]為∞;

（3）從源點v到下一個頂點的最短路徑長度所對應的頂點，且這條最短路徑長度僅次于從源點v到頂點vj的最短路徑長度;

（4）V為已求得的從源點v出發的最短路徑長度的頂點的集合，則可證明：下一條次最短路徑（設其終點為e）要么是從頂點v到頂點e，或者是從源點v出發，中間經過V中的頂點而最后到達頂點e的路徑。

使用C語言程序設計，關鍵代碼如下：

3.3? 問題驗證

根據問題描述，可以進行用例測試。

輸入格式：第一行包括數n，m，s，e，分別表示為圖的頂點數、邊數、開始點、結束點，后m行，由n1，n2，l組成，表示n1，n2兩點之間存在路徑，長度為l。

輸出格式：第一行輸出從開始點到結束點的距離，第二行顯示路徑。

問題驗證過程如表3所示。

3.4? 問題結論

處理貪心問題前，需要判斷出其問題性質，判斷其是否符合貪心思想的范疇。對于貪心問題，應該優先考慮以下因素：

（1）貪心算法適用于求解最優化問題;

（2）算法的正確性證明方法包括數學歸納法和交換論證法;

（3）求解過程是自頂向下，先做貪心選擇，然后將規模較大的子問題歸約為規模更小的子問題;

（4）如果貪心算法得不到最優解，可以對問題的輸入進行分析或者估計算法的近似比;

（5）通常對原始數據排序之后，貪心算法是一輪處理，時間復雜度和空間復雜度低。

4? 算法、人腦、電腦間的關系

如果將三者結合在一起運用，可以解決目前已知的任何難題，因為在自然科學中，問題的產生其實就是這一過程。其中，先從人腦開始討論，人腦的功能主要可概括為記錄、整合、分析、傳播，理論上人腦的功能是無上限的，但是存在的弊端就是被現實所阻擋。此時，可以將這一過程交付給電腦，人腦依靠思想架構，電腦也是如此，在人腦與電腦的關系上做到有機的整合。這種整合就又涉及到算法，算法即模型，通過摩爾定律可知，未來的算法價值將會更大。

正如上文所寫的內容一樣，人們在規范問題時，不是以人腦某種思考角度直接命名，也不是以電腦某種程序角度直接命名，而是將其歸結為算法命名。其實還有更多的算法，如回溯法、線性規劃、網絡流算法、近似算法、隨機算法、量子算法等，這些已經存在的算法內容更為復雜，也是人腦和電腦共同編譯產生的結果。

5? 結? 論

人腦思維的模型構建，為算法設計提供了清晰的指令，而電腦軟硬件的更新迭代，為算法實現提供了更大的運行空間。但隨之而來的是三者的同步問題，為此有必要以一種有效的連接方法將人腦、電腦、算法進行整合，防止不同步驟下會產生失敗的結果，以此保證問題得以正確解決。至此，本文僅介紹了幾種算法模型，給出了人腦的思維過程和電腦的編碼過程，在后期隨著知識的積累將對其進行進一步的深入研究。

參考文獻：

[1] 屈婉玲，王捍貧，段莉華.面向軟件工程學科的算法課程建設 [J].中國大學教學，2012（12）：55-57.

[2] 劉家銘.基于大數據背景下的數據安全分析 [J].現代信息科技，2019，3（18）：129-130.

作者簡介：劉家銘（1999-），男，漢族，江西南昌人，本科在讀，研究方向：軟件工程。