基于矩陣分解的超奈奎斯特接收技術

蘇鳳軒

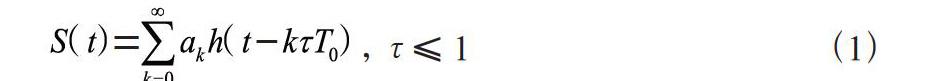
摘? 要：通信傳輸系統中引入超奈奎斯特信號進行傳輸時，對碼間干擾等問題進行了研究。為了降低碼間干擾，提出了利用基于矩陣分解的方案消除超奈奎斯特碼間干擾用以提高系統傳輸的性能。該方案運行時獨立于網格狀態，首先在發射端處采用相應預編碼進行降低干擾，其次在接收端處利用分解進一步消除干擾，消除干擾后的信號通過相關信道譯碼，最后利用硬判決恢復出原始信息。仿真驗證結果表明，基于矩陣分解的FTN傳輸系統可以進一步提高系統的性能。

關鍵詞：超奈奎斯特;碼間干擾;矩陣分解;預編碼

中圖分類號：TN911.4? ? ? 文獻標識碼：A 文章編號：2096-4706（2020）03-0047-03

Abstract：When the Faster-Than-Nyquist signal is introduced in a communication transmission system for transmission，the existence of inter-symbol interference and other issues are studied. In order to reduce the existing inter-symbol interference，a solution based on matrix factorization is proposed to eliminate the inter-symbol interference of Faster-Than-Nyquist to improve the performance of the? system transmission. The scheme is independent of the ISI grid state. First，the corresponding precoding is used at the transmitter to reduce interference，and then is to use the decomposing at the receiver to further eliminate interference，and the signal after interference is decoded through the relevant channel. Finally，the original information is recovered by using the hard decision. Simulation results show that the Faster-Than-Nyquist transmission system based on matrix decomposition can further improve the system performance.

Keywords：FTN;ISI;matrix decomposition;precoding

0? 引? 言

作為5G的候選技術，FTN信號因其高頻譜效率而受到越來越多的關注[1]。1970年，Mazo提出超奈奎斯特（Faster- Than-Nyquist，FTN）的概念，表明了傳輸速率比奈奎斯特所定義的更快，同時系統的誤碼性能也不會降低。奈奎斯特強調信號的正交性以避免符號間干擾，FTN引入的碼間干擾（Inter-Symbol Interference，ISI）進行非正交傳輸，導致犧牲帶寬效率來維持正交性。

為了解決這個問題，已經提出了很多關于FTN信號接收端的檢測方案，其中最為經典的算法就是最大似然序列估計[2]（Maximum Likelihood Sequence Estimation，MLSE），但其復雜度極高。已知提出的M-BCJR算法是通過選擇網格解碼來降低接收端檢測的復雜度，其復雜度依舊很高。因此，針對超奈奎斯特干擾消除問題提出了一種基于矩陣的相關算法，分別提出了基于QR分解和基于矩陣上下三角分解的算法。基于矩陣的算法是利用矩陣相關計算來消除碼間干擾。最后的仿真結果也表明了基于矩陣算法的檢測方案性能優于基于網格解碼的方案。但是上述所提出的矩陣相關算法忽略了數據幀之間的干擾，因此其性能還有待提高。

針對以上問題，本文提出了一種新的關于超奈奎斯特碼間干擾消除的方案：首先發射端采用預編碼以及信道編碼后的符號經過調制后插入循環前綴，其次根據預編碼矩陣與干擾矩陣H之間的關系對發送端的信號降低干擾;接收端進行相關分解，使得ISI被完全消除。同時，本文提出的方案是獨立于ISI網格解碼[3]，無需考慮網格解碼的計算。最后將本文提出的方案分別與其他方案進行仿真分析比較。

1? 系統模型

1.1? FTN系統模型

對于基帶信號的線性調制h（t）的FTN傳輸系統，其發送端信號可表示為：

式中，S（t）表示接收信號，ɑk表示符號信息。對于FTN信號，每個符號的時間間隔Ts=τT0（0<τ<1），τ表示符號壓縮因子。

與正交傳輸不同之處在于FTN傳輸系統存在一個符號壓縮因子τ，使得發送信號的速率變得更快。當τ<1時，ISI隨著τ值變化，傳輸速率越大，τ值越小，導致引入的ISI也越嚴重。當τ=1時，傳輸的正交信號在接收端不受ISI的影響。

根據以上所述，本文提出基于矩陣分解消除ISI的FTN系統框圖，如圖1所示。信號首先進行信道編碼，編碼后的信號再進行調制，之后插入的循環前綴（Cyclic Prefix，CP）合成幀結構。此結構可以有效阻隔數據幀之間受到的干擾。然后再經過預編碼用以降低發送端信號的ISI，最后經過FTN成型濾波器后得到符號間隔為τT0的FTN傳輸信號，實現發送端的FTN傳輸。

接收端接收到的信號首先經過FTN匹配濾波器，隨后對信號以τT0的符號間隔進行下采樣，經過分解后消除ISI的同時去除循環前綴再進行譯碼，最后恢復出原始信息。

FTN傳輸模型中，接收端接收到的信號序列表示為：

rm和? 分別表示接收端的第m個采樣信號以及高斯白噪聲w（t）經過匹配濾波器之后所引入的噪聲序列。在FTN信號中，檢測第k個符號ak時會受到前一個符號ɑk-1和后一個符號ɑk-1的干擾，且干擾符號的數量是由τ值而決定。因此可以得到h-1和h1是第一干擾系數，其值相等，以相同的方式得到，h-2和h2是第二干擾系數，其值相同，以此類推得到其他的干擾系數。

接收信號R由濾波器系數和傳輸的數據符號卷積所表示。對于一般的結構，接收信號經過匹配濾波器和采樣后輸出以矩陣形式表示為：

1.2? 基于矩陣特征分解的預編碼和分解

由上述分析可以得到，在高斯信道中進行FTN傳輸時，受到的符號間干擾由FTN產生的，且干擾用矩陣H表示。另外，添加的循環前綴阻隔了數據幀之間的相互干擾。因此本文提出了一種簡單且性能較好的符號間干擾消除方案。

在發射端，信號序列通過預編碼矩陣UH得到：

2? 性能分析和仿真結果

本文將提出的方案與其他方案分別在高斯信道中進行仿真分析比較。選取滾降衰落因子系數為β=0.3的根升余弦成型脈沖。

本文提出的算法相比其他算法，在發送端添加了循環前綴以阻隔數據幀之間的干擾，其長度S大于因FTN引入ISI長度和的一半。仿真過程中以QPSK（τ=1）調制的性能為參考，選取符號采樣率是1 Hz，設置幀的長度L為1 024，濾波器的邊帶長度為10。在仿真過程中利用高斯信道，描繪了當時間壓縮因子τ分別取0.90和0.82時，同等條件下的仿真圖。

圖2和圖3顯示了在高斯信道中當（τ=0.90）和（τ=0.82）時，基于QR分解和M-BCJR方案的誤碼性能與本文提出方案的FTN傳輸誤碼率圖。當（τ=0.90），RSN大于8時，基于QR分解方案的性能優于M-BCJR的算法。在τ=0.90，RSN=10時基于QR分解方案比M-BCJR的方案有大約0.3 dB的增益，此時，本文提出的方案性能比基于QR分解的方案大約有0.5 dB的增益，與M-BCJR的方案相比大約有0.7 dB的增益。當τ=0.90時，本文提出的方案誤碼性能曲線與τ=1.00時相接近，且誤碼性能可以達到10-5至10-6之間，

由兩圖對比可知，一方面，隨著τ值的減小，FTN引入的ISI也會越嚴重，其系統誤碼性能也會隨之變差，但是本文提出的方案系統性能始終優于其他方案;另一方面，系統為了有更好的誤碼性能，其τ值不宜過大或過小。

3? 結? 論

FTN信號提高了傳輸速率，但是也引入了不可避免的ISI，因此本文提出了一種基于矩陣的特征分解得到預編碼和分解矩陣，避免了需要考慮ISI的網格狀態與ISI抽頭組之間的大小關系。最后通過仿真分析對比，得出本文提出的方案對系統的誤碼性能有著很大的改善。

參考文獻：

[1] BANELLI P. Modulation Formats and Waveforms for 5G Networks：Who Will Be the Heir of OFDM？：An overview of alternative modulation schemes for improved spectral efficiency [J].Signal Processing Magazine，IEEE，2014，31（6）：80-93.

[2] FORNEY，G，JR. Maximum-likelihood Sequence Estimation of Digital Sequences in the Presence of Intersymbol Interference [J].IEEE Transactions on information Theory，1972，18（3）：363-378.

[3] BEDEER. E，AHMED M.H，YANIKOMEROGLU H.A Very Low Complexity Successive Symbol-by-symbol Sequence Estimator for Faster-than-Nyquist Signaling [J].IEEE Access，2017（5）：7414-7422.