基于格型結構LMS算法的自適應預測

摘 要：自適應預測在語言和圖像編碼中有著大量的應用。本文重點研究LMS算法的一步線性預測。其間推導了LMS算法在格型結構中的表達式，并驗證了二階格型結構的LMS算法收斂過程，也在格型結構系統中驗證了LMS算法在一步前向預測上的準確性。結果表明，在格型結構中使用LMS算法進行一步前向預測，能夠達到較高的準確性。

關鍵詞：LMS算法;格型結構;自適應預測

中圖分類號：TN713 文獻標識碼：A 文章編號：1003-5168（2020）13-0014-03

The Adaptive Prediction Based on Lattice Structure LMS Algorithm

LYU Xiaona

（Zhengzhou Business University，Zhengzhou Henan 451200）

Abstract： The adaptive prediction has a lot of applications in language and image coding. This paper focused on the one-step linear prediction of LMS algorithm. In the meantime， the expression of the LMS algorithm in the lattice structure was derived， and the convergence process of the LMS algorithm of the second-order lattice structure was verified， and the accuracy of the LMS algorithm in one-step forward prediction was also verified in the lattice structure system. The above verification shows that using the LMS algorithm for one-step forward prediction in the lattice structure can achieve higher accuracy.

Keywords： LMS algorithm;lattice structure;adaptive prediction

自適應預測是利用一段已知的數據來估計這一段之外的數據，如果估計的數據在這一段數據之前稱為后向預測，如果估計的數據在這一段數據之后稱為前向預測。在語言和圖像編碼中，線性預測有著廣泛的應用。線性預測編碼（LPC）就使用了線性預測的方法。

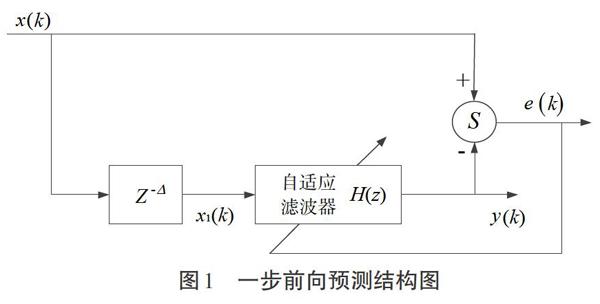
本文主要研究在格型結構中使用LMS算法進行一步前向預測（見圖1）的原理及方法。在自適應算法中，LMS最大的優點是算法簡單，實現容易。格型結構各階參數是解耦的，互相之間并不影響。在自適應迭代過程中，相比于滑動自回歸系統來說，收斂速度有一定的優勢。本文研究了格型結構中LMS算法的計算原理，并在二階條件下驗證了LMS算法的收斂過程。同時，驗證了單頻信號在跳變過程中的預測過程，可以看出，在格型結構中，LMS算法能夠得到較好的預測結果。

1 基本理論

滑動自回歸系統在時不變系統中有特殊的優點。但在自適應過程中，當一個參數被調整之后，所有的零點或極點都會發生變化。為了降低參數的改變對零、極點的影響，系統往往使用格型結構。格型結構有全零點格型結構、全極點格型結構和零極點格型結構。格型結構應用最多的是全零點格型結構和全極點格型結構。全零點格型結構和全極點格型結構屬于級聯性的，并且可以保證在調節參數時只改變對應級的零極點。由于格型結構的優點，其在自適應濾波以及線性預測等方面有大量的應用。

本文使用全零點格型結構，通過最小均方算法（LMS）進行一步前向預測。全零點系統沒有極點，對應的格型結構如圖2所示。全零點系統的標準模式如式（1）所示[1-3]。

LMS算法的代價函數使用均方誤差，均方誤差屬于統計量，實際情況下，輸入信號是順序輸入的，要獲得統計意義上的均方誤差，需要等信號全部輸入完畢才可以獲得估計值。要根據部分輸入來獲得統計意義上的均方誤差是不現實的，所以LMS計算就使用單次采樣數據的均方誤差來代替統計均方誤差。根據單次數據均方誤差，可得代價函數的梯度估值，如式（3）所示。

式中，Xk和Wk為第k步迭代時的輸入信號向量和對應的權向量;[X*k]為[Xk]的共軛向量，若輸入信號為實信號，則二者相等。LMS算法沿著負梯度方向收斂，故權值收斂方式如式（4）所示。

式中，[μ]為迭代的步進參數，[μ]的大小決定了迭代的穩定性。當[μ]的取值超過一定值時，迭代過程會發散，其取值范圍如式（5）所示。

式中，[λmax]為對應輸入信號相關矩陣的最大特征值，即輸入信號解耦后的最大功率值。

圖2的格型結構前后兩級相對獨立，LMS算法是基于均方誤差的，所以假設以下三種相關函數。

根據參考文獻[3]，可知每一級的權向量為：

每一級輸出值的均方值對對應級權向量的梯度估值為：

所以，圖2所示的格型LMS算法如式（11）所示。

式中，[μl]為每一級格型結構的步進迭代值。

2 試驗結果及分析

2.1 二階格型結構迭代過程

一步前向預測系統的結構圖如圖1所示，一步前向預測的目的是通過過往的數據預測下一個數據。自適應預測器在干擾對消和譜線增強等領域都有廣泛的使用。格型結構可以保證在迭代過程中，每一級的參數調整不影響其他參數。為了便于觀察迭代過程，本文選擇二階對稱格型結構。

預測系統往往針對有噪輸入信號，所以最終預測值會有一定的誤差，但誤差值會在一個較小范圍內徘徊。若輸入信號是無噪，經過迭代預測值的誤差會減小到0。二階格型結構的系統函數如式（12）所示。

在二階格型結構中，使用[x（k-1）]和[x（k-2）]來預測[x（k）]。設分別由[x（k）]、[x（k-1）]和[x（k-2）]所構成的相關矩陣為：

由圖2和式（6）、式（7）、式（8）可知，代價函數為：

根據式（9），可得二階最佳權系數分別為：

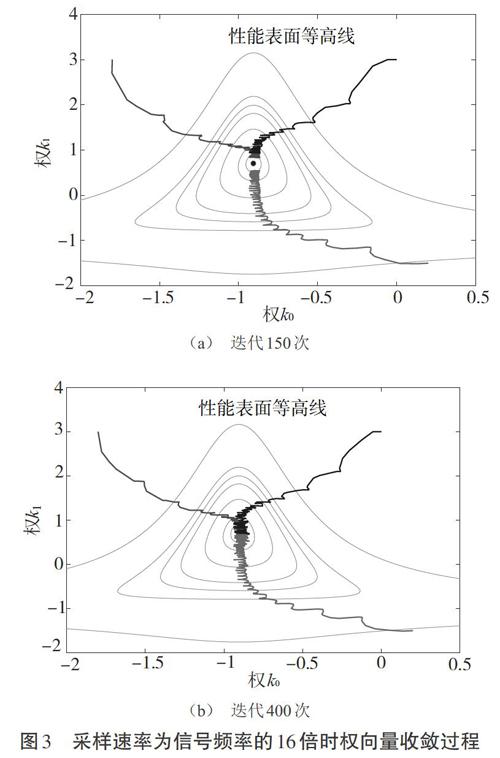
將圖2中的格型結構替代圖1中的自適應濾波器，就可以得到一步預測濾波器。通過一步預測濾波器可以由過往的[x（k）]值預測[x（k）]的下一個值。這里設輸入信號為正弦信號的16倍采用速率。由式（13）和式（16）可以計算最佳權值系數[k0opt]為-0.906，而[k1opt]為0.708。圖3為上述情況的仿真結果，其中，圖3（a）為迭代150次的收斂過程，圖3（b）為迭代400次的收斂結果。圖3中的閉合曲線為誤差曲線，一般的誤差代價函數為二次多項式，對應的誤差曲線為橢圓，但二階格型結構的誤差代價函數不是二次多項式，所以對應的誤差曲線并不是橢圓。圖中的誤差從中心向外依次對應的誤差值為0.05、0.06、0.1、0.16、0.2、0.25和0.6。

由圖3（a）可以看出，三個初始權向量分別從[-1.8，3.0]、[0，3]和[0.2，-1.5]起始位置出發，通過150次的迭代，三條收斂曲線都達到了誤差值優于0.05的范圍內。而由圖3（b）可以看出，通過400次的迭代，三條收斂曲線都到達了最優點附近。這時的誤差主要由輸入信號中引入噪聲所帶來的。通過圖3可以看出，只有經過一定步數的迭代，不管[k0]和[k1]的初始取值從哪里開始，最終都會收斂到最佳權值位置。當然，由于輸入信號中引入的噪聲，最終只能收斂到最佳權值附近，并在最佳權值附近徘徊，而徘徊的幅度由噪聲的功率值決定。

由圖3可以看出，使用LMS算法進行迭代，隨著迭代步數的增加，權向量最終都會收斂到最優權向量位置。當然，由于輸入信號的隨機性，迭代后的權值會在最優權向量附近徘徊。

2.2 一步前向預測效果

圖4為一步前向預測的結果，其中，輸入信號為三種不同頻率、不同幅度的信號依次輸入時的預測效果。圖4（a）是輸入信號和預測后的輸出信號;圖4（b）為預測值與輸入值之間的誤差。通過圖4可以看出，當輸入信號由一個狀態切換到另一個狀態時，對應的誤差較大，隨著迭代過程的發展，誤差越來越小。在每次輸入信號狀態切換后，大約經歷50次迭代后，預測值與輸入值兩者就有較好的吻合。

3 結論

本文通過分析自回歸結構和格型結構，導出自回歸結構與格型結構的關系，同時導出格型結構下輸出端對格型系數的梯度關系。為了清晰展現LMS算法的收斂過程，本文選擇二階格型結構進行迭代收斂過程的仿真，即給出了格型結構各級輸出對應的代價函數，同時給出等誤差曲線。格型結構的代價函數及誤差曲線有別于遞歸及非遞歸結構，誤差曲線并不是橢圓線（這里針對二階結構）。基于上述分析，本文重點仿真了二階格型結構的收斂過程。可以看到，通過一定的迭代步數，不管初始格型結構系數如何選擇，最終都會收斂到最優權系數位置。由于輸入信號包含有隨機成分，所以最后只能收斂到最佳權值附近，并在最佳權值附近徘徊。本文最后通過單頻率變換信號和雙頻率變換信號驗證了格型結構下的LMS算法一步前向預測。可以看到，每當信號變換后，通過一定步數的迭代，預測的結果就能達到一定的準確度。

通過本文的分析，格型結構下LMS算法的收斂效果比較明顯，只要迭代步數充足，最終都能收斂到較優的狀態。通過LMS進行一步前向預測，也可以得到較為準確的預測結果。使用LMS算法的缺點主要在于需要的迭代步數較多，同樣條件下需要的收斂時間較長。后續根據信號和系統的特殊性，改變迭代系數，獲取更優的收斂速度。

參考文獻

[1]威德羅.自適應逆控制[M].西安：西安交通大學出版社，2000.

[2]胡廣書.數字信號處理-理論、算法與實現[M].北京：清華大學出版社，2012.

[3]沈福民.自適應信號處理[M].西安：西安電子科技大學出版社，2002.

收稿日期：2020-04-12

作者簡介：呂小納（1984—），女，碩士，助教，研究方向：信號處理、神經網絡。