基于Heaviside過濾的多相材料拓撲優化設計
曹浩 彭羅


摘 要:為解決以柔順度最小化為目標的多相材料結構拓撲優化問題,提出了一種新的拓撲優化求解方法。首先,基于RAMP方法和Heaviside過濾函數形成設計變量和物理變量,構建以柔順度為目標的多相材料結構拓撲優化模型及近似優化模型;然后,采用榮見華等提出的改進交替主動相算法,最后,采用MMA求解器優化求解。給出的算例結果表明,與現有方法相比,該方法可以得到更優的拓撲解,并解決多相材料結構單元幾種材料并存的問題。
關鍵詞:Heaviside過濾;交替主動相;MMA求解
中圖分類號:TB34文獻標識碼:A文章編號:1003-5168(2020)13-0055-03
Topological Optimization Design of Multiphase
Materials Based on Heaviside Filtering
CAO Hao PENG Luo
(School of Automotive and Mechanical Engineering, Changsha University of Science and Technology,Changsha Hunan 410076)
Abstract: In order to solve the topology optimization problem of multiphase material structure with the objective of minimizing the flexibility, a new topology optimization method was proposed. Firstly, based on the RAMP method and the Heaviside filter function, the design variables and physical variables were formed, and the topological optimization model and the approximate optimization model of the multiphase material structure with the flexibility as the goal were constructed. Then, the improved alternating active phase algorithm proposed by Rong Jianhua and others was used, and finally, the MMA solver was used to optimize the solution. The results show that compared with the existing method, this method can get better topological solution and solve the problem that there are several materials coexisting in the multiphase material structure element.
Keywords: Heaviside filtering;alternating active phases;MMA solution
1 研究背景
在解決多相材料結構單元幾種材料并存的問題時仍存在一定的難度。在單相材料拓撲優化中,為減少結構拓撲中存在的一些中間密度單元或灰度單元,Guest等首先提出了采用Heaviside函數進行過濾的方法[1]。之后,Sigmund在改進的Heaviside密度過濾方法基礎上提出了基于形態學的過濾方法,該類方法都能獲得0/1分布較為清晰的優化結果[2]。Sigmund采用密度過濾和Heaviside密度映射對柔性機構進行優化,獲得了清晰的結構拓撲[3]。Cui等提出用Heaviside閾值函數解決多相材料結構單元有幾種材料并存的問題[4]。在設計變量變化較大時,結構的性能指標出現較大跳躍,導致出現求解振蕩問題。
2 多相材料插值模型
為了獲得清晰的結構拓撲優化解,采用Guest等[5]提出的光滑Heaviside函數,將單元設計變量[ρsi]形成物理變量場[ρsi],使用物理變量[ρsi]進行結構有限元分析。
根據Zhou等[6]提出的RAMP材料插值模型,提出改進的RAMP材料插值模型,構建單元剛度矩陣的表示式:
式中,[v]為經驗參數,取值為6;[Ki]表示當[m]相實體材料的物理變量為[ρsi]時第[i]號單元的剛度陣;[K0i]表示單元的彈性模量為1.0時第[i]號單元的剛度陣;[Emin]表示一個極小的值。
結構中任意的設計單元有
本文以結構柔順度最小化為目標,實體材料體積為約束的多相材料結構拓撲優化模型近似表示為式(4):
式中,[Cρ]表示結構柔順度;[V(0)]表示初始設計的結構體積;[Vk+1s]表示第[k+1]步第[s]相材料的體積限,計算公式為:
式中,[γ1]取0.01(本文中所有算例);[Vk+1s]相對于外循環迭代步數[k]是單調變化的,從而確保有限迭代步后,[β]為曲率參數[β]變化后的第一迭代步的迭代步編號的集合;[V(k)]表示第[k]迭代步設計的結構體積。
3 目標函數和體積的靈敏度分析
結構的任意性能函數[f(ρ)]對設計變量[ρsi]的導數可表示為:
目標函數結構柔順度對設計變量[ρsi]的一階導數為:
對于任意相實體材料體積對設計變量[ρsi]的一階導數表示式:
4 改進的交替主動相算法及求解優化
Tavakoli等[7]提出交替主動相方法解決多相材料的求解問題,之后俞燎宏等[8]改進交替主動相算法。本文引用俞燎宏等人的交替主動相算法進行優化求解,用[a]和[b]分別表示這兩相主動相材料[[a=1,2,…,m];[b=a+i(i=1,2,…,m-a)]],則將式(3)轉化為:
設[yq=x(a-1)×N+i],將[ρai=x(a-1)×N+i]作為主動設計變量,[ρbi=x(b-1)×N+i]作為從動設計變量,其他變量不變。從動設計變量可以看作是主動設計變量的函數,由式(10)得:
將優化模型式(4)的求解轉化為式(13)二元相拓撲優化子模型的求解。
最后可采用MMA算法對子模型式(13)進行求解,然后,循環此過程,直到[r=m(m-1)/2]。取[ρsi=x(k+1),m(m-1)/2(s-1)×N+i]更新設計變量,完成一次內迭代循環。
5 優化算例
采用本文提出的Heaviside函數拓撲優化方法解決多相材料結構單元有幾種材料并存的問題,設計域如圖1所示。邊界條件為:左邊固定約束,右邊下端點作用一個垂直向下的載荷[F=1],泊松比[ν]=0.3。初始設計域被離散成4 608(長[L]=96個,寬[H]=48個)個四節點平面單元,過濾半徑[rmin=3.0?]([?]是結構單元邊長的最小尺寸)。
假設結構由2相實體材料和1相空洞材料組成。第1相和第2相實體材料的彈性模量分別為1和2,第3相材料(空洞材料)的彈性模量設為[1.0e-9]。第1相和第2相實體材料目標體積比分別預定為15%和25%。此算例中,體積指數[αv]取1.025,體積約束限參數[γ1]取0.01,收斂參數取[ε1=0.01]。
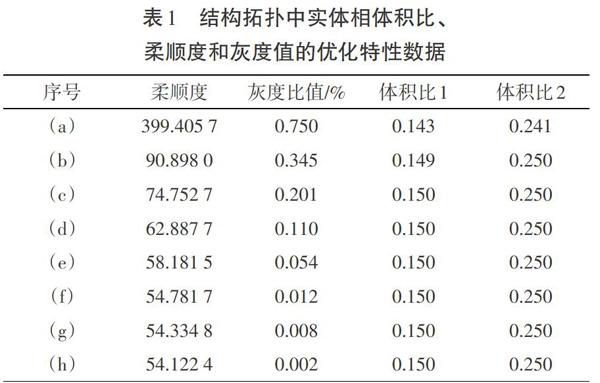
表1給出了實體相體積比、柔順度和灰度值的優化特性數據,由表1中灰度比值可知,構型黑白比轉化為0.002,已經達到了0/1分布的要求,拓撲構型清晰度已經非常清晰了。圖2給出了柔順度和實體相體積的優化歷程曲線。
優化歷程曲線
圖3是分別采用本文方法和Tavakoli R等人提出的[7]方法求解優化問題時獲得的局部最優結構拓撲圖以及其最小柔順度值。從圖3可知,由本文方法優化得到的最后的拓撲構型,實體相構型邊緣呈鋸齒狀,表明已得到非常清晰的拓撲構型。
6 結論
本文針對多相材料拓撲優化問題,提出了一種新的解決多相材料結構單元幾種材料并存的問題的結構拓撲優化求解方法。通過本章理論推導和數值算例驗證,確定了本文方法的可行性。本文提出一個新的靈敏度過濾Heaviside函數,引入改進的RAMP插值函數使得拓撲結構能穩定收斂到最優解。采用本文方法分別對三相材料進行拓撲優化,對比現有文獻方法,得到更優的拓撲優化解。本文方法很好地解決了多相材料拓撲構型不清晰的問題,并獲得較好的結構拓撲。
參考文獻:
[1]Guest J K , J. H. Prévost, Belytschko T . Achieving minimum length scale in topology optimization using nodal design variable and projection functions[J].International Journal for Numerical Methods in Engineering,2004(2):238-254.
[2]Schevenels M, Sigmund O. On the implementation and effectiveness of morphological close-open and open-close filters for topology optimization[J]. Structural and Multidisciplinary Optimization, 2016(1):15-21.
[3]Sigmund O . Morphology-based black and white filters for topology optimization[J]. Structural and Multidiplinary Optimization,2007(4-5):401-424.
[4]Mingtao Cui,Yifei Zhang,Xinfeng Yang,et al. Multi-material proportional topology optimization based on the modified interpolation scheme[J]. Engineering With Computers,2018(34):287-305.
[5]王健,程耿東.多工況應力約束下連續體結構拓撲優化設計[J].機械強度,2003(1):55-57,75.
[6]Zhou S,Wang M Y. Multimaterial Structural Topology Optimization with a Generalized Cahn-Hilliard Model of Multiphase Transition[J]. Structural and Multidisciplinary Optimization,2007(2):89-111.
[7]Tavakoli R,Mohseni S M . Alternating active-phase algorithm for multimaterial topology optimization problems: A 115-line MATLAB implementation[J]. Structural & Multidisciplinary Optimization,2014(4):621-642.
[8]俞燎宏,榮見華,唐承鐵,等.基于可行域調整的多相材料結構拓撲優化設計[J].航空學報,2018(9):117-133.
收稿日期:2020-04-08
基金項目:國家自然科學基金 (11772070,11372055);中國建筑第五工程局有限公司科研項目。
作者簡介:曹浩(1994—),男,碩士,研究方向:結構拓撲優化設計;彭羅(1995—),男,碩士,研究方向:結構拓撲優化設計。

