龍門銑床橫梁結構的輕量化設計*

,2

1.陜西理工大學 機械工程學院 陜西漢中 723000 2.陜西省工業自動化重點實驗室 陜西漢中 723000

1 輕量化設計背景

大型龍門銑床是飛機、輪船、汽車等工程領域廣泛應用的一種機械裝備。在實際應用過程中,滑鞍滑座和主軸箱的重力作用及橫梁的自重作用,會使橫梁產生較大的變形,進而可能會嚴重影響機床的加工精度。因此在傳統設計中,龍門銑床橫梁結構較為笨重,剛度冗余較大。減小橫梁的質量,可以降低生產及安裝的成本。如何在滿足剛度要求的前提下減小橫梁結構的質量,對大型龍門銑床的設計提出了新的要求。

目前,在國內外龍門銑床橫梁結構研究中,主要采用優化橫梁結構外形尺寸及內部筋板形狀、尺寸、布局等方法,對橫梁結構進行優化,達到輕量化的目的。茅啟園等[1]通過對橫梁結構進行靜動態計算分析,得出橫梁內部筋板振動是導致橫梁結構加工精度不高的主要原因,并采用響應面優化的方法對橫梁內部筋板的尺寸進行優化,提高了橫梁結構的加工精度。程彬彬等[2]通過對橫梁結構進行靜動態分析,初步確定橫梁結構優化的關鍵尺寸為橫梁外壁厚與筋板厚度,通過靈敏度分析確定最終的設計變量,并通過響應面優化方法對橫梁結構進行了優化。孫芹等[3]對橫梁結構進行靜動態分析,并利用拓撲優化的方法對橫梁內部筋板進行重新布局,優化后橫梁結構整體剛度得到明顯提高,同時實現了輕量化。楊建交等[4]針對橫梁截面尺寸較大導致質量過大的問題,通過正交試驗、靈敏度分析等方法確定了橫梁優化的關鍵尺寸,并采用響應面優化方法對橫梁截面尺寸進行了優化。吳珊等[5]針對銑床加工剛度不足的問題,通過優化立柱內部筋板結構改善了立柱的靜動態特性,從而使機床的加工精度和效率得到明顯提高。Mu等[6]通過拓撲優化方法,將優化目標設置為橫梁結構的整體最大剛度,在保證質量滿足設計要求的前提下,對橫梁結構進行優化,減小了橫梁結構的變形。Zhao等[7]通過應用結構仿生學,研究大葉肋和仙人掌優良的結構與性能,將大葉肋和仙人掌結構特點應用于銑床橫梁結構,使橫梁結構的質量和變形減小。

上述研究雖然考慮了橫梁結構的外形尺寸與內部筋板布局,但是忽略了橫梁結構變化后固有頻率的變化。筆者在龍門銑床橫梁結構三維模型的基礎上,利用有限元方法進行結構靜力學分析,通過響應面優化方法,以橫梁質量為目標函數,以最大變形和結構的一階、二階固有頻率為約束條件,對橫梁結構進行優化。

2 有限元建模

2.1 三維模型

根據龍門銑床橫梁結構的設計尺寸,建立橫梁結構的實體三維模型,如圖1所示。橫梁結構的外形尺寸為6 032 mm×1 315 mm×824 mm,橫梁壁厚為20 mm,端面壁厚為30 mm,內部加強筋厚度為20 mm。橫梁內部共有12條X形加強筋,橫梁前端橫截面為O形。橫梁結構內部布局如圖2所示。

圖1 橫梁結構實體三維模型

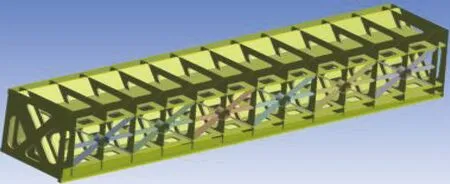
圖2 橫梁結構內部布局

橫梁是薄壁件,橫梁內部有12條X形加強筋、兩個交叉板、兩個上下橫板,板上均有孔。橫梁外部有許多倒圓、倒角、圓孔、小凸臺等。可見,橫梁結構較為復雜。在劃分網格時,以上小特征內部會產生大量有限元單元,進而提高網格劃分的難度。因此,在建模時對橫梁結構進行簡化[8]。

2.2 材料參數

龍門銑床橫梁結構材料采用HT300灰鑄鐵,相關參數見表1。

表1 HT300灰鑄鐵參數

2.3 網格劃分

根據龍門銑床橫梁結構特點,采用四面體法來劃分網格。網格的單元數為384 017,網格的節點數為198 933,網格劃分后模型如圖3所示。

2.4 約束條件

由于橫梁結構是通過兩個立柱支撐的,因此在橫梁與立柱接觸的部位施加全約束邊界條件。

2.5 載荷條件

橫梁結構的受力情況主要來源于三個方面:橫梁結構自重、滑鞍滑座及主軸箱的重力、切削力[9]。橫梁結構的自重可以通過在整體結構上施加重力加速度來模擬,滑鞍滑座及主軸箱的重力根據實際情況,設置為40 000 N。

圖3 橫梁結構網格劃分后模型

在實際切削加工時,如果采用圓柱銑刀,刀具材料為硬質合金,工件材料為灰鑄鐵,那么主切削力F為[10]:

(1)

式中:ae為銑削寬度,ae=90 mm;fz為每齒進給量,fz=0.16 mm/Z;ap為銑削深度,ap=8 mm;z為總齒數,z=10;d1為銑刀直徑,d1=100 mm。

通過計算得到主切削力F為9 557 N,且Fy=0.76F=7 263 N,Fx=0.8F=7 647 N,Fz=0.36F=3 440 N。Fx為作用在龍門銑床主軸上的軸向力,Fy為沿豎直方向進給的分力,Fz為沿水平方向進給的分力,橫梁結構受力分析如圖4所示。

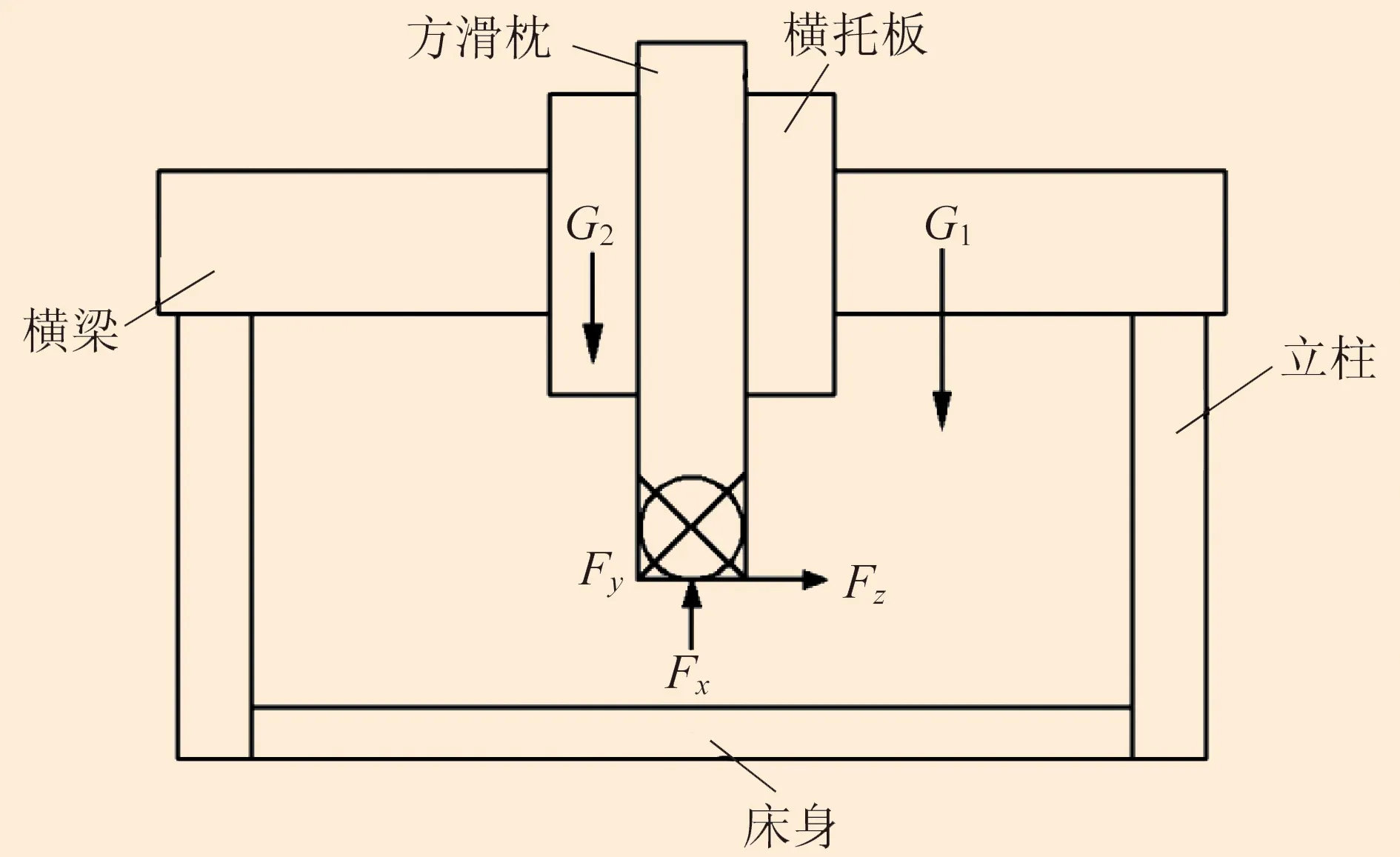
圖4 橫梁結構受力分析

橫梁結構模型約束和載荷如圖5所示。

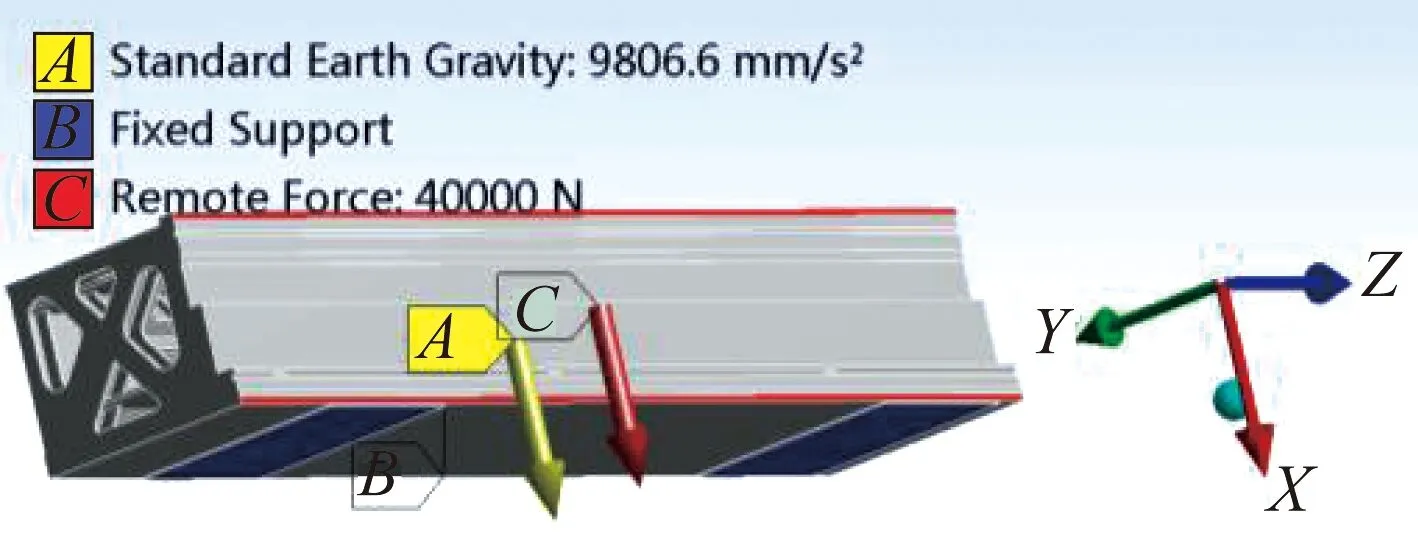
圖5 橫梁結構約束和載荷

3 有限元分析

3.1 變形

經過有限元分析,橫梁結構的整體變形云圖如圖6所示。

圖6 橫梁結構整體變形云圖

在給定載荷下,橫梁結構最大變形量見表2。

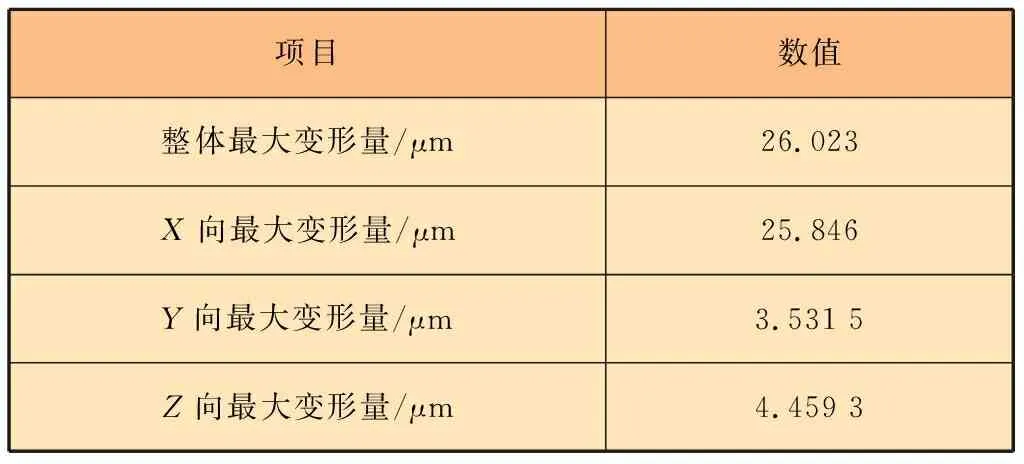
表2 橫梁結構最大變形量

橫梁結構中間部位最大變形量為0.026 mm,兩端位置僅有向上翹起的輕微變形,因此橫梁結構在剛度上有很大富余。可以通過優化橫梁壁厚尺寸,來減小橫梁結構的質量。

3.2 等效應力

橫梁結構整體等效應力云圖如圖7所示。

圖7 橫梁結構整體等效應力云圖

在給定載荷下,橫梁結構最大等效應力見表3。

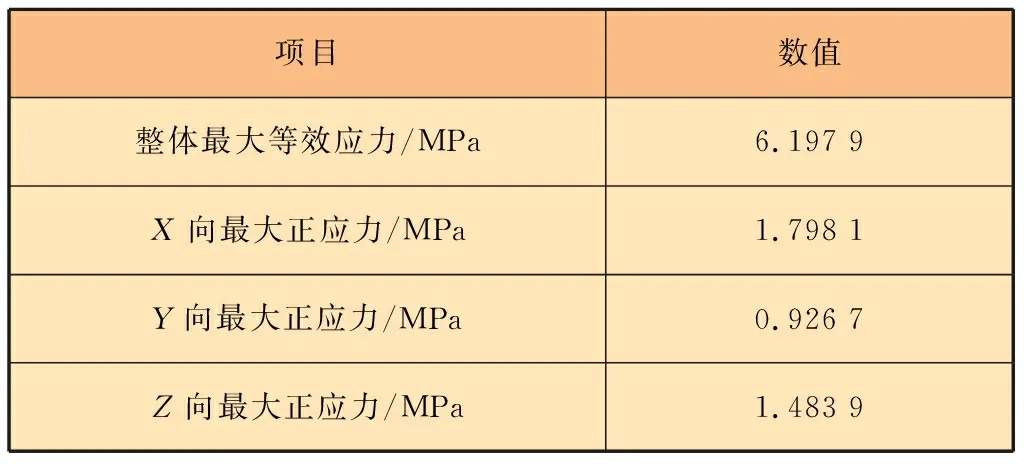
表3 橫梁結構最大等效應力

橫梁結構所受的最大等效應力遠遠小于材料的屈服應力250 MPa,因此并沒有把結構抵抗破環的最大潛能發揮出來,設計過于保守。筆者對橫梁結構進行輕量化設計,使結構的潛能充分發揮出來。

4 動態特性分析

4.1 理論基礎

機床的動態特性可以通過模態分析得到,機床的振動主要由各個零部件的振動疊加而形成。橫梁結構作為龍門銑床的重要部件,其結構對整個機床的加工精度有重要影響[11]。通過模態分析,研究橫梁結構的振動特性,可以確認橫梁結構的固有頻率及振型。

系統的動力學方程為[12]:

(2)

在模態分析中,阻尼可以忽略不計,因此系統的動力學方程為:

(3)

在振動過程中,系統的自由振動為簡諧振動,因此系統的位移函數為正弦函數:

Y=Asin(ωx)

(4)

式中:A為振幅;ω為系統的自振圓頻率。

式(4)代入式(3),可得:

(-ω2[M]+[K]){A}=0

(5)

4.2 模態振型

橫梁結構前兩階模態振型如圖8所示。

橫梁結構前兩階頻率及振型特點見表4。

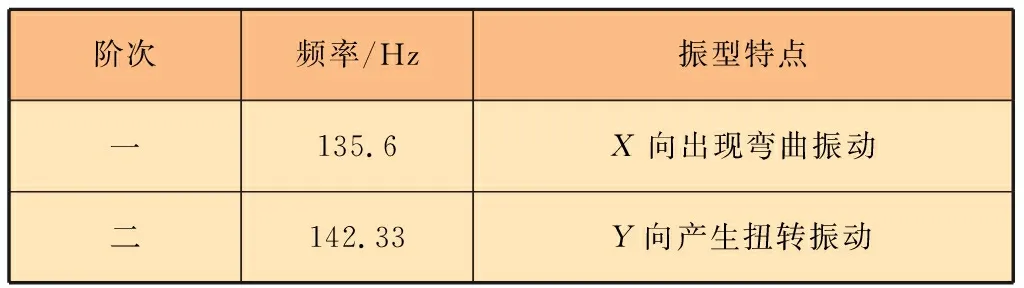
表4 橫梁結構前兩階頻率及振型特點

橫梁結構的一階固有頻率為135.6 Hz。該龍門銑床主軸的最高轉速為6 000 r/min,因此主軸激振頻率的范圍為0～100 Hz[13]。最大激振頻率小于橫梁結構一階固有頻率,即發生共振的概率很小。從振型來看,橫梁結構主要發生彎曲和扭轉振動,說

圖8 橫梁結構模態振型

明橫梁壁厚對橫梁剛度影響較大,故應通過優化尺寸來提高橫梁剛度。

5 輕量化設計

5.1 靈敏度分析

靈敏度分析反映的是目標函數變化對設計變量變化的敏感程度,如果目標函數f可以用一個設計變量x或多個設計變量x1、x2、x3、…、xn來表示,那么靈敏度S可以用目標函數對設計變量的導數或偏導來表示,為[14-15]:

S=df(x)/dx

(6)

S=?f(x1,x2,x3,…,xn)/?xj

j=1,2,3,…,n

(7)

橫梁結構內部較為復雜,尺寸較多,在選取最優設計參數時會存在一定的盲目性。通過靈敏度分析,可以計算出各個設計變量對目標函數的靈敏度值。根據靈敏度值的大小,能夠很快確定出最優的設計參數。

優化中考慮到計算量及計算效率的均衡,選取20個橫梁結構的尺寸作為設計變量。橫梁結構的設計變量如圖9所示,設計變量的取值范圍見表5。

5.2 響應面優化

通過響應面優化,可以直接得到橫梁結構各設計變量的靈敏度值,如圖10所示。

橫梁結構所有設計變量與橫梁結構質量都成正相關,隨著設計變量取值的增大,質量增大。其中,設計變量P16對橫梁結構質量的靈敏度值很小,因此最終的輸入變量剔除設計變量P16。

圖9 橫梁結構設計變量

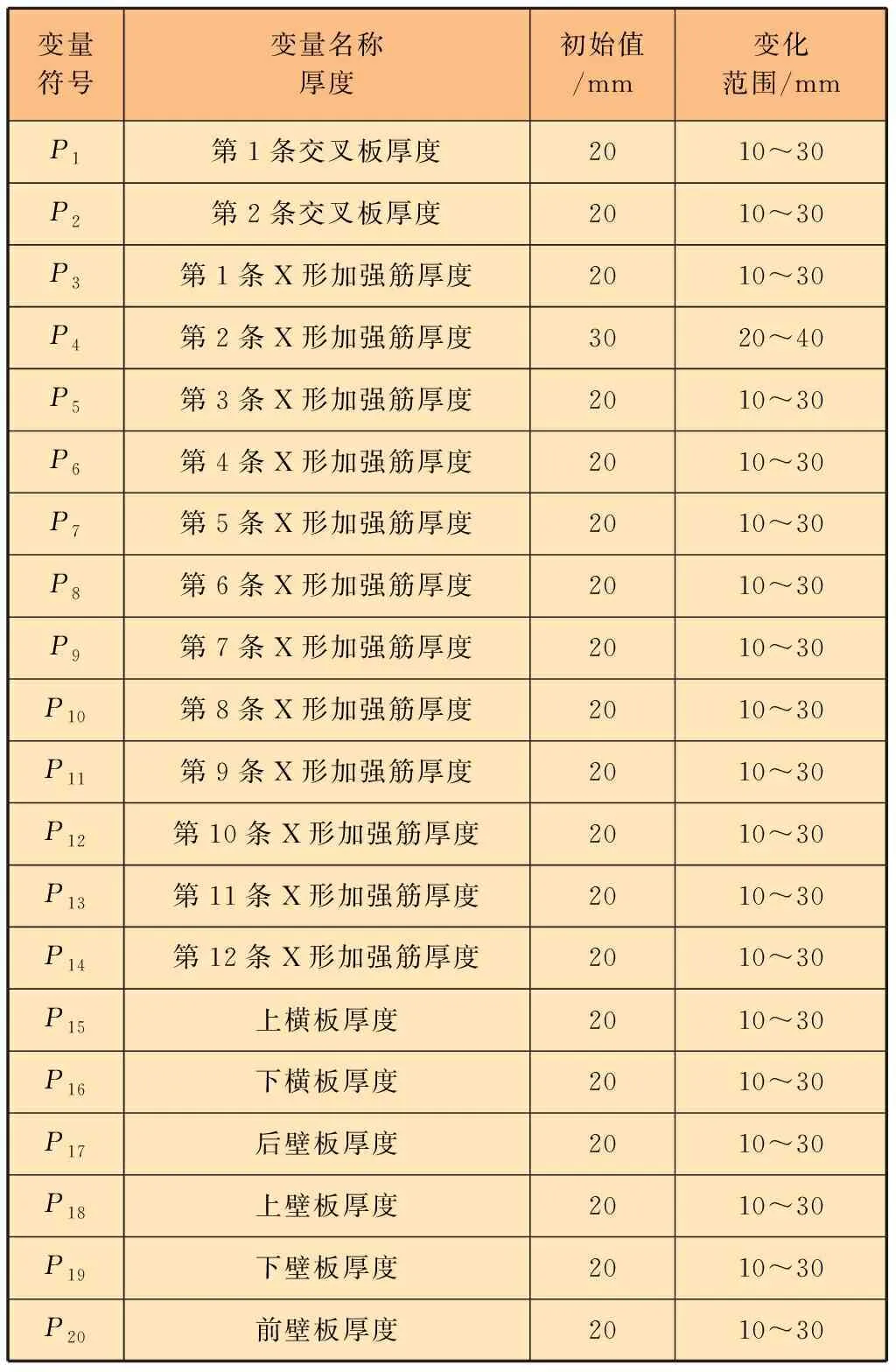
表5 橫梁結構設計變量取值范圍

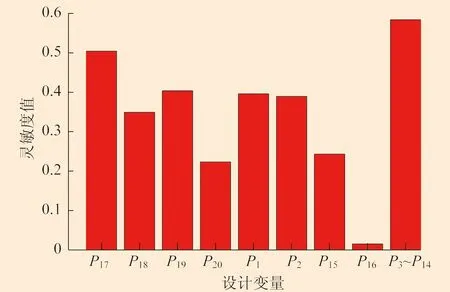
圖10 橫梁結構設計變量靈敏度值

響應面優化指根據試驗設計方法對隨機選取的一組試驗設計變量進行試驗,然后用多元二次方程來擬合各輸入變量與響應之間的函數關系,通過二次多項式來表示響應面模型。響應值G為:

(8)

式中:a0為自由項因數;bi為一次項因數;cii為二次項因數;i代表設計變量。

通過對橫梁結構的有限元分析計算,在保證橫梁結構強度和剛度的前提下,以橫梁結構質量最小為目標,建立響應面優化數學模型[16-17],為:

minfw(X)

(9)

5.3 優化結果分析

通過響應面優化對橫梁進行輕量化設計,得到橫梁結構整體變形云圖、等效應力云圖、前兩階模態振型,依次如圖11、圖12、圖13所示。

輕量化設計前后橫梁結構主要參數的對比見表6。

輕量化設計前,橫梁結構的最大等效應力為6.197 9 MPa。輕量化設計后,最大等效應力減小為5.274 8 MPa,減小了0.923 1 MPa,表明橫梁結構的剛性得到提高。輕量化設計前橫梁結構最大變形量為0.026 mm,輕量化設計后最大變形量為0.025 8 mm,減小了0.000 2 mm,減小百分比為0.77%。輕量化設計前,橫梁結構的質量為10 424 kg。輕量化設計后,橫梁結構的質量為9 341.9 kg,減小了1 082.1 kg,減小百分比為10.38%。輕量化設計前,橫梁結構一階固有頻率為135.6 Hz。輕量化設計后,一階固有頻率為141.41 Hz。一階固有頻率提高了5.81 Hz,提高百分比為4.28%。輕量化設計前,橫梁結構二階固有頻率為142.33 Hz。輕量化設計后,二階固有頻率為148.8 Hz。二階固有頻率提高了6.47 Hz,提高百分比為4.54%。

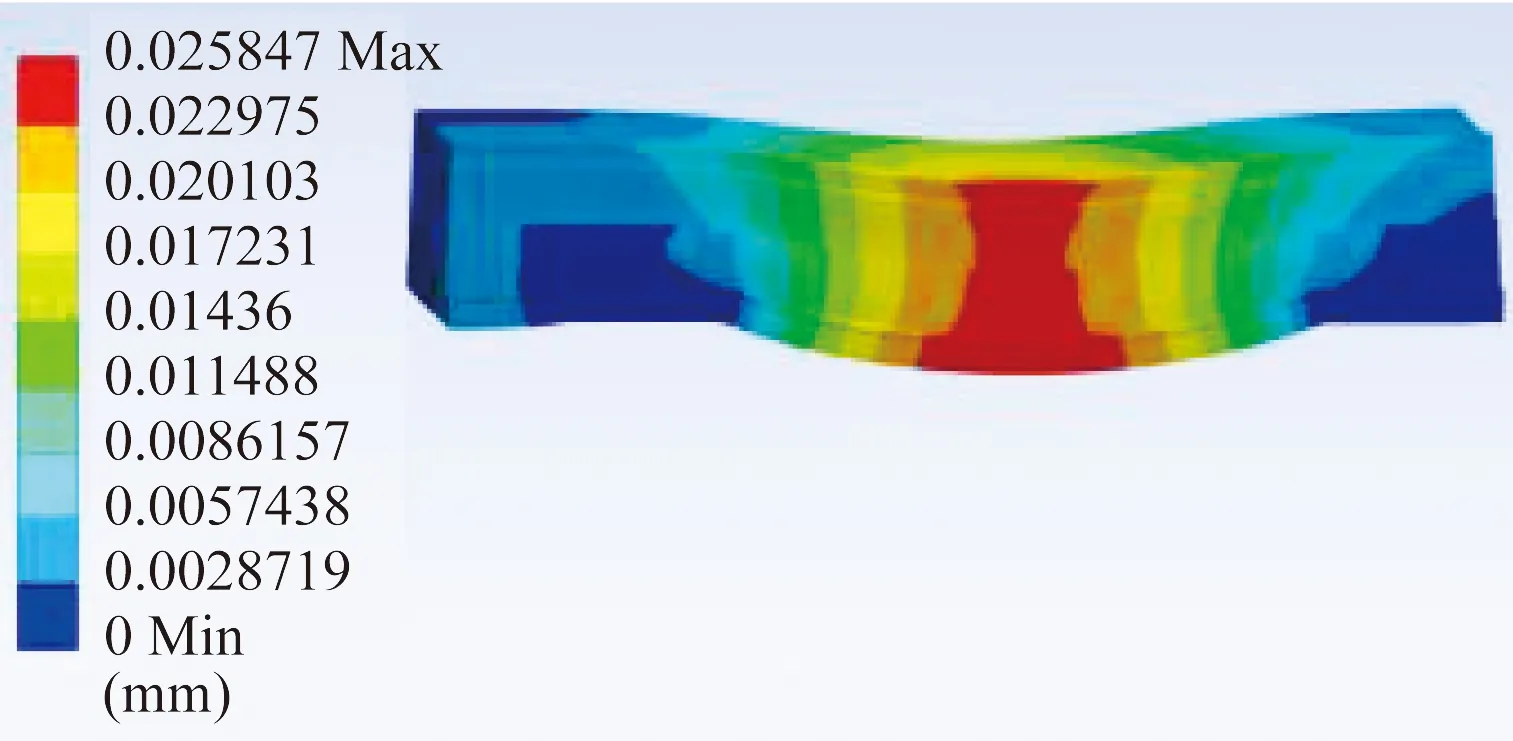
圖11 輕量化設計后橫梁結構整體變形云圖

圖12 輕量化設計后橫梁結構整體等效應力云圖

圖13 輕量化設計后橫梁結構模態振型

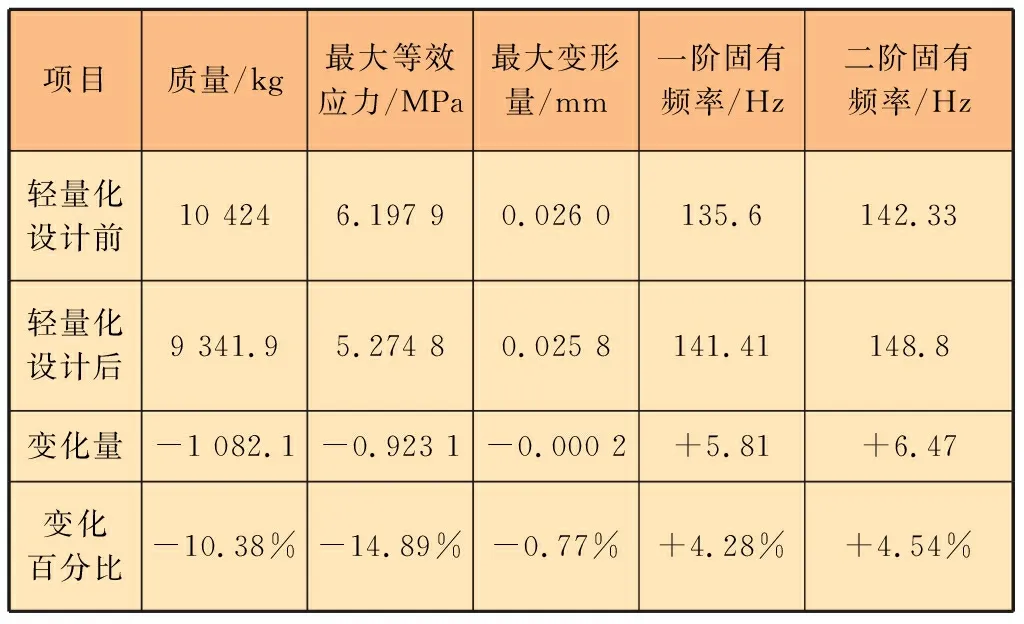
表6 橫梁結構主要參數對比

6 結束語

筆者對龍門銑床橫梁結構進行了輕量化設計。在輕量化設計中,應用靈敏度分析方法,對設計變量進行了篩選,確定了優化參數。通過響應面優化方法,在橫梁結構實體模型的基礎上,以橫梁結構質量最小為目標函數,以橫梁結構等效應力、最大變形,以及一階、二階固有頻率為約束條件,對橫梁結構進行了優化。輕量化設計后的橫梁結構,質量減小了10.38%,一階固有頻率提高了4.28%,二階固有頻率提高了4.54%,在輕量化設計的過程中兼顧了橫梁結構的靜態及動態性能。