遺傳算法與行人疏散模型結合的建筑出口優化

韓雨烔，王維莉，范勤勤，胡志華

上海海事大學 物流研究中心，上海 201306

1 引言

隨著經濟社會的發展，城市化步伐加速推進的同時伴隨著城市人口數量的不斷攀升，許多功能多樣、結構復雜的建筑綜合體應運而生，大規模人群聚集成為當今社會的普遍現象，然而近年來密集人群由于缺乏有效管理、控制而引發的行人踩踏事故頻發，不僅對人民的生命財產造成巨大損失，而且給城市公共安全帶來嚴重威脅。當火災或其他突發事件發生時，建筑或特定區域內的人員需要盡可能快的逃離危險區域，如何確保人員的生命安全以及疏散過程的高效性是公共安全領域的核心目標。因此，對建筑設施進行合理設計、布局，對提高行人疏散的效率、保障人民生命安全具有重大意義。作為建筑疏散的關鍵設施，出口的合理布局尤為關鍵。褚冠全等[1]利用GridFlow 疏散模型研究疏散出口寬度對人員疏散的影響，發現對于較寬的疏散出口條件，當疏散準備時間服從正態分布時，總的疏散時間也服從正態分布。宋衛國等[2]采用社會力模型研究群體疏散過程，不僅重現了實際疏散過程中的典型現象，而且分析了出口寬度、出口厚度等建筑結構特征與疏散時間的關系。Zhao 等[3]通過建立元胞自動機模型模擬出口處疏散的動態過程，得到了有利于疏散的出口寬度及出口間隔，并研究單出口和雙出口對疏散時間的影響，發現建筑空間的疏散出口對稱時各個出口的疏散效率相同，進而可以縮短整體疏散時間。Zhao 等[4]將行人的心理和行為融合到元胞自動機模型，應用于疏散場景，研究認為出口寬度必須大于某個臨界值，出口間隔的最優值與出口寬度無關，但與建筑物的總寬度有關，采用對稱的出口布局更有利于疏散效率的提高。Sticco等[5]運用社會力模型對單室雙出口場景下同側墻兩出口間距與疏散效率的關系進行研究。結果表明兩個出口的間距在一定范圍內不僅不會提高疏散效率，反而會產生“快即是慢”的現象。Alizadeh[6]提出了一種動態的元胞自動機模型來模擬具有障礙物的空間疏散過程，分別考慮了疏散人員的心理，出口位置、寬度及障礙物的位置等基本參數，認為疏散人員的初始分布在獲得的結果中起著重要作用。Tian等[7]通過構建改進的動態場域模型來模擬疏散行人間的交互作用，真實地再現了擁堵過程中前方行人的阻擋效應，同時研究了無障礙房間內出口寬度及位置對疏散時間的影響。Takimoto等[8]研究了行人從單出口大廳疏散的過程，分析了行人在大廳內初始分布位置和最終疏散時間的時空分布關系，并指出二者有很強的關聯性。Cao等[9]提出了一種擴展的多網格模型來研究雙出口房間在火災情境下的疏散問題，對火災發生過程中出口選擇行為展開研究。討論了不同疏散人員類型，效用閾值和疏散準備時間對疏散過程的影響。胡凱等[10]以地鐵站為研究對象，運用仿真軟件從地鐵站出入口數量、樓梯寬度等方面對人群疏散進行模擬研究，通過與設計規范對比發現樓梯的設計是疏散過程的瓶頸。以上研究均將行人在疏散過程中的運動特征進行量化建立了行人運動仿真模型，針對有限出口的布局場景進行動力學分析以及空間疏散能力評估，從而得到較優的出口布局。然而采用基于最優化的方法生成優化的疏散出口布局的研究依然很少。王付宇等[11]從地鐵站人員應急疏散的仿真研究、不同規則下疏散模型的研究和智能算法在疏散建模中的應用三個角度對突發事件下地鐵站人員應急疏散問題進行綜述，提出了把建筑設施因素引入地鐵站人員應急疏散問題中，并利用改進的蟻群算法求解最優疏散路徑。姜立等[12]通過對社會力模型進行修正建立人群疏散仿真模型，同時采用遺傳算法優化障礙物設置，研究發現優化結果不僅有效提高疏散空間內人群的逃生效率而且對建筑設計也有一定啟示。Zhao 等[13]通過在出口前適當放置障礙物來改善恐慌情況下的行人流量，同時采用差分進化算法實現不同形狀障礙物幾何參數的優化，獲得最優疏散效率。研究發現障礙物的所有幾何參數都會顯著影響行人的疏散效率，同時證明相比于柱狀障礙物，板狀障礙物更有助于提高疏散效率。Kurdi等[14]利用模擬退火算法和深度優先搜索技術來優化多個出口的最優分布。通過設計疏散系統研究疏散環境中出口及障礙物的分布對行人疏散效率的影響，并采用多種出口布局進行測試。結果表明，出口的相鄰排布會導致出口前擁堵程度的增加，采用深度優先搜索技術作為疏散策略，會延長疏散時間。Abdelghany等[15]在基于遺傳算法的疏散優化框架中集成元胞自動機仿真模型，解決了多出口的大規模場景下非均勻分布人群的疏散策略問題。

本文構建宏觀-微觀雙層優化框架，在宏觀層通過遺傳算法連續優化生成最有利于疏散的空間布局，在微觀層以行人運動仿真模型模擬該空間布局下人群的疏散動力學過程。與傳統啟發式優化相比，本文提出用疏散仿真結果替代適應度函數，對可行解的評價更加準確，可以得到更加合理的優化結果。該優化框架可以為建筑空間布局設計、應急疏散方案規劃提供理論和方法支持。

2 模型框架

2.1 行人運動仿真模型

本文的行人運動仿真模型基于社會力模型建立[16-17]，該模型以牛頓力學為基礎，引入“社會力”的概念將行人個體運動的內在和外在驅動力分為個體與目標、個體與其他個體、個體與環境的交互。基于牛頓第二定律，質量為mi的行人i期望以速度，朝著目標方向進行疏散，表現為目標驅動力，用表示。在實際疏散過程中假定行人i在時間τi內將實際速度vi調整至，目標驅動力計算公式如（1）所示。同時，行人i在疏散過程中會盡量與其他行人及障礙物保持一定的安全距離，分別用作用力fij和fiw來表示。因此時間t內速度的變化可以用公式（2）所示的動力學方程描述。位置si(t)的改變由速度vi(t)給出。

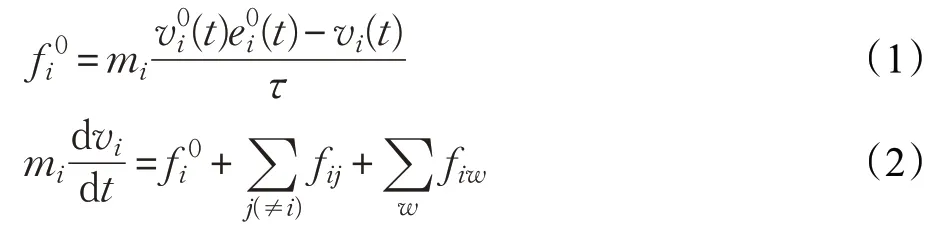
通常行人在運動過程中會與其他行人保持一定的距離，用心理排斥力來表示，其中Ai、Bi為常數；表示行人i和行人j間的距離；rij=(ri+rj)表示行人i和行人j的半徑之和；(si-sj)/dij表示由行人j指向行人i的單位向量；當兩個人的距離小于二者半徑之和時，會因為肢體接觸而產生接觸排斥力，接觸排斥力由兩部分組成，分別為行人間的身體排斥力k(rij-dij)nij和滑動摩擦力κ(rij-dij)Δ，其中k、κ為常數；表示與nij垂直的單位向量；為行人間切線方向的速率差。由此行人間的相互作用力fij可以表示為公式（3）：

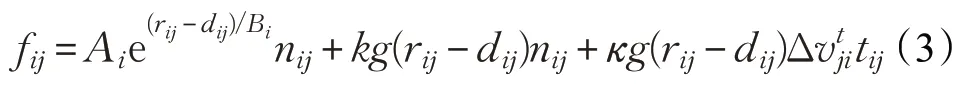
人與障礙物的相互作用力fiw的表達式與fij類似，可表示為公式（4），其中diw表示行人i到障礙物w的距離，niw表示垂直于障礙物的方向，tiw表示與障礙物相切的方向。

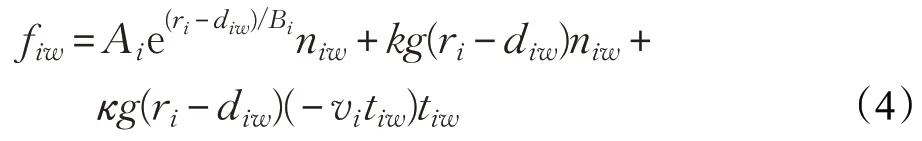
基于文獻[16-17]，本文行人運動仿真模型的參數如表1所示。

表1 社會力模型參數

2.2 基于遺傳算法與行人運動仿真模型的雙層優化框架

疏散出口的布局優化問題具有非線性的特點，本文建立基于遺傳算法與行人運動仿真模型的雙層優化框架，計算獲取最有利于人員疏散的出口布局策略。上層模型利用遺傳算法構建疏散出口布局的優化模型，輸出不同條件下出口位置的備選集合，輸入到下層行人運動仿真模型中，用人群疏散動力學過程的模擬結果替代傳統遺傳算法中的適應度函數，評估不同出口布局染色體下的適應度值，從而引導隨機搜索的方向。其中遺傳算法部分采用實數編碼方式，染色體長度等于決策變量的個數，本文根據空間布局的不同，取出口位置的橫坐標或縱坐標為染色體的組成部分，遺傳算法的參數設置如表2所示。

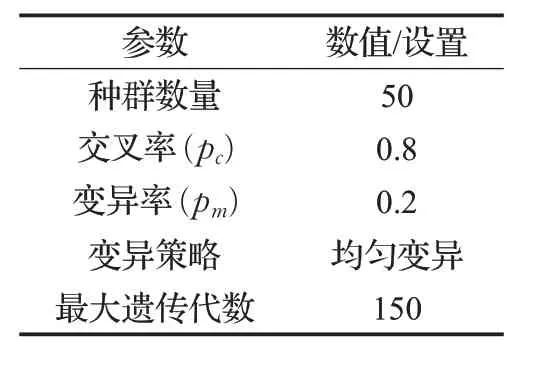
表2 遺傳算法的參數設置

基于遺傳算法與行人運動仿真模型的雙層優化流程如圖1所示。首先隨機生成初始種群，種群中的每個染色體代表一種出口位置布局，接著使用行人運動仿真模型模擬該出口布局下的人群疏散動力學過程，獲取疏散完成時間作為對應染色體的適應度值進行評估。以疏散時間最小化作為遺傳算法迭代優化的方向，根據各個染色體的適應度值，采用輪盤賭的方法進行選擇操作，使優化個體大概率遺傳到下一代；為了對編碼生成的解集空間進行高效搜索，通過交叉和變異操作，將兩個相互配對的染色體以交叉率0.8 交換部分基因，從而形成兩個新的個體；然后采用均勻變異的方法，設置較大的變異率0.2，使種群中染色體的某個基因位發生突變，形成新的個體；繼續對新生成的染色體進行適應度評價；最后重復執行選擇、交叉和變異3種操作，直至發現最優解或到達設定的迭代次數，最終輸出人群的最短疏散時間以及最有利于疏散的出口位置坐標。

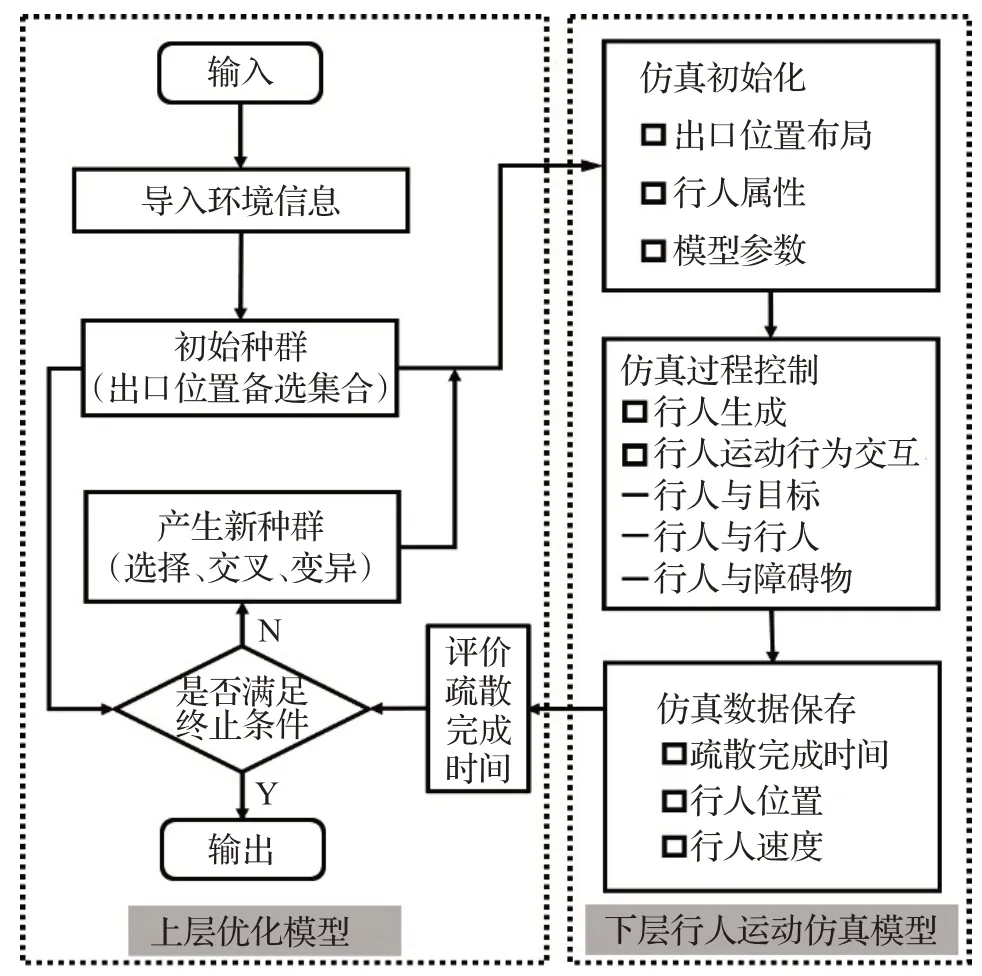
圖1 基于遺傳算法與仿真模型的雙層優化流程圖

3 場景測試及結果討論

3.1 仿真環境

單室是建筑內人員分布的最小單元，其安全出口是在緊急情況下人員疏散的重要通道。根據GB 50016—2014《建筑設計防火規范》的規定，公共建筑內房間疏散門的數量應經計算確定且不少于兩個[18]。因此將仿真環境設置為帶有兩個出口的12 m×12 m的房間，其中兩個出口的寬度分別為DW1和DW2，假定DW1= DW2且取值范圍為0.8～1.6 m。設置3種典型的出口布局：兩個出口設置在同一側，兩個出口設置在相鄰側，兩個出口設置在相對側，如圖2所示。

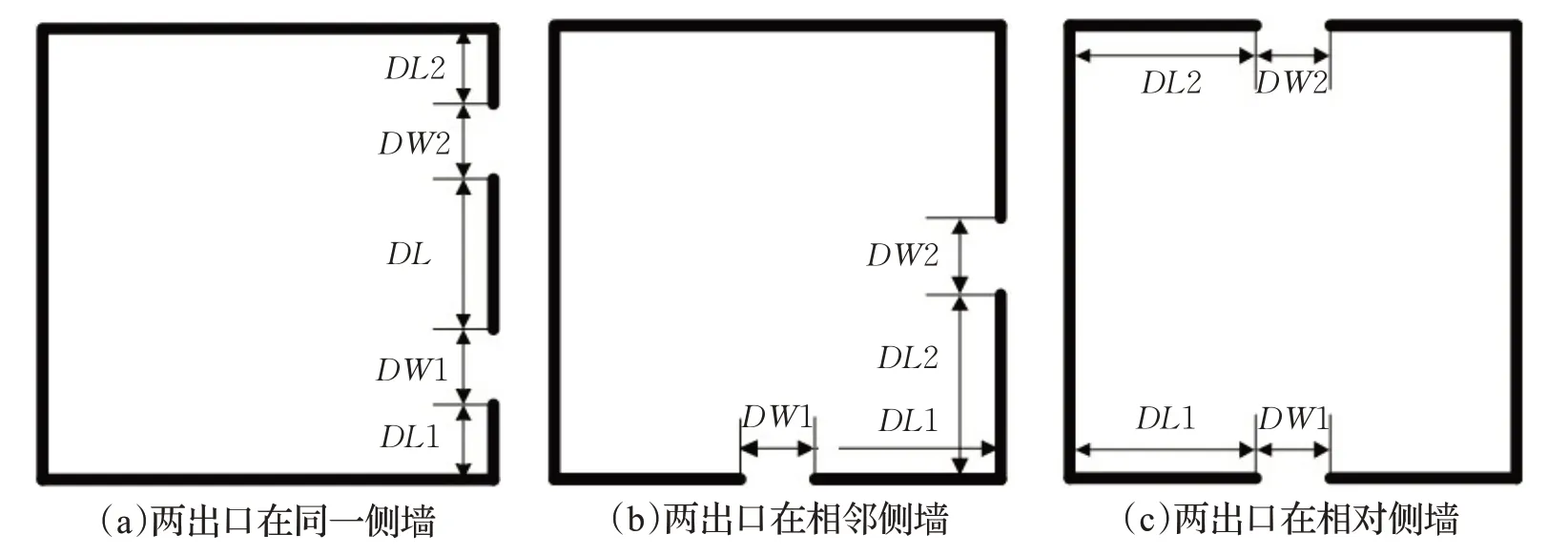
圖2 3種典型的出口布局

人員在房間內的初始分布見圖3（以100 人為例），考慮不同密度情況，安排人員數量分別為49、100、196人（即人員分布密度為0.5人/m2、1人/m2、2人/m2）。假設場景內所有人員同時開始疏散，且均可看見所有出口，并且選擇與個體當前位置距離較近的出口進行疏散。

圖3 人員初始分布圖

3.2 兩個出口在同側的出口位置優化

3.2.1最優出口的位置

基于前述條件，采用遺傳算法對該場景布局下的出口位置進行優化，為了更加直觀地表示優化后兩個出口的空間位置分布，引入變量Δs來表示兩出口之間的距離，在該場景下即為圖2（a）中的DL。不同出口寬度、行人大小以及行人密度下所對應的兩個出口最優位置間的距離，如表3所示。

表3 不同條件下兩出口最優分布間距

根據表3 數據得到圖4，為部分行人半徑和密度下以疏散時間最短為目標獲得的優化的出口位置，圖4（d）表示疏散人群密度相同時，在該場景布局下行人半徑對于最優出口位置的影響。隨著出口寬度的增加，當行人半徑r=0.2 m 時，兩個出口的最優位置逐漸向墻中間靠攏（見圖4（a）），因此人員到出口的距離可能是影響疏散效率的主要原因；當行人半徑r=0.3 m 時，優化的兩個出口位置始終處于同一側墻的兩端（見圖4（b）），在這種情況下即使場景內只有100個人，此時人員在疏散過程也會呈現較擁擠的情況，為避免兩個出口在中間所引發的“羊群效應”，出口分布在墻兩側可能更利于疏散分流從而減少疏散時間。當行人半徑r=0.25 m 時，出口一的優化位置始終在靠近下側墻的一端，出口二的優化位置隨著出口寬度的增加逐漸向中間靠攏（見圖4（c））。

優化疏散結果如表4 所示。為評價出口布局優化結果，本文提出優化率(IP)評價指標，計算公式如式（5）：

其中，TORE為初始布局下人群疏散完成時間，TOPE為優化后人群疏散完成時間。初始布局為遺傳算法生成的初始種群中的最優的出口布局。

3.2.2行人身形尺寸對疏散效率的影響

考慮到性別、年齡以及種族的差異，行人個體的身形差異明顯。本文行人運動仿真模型以圓形表示行人個體，分別取半徑（下述均用r表示）為0.2 m、0.25 m、0.3 m 時，采用遺傳算法對不同身形大小行人條件下的出口位置進行優化。圖5 分別為場景內初始行人分布密度為0.5人/m2和2人/m2時的疏散時間變化，隨著出口寬度的增加，疏散時間整體均呈現下降趨勢；圖5（a）、（b）中的折線均無重疊或交錯情況，并且在出口寬度相同時，隨著行人半徑的增大疏散時間也隨之增加，驗證了行人半徑的增加對于會降低疏散效率；當行人密度為0.5 人/m2時，r=0.2 m 和 0.3 m 時，隨著出口寬度的增加，疏散時間下降明顯，由此可以看出此時出口寬度是影響疏散時間的主要因素；當r=0.2 m，在出口寬度由0.8 m增加到0.9 m時疏散時間下降明顯，然而此后隨著出口寬度的增加，疏散時間基本不變，保持在8.09 s 左右，可以看出在此時出口寬度不再是影響疏散效率的主要因素，因此出口寬度0.9 m 在此情況下為一個臨界寬度。根據上述分析可以得出，疏散出口寬度與疏散效率整體呈正向關系，疏散人員半徑與疏散效率呈負向關系。

圖4 兩出口在同一側的最優位置分布

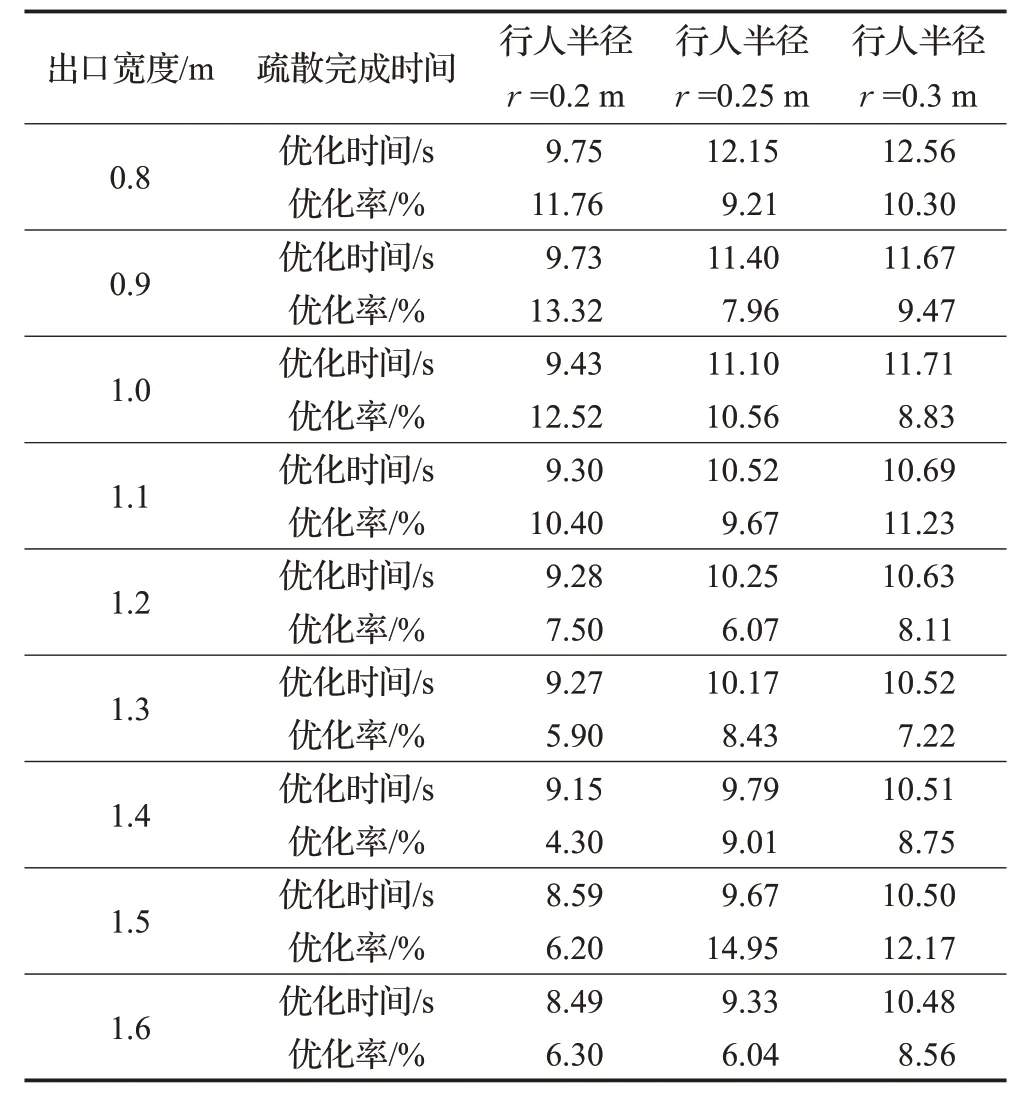
表4 不同疏散條件下的疏散優化結果

3.2.3行人初始密度分布對疏散效率的影響

如圖6 所示，無論r=0.2 m 還是0.3 m ，隨著出口寬度的增加，整體疏散時間大致呈下降趨勢；同時在出口寬度固定的情況下，隨著行人密度的增加，疏散時間增加，對疏散效率具有負向影響。由圖6（a）當r=0.2 m時，出口寬度由0.8 m增加到1.6 m在3種行人密度下疏散時間縮短1 s 左右，出口寬度不再是影響疏散效率的主要因素；由圖6（b）當r=0.3 m 時，行人密度為2人/m2的疏散時間曲線始終與密度為0.5人/m2時差異明顯，即使在出口寬度為1.6 m時，疏散時間依然相差3.44 s。根據以上得出行人初始密度與疏散效率呈負向關系，降低行人密度對于疏散效率的提高影響顯著。

3.3 兩個出口在相鄰側的位置優化

對該出口布局下疏散出口位置進行優化，此時表示兩出口之間距離的變量，見圖 2（b）。行人初始密度為1人/m2情況下，不同出口寬度、行人半徑所對應的兩個出口的最優位置分布，如圖7所示。

其中圖7（a）的縱坐標為Δs，在不同行人半徑下兩個出口的最優位置分別與右邊墻及下邊墻的距離差異不大；圖7（b）～（d）表示不同行人半徑下兩個出口的最優位置在相鄰側的分布情況。當行人半徑r=0.2 m時，隨著出口寬度的增加兩個出口的最優分布相對平穩，大致處于兩側墻中心線偏右的位置。當行人半徑r=0.25 m時，出口寬度為0.8 m時，兩出口的最優位置靠近左邊墻和上邊墻，可以看出在出口寬度最小的情況下該出口分布可實現最大程度的人群分流，從而避免出口前人群擁堵而造成的疏散時間延長；隨著出口寬度的增加，兩個出口的位置均向下邊墻和右邊墻的中心線方向移動，但均分布在中心線偏右位置；當行人半徑r=0.3 m時，兩個出口的分布隨著出口寬度的增加變化幅度較大，當出口寬度小于1 m時兩出口的最優位置為該場景的右下角，當出口寬度大于等于1 m時隨著出口寬度的增加，出口位置由靠近左邊墻和上邊墻下邊墻和右邊墻的中心線方向移動，最終優化的出口布局大致停留在中心線的位置。

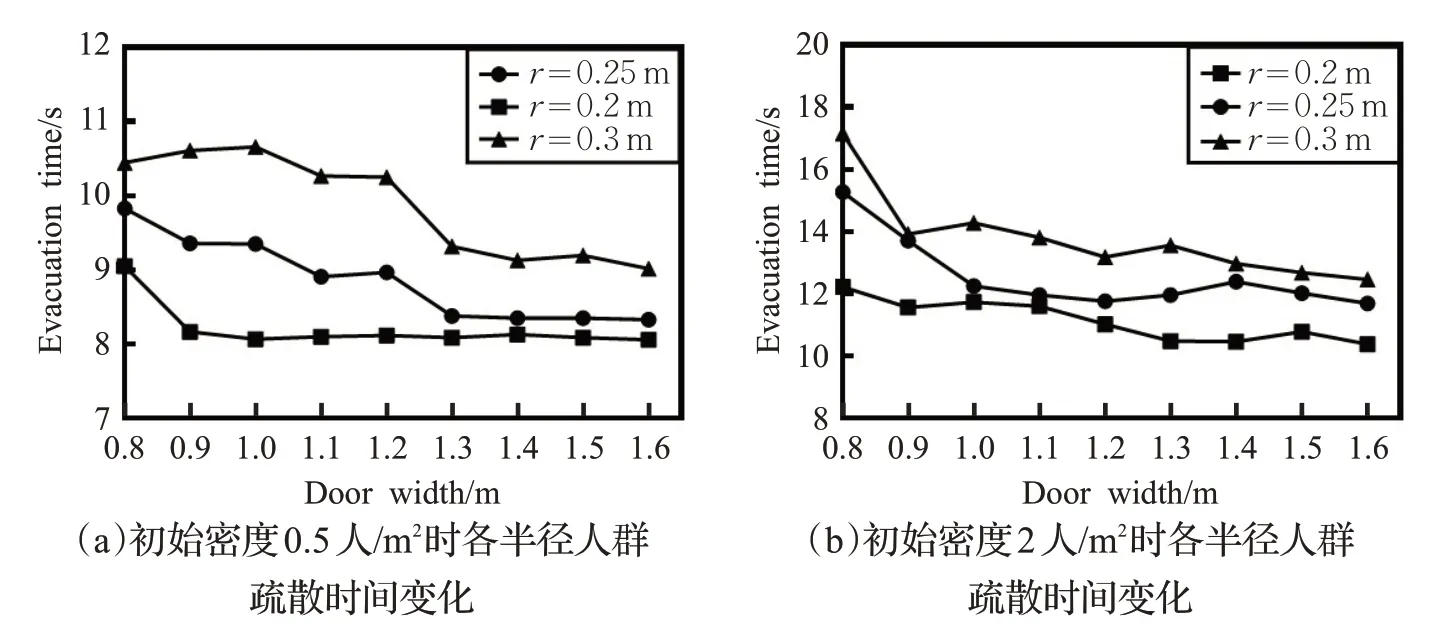
圖5 不同行人初始密度分布下的疏散時間變化

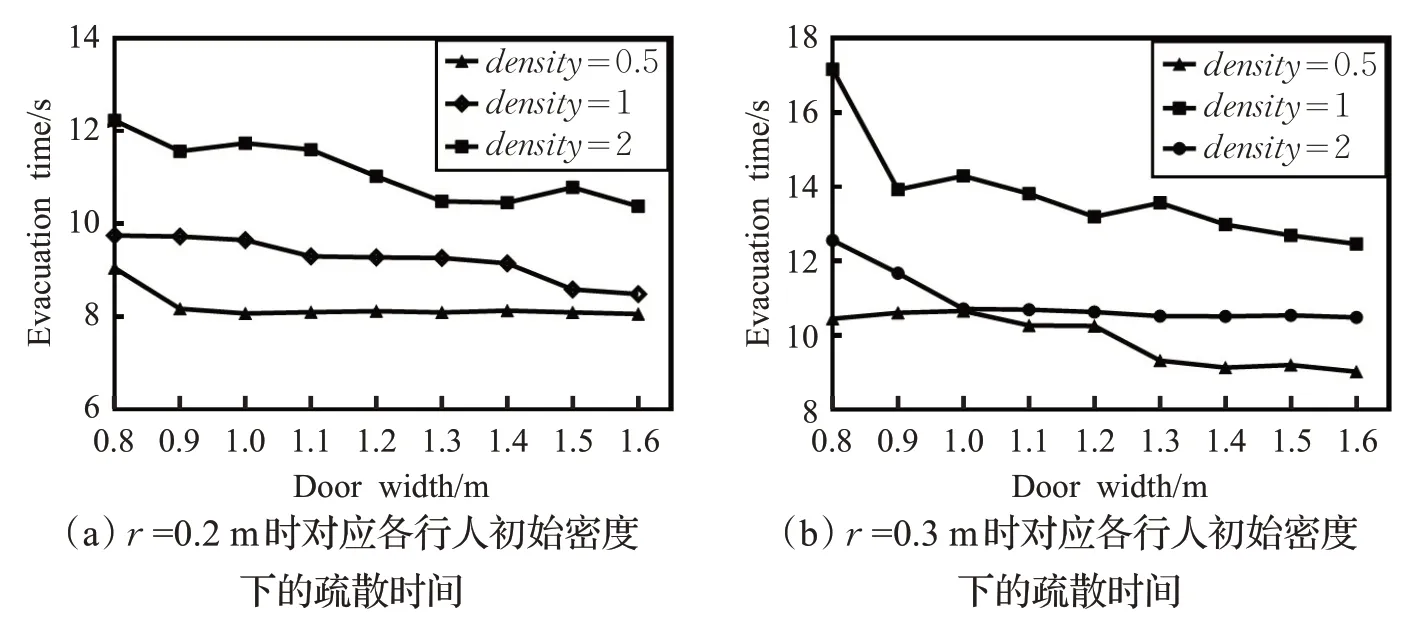
圖6 不同身形半徑人群的疏散時間

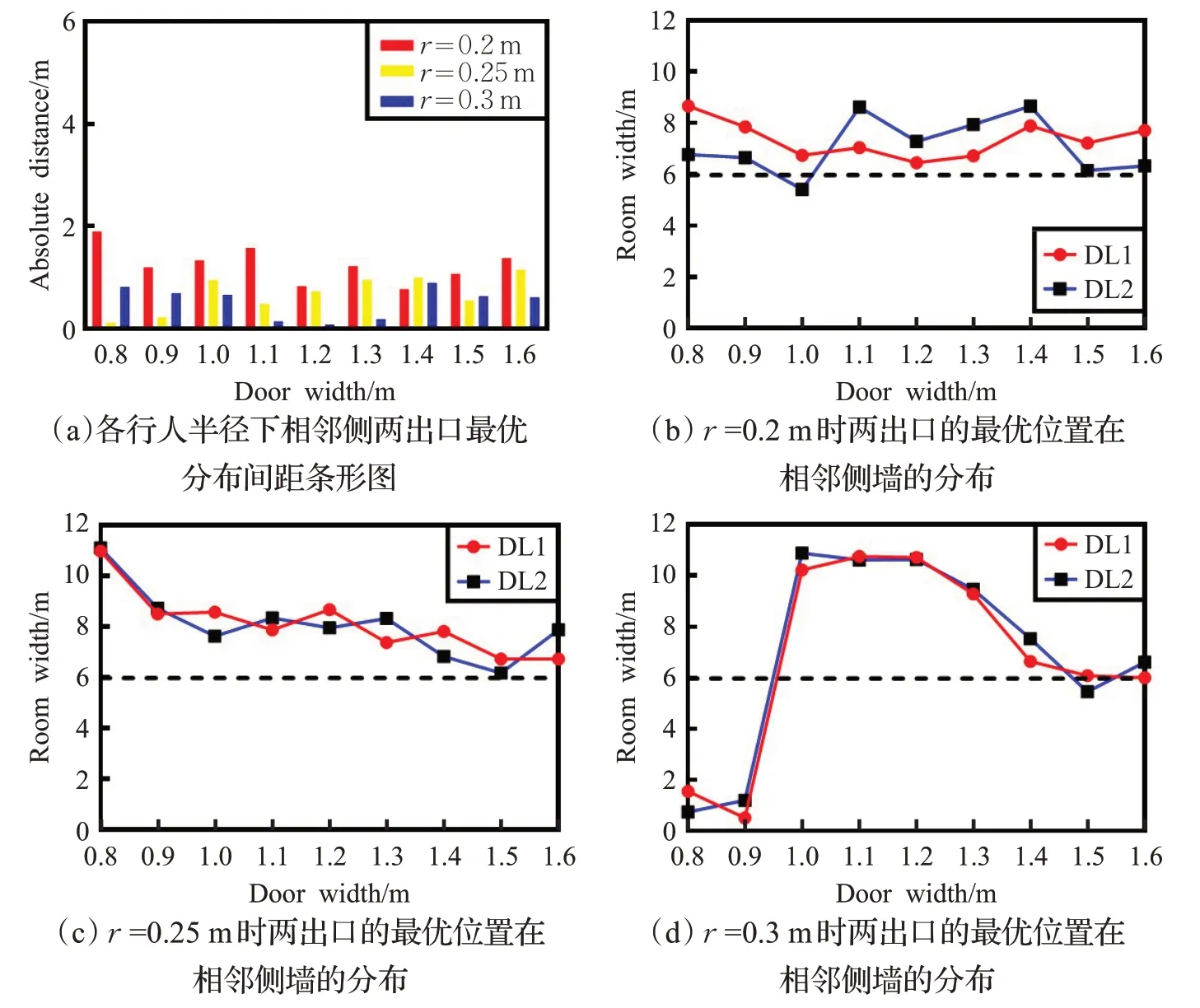
圖7 兩出口分布在相鄰側的最優位置分布

3.4 兩個出口在相對側的位置優化

對該出口布局下疏散出口位置進行優化，兩出口之間的距離的變量，見圖 2（c）。圖 8 為行人初始密度為1人/m2的情況下不同出口寬度、行人半徑所對應的兩個出口的最優位置分布。

與上節場景的分析類似，由圖8（a）得出在不同行人半徑及出口寬度下，出口的最優位置分布的距離相比于上一場景差異更小，因此相對側出口位置的對稱性是影響疏散時間的重要因素。如圖8（b）所示，當行人半徑r=0.2 m時，隨著出口寬度的增加，兩個出口的位置均在接近上邊墻和下邊墻中心線的位置左右平穩波動，此時疏散人員與出口的距離為影響疏散時間的重要因素。如圖8（c）所示，當行人半徑r=0.25 m時，隨著出口寬度的增加，兩個出口的優化位置均由上下邊墻中心線的右側向左接近中心線。如圖8（d）所示，當r=0.3 m 時，在不同出口寬度下，出口的最優位置基本分布在上下墻中心線與右邊墻之間的中間位置。

3.5 出口優化布局場景的疏散效率分析

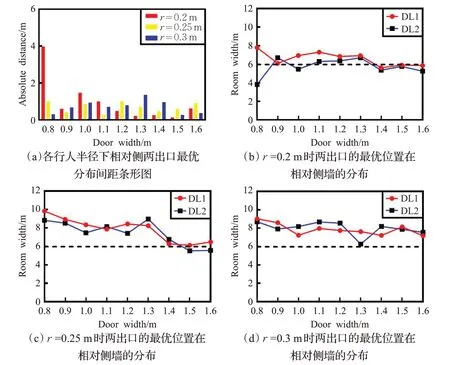
圖8 兩出口分布在相對側的最優位置分布

圖9為不同出口布局下對于3種典型疏散場景的疏散時間的比較情況，圖9（a）的場景中人員半徑最小且人員數量最少，當兩個出口位于同一側時，隨著出口寬度的增加，人群疏散時間在出口寬度為0.9 m 之后幾乎不變，在兩個出口位于相鄰側和相對側的布局中，人群疏散時間一直呈下降趨勢，其中在兩個出口位于相對側布局中的下降趨勢最為明顯，計算得到的最小疏散時間為5.66 s。圖9（b）的場景中人員半徑最大且人員數量最多，當兩個出口位于同一側時，隨著出口寬度的增加，人群疏散時間幾乎沒有變化，而在兩個出口位于相鄰側和相對側的布局中，人群疏散時間呈下降趨勢，且在兩個出口位于相對側布局中的變化趨勢最為明顯，疏散時間由65.09 s 下降至17.19 s，下降幅度為47.9 s。在出口寬度為0.8 m時，3種布局的疏散時間差異最為明顯，分別為65.09 s、41.1 s、17.16 s，并且隨著出口寬度增加，這種差異逐漸縮小。圖9（c）的場景中人員半徑為0.25 m，人員密度為1人/m2，可以看到隨著出口寬度的增加3種布局下的疏散時間均呈下降趨勢，其中在兩個出口位于同一側布局中的下降趨勢最為平緩，疏散時間由12.15 s減少至9.33 s，在兩個出口位于相對側布局的下降趨勢最明顯，疏散時間由22.83 s 減少至9.3 s，并且3 種布局疏散時間差異隨著出口寬度的增加而減少。因此，認為疏散出口的寬度變化對于兩個出口位于相對側的布局的疏散效率影響最大。

圖9 3種出口布局下的疏散時間條形圖

4 結束語

本文在基于遺傳算法的優化模型下集成行人運動模型形成宏觀-微觀雙層優化框架，以疏散時間最短為目標獲得了不同布局下出口的最優位置分布，分別討論了出口寬度、疏散人員半徑、疏散人員密度、出口布局對于人群疏散效率的影響。結果表明：（1）疏散出口寬度與疏散效率呈正向關系；疏散人員半徑、人員密度與疏散效率呈負向關系。（2）疏散場景內行人初始密度為1 人/m2時，隨著出口寬度的增加，不同疏散人員半徑所對應的場景布局中的最優出口分布呈現一定規律性。在兩出口位于相對側的布局中，疏散出口位置的對稱性為影響疏散效率的重要因素。（3）疏散出口的寬度變化對兩出口位于相對側布局的疏散效率影響最大，對兩出口位于同一側布局的疏散效率影響最小。