鋼管混凝土柱恢復力模型研究

朱銘

（江西交通職業技術學院）

0 引言

鋼管混凝土構件是一種新型的組合結構，廣泛應用于房建和大跨度拱橋中[1]。但由于近年來，我國地震頻發，限制了鋼管混凝土在地震區的應用。故研究鋼管混凝土構件在地震作用下的動力響應問題迫在眉睫。

在地震作用下，結構會形成大量的恢復力與變形的關系曲線。如果直接將恢復力曲線用于動力非線性時程分析中，計算過程將十分復雜，故需要將恢復力曲線簡化成恢復力模型來應用。目前，恢復力模型大多是建立在擬靜力試驗的基礎上，根據試驗所得滯回曲線來總結規律，按一定條件加以簡化，最終建立構件的恢復力模型。

本文介紹了目前國內外常見的恢復力模型，并根據文獻[2]中的實測荷載-位移曲線，提出了包含骨架曲線模型、滯回規則、剛度退化的鋼管混凝土柱恢復力模型。

1 恢復力模型分類

目前有兩大類恢復力模型：曲線型模型和折線型模型。曲線形模型是由連續的曲線構成，能很好地表達剛度變化，但是計算方法很復雜，導致其很少應用于實際工程的彈塑性分析。折線型模型則是由折線段構成，模型中存在突變點，不連續，但是計算簡單，故應用廣泛[3]。折線型恢復力模型有雙線型、三線型、四線型、退化雙線型、退化三線型和指向原點型等[4]，適合于不同限制條件下的構件。

1.1 雙線型

雙線型模型的形式簡單，計算方便，并且考慮了鋼材的包辛格效應，可作為鋼筋混凝土構件的彈塑性分析的基礎。但它只有彈性段和強化段，未考慮剛度退化，在結構設計中是偏不安全的。

1.2 三線型

與雙線型相比，三線型考慮了剛度退化的影響，有彈性段、強化段和下降段，可以較好地反映鋼筋混凝土構件的恢復力特性。

1.3 四線型

四線型模型是在三線型的基礎上，引入了構件的開裂點，將開裂點、屈服點、峰值點、極限點作為骨架曲線模型的特征點，更加符合鋼筋混凝土構件帶裂縫工作的特性。

2 恢復力模型建立

本文采用試驗擬合法來建立恢復力模型，現做以下假設：①屈服點與最大彈性荷載點重合；②彈性階段，加載和卸載剛度為構件初始剛度，屈服點后，剛度隨位移增加而退化；③模型中存在軟化點。

2.1 骨架曲線模型

根據文獻[2]的試驗結果，計算兩根圓鋼管混凝土柱的骨架曲線特征點，為了消除不同鋼管柱參數的影響，采用無量綱的形式，最終計算結果見表1。

表1 骨架曲線特征點無量綱值

依據表1 中的各特征點的無量綱坐標，得到骨架曲線的三線型模型，如圖1。各階段方程為：彈性段OA：P/Pm=1.464Δ/Δm，強化段AB：P/Pm=0.426Δ/Δm+0.574，下降段BC：P/Pm=-0.067Δ/Δm+1.067。

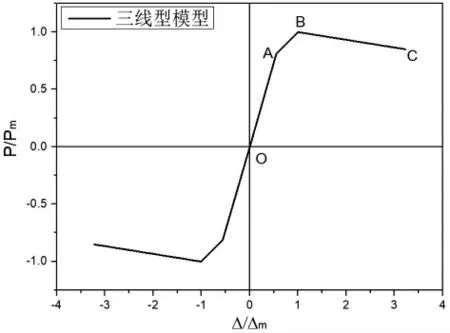
圖1 三線型模型

2.2 剛度退化

隨著循環次數的增大，當加載超過屈服點后，構件不會再以彈性剛度進行卸載，而是有一定的退化。本文按照文獻[5]中的割線剛度來定義構件的剛度。經過對兩根鋼管混凝土柱的剛度進行回歸分析，得到剛度退化的規律如下：

回歸分析過程見圖2。其中，橫坐標為位移循環等級Δi/Δy，縱坐標為各級位移循環的剛度與破壞時的剛度比值Ki/Ku。

圖2 剛度退化回歸曲線

2.3 滯回規則描述

總結實測滯回曲線的規律，再結合骨架曲線模型和剛度退化規律，建立適合鋼管混凝土柱的恢復力模型，如圖3。

圖3 恢復力模型

⑴模型采用無量綱坐標，結合骨架曲線的特征點和各級滯回環建立，圖中A（D）為屈服點，B（E）為峰值點，C（F）為極限點。

⑵在彈性階段，加載曲線沿骨架模型OA 進行，當在OA 段卸載時，沿著原路線返回原點。

⑶構件屈服后，隨著循環次數的增加，卸載剛度降低。當在1 點開始卸載時，先卸載至2 點，接著反向加載至3 點，此時由于模型軟化點的存在，導致在3 點處剛度發生突變，指向4 點。反向卸載至5 點，接著正向加載至6 點，6 點坐標與3 點坐標關于原點對稱，最后回到1點，指向下一個滯回環。軟化點的坐標可參考文獻[6]，取相應位移循環的峰值承載力的0.2 倍。

2.4 恢復力模型與試驗值的比較

將模型和試驗曲線進行比較，如圖4 所示。由圖可知，二者吻合良好，說明本文建立的恢復力模型能較好地反映鋼管混凝土柱的滯回性能。

3 結論

⑴本文在國內外現有的恢復力模型的基礎上，結合試驗滯回曲線，提出了適合鋼管混凝土柱的恢復力模型，并且與擬靜力試驗得到的滯回曲線對比。通過模型建立的恢復力曲線與試驗曲線比較相符，證明推導的恢復力模型是合理的。

⑵由于參考的試驗滯回曲線較少，未能充分反映影響鋼管混凝土柱滯回性能的各因素，故還需更加深入、全面的研究，方能得到更加實用的恢復力模型。

圖4 恢復力模型曲線與試驗曲線對比