基于均勻同心圓陣列的近場寬帶波束形成

孟子健，王沛曌，陳海華，2

1.南開大學 電子信息與光學工程學院，天津 300350；2.天津市光電傳感器與傳感網絡技術重點實驗室，天津 300350)

0 引言

自適應波束形成技術通過改變波束形成權重系數來抑制干擾信號并提高期望信號的接收增益。近年來，隨著移動通信的發展和數字信號處理技術的廣泛應用，自適應波束形成技術除了在雷達、聲納、空間濾波和定位等領域發揮重要作用外，同時也在麥克風陣列語音處理、無線通信等方向有了長足發展[1]。

傳統波束形成法一般假設信號源與陣列中心的距離遠大于陣列尺寸，即滿足信號處于陣列遠場的假設，因而可用平面波來近似到達信號[2]。在雷達和無線通信等應用系統中，上述假設較合理，其近似誤差較小。然而，在許多其他場合中，如麥克風陣列語音處理、醫學成像等領域，信號源與陣列的距離通常較短。在這種情況下，把到達陣列的信號近似為平面波所帶來的誤差較大，這將使波束形成的性能急劇降低。因此，國內外學者提出了多種近場波束形成方法，如用時延來彌補傳感器之間的信號延遲差異，或通過近似曲率來彌補近場誤差。文獻[3]提出了一種可使波束聚焦于任意徑向距離的方法，極大地擴展了傳統波束形成方法的應用范圍。

此外，設計寬帶信號的波束形成還存在一個問題，即陣列響應會隨著頻率的變化而變化。在近場寬帶陣列中，情形更復雜。在某些情況下，陣列響應在信號的高頻段呈現遠場信號的特點，而在信號的低頻段則呈現近場信號的特點[4]。傳統寬帶陣列信號處理采用帶自適應系數的抽頭延遲線(TDL)濾波器，TDL抽頭個數與信號帶寬成正比，因而其計算復雜度和硬件復雜度隨著帶寬的增加而急劇升高[5]。相較于TDL法，子帶分解技術、部分自適應波束形成法和頻率響應不變波束形成器(FIB)[6]等方法的計算復雜度均有降低。傳統的FIB法以均勻線性陣列為基礎，由于均勻圓陣(UCA)的空間對稱性，基于其設計的FIB具有電子可旋轉特性，即波束形成的聚焦方向可通過改變陣列權重來旋轉。此外，基于其對稱特性，UCA-FIB的頻率補償網絡與波束形成權重可以分開設計，故可預先離線設計以補償網絡，僅剩波束形成權重系數由自適應算法在線設計。因此，與其他寬帶Beamforming算法相比,UCA-FIB在線運算復雜度較低[7]。在此基礎上改進得到的均勻同心圓陣列(UCCA)FIB可緩解UCA-FIB中帶寬受限的問題[8]。

本文提出了一種新的頻率不變近場寬帶波束形成的方法。該方法采用UCCA，借助多個陣列圓環間的相互補償作用，可在更寬的頻帶上實現頻率響應不變的近場寬帶波束形成。該方法首先將同一個陣列環上各天線接收到的信號轉化為相位模式，再將多個陣列環上對應的相位模式信號疊加。每路疊加后的相位模式信號通過近場矯正因子和頻率補償網絡進行補償，以消除近場效應和寬帶信號的頻率依賴性，最后使用波束形成權向量系數對所有相位模式信號進行加權求和,得到陣列的輸出信號。鑒于UCCA的對稱性，近場修正系數和頻率補償網絡與波束形成權重向量可分開設計，因而前兩者可預先離線完成，而波束形成系數可根據信號到達角進行自適應調整，極大地降低了系統的計算復雜度。仿真結果表明，該方法能夠獲得理想的具有頻率不變特性的波束圖。與其他自適應波束形成法相比，UCCA-FIB可大幅提高波束形成的性能。

1 近場UCCA-FIB原理

圖1 UCCA結構圖

現假設信號與陣列處于同一平面，則第(k,p)個傳感器的輸出信號為

(1)

式中：f為信號的頻率；φ為近場寬帶信號s(t)的方位角；ρ為信源與陣列中心的距離；S(f)為s(t)的頻率響應；c為信號波的傳輸速度。

(2)

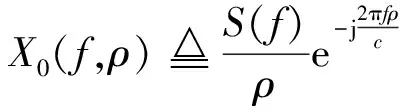
(3)

每個圓環上的輸出信號經離散傅里葉逆變換(IDFT)轉換成相位模式信號，第p個圓環上的第m路相位模式信號為

(4)

式中m=-M,-M+1,…,M，M=(L-1)/2，L≤K是每個環上的相位模式總數，本文取L為奇數。L為偶數時與文中方法類似。

為了修正近場畸變，本文在每個相位模式信號上采用一個矯正系數gm,p對其進行矯正。如圖2所示，各圓環上經矯正后具有相同階數m的相位模式信號相加后，通過頻率補償網絡Hm(ω)來消除寬帶陣列響應的頻率依賴性。最后，經過近場矯正和頻率響應補償的信號乘上波束形成權系數wm并求和，即可得到波束形成器的輸出信號。綜上，波束形成器輸出的頻率響應為

(5)

圖2 FIB原理圖

將式(3)、(4)代入式(5)，得到陣列輸出為

(6)

(7)

式(7)可近似為

(8)

由式(8)可看出，通過選擇合適的gm,p和Hm(ω)，可使

(9)

則式(8)可等價為

(10)

由式(10)可知，本文設計的UCCA時空響應可達到近似頻率不變。此外，該陣列的波束圖僅由波束形成加權系數wm決定。因此，該陣列中的補償網絡可以離線設計，而波束模式可進行自適應調整，故算法復雜度大幅降低。

gm,p和Hm(ω)可通過凸優化理論設計。假設補償濾波器在頻率ω0處有Hm(ω0)=1。此時，由式(8)可知，設計近場矯正系數即是找到gm,p，使

(11)

其中：

(12)

頻率補償網絡主要由一個長度為LF的濾波器組成。第m個相位模式濾波器的沖激響應記為hm?[hm1,hm2,…,hmLF-1]，則濾波器的頻率響應為

(13)

式中ei?[1,e-jωi,…,e-j(LF-1)ωi]T。頻率補償網絡的設計思路就是找到hm滿足：

(14)

其中:

(15)

式中：ωi∈(ωL,ωU)；Nω為頻率取樣個數。

式(11)、(14)均可以轉換成二階錐規劃(SOCP)問題，因而可以通過凸優化工具快速地求解[10]。

2 近場UCCA-FIB的自適應波束形成

利用第1節提出的近場UCCA-FIB，本節研究其自適應波束形成方法，即wm的設計。假設期望信號S(ω)以方位角φs到達陣列，同時有干擾信號I(ω)以方位角φI到達陣列，利用式(1)，陣列第p個圓環上的輸出可寫成

(16)

(17)

(18)

(19)

由式(19)可知，本文提出的近場UCCA-FIB的輸出相當于一個遠場均勻線性陣列。因此，傳統的自適應波束形成算法可以推廣到該陣列中。根據式(19)，對每路相位模式信號進行波束形成加權并求和，則可得到波束形成的輸出信號

(20)

式中w?[w-M,w-M+1,…,wM]T為波束形成權重向量。該向量可通過最優化輸出信號的信干噪比(SINR)得到，其優化模型為

(21)

(22)

在實際計算過程中，一般使用樣本協方差矩陣代替干擾噪聲協方差矩陣計算，即

(23)

3 仿真結果

為了驗證本文提出的近場寬帶陣列的性能，本節設計了一個UCCA-FIB以及基于此而設計的SMI波束形成方法。在本文的設計例子中，陣列由兩個圓環組成，即P=2，每個圓環上有12個天線或傳感器，即K=12。相位模式的個數L=9，研究的頻段為ω∈[0.35π,0.5π]，ρ=20λ。在第一個例子中，考察UCCA-FIB的頻率響應不變特性和近場矯正效果，為簡單起見，取波束形成權向量為w=[1,1,…,1]T。根據第1節中的設計方法得到近場矯正系數和頻率補償網絡，陣列的波束圖如圖3所示。由圖可看出，本文提出的寬帶近場UCCA-FIB在目標頻段近似頻率不變。

圖3 近場FI-UCCA的波束方向圖與ω的關系

圖4為有無近場矯正時的波束圖。由圖可見，經近場矯正后的陣列響應具有更低的旁瓣，實現了近場矯正。

圖4 有無近場矯正的波束圖對比

在本文第二個例子中，使用第一個例子中設計的近場UCCA-FIB來評估波束形成的性能。設期望寬帶信號以φs=0°到達陣列，與同心圓陣中心的距離ρs=20λ。同時假設干擾信號的入場方位角φI=80°，與同心圓陣中心的距離ρI=25λ。假設輸入信噪比為0，干噪比(INR)為20 dB。使用近場UCCA-FIB進行波束形成的輸出SINR隨著輸入信噪比(SNR)的變化情況如圖5所示。同時，圖5還給出了無近場矯正UCCA-FIB和TDL的波束形成性能。由圖可見，使用近場UCCA-FIB進行波束形成后，與其他兩種方法相比，輸出SINR有明顯改善。

圖5 波束形成性能比較

4 結束語

本文介紹了一種均勻同心圓陣頻率響應不變的近場寬帶波束形成器設計方法。該方法利用近場矯正系數修正了近場效應，采用頻率補償網絡消除了陣列響應的頻率依賴性，將近場寬帶陣列的波束形成問題轉化為遠場窄帶陣列波束形成問題。因此，絕大部分傳統窄帶波束形成方法可以應用到本文提出的近場寬帶陣列中。仿真結果表明，本文提出的近場同心圓陣列算法可行，做到了頻率響應不變的要求。與其他近場寬帶波束形成方法相比，同心圓陣列在波束形成方面具有更好的性能。