大型PCTC船車輛跳板端部鉸鏈動載荷分析

黃 辰，余 龍

（1. 上海德瑞斯華海船用設備有限公司，上海 200093；2. 上海交通大學 海洋工程國家重點實驗室，上海 200240）

0 引 言

作為大型滾裝船的重要組成部分，滾裝通道設備對于實現滾裝船的運輸和裝卸功能而言具有重要的作用。在通道設備中，車輛跳板是連接船舶與碼頭的橋梁，是車輛進出船舶的主要通道。在裝卸車輛時，車輛跳板主要依靠與船體鉸接的多組鉸鏈來傳遞其受到的各種作用力，包括跳板自重、車輛載荷和船舶與碼頭相對運動產生的摩擦力。因此，對端部鉸鏈進行強度校核是車輛跳板設計中十分重要的環節，直接關系到車輛跳板的安全性。在對鉸鏈進行強度校核時，計算鉸鏈受到的作用力是十分關鍵的，該作用力與車輛載荷有直接的關系。在對鉸鏈進行強度規范校核時，處理車輛載荷采取的方法通常是用車輛軸載荷乘以1.1倍動載荷系數，將其轉化為靜載荷之后采用估算法或有限元軟件進行計算，最終得到鉸鏈的應力[1]。針對車輛跳板結構強度的相關理論和試驗研究大多是基于該思想開展的[2-4]。

車輛行駛時產生的載荷往往與車速和路面平整度有很大關系[5]。一般情況下，滾裝通道設備設計廠家會對車輛（尤其是大型車輛）通過跳板的速度有一定的要求。然而，在實際運營過程中，為提高裝卸效率，車輛通過跳板的速度往往難以滿足滾裝通道設備設計廠家的要求。另外，大型滾裝船車輛跳板均為多節設計，跳板節與節之間的過渡區域和跳板表面的防滑設計都可能造成車輛載荷的實際值比船級社規范規定的數值大，導致結構趨于危險。

本文提出大型滾裝船跳板的動載荷計算方法，并以某巴拿馬級PCTC（Pure Car and Truck Carrier）車輛艉跳板為分析對象，對其承載車輛運行的動態過程進行動力學仿真，計算得到鉸鏈受力的動態載荷譜。相比于將車輛載荷轉化為靜載荷的處理方法，動力學仿真計算便于對鉸鏈在不同車型、不同車速條件下的受力情況進行分析，并能更真實地反映出車輛載荷的實際作用情況。

1 理論基礎

多體系統的動力學分析是根據牛頓定理給出自由物體的變分運動方程，并運用拉格朗日乘子定理推導出基于約束的多體系統動力學方程。MSC·ADAMS是由美國MDI公司開發的虛擬樣機分析軟件，依據上述方法，ADAMS可自動建立系統的動力學微分-代數方程[6]，即

式(1)中：q為系統廣義坐標列陣；u為系統廣義速度列陣；P為系統動量；T為系統動能；φ為系統約束方程；λ為拉氏乘子列陣；F為系統廣義力列陣；t為時間。為求解上述方程，ADAMS可根據機械系統特性，選擇不同的數值積分算法。對于剛性系統，ADAMS采用變系數的向后微分公式（Backwards Differentiation Formulation, BDF）剛性積分程序求解，這是自動變階、變步長的預估矯正法，分別以Index3、SI2和SI1積分格式，在積分的每一步采用修正的 Newton-Raphson迭代算法迅速、準確地求解，從而得到用戶所需的各種動力學計算結果。

2 動載荷計算流程

本文采用MSC·ADAMS建立仿真模型，主要包括跳板-車輛實體模型、約束邊界條件的添加和接觸力的定義等3部分。完成上述3部分工作之后，即可使用ADAMS中的仿真模塊對車輛通過跳板的過程進行動力學仿真，并得到鉸鏈受力的時歷譜。另外，采用有限元分析軟件MSC·PATRAN/NASTRAN 建 立 跳板的FEM（Finite Element Method）模型，并根據規范要求得到靜力條件下鉸鏈的受力。最后，根據上述計算結果，對采用動力學方法和靜力學方法得到的計算結果進行對比分析。鉸鏈動載荷計算流程見圖1。

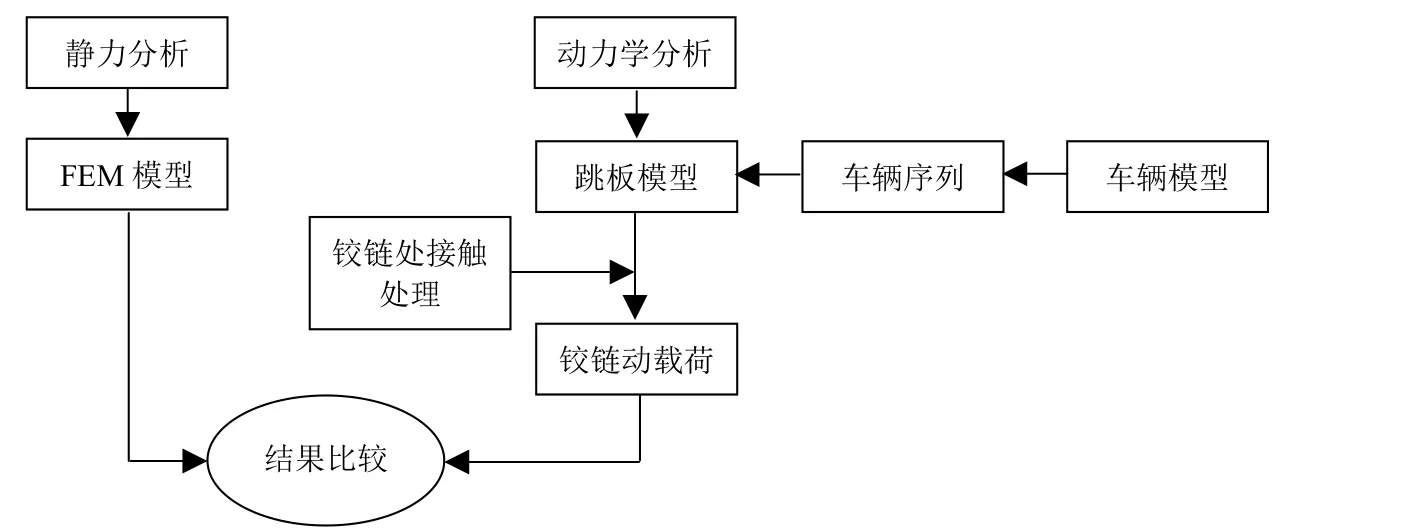
圖1 鉸鏈動載荷計算流程

3 算例分析

3.1 靜力分析

計算所用PCTC的跳板總長40m，車道寬5.9m，共由3節組成，總重約180t。跳板與船體中心線的夾角為 34°，完全開啟用時約15min。轎車、卡車、客車和拖車等不同種類的車輛均可在該跳板上通行，其中重載車輛的載荷達150t。采用有限元分析軟件MSC·PATRAN/NASTRAN對該跳板進行建模計算，得到端部鉸鏈在滿足規范要求的車輛載荷作用下的受力值。

3.1.1 有限元建模

由于車輛跳板大部分為板和梁組成的框架結構，因此采用自動化分網格的方法生成四邊形單元（Quad4），整個模型共有9183個單元。為方便討論，按從左舷到右舷的順序將主鉸鏈命名為主鉸鏈A和主鉸鏈B，將副鉸鏈命名為副鉸鏈1～副鉸鏈4。車輛跳板結構見圖2，車輛跳板有限元模型見圖3。車輛跳板所用鋼板為船用高強度鋼，材料的物理屬性定義為：彈性模量E=2.06×1011GPa；泊松比0.3；剪切模量G=0.792×1011GPa；屈服強度355MPa。對于跳板頂板、縱桁腹板、橫梁腹板、面板和鉸鏈眼板等直接由鋼板構成的結構，其單元類型定義為2D板殼單元（shell）；對于頂板上2個縱桁間的扶強材，其單元類型定義為1D梁單元（beam），梁單元截面特性根據實際設計定義。

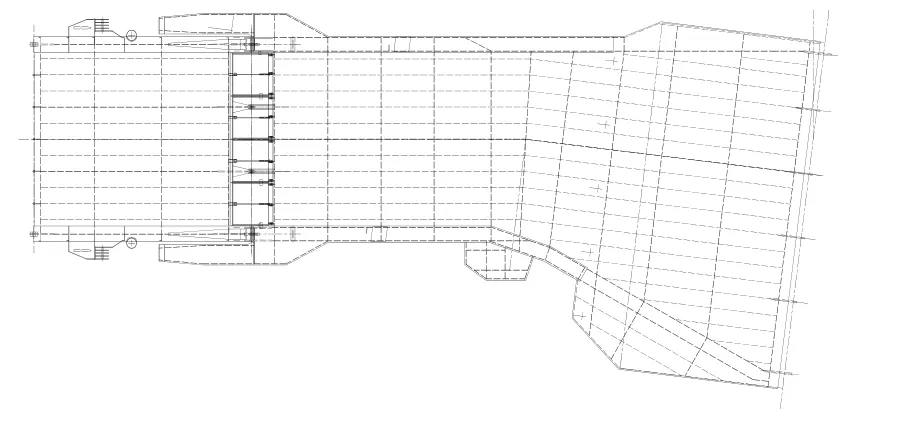
圖2 車輛跳板結構

圖3 車輛跳板有限元模型

3.1.2 邊界約束條件

車輛跳板打開之后，一端依靠鉸鏈與船體鉸接，另一端搭接在碼頭上，2節跳板之間依靠中間鉸鏈與調節油缸連接并保持2節之間變形一致。因此，跳板模型的邊界條件主要包括端部鉸鏈與船體之間的約束、2節跳板之間鉸鏈的約束和第二節跳板與碼頭之間的約束等3方面。

在設計時，車輛跳板最外側2個主鉸鏈沿x方向（船長方向）和z方向（垂直方向）的平移被約束為0；副鉸鏈眼板與鉸鏈軸之間留有2mm的間隙，因此沿x方向（船長方向）的平移被約束為0，沿z方向（垂直方向）的平移可移動2mm；第二節跳板搭接在碼頭上時，僅z方向的平移被約束為0。在中間鉸鏈處，2節跳板在x方向和z方向上的變形是完全相同的；在調節油缸處，2節跳板在x方向上的相對變形是完全相同的。因此，在中間鉸鏈和調節油缸處，需添加多點約束（Multi-Point Constrain, MPC），以保證第一節跳板和第二節跳板在這些節點變形的一致性。

車輛跳板PATRAN模型的邊界約束條件見表1。

表1 車輛跳板PATRAN模型的邊界約束條件

3.1.3 計算載荷和工況

車輛跳板受到自身重力和車輛載荷的作用，其中重力可由PATRAN模型自動添加計算。通過跳板的重型自卸車軸的載荷為30t，車輛總重達150t，其載荷通過5根車軸（共10組車輪）作用在跳板上。在計算時，根據車輛軸距和輪距共添加10個z方向的作用力，按規范考慮1.1倍動載荷系數，則每個作用力的大小為165000N。為全面考察各組鉸鏈的受力情況，分別計算以下2種工況：

a) 工況一，車輛沿跳板中間區域通過并作用在跳板鉸鏈一端；

b) 工況二，車輛沿主鉸鏈A一側通過并作用在跳板鉸鏈一端。

計算得到的2種工況下各組鉸鏈的受力見圖4和圖5，端部各組鉸鏈受力值見表2。

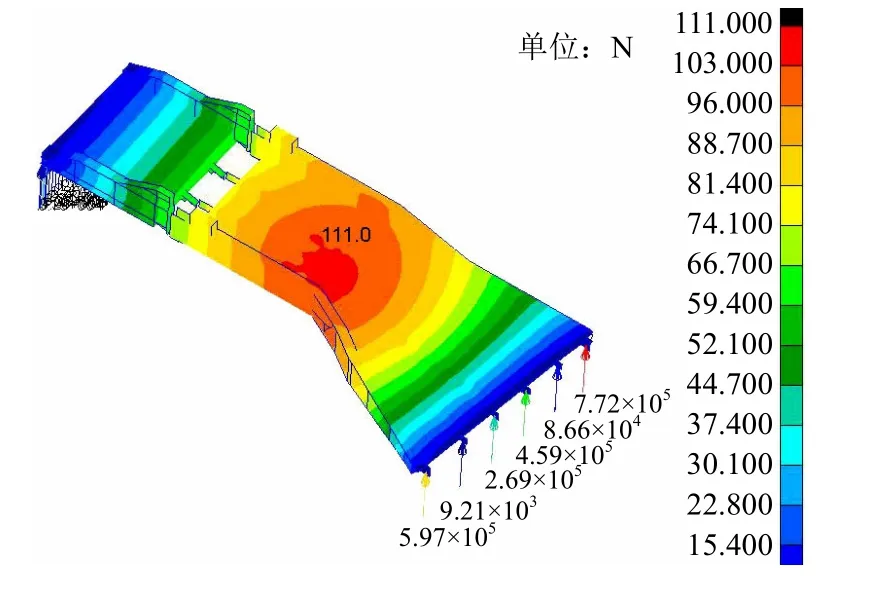
圖4 工況一下各組鉸鏈受力

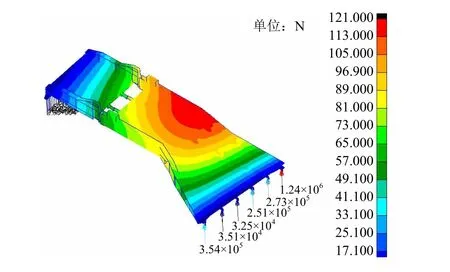
圖5 工況二下各組鉸鏈受力

表2 端部各組鉸鏈受力值 單位：kN

通過有限元計算可知，在考慮1.1倍動載荷系數的情況下，各組鉸鏈中主鉸鏈A的受力最大，在工況二中其受力最大值達1240kN。因此，在后續動力學仿真計算中，將重點分析車輛沿主鉸鏈A一側通過時主鉸鏈A的受力情況。

3.2 動力學仿真計算

3.2.1 建立實體模型

車輛跳板的工作角度為-5.0°～8.5°，本文所述模型中跳板與水平面的夾角設為8.5°。為模擬車輛從碼頭經過車輛跳板駛入船體的過程，應在ADMAS實體模型中設置碼頭、船體和車輛跳板。由于碼頭和船體僅提供車輛通行路徑，對端部鉸鏈受力沒有影響，因此在ADAMS中將模型簡化為長方體。對于車輛跳板，模型主要考慮對跳板質量和重心位置有較大影響的主體結構和起約束作用的各處鉸鏈，對局部加強結構不予考慮。對于通過跳板的車輛，由于本文只討論車輛質量的影響，因此只需模擬出車輛與跳板接觸的輪胎和對輪胎施加載荷的車軸。建立完成的ADAMS車輛跳板動力學仿真模型見圖6。

3.2.2 添加約束條件

在通過車輛跳板裝卸車輛過程中，受海浪、潮汐等外部因素的影響，車輛跳板與碼頭、船體之間可能存在相對移動

或轉動，但這種相對運動是比較緩慢的。為合理地簡化模型，可假設車輛跳板與船體、碼頭之間是相對靜止的。對于端部鉸鏈和2節跳板之間的中間鉸鏈，模型采用ADAMS約束命令中的旋轉副進行約束。ADAMS模型約束信息見表3。

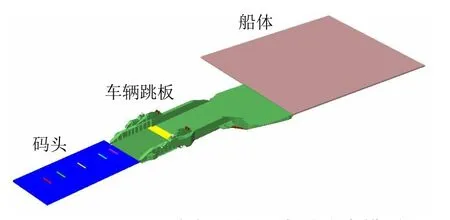
圖6 ADAMS車輛跳板動力學仿真模型

表3 ADAMS模型約束信息

3.2.3 添加接觸力

車輪與跳板之間和各組鉸鏈與鉸鏈軸之間采用ADAMS中的接觸模型定義。ADAMS中的接觸力主要考慮沖擊力和摩擦力，分別采用沖擊函數模型和庫倫摩擦力模型計算。關于接觸力的定義，需設置以下參數：

1) Force Exponent，即力的非線性指數，用來計算瞬時法向力中材料剛度項的貢獻值，表征材料的非線性特性。對于金屬，該指數常取1.3～1.5；對于橡膠，該指數可取2，甚至是3。另外，根據ADAMS幫助文件，在仿真計算中，該指數取值大于2.1通常會使碰撞模型的求解更加穩定合理。綜上，本文中該指數取系統默認值2.2。

2) Damping，即阻尼系數，用來表征接觸過程中的能量損失。該系數通常取剛度值的0.1%～1.0%，一般取10～100N·s/mm，本文中取系統默認值10 N·s/mm[7]。

3) Penetration Depth，即定義全阻尼（full damping）時的最大穿透深度。理論上該數值越小越逼近真實，但該值過小會影響ADAMS數值的收斂性，一般可取ADAMS推薦的0.1mm[8]。

與摩擦力有關的設置包括靜摩擦因數、動摩擦因數、靜摩擦轉換速度和動摩擦轉換速度。由于摩擦力的方向平行于車輛跳板頂板，對本文研究的垂向力的大小影響不大，因此與摩擦力有關的設置均取系統默認值，即靜摩擦因數0.3，動摩擦因數0.1，靜摩擦轉換速度100mm/s，動摩擦轉換速度1000mm/s。

3.3 動力學仿真結果分析

3.3.1 不同車型影響

分別計算150t重型車和90t中型車以10km/h的速度通過跳板時主鉸鏈A的受力情況，結果見圖7和圖8。

圖7 10km/h車速下150t車輛主鉸鏈A受力

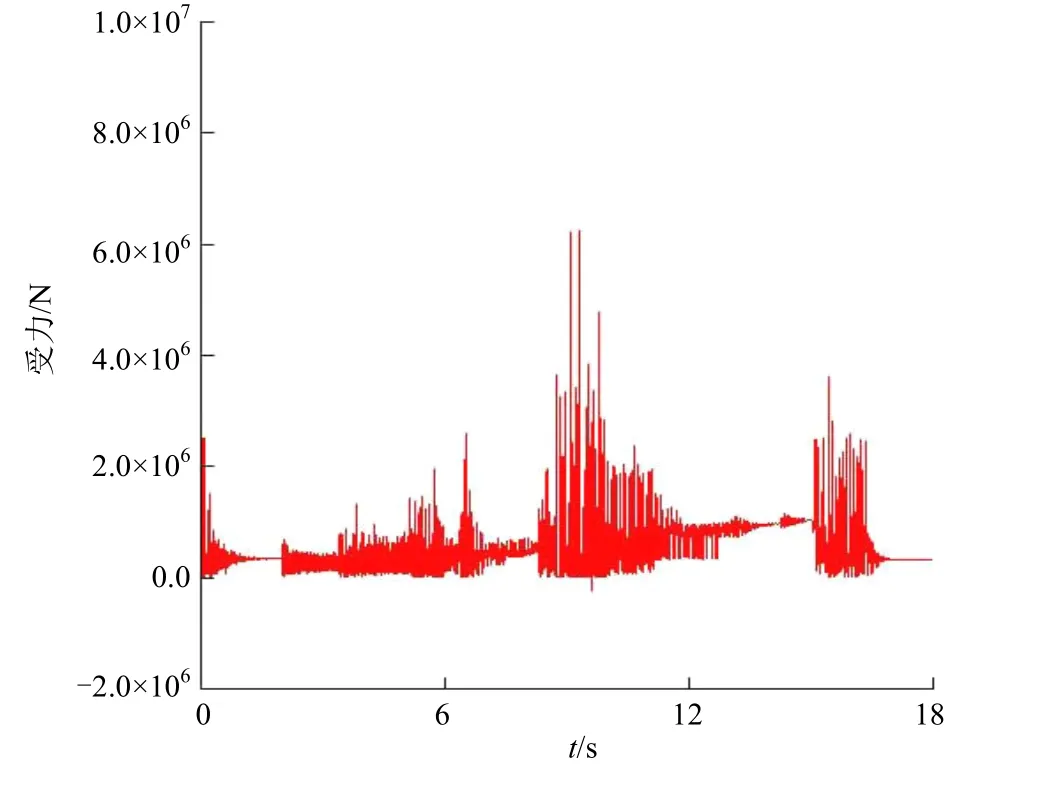
圖8 10km/h車速下90t車輛主鉸鏈A受力

根據動力學仿真計算，車輛載荷的實際作用有以下2個特點：

1) 車輛載荷會對鉸鏈產生大于1.1倍動載荷的作用；

2) 車輛載荷不是靜載荷，而是動態循環載荷。

對于跳板長度很長的大型PCTC而言，在采用靜力學方法進行強度校核時，由于跳板與碼頭之間的摩擦力在鉸鏈處產生的作用力一般大于車輛載荷對鉸鏈的作用力，因此對于鉸鏈的設計而言，危險載荷往往是摩擦力，而不是車輛載荷。另外，船級社規范中滾裝設備部件的許用應力遠小于材料的屈服強度，因此對于車輛載荷而言，鉸鏈的安全裕度是很大的。

但是，根據圖 7所示的計算結果，鉸鏈的最大受力約為6.86×103kN，已遠遠超過摩擦力在鉸鏈處產生的作用力。剖面形狀見圖9，則其平均應力τ= 239 MPa 。若考慮使用過程中的磨損、銹蝕等情況，重型車通過跳板時產生的動載荷是比較危險的，僅按傳統計算方法無法真實體現出鉸鏈受力的最不利情況。綜上所述，在設計鉸鏈時應留有足夠的安全余量，以避免車輛通過跳板過渡區域時產生的瞬時動載荷對結構造成不利影響。另外，對于裝載量巨大的大型汽車滾裝船而言，由于車輛載荷實際上是循環載荷，因此鉸鏈可能會發生疲勞破壞。由此可見，僅對鉸鏈的靜強度進行校核未必能全面衡量其安全性，采用動力學方法對鉸鏈的強度進行分析十分必要。

圖9 主鉸鏈A外形圖

3.3.2 不同車速影響

分別計算150t重型車以15km/h和20km/h的速度通過跳板時主鉸鏈A的受力情況，結果見圖10和圖11。

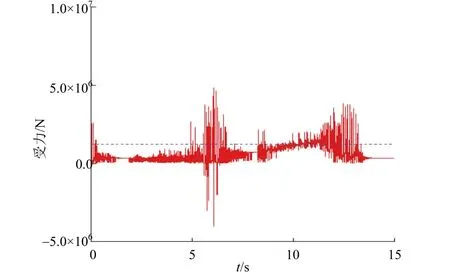
圖10 15km/h車速下150t車輛主鉸鏈A受力

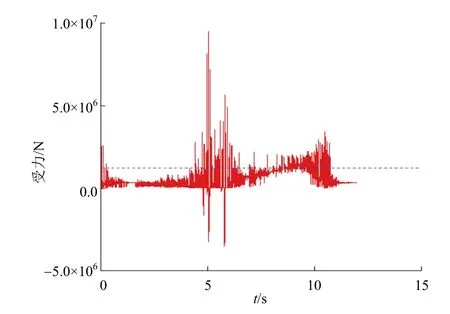
圖11 20km/h車速下150t車輛主鉸鏈A受力

由計算結果可知，車輛以15km/h和20km/h的速度通過跳板時，主鉸鏈A受力的平均值比以10km/h的速度通過跳板時更大，因此動載荷系數也大于1.1。由于重型車輛總重很大，為防止其產生的動載荷對結構產生不利影響，在滾裝船裝卸車輛過程中，應嚴格控制重型車的車速，以免發生意外。

3.3.3 多種車型組合

分別計算3輛重型車和重型車+中型車+小型車這2種工況下3輛車連續以15km/h的速度通過跳板時主鉸鏈A的受力情況，結果見圖12和圖13。在控制車輛通過跳板時，前后2輛車會在一段時間內同時行駛在跳板上，因此其載荷會產生一定的相互影響。由仿真結果可知，3輛車先后經過跳板形成的載荷譜并不是每種單一車型通過跳板時形成的載荷譜的疊加。這種相互影響也是采用靜力學方法難以模擬分析的。

圖12 15km/h車速下車輛主鉸鏈A受力（重型車+重型車+重型車）

圖13 15km/h車速下主鉸鏈A受力（重型車+中型車+小型車）

由第 3.3.1節的分析和本節的計算結果可知，車輛載荷對跳板鉸鏈的影響是十分復雜的。大型 PCTC單個航次內可能有數以千計的車輛通過車輛跳板完成裝卸，車輛跳板承受循環載荷的次數可能會達到數十萬次，其全壽命周期內的載荷循環次數可達107～108量級。根據疲勞強度理論，鉸鏈并不一定在跳板全部

通過重型車的情況下破壞，僅以最大載荷來分析鉸鏈的強度是不全面的。因此，隨著汽車滾裝船裝載量和裝載車輛總重的不斷增加，應按上述方式建立不同車型組合通過跳板時鉸鏈受力的載荷譜，以便進一步分析鉸鏈在高應力循環次數和高平均應力條件下的疲勞強度。

綜合上述計算，采用動力學方法計算車輛載荷作用下鉸鏈的受力，可得到很多采用靜力學方法計算無法得到的結果，二者之間的主要差異見表4。

表4 動力學方法與靜力學方法計算結果對比

4 結 語

本文研究了汽車滾裝船跳板設計分析中鉸鏈的靜載荷和動載荷，分析了車輛對跳板產生的動載荷。首先，采用有限元分析軟件MSC·PATRAN計算得到了某巴拿馬級PCTC車輛跳板在車輛載荷作用下鉸鏈受力的最大值。隨后，針對受力最大的主鉸鏈A，采用多體動力學仿真軟件MSC·ADAMS建立了動力學仿真模型，得到了不同車型和車輛以不同車速通過跳板時主鉸鏈的動載荷，并與PATRAN的計算結果進行了對比。

通過靜力和動力對比分析可知：采用靜力分析結果的1.1倍來考慮動載荷不合適，需考慮車輛的動態作用；動力學方法既可用來校核鉸鏈的靜力學強度，又可根據計算得到的載荷譜為鉸鏈的疲勞強度分析提供計算依據，相比傳統的靜力學方法，可使鉸鏈的強度分析更全面。