考慮磁致伸縮效應的永磁同步電機磁-機械耦合模型

夏 林，于慎波，竇汝桐，夏鵬澎

(沈陽工業大學 機械工程學院，沈陽 110870)

0 引 言

為了使電機滿足某些特殊應用場合的要求，尤其在軍工和家用電器領域，對電機的振動噪聲指標的要求近乎苛刻，越來越多的學者研究電機的振動噪聲問題。電機振動噪聲的來源主要有機械噪聲、空氣噪聲和電磁噪聲三個方面，目前普遍認為電磁力是電機電磁振動噪聲的主要激勵源，但忽略了磁致伸縮效應的影響[1-2]。磁致伸縮效應是鐵磁材料的固有屬性，且對外部應力變化特別敏感，磁致伸縮是指鐵磁材料在磁化狀態下會沿著磁場方向發生伸長或縮短，這個應變不同于其他由機械或電磁應力而產生的應變[3]。在低頻條件下，在船舶潛艇等軍用裝備中，磁致伸縮效應可能會顯著加劇振動噪聲幅值。

2002年，美國佛羅里達州大學的Mohammed教授建立了考慮磁致伸縮效應的電機定子鐵心的磁-彈性模型，通過數值計算分別得出了考慮磁致伸縮效應和電磁力單獨作用時電機定子鐵心齒部所受應力，在考慮磁致伸縮效應時，齒部應力與電磁力單獨作用相比增加了50%[5-6]。2009年，英國Sakda Somkun教授與其學生對考慮磁致伸縮效應各向異性情況下的電機定子鐵心的振動變形進行了研究，與普通計算結果相比，考慮磁致伸縮各向異性時的計算結果更加接近電機實際工作情況，有效地提高了電機仿真計算的精確程度[7]。

近年來，國內對于磁致伸縮效應研究也不斷增加。文獻[1]研究了磁致伸縮效應對變壓器振動噪聲的影響，建立了變壓器鐵心磁-機械耦合模型，研究結果表明，磁致伸縮效應時的振動噪聲結果比實際工作情況誤差更小。沈陽工業大學張艷麗教授及其研究團隊對旋轉磁化條件下、直流偏磁條件下和諧波磁場下的硅鋼片磁致伸縮特性進行了研究[8]。文獻[9-10]研究了變頻器供電條件下永磁電機的振動噪聲問題，實驗結果表明，隨著供電電流頻率的提高，電機振動噪聲也會隨之增大。文獻[11]通過線性壓磁方程來建立考慮磁致伸縮效應的解析計算模型。

1 建立數學模型

1.1 定子磁場分析

根據麥克斯韋方程，建立電機定子鐵心磁場模型：

×H=J

(1)

(2)

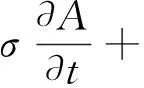
(3)

B=×A

(4)

式中：H為磁場強度；e為電場強度；B為磁通密度；σ為電導率；A為磁矢量勢；J為外部電流密度。

1.2 磁致伸縮力的計算

在計算磁致伸縮力的過程中，假設定子鐵心材料變形均勻且完全服從胡克定律，則磁致伸縮應力：

Fms=G·P

(5)

式中：G為彈性矩陣；P為磁致伸縮應變。

假設材料呈現各向同性，彈性矩陣G可由材料的彈性模量和泊松比表示，對于二維平面應變問題，則有：

(6)

式中：E為材料的彈性模量；α為材料的泊松比。

磁致伸縮應變P通過磁通密度B向定子鐵心材料的B-P磁致伸縮特性曲線插值得到，材料的磁致伸縮特性曲線如圖1所示。

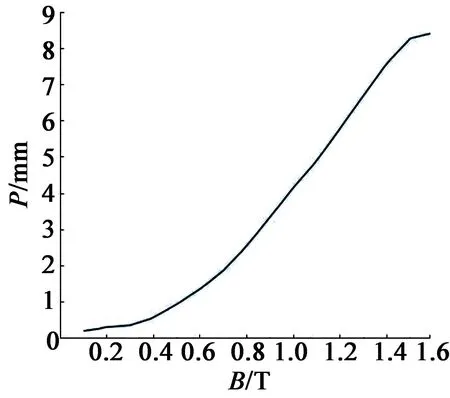
圖1 硅鋼片磁致伸縮特性曲線

1.3 耦合模型的建立

永磁同步電機系統的總能量W由彈性能U1和磁場能U2兩部分組成：

(7)

式中：u為定子振動位移；K為機械剛度矩陣；A為磁矢量勢；M為磁場剛度矩陣。

由于能量項的類似形式，采用式(7)的方程組來表示耦合的磁-機械系統：

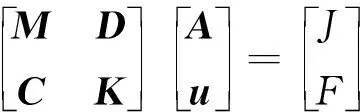
(8)

式中：F表示與電磁無關的外部力；C，D表示耦合項，耦合項C表示磁場對于機械振動位移的作用，耦合項D表示定子振動位移對磁場的影響。

為了簡化磁機械耦合系統，用機械系統總能量分別對振動位移u、磁矢量勢u求偏導，則有：

(9)

結合式(8)和式(9)可得：

(10)

用彈性能U1對磁矢量勢A求偏導，且用磁場能U2對定子振動位移u求偏導，則有：

(11)

由于在小型電機中忽略了電機尺寸的微小形變對磁場分布的影響，所以采用弱耦合的方式，即耦合項D為0；耦合項C表示磁場對于機械振動位移的影響，所以C右乘磁矢量勢A即可得電磁力：

Fmag=-CA

(12)

因此磁-機械耦合系統轉變：

(13)

現在，在分析工程中用磁致伸縮力Fms來表示磁致伸縮效應，磁致伸縮力可以直接加到外部力F和電磁力Fmag上[12]，則考慮定子鐵心硅鋼片磁致伸縮效應的耦合模型：

(14)

2 定子鐵心有限元分析

本文的研究是將磁-機械耦合問題看作是弱耦合問題，在弱耦合問求解中，先計算單元的電磁力、磁致伸縮力和機械應力，再通過這些來計算定子齒部的振動位移[13-14]。

本文的永磁同步電機模型為8極36槽的表貼式永磁電機，通過有限元仿真軟件建立定子鐵心磁-機械耦合模型，并對電機振動噪聲進行仿真研究。電機在工作過程中的主要工作參數如表1所示。由于永磁同步電機的均勻對稱性，為了方便對其進行仿真分析，減少計算機的工作量，提高計算效率，本文采用二維平面模型對其進行仿真計算分析。二維平面模型圖和計算參考點如圖2所示。

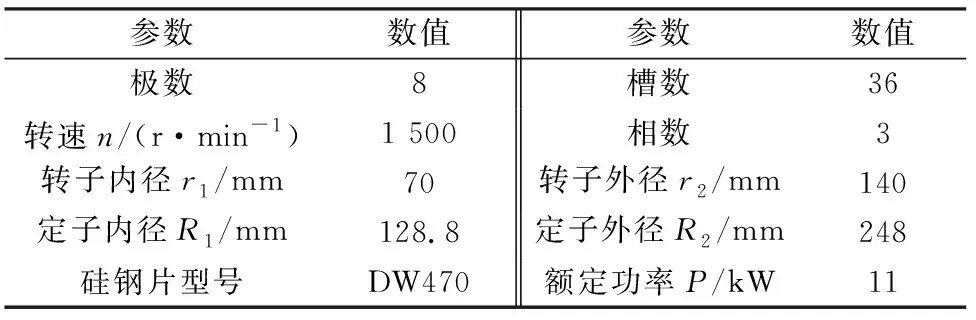
表1 電機主要參數

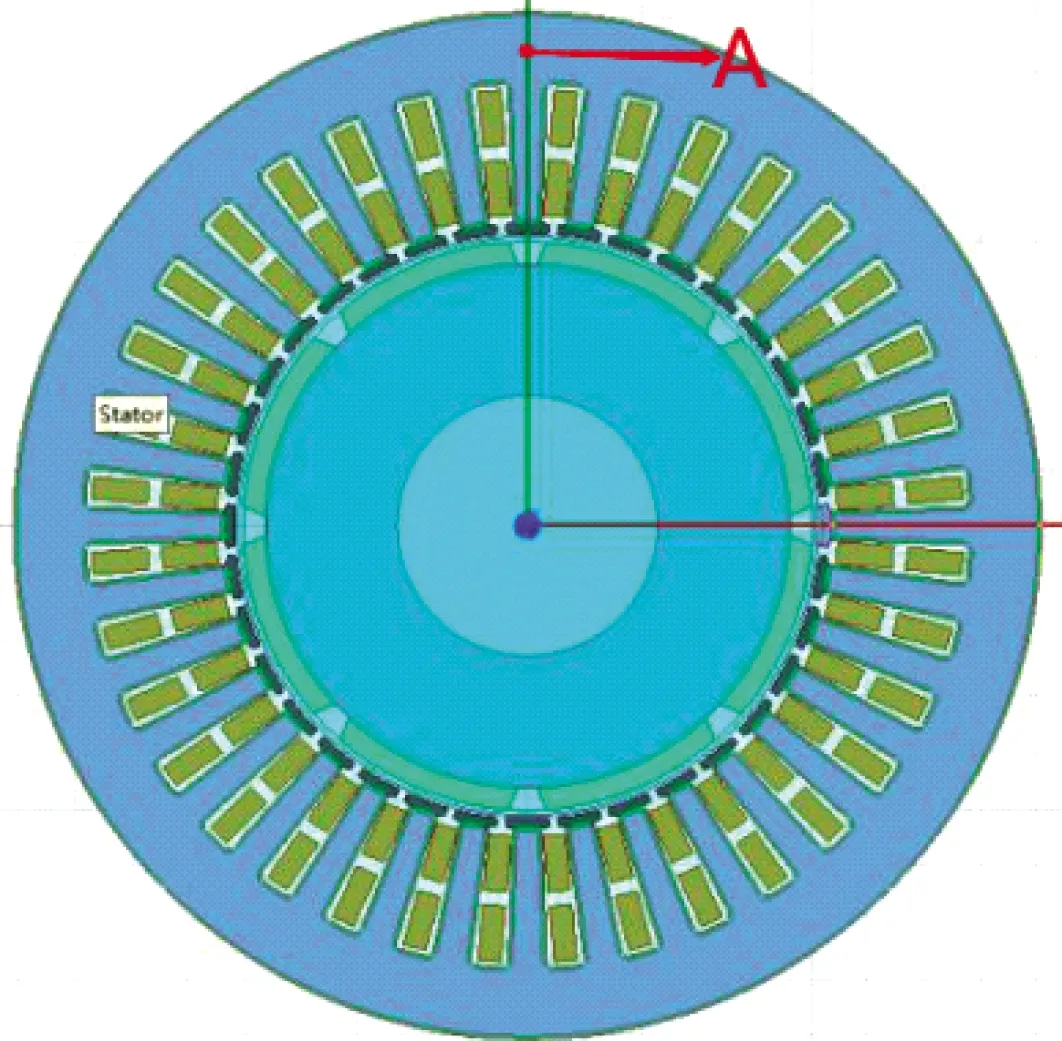
圖2 電機二維模型圖

在有限元仿真過程中：首先通過ANSYS Maxwell對電機二維模型進行電磁場仿真，得到如圖3所示的電機磁通密度分布云圖和定子齒尖電磁力等相關數據；其次，在MATLAB中根據得到的磁通密度B向硅鋼片磁致伸縮特性曲線插值計算得到磁致伸縮應變、磁致伸縮力等數據；最后將電機定子的三維模型導入ANSYS Workbench中，分別對電磁力單獨作用時、考慮磁致伸縮效應時電機定子的振動噪聲響應進行仿真。

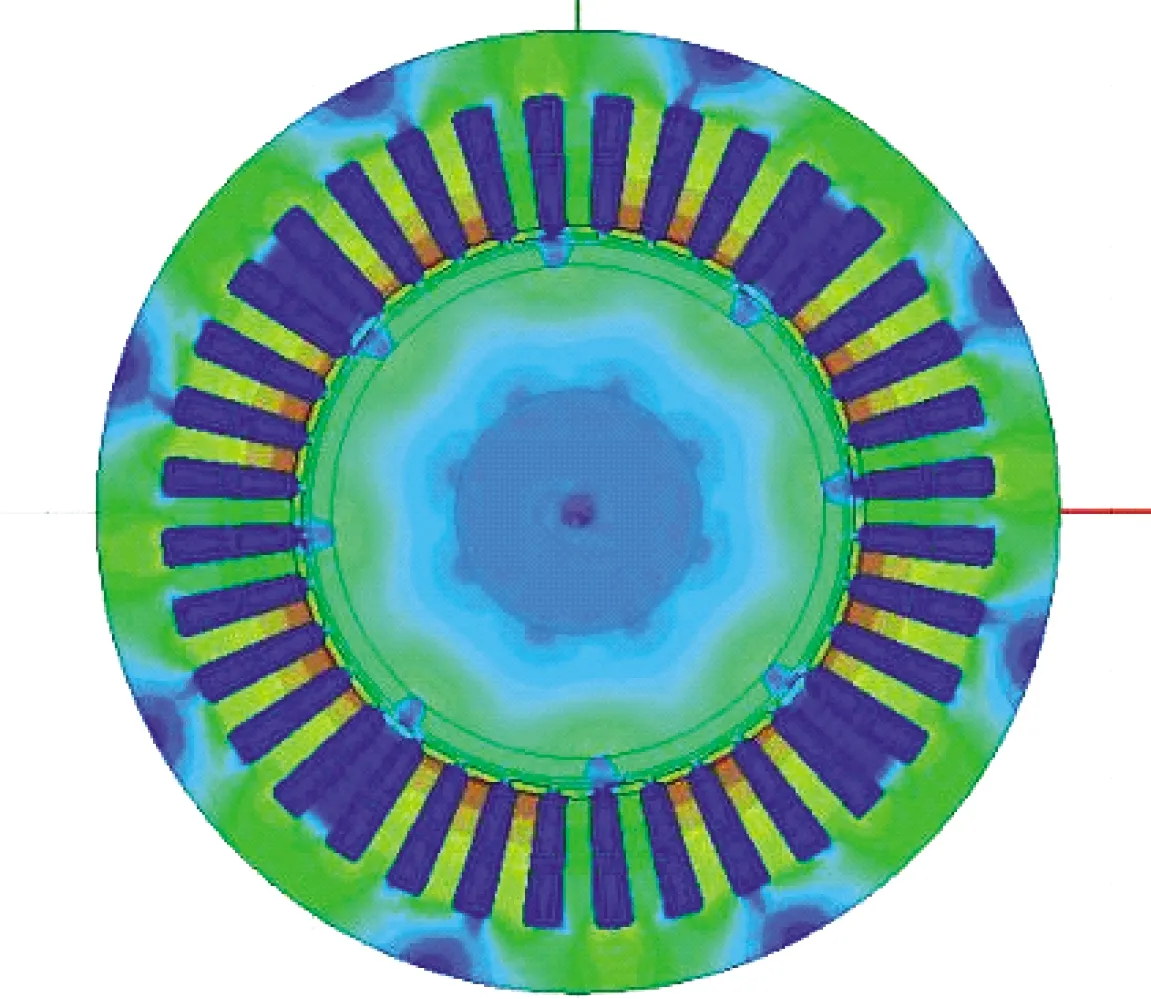
圖3 永磁電機磁通密度分布云圖

將Maxwell計算出的徑向磁通密度數據導出到MATLAB中，然后根據圖1的磁致伸縮特性曲線插值得到定子鐵心的磁致伸縮應變，并結合式(5)計算考慮磁致伸縮效應而產生的磁致伸縮力，如圖4所示。圖5和表2展示了考慮磁致伸縮效應時和電磁力單獨作用時的定子齒徑向電磁力密度，為了方便觀察，取半個電周期的數據作為參考。

由圖4、圖5和表2可以看出，磁致伸縮效應對定子鐵心的振動噪聲確實存在不可忽略的影響，在磁致伸縮效應作用下，定子齒徑向力密度的幅值增加了13.1%，平均值增加了25%。

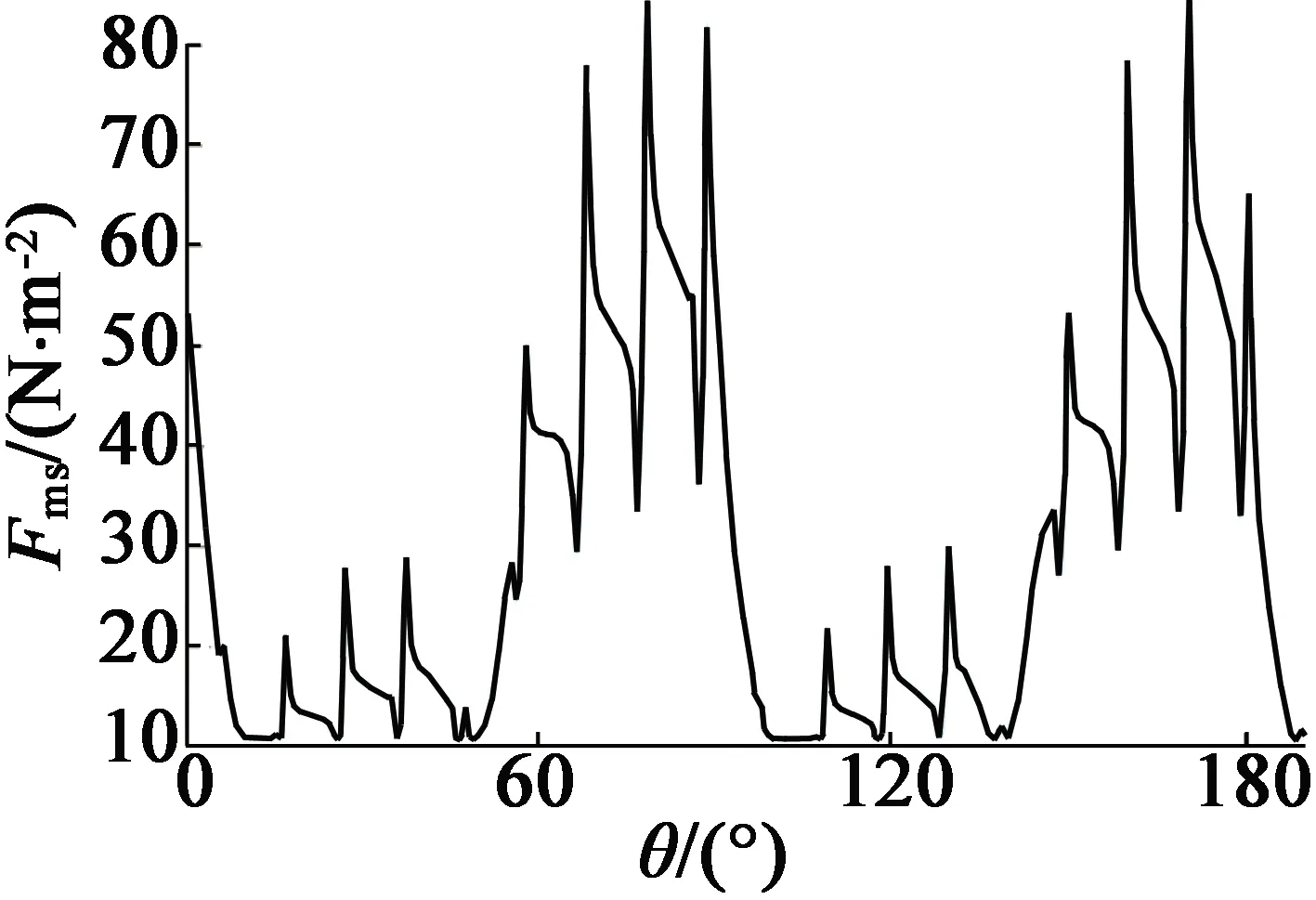
圖4 定子齒徑向磁致伸縮力密度圖

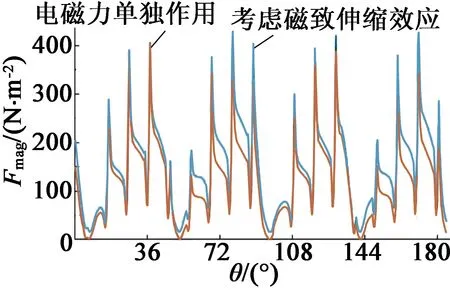
圖5 定子齒徑向力密度圖

表2 徑向電磁力密度參數

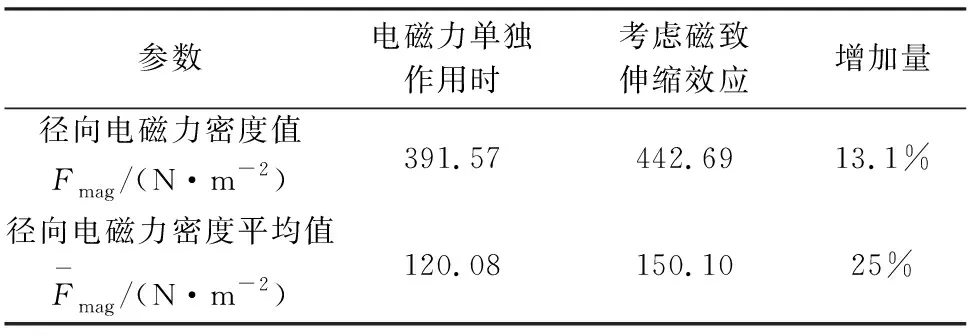
參數電磁力單獨作用時考慮磁致伸縮效應增加量徑向電磁力密度值Fmag/(N·m-2)391.57442.6913.1%徑向電磁力密度平均值F-mag/(N·m-2)120.08150.1025%

將圖5兩種情況下的徑向力密度數據依次作為外加載荷在ANSYS Workbench中加到定子齒表面，以進行磁-機械耦合的諧響應計算。圖6(a)和圖6(b)分別給出了單獨考慮電磁力和考慮磁致伸縮效應作用下定子鐵心表面應變分布情況，為了強化視覺效果，縮放比例為106。

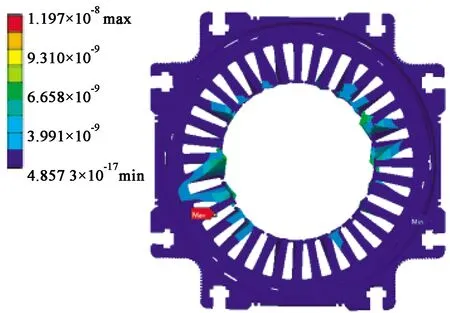
(a) 電磁力單獨作用

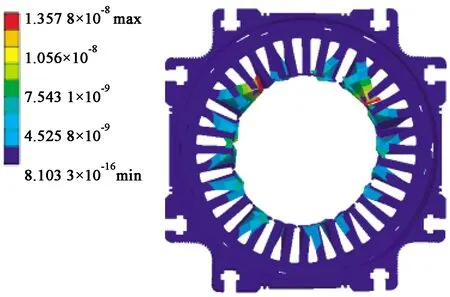
(b) 考慮磁致伸縮效應

對比圖6(a)和圖6(b)可以發現，在考慮磁致伸縮效應時，定子鐵心的變形量均比電磁力單獨作用有所增加，齒部的最大變形比電磁力單獨作用時增加了13.4%，說明磁致伸縮效應對于永磁同步電機定子振動噪聲的影響是真實存在的。

為了更加真實地反映定子的振動特性，對定子鐵心進行諧響應分析。選擇定子軛部一定點A，計算在電磁力單獨作用時和考慮磁致伸縮效應時該點的振動速度，得出的諧響應分析結果如圖7所示。

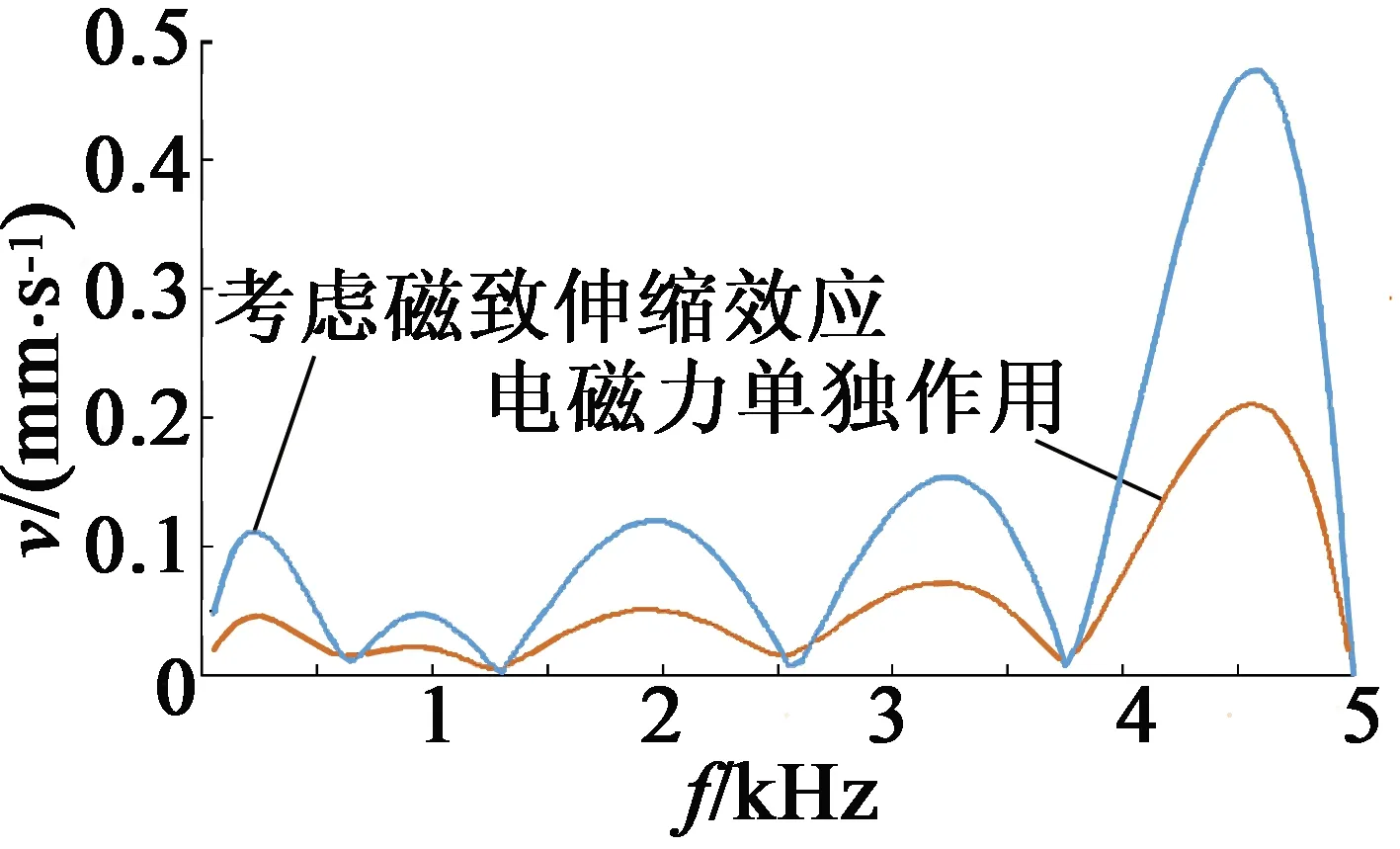
圖7 A點振動速頻譜圖

由圖7諧響應分析對比中可以看出，在考慮磁致伸縮效應時，A點的振動速度明顯增加，振動速度最大值與電磁力單獨作用時相比增加了1.23倍。

在諧響應分析的基礎上，通過ANSYS Acoustic模塊對電機定子鐵心的噪聲響應進行了分析與計算。首先在電機外建立一個半徑1 m的空氣包作為聲場響應計算區域，得出電磁力單獨作用、考慮磁致伸縮效應的聲壓級曲線，如圖8所示。

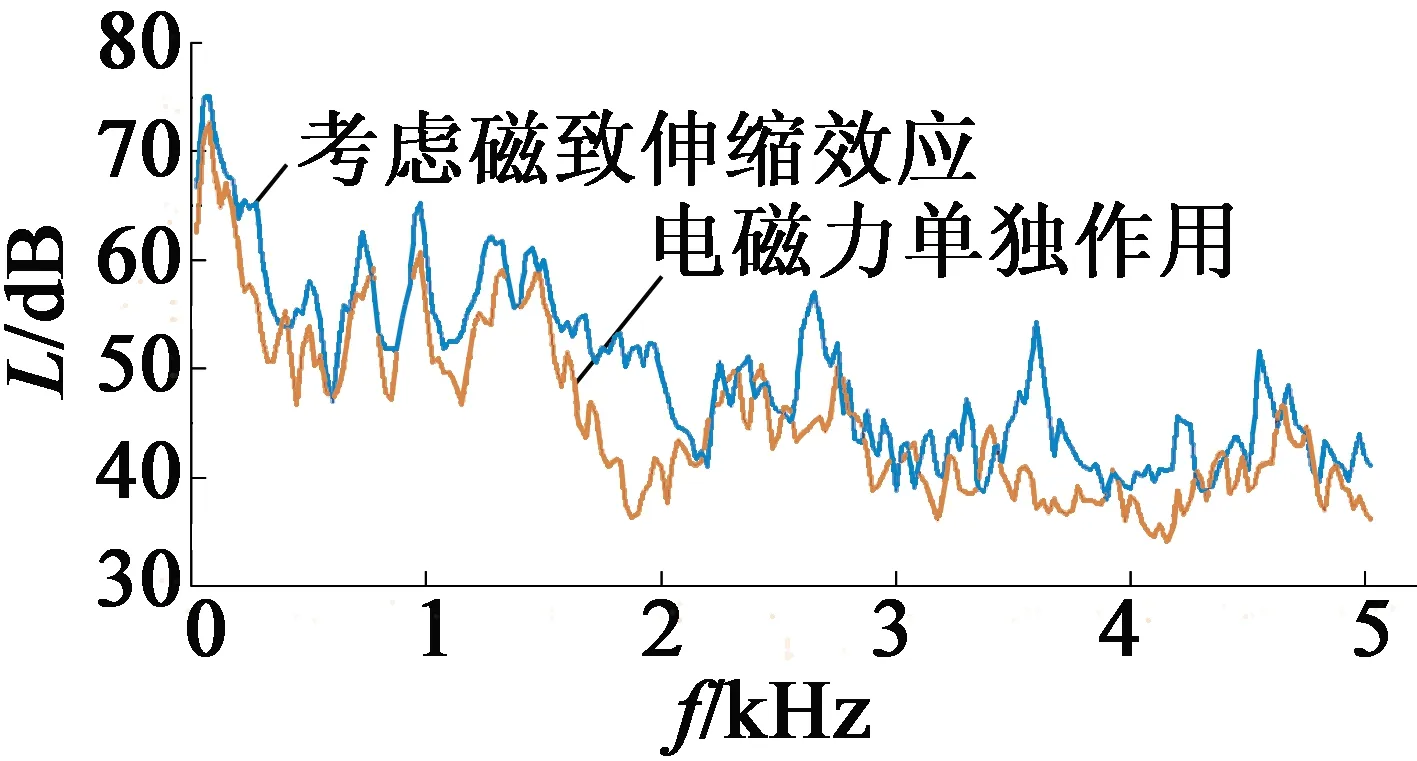
圖8 考慮磁致伸縮效應和電磁力單獨作用時聲壓級曲線

通過圖8的噪聲聲壓曲線可以看出，考慮磁致伸縮效應時，定子周圍的噪聲明顯大于電磁力單獨作用時的噪聲。

3 結 語

本文建立了電磁-機械耦合數值模型，并在有限元軟件中進行仿真，分別對永磁同步電機在電磁力單獨作用時和考慮磁致伸縮效應下進行了振動仿真，并得出了以下結論：

在磁致伸縮效應的作用下，定子齒徑向力密度幅值和最大齒部變形比電磁力單獨作用時分別增加了13.1%和13.4%，且振動速度的最大值增加了1.23倍，聲壓級分布也明顯增大。因此，磁致伸縮效應對于電機振動有重要貢獻。為了在特殊場合滿足永磁同步電機對振動噪聲的要求，在電機設計計算階段應考慮磁致伸縮效應。