永磁同步電機滑模觀測法轉子位置檢測

包廣清，王 濤

(1.蘭州理工大學 電氣工程與信息工程學院，蘭州 730050；2.蘭州理工大學 甘肅省工業工程先進控制重點實驗室，蘭州 730050)

0 引 言

近年來,永磁同步電機(以下簡稱PMSM)因體積小、噪聲低、質量輕、運行可靠等優點[1]，在人們的日常生活及其國家的工農業等方面都得到了廣泛的使用。為了更好地控制電機，需要知道電機轉子準確的位置和轉速。最初獲取轉子位置的方法主要是通過安裝機械轉子位置傳感器[2]，如霍爾傳感器、磁阻傳感器、電渦流式傳感器等，但是這些設備的安裝增加了系統的成本，提高了對工作環境的要求，電機整體設備也變得非常復雜，最終導致電機的可靠性降低[3]。因此，無速度傳感器方法開始受到大量學者的關注與研究。

目前，PMSM無傳感器檢測法主要有兩種：一種是外加激勵信號的方法[4]，即根據電機的凸極效應，給電機繞組中通入激勵信號，通過分析其響應信號提取轉子位置，該方法比較適用于電機起動及低速運轉時轉子及轉速的提取，如脈振高頻信號注入法[5]；另一種是不外加激勵信號的方法，即直接根據電機反電動勢提取包含轉子位置的信號，這種方法適用于電機高速工作情況。不外加激勵信號的方法一般有狀態觀測器法[6]、基于磁鏈的估計方法[7]、模型參考自適應方法[8]、擴展卡爾曼濾波器(Extended Kalman Filter, EKF)[9]、模糊控制[10]、滑模變結構控制[11]等。狀態觀測器法需要獲得系統的全部狀態信息，但是系統的狀態變量不一定都能直接測量到，即使有些變量可測,所需的傳感器價格也較高，增加了系統的成本與復雜性[12]。模型參考自適應法對控制系統中電機的參數依賴性非常高。模糊控制是對檢測到的信息進行模糊處理，這個過程會降低系統的控制精度，并且控制器的設計尚缺乏系統性[13]。滑模變結構通過不停地改變控制器的結構來實現系統的不間斷控制，這種方法受到系統參數和外界干擾的影響較小，最后測量得到的結果誤差也比較小。但是傳統的滑模變結構觀測法所使用的開關函數和低通濾波器會產生抖振大、電機中大量諧波無法消除等問題，系統測量得到的轉子位置準確性大大降低。

針對以上提到的傳統滑模觀測器中的兩種問題，前人提出對系統的開關轉換函數進行優化，使系統的開關函數趨近平滑，從而削弱抖振。本文在傳統滑模變結構觀測法檢測轉子位置信息的基礎上，引入卡爾曼濾波器，利用其濾波能力的同時去逼近未知模型參數，適當擴大解空間的搜索范圍，避免了不必要的系統誤差，可以濾除系統中的大量諧波。兩種方法都能相應地減弱抖振，達到優化傳統滑模觀測器的目的。最后通過仿真建模，來對比PMSM在優化前后對電機轉子位置檢測的不同結果。

1 電機數學模型

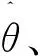
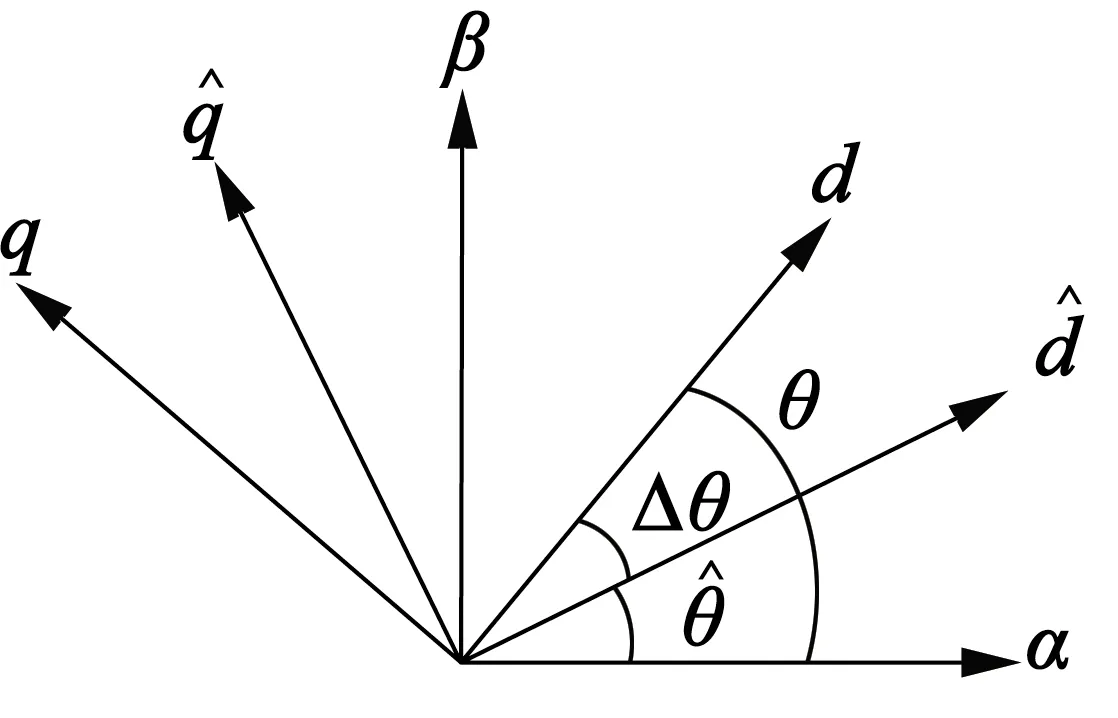
圖1 各坐標系關系

PMSM在兩相靜止坐標系即α，β坐標系中的數學模型：

(1)

反電動勢在兩相靜止坐標系下的數學模型：

(2)

式中：iα與iβ分別是定子電流在靜止坐標系α，β軸中的分量；Uα與Uβ分別是定子電壓在靜止坐標系α，β軸中的分量；eα與eβ分別是反電動勢在靜止坐標系α，β軸中的分量；R為定子電阻；ψf為轉子磁鏈；ωr為轉子角速度；L為定子電感；θ為轉子位置角。

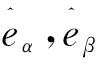
(3)

(4)

傳統的滑模觀測器機構圖如圖2所示。

圖2 傳統滑模觀測器結構圖

2 傳統滑模觀測器滑模面改進措施

非線性的滑模變結構控制在1950年左右被提出,其突出特點是對控制的不連續性，即對控制系統的結構不固定。并且在系統的狀態改變時，非線性滑模控制的運動狀態可根據系統的變化做出相應調整，不受系統狀態變化的影響，可以很好地解決非線性系統問題。

如圖3所示，設s(x)為一個切換面。

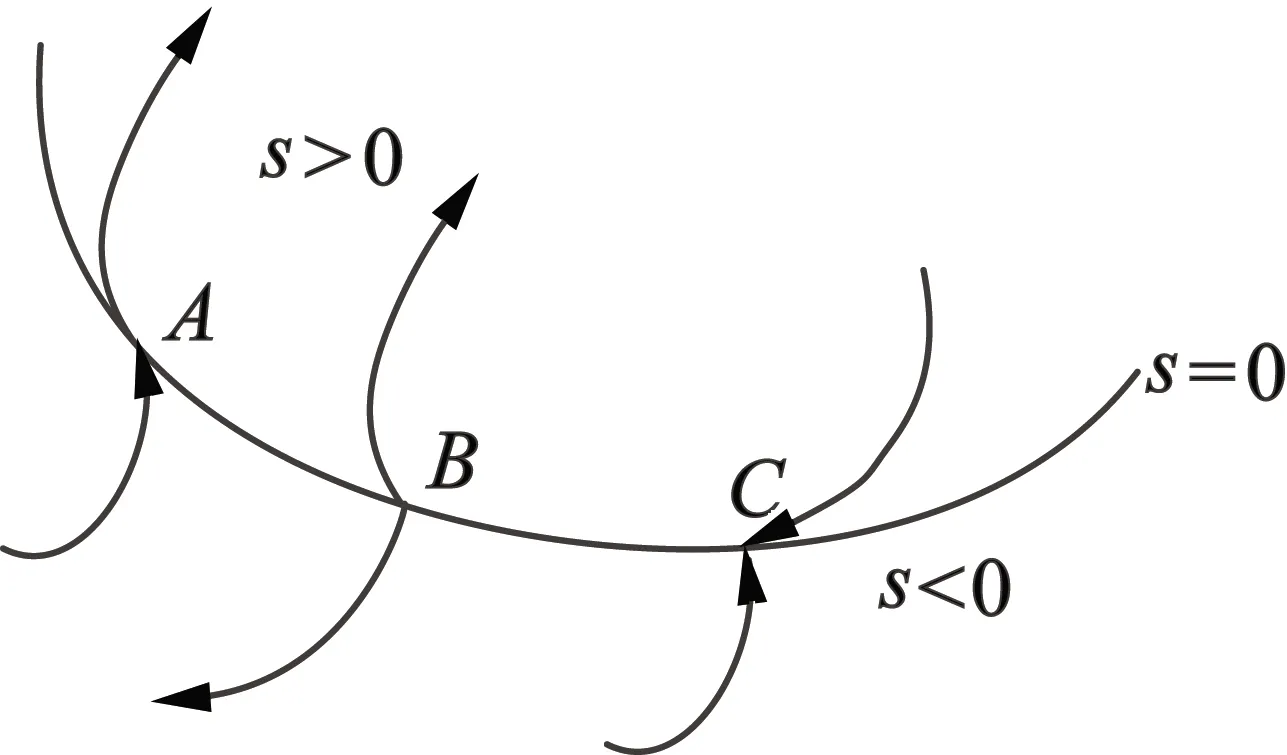
圖3 切換面上三種不同的點

(5)

(1) A類：系統從遠離曲面開始出發，運動到滑模面附近，然后穿過滑模面最后遠離滑模面，稱為普通點；

(2) B類：系統運動到滑模面附近，并且向兩邊遠離滑模面，稱為起始點；

(3) C類：系統運動到滑模面附近，并且從兩邊趨近于該點，稱為終止點。

如果在該曲面的某一片范圍內存在的均為C類終止點，則將這片區域稱為滑模區，該點的運動狀態稱為滑模運動。

若知道系統的狀態方程：

(6)

式中：x為系統狀態；u為控制變量；t為時間。

有合適的切換函數s(x),x∈R,則有控制量u：

(7)

式中：u+(x)≠u-(x)。

結合以上PMSM數學模型以及滑模變結構，傳統的滑模觀測器通常設計如下：

(8)

式中：

(9)

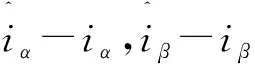
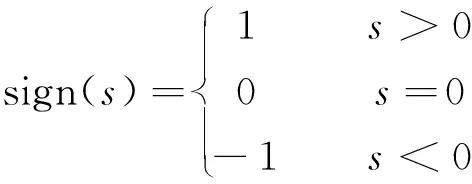
(10)

將式(8)與式(1)做差，得到系統的動態偏差：

(11)

(12)

將式(12)代入式(3)與式(4)，就可以估算出轉子位置和轉速信息。

傳統的滑模控制為了使系統達到穩定狀態，必須要維持滑模態運動并且要產生無限的切換控制。在實際的滑模控制系統中，控制開關和測量方式存在客觀局限性，并且選取的是具有不連續性質的控制開關函數，并不能實現理想中的無限快的切換控制條件，會導致系統產生比較嚴重的抖振現象。因此，可以通過改進開關切換函數來消除一部分抖振對系統的影響。

對于上述提到的抖振問題，在一個實際的現變結構系統中，一些理想狀態是不可能完全都成立的，抖振會使系統的耗能增加，還會使系統的控制精度降低，甚至更嚴重的情況下有可能使整個系統振蕩或者失穩。考慮到開關函數的快速切換引起的不連續控制是抖振發生的根本原因，提出采用sigmoid函數取代sign函數來削弱抖振現象。

(13)

式中:k為觀測器的增益系數；a為連續函數的斜率且a>0，其中a值越小，連續函數的曲線越光滑，系統的抖振也會越小，反之，a值越大，系統的抖振也越劇烈。sigmoid函數的曲線如圖4所示。

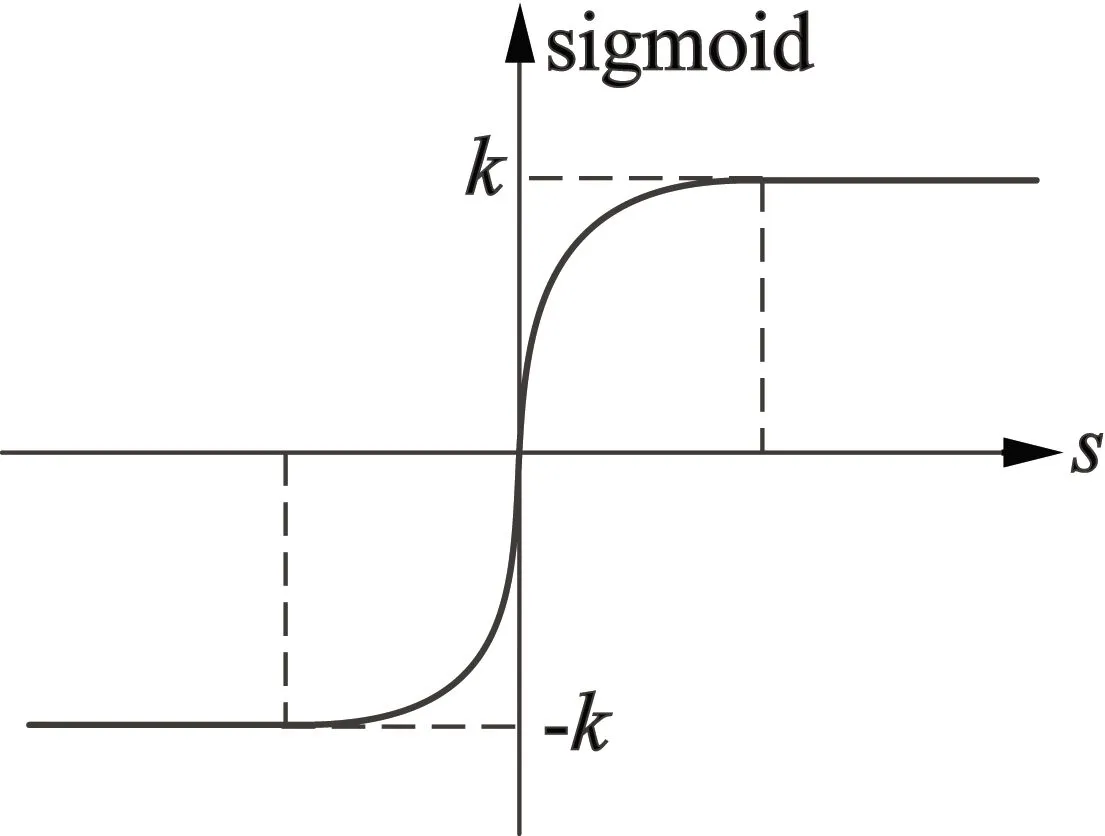
圖4 sigmoid函數

采用sigmoid函數表達式：

(14)

3 基于滑模觀測器的卡爾曼濾波器

傳統的滑模觀測器在得到zα，zβ后，其中有電機轉子位置信息和高頻諧波，傳統方法是通過低通濾波器來消除控制信號中存在的大量諧波，得到比較平滑的開關信號，也可以減弱系統抖振現象。但是低通濾波器在滑模觀測器中的使用會引起系統相位偏移，并且也不能有效濾除系統中的諧波和擾動，最后得到轉子位置的誤差也較大，對系統的估測精度有較大的影響。改進方法是選擇在低通濾波器之后再引入擴展卡爾曼濾波器，卡爾曼濾波器是一種實時的遞推算法，即使系統中有很大的噪聲和擾動，最后依然可以得到一個比較準確的估計值。改進方法的核心是利用觀測得到的反饋值來修正預測值，慢慢逼近真實值。本文要處理的噪聲也是系統噪聲，現實中的噪聲大都符合高斯噪聲的正態分布特性，如圖5所示。

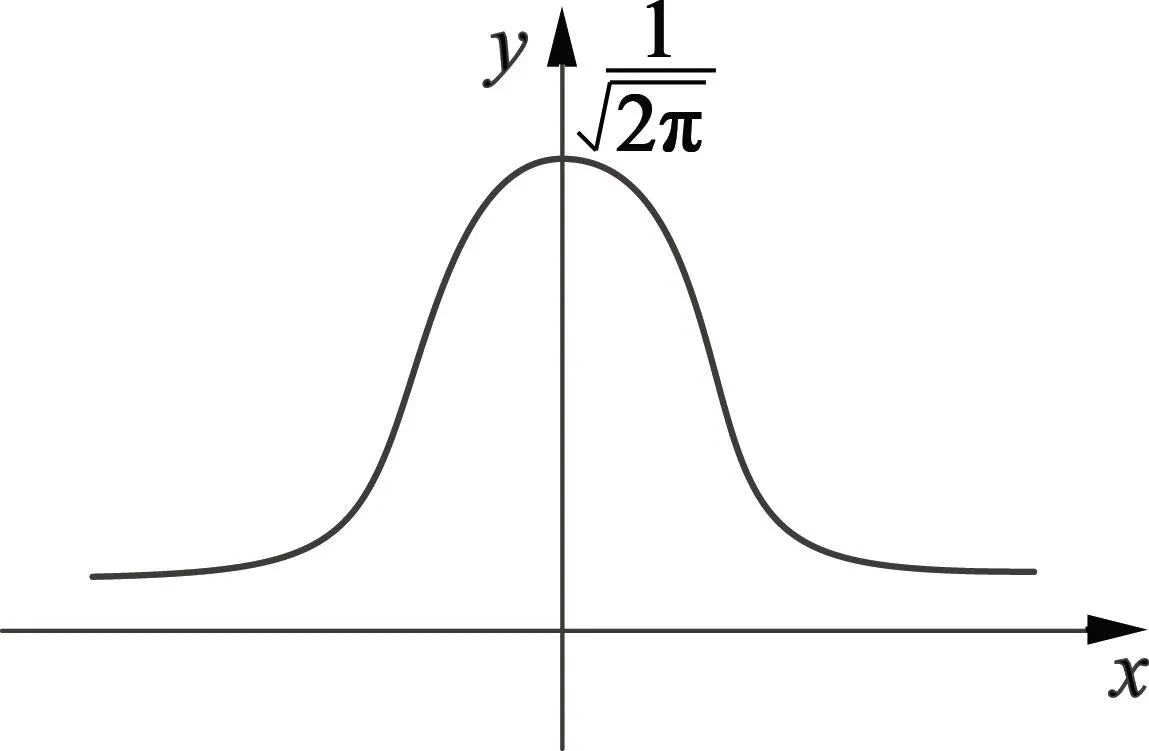
圖5 高斯噪聲的正態分布特性

卡爾曼濾波器首先在某一隨機時刻進行估計，然后再用測量得到反饋值進行校正。如圖6所示，將卡爾曼濾波器分為兩個部分，即時間更新和狀態更新。

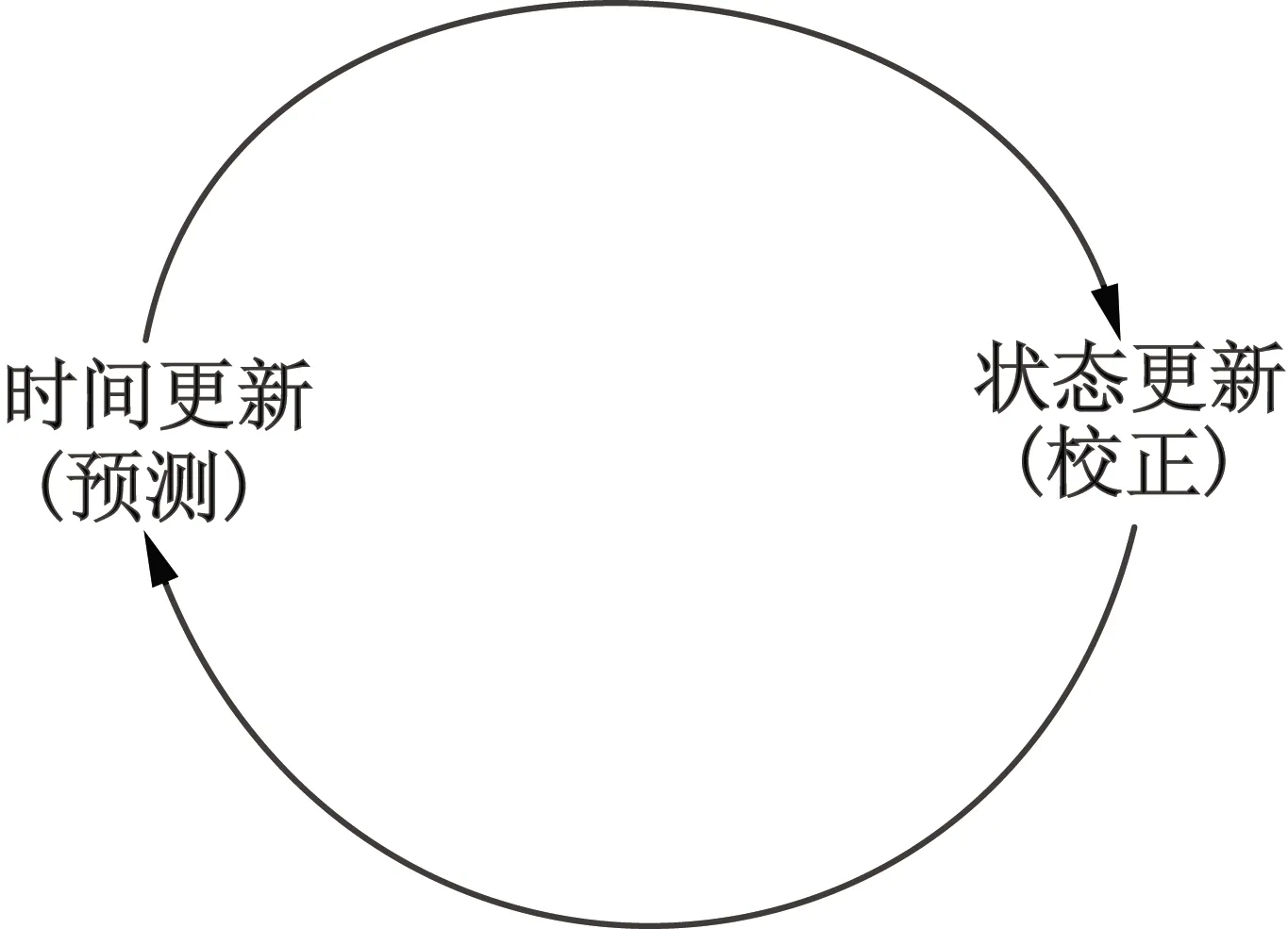
圖6 卡爾曼濾波器遞推原理圖

圖6中，時間更新是利用當前所處時刻的狀態估計和其誒方程估計來更新下一時刻的初步估計值。狀態更新是利用系統中的反饋作用通過時間更新中的初步估計值計算出最終估計值。

在實際生活中我們所遇到的都是非線性系統，但是卡爾曼濾波器算法主要針對線性系統，所以必須要對非線性系統進行線性化處理，線性化之后再采用卡爾曼濾波器，得到擴展卡爾曼濾波器。但是，我們遇到的非線性系統并不一定都可以進行合理的線性化變換，需要假設在所處理的非線性系統中，經過合理的線性變換后依舊可以如實反映系統的各種性質，并且可以解出所建立的非線性微分方程。

在非線性系統中設系統狀態變量為x(t)，系統輸出變量為y(t)，則有：

(15)

式中：u(t)為輸入矢量;σ(t)和μ(t)分別為相互獨立且具有零均值高斯白噪聲特性的系統噪聲和測量噪聲，其中σ(t)的協方差為Q(t)，μ(t)的協方差為R(t)。

定義Jacobian矩陣：

(16)

(17)

利用Jacobian矩陣對式(15)進行線性化處理，離散化后可得：

Δx(k)=Φ[tk,tk-1,x(k-1)]Δx(tk-1)+σ(tk-1)

(18)

開始時間需要知道系統最初值，但在一個隨機的實際系統中這一點是無法辦到的，在最初估計中誤差會較大，隨著時間的推移，在一致隨機可控和可觀測系統中，會慢慢收斂直到系統變得穩定。由上文提到的設計原理，設計的卡爾曼濾波器狀態方程：

(19)

(20)

(21)

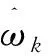
(22)

改進后的結構圖如圖7所示。

圖7 改進后的滑模觀測器結構圖

整體優化后基于滑模觀測器的PMSM轉子位置檢測體統結構圖如圖8所示。

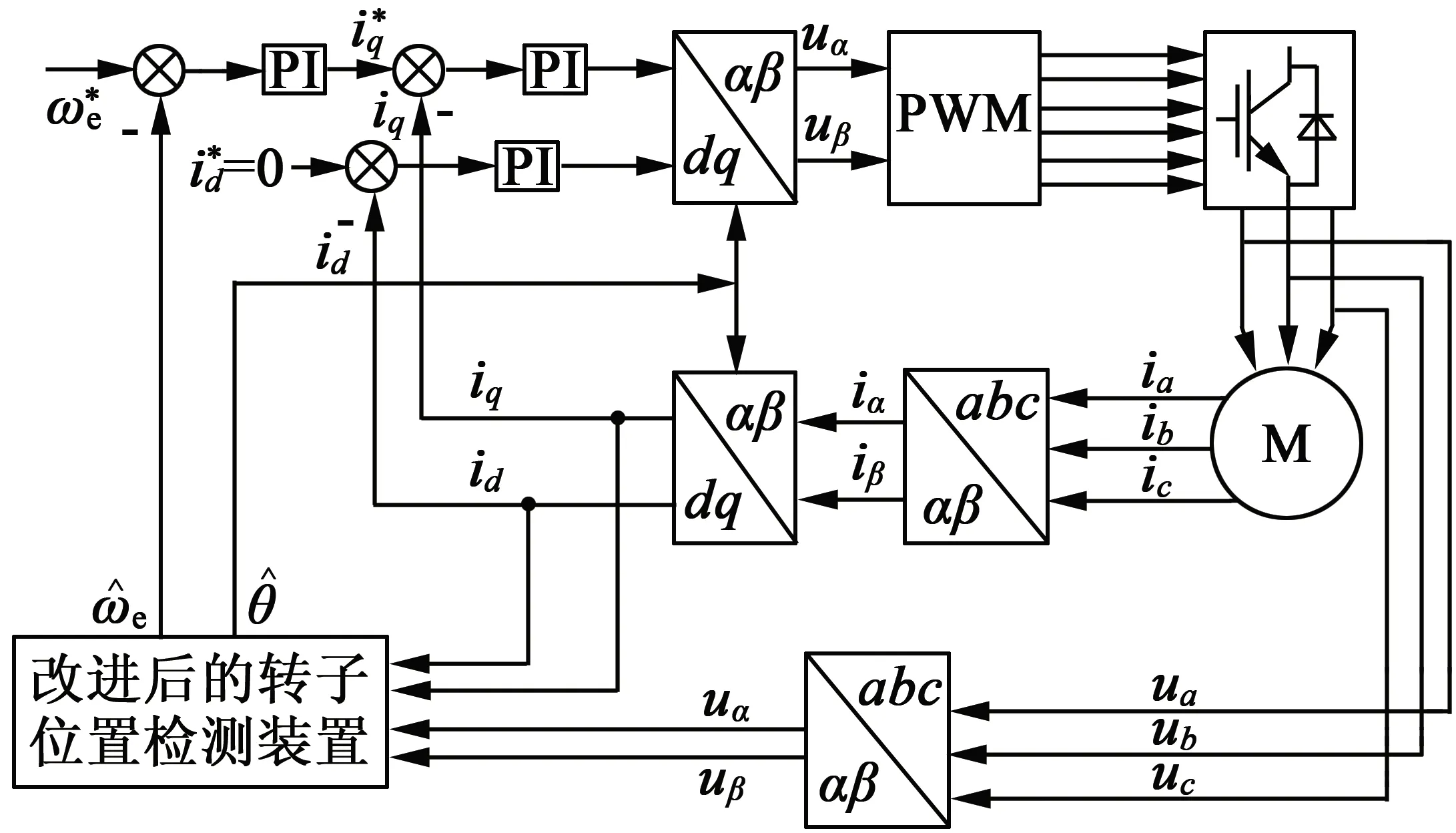
圖8 含卡爾曼濾波環節的系統結構圖

4 改進后的仿真結果分析

為了驗證上述的改進方法，設計了仿真建模，其中電機動態參數如下：額定功率P=1.25 kW，額定電壓U=230 V，極對數p=4，d，q軸電感Ld=Lq=3.13 mH,轉動慣量J=0.008 kg·m2。

電機空載起動，初始速度給定為1 200 r/min，在0.2 s時給電機突加負載10 N·m，待轉速穩定之后，在0.4 s給電機減負載5 N·m，如圖9～圖11所示，檢測對比傳統方法和優化后的滑模觀測器對電機轉子位置和轉速的估測跟蹤性能。

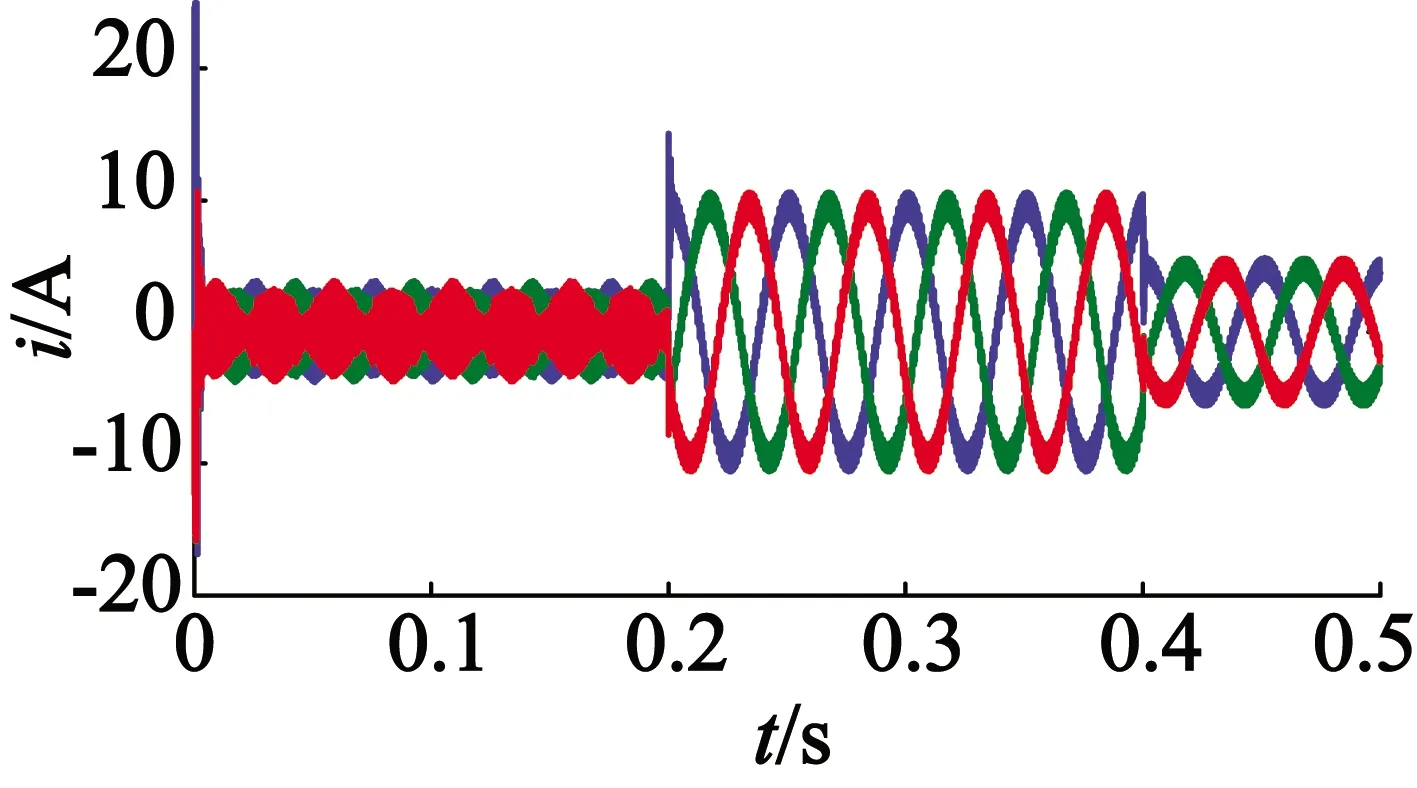
圖9 加減負載電機定子電流圖

優化前后滑模觀測器轉速和角度對比如圖10所示。傳統的滑模觀測器在0.05 s時系統才進入了穩定狀態，但是優化后的滑模觀測器在0.03 s就很快跟蹤到了系統速度，在增加電機負載和減少電機負載的情況下，優化后的滑模觀測器觀測曲線都要比傳統的滑模觀測器觀測曲線波動都要小，且率先進入系統穩定階段。優化后的滑模觀測器電機轉子位置誤差始終保持在0.05 rad范圍以內。優化后的滑模觀測器系統在空載起動和加減負載情況下跟蹤情況波動小，超調量小，電機的響應速度提高，性能明顯得到了提升。

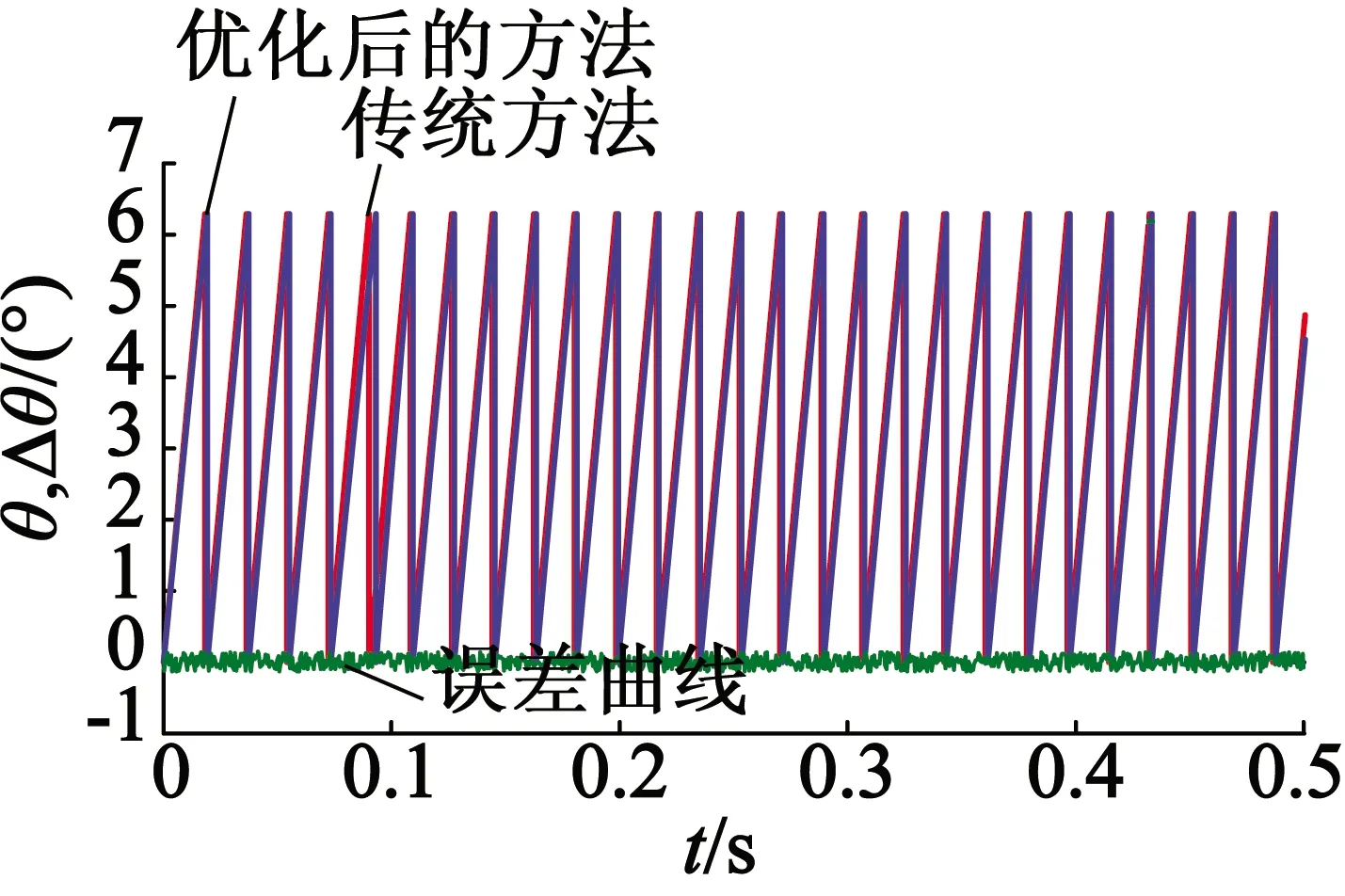
(b) 轉子角度

給定電機初始轉速為1 200 r/min，在0.2 s之后轉速突變為900 r/min，在此過程中傳統的滑模觀測器和改進后的滑模觀測器對電機的轉速和轉子角度估測情況如圖11所示。

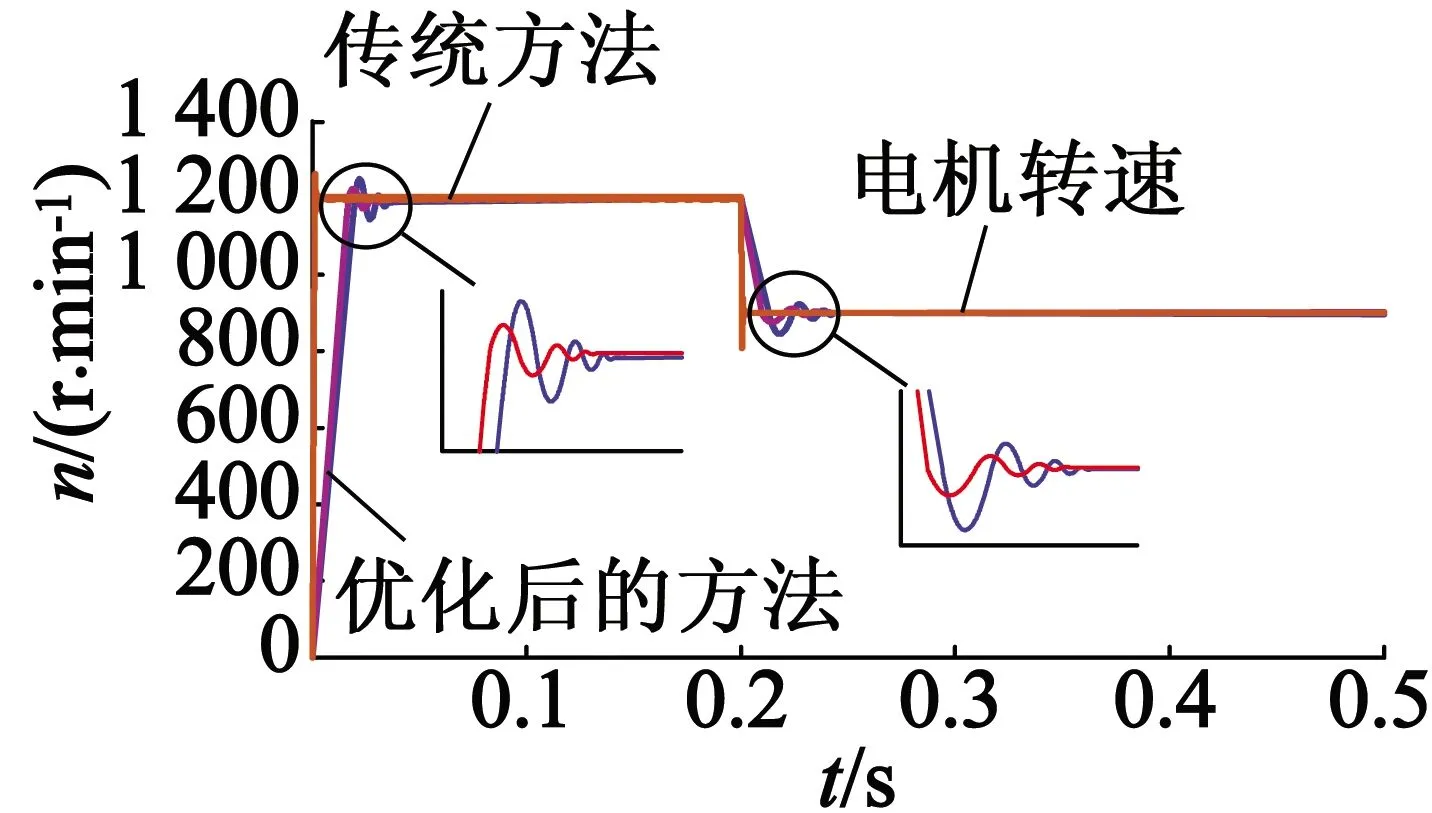
(a) 轉速

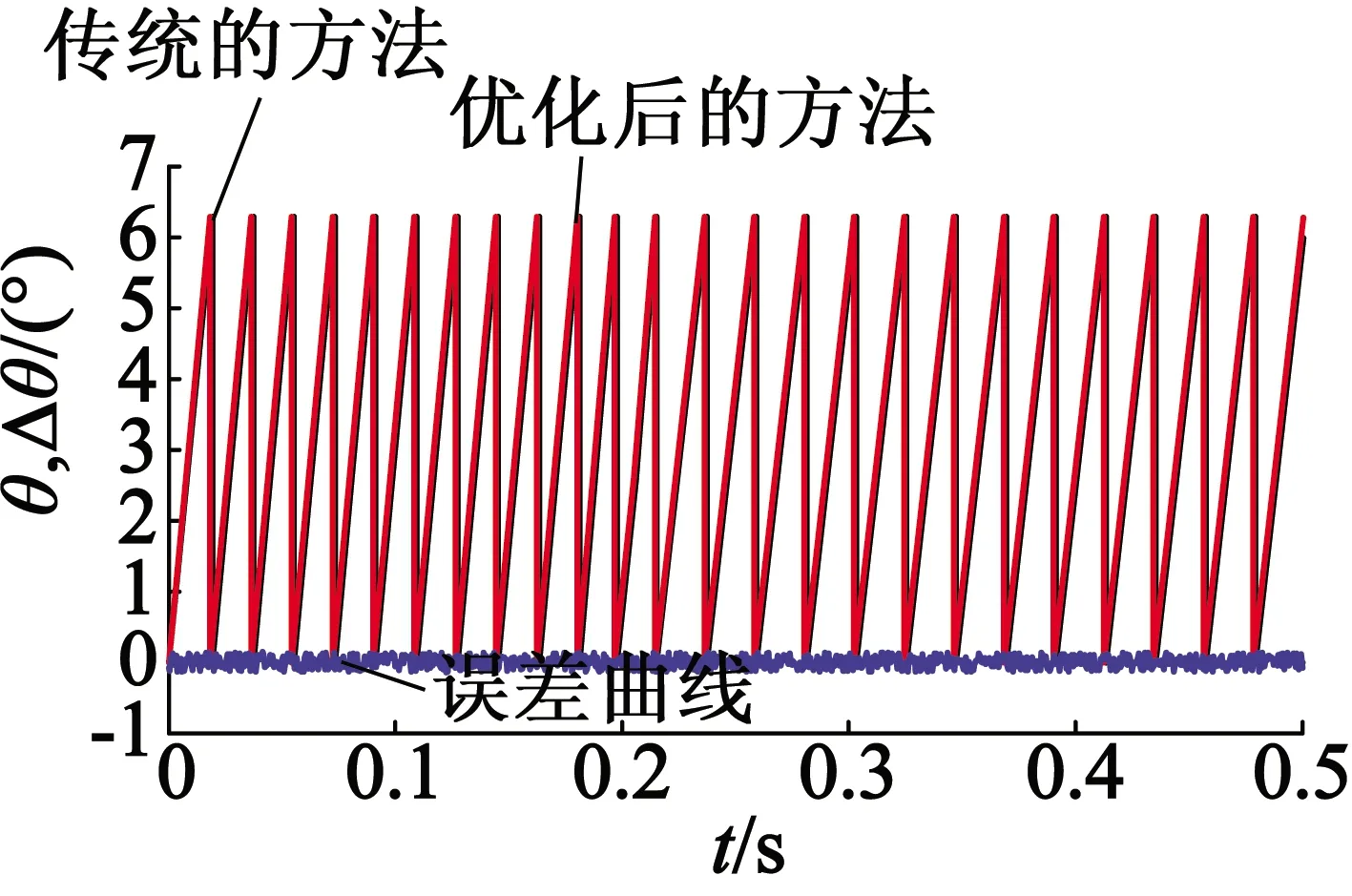
(b) 轉子角度

由圖11中可知，在電機起動和減速階段，優化后的滑模觀測器曲線都要比傳統滑模觀測測器曲線波動小，并且角度誤差都在0.03 rad以內，在減速過程中轉速曲線變化平緩，電機反應速度快，運行穩定，超調量小，動態靜態性能都得到提升。

5 結 語

本文主要研究無位置傳感器PMSM轉子位置及速度檢測，基于傳統滑模觀測器，對傳統滑模變結構的開關函數進行改進；傳統滑模觀測器中的低通濾波器不能有效濾除諧波，影響電機運行性能，因此引入了擴展卡爾曼濾波器，高效濾除高頻紋波，提高系統動態響應。最后在MATLAB/Simulink平臺進行仿真建模研究，對仿真結果進行分析后有如下結論：改進后的方法對于硬件成本要求較低，系統的結構簡單，超調量小，優化后性能有所提升；在電機負載和轉速改變時，與傳統方法相比，該方法誤差變小，動態性能變好，對電機的轉速和位置有更好的估測效果。