學術評價中指標無量綱法對VIKOR評價的影響研究

摘 要：[目的/意義]VIKOR評價法是一種重要的非線性多屬性評價方法，在學術評價中得到了廣泛的應用，但是對于無量綱方法對VIKOR評價結果的影響研究卻比較缺乏，實際應用中比較隨意。[方法/過程]本文首先建立無量綱方法對VIKOR評價方法影響的分析框架，分析了無量綱方法對VIKOR評價的影響機制，然后基于JCR2017經濟學期刊的數據進行了實證。[結果/結論]無量綱方法對VIKOR評價的影響機制包括評價值排序、統計特征與模擬權重3個方面;指標無量綱方法同樣會影響VIKOR評價方法的模擬權重;極大值無量綱VIKOR評價結果總體優于極差無量綱;VIKOR評價方法是一種對無量綱方法比較敏感的評價方法;當VIKOR用于學術評價時建議首選極大值無量綱方法。

關鍵詞：學術評價;VIKOR;無量綱方法;極大值無量綱;極差無量綱

DOI：10.3969/j.issn.1008-0821.2020.07.013

〔中圖分類號〕G302 〔文獻標識碼〕A 〔文章編號〕1008-0821（2020）07-0126-08

Study on the Influence of Index Dimensionless Method on

VIKOR Evaluation in Academic Evaluation

Yu Liping

（School of Statistics and Mathematics，Zhejiang Gongshang University，Hangzhou 310018，China）

Abstract：[Purpose/Significance]VIKOR evaluation method is an important non-linear multi-attribute evaluation method，which has been widely used in academic evaluation.However，there is a lack of research on the influence of dimensionless method on VIKOR evaluation results，which is relatively random in practical application.[Method/Process]Firstly，This paper established an analytical framework for the impact of dimensionless method on VIKOR evaluation method，and analysed the impact mechanism of dimensionless method on VIKOR evaluation.Then，an empirical study was carried out based on the data of JCR2017 Economics Journal.[Result/Conclusion]The results showed that the influence mechanism of the dimensionless method on VIKOR evaluation included three aspects：ranking of evaluation values，statistical characteristics and simulation weight;The dimensionless method also affected the simulation weight of the VIKOR evaluation method;The result of maximum dimensionless VIKOR evaluation was generally superior to range dimensionless;VIKOR evaluation method was sensitive to the dimensionless method;Maximum dimensionless methods were recommended when VIKOR is used for academic evaluation.

Key words：academic evaluation;VIKOR;dimensionless method;maximum dimensionless;range dimensionless

在學術評價中，多屬性評價方法是一種非常重要的評價手段。所謂多屬性評價方法，就是選取若干評價指標，將其進行無量綱化處理，然后采用某種評價方法進行評價，得到評價結果。多屬性評價通過建立指標體系，從多方位進行學術評價，能夠提供相對全面的信息，再加上評價方法眾多，每種方法均有其一定的適用范圍，可以根據評價需要靈活選取。目前多屬性評價已經在大學評價、學科評價、科研人員評價、科技機構評價、學術期刊評價、圖書館評價等得到了廣泛的應用。

多準則妥協解排序法（VIKOR）是一個針對復雜系統的多屬性評價方法。該方法由Opricovic S[1]最早提出，其最大的特點是根據最大的“群體效用”和最小化的“個體遺憾”來進行評價。在評價中，所謂群體效用，就是對于某評價對象而言，各評價指標的離理想解的距離之和，越小越好;所謂個體遺憾，就是某評價對象到理想解的最大距離，當然也是越小越好（Opricovic S等）[2]。VIKOR對評價的要求就是要兼顧這兩方面，好的方面越來越好，差的方面也不能太差。在學術評價中，一方面需要提高各正向指標的值，保證指標總和要大;另一方面需要兼顧木桶理論，最差的指標也不能太差，因此VIKOR評價應用日趨廣泛。

評價指標的無量綱化處理，或者說評價指標的標準化方法會影響包括VIKOR評價方法在內的所有多屬性評價方法。常見的指標無量綱化處理方法包括極大值法、極差法、功效系數法、z值法等等。無量綱方法不同會影響到評價中的數據處理，進而對評價結果產生影響，對于VIKOR評價法而言也不例外。由于各種多屬性評價方法原理不同，指標無量綱方法對評價的影響機制也不相同，加上學術評價指標數據許多并不服從正態分布，數據分布偏倚（Vinkler P;Seglen P O）[3-4]，這對評價結果的影響會更大。在指標體系多屬性評價中，評價指標的無量綱方法沒有得到足夠的重視，往往被簡單化對待，無量綱處理在很大程度上改變了評價指標的數據特征，有些統計分析方法對此非常敏感（魏登云）[5]。

研究無量綱方法對于VIKOR評價法的影響機制，不僅有利于加深對VIKOR評價法的理解，有助于指標無量綱方法以及多屬性評價方法的選取，從而豐富多屬性評價理論，而且對于提高學術評價的公信力，促進評價的公開、公平、公正，從評價方法層面保證學術評價的公平，具有十分重要的研究價值。

1 文獻綜述

關于VIKOR評價方法在學術評價中應用，方曦等[6]采用熵權法設置權重，基于VIKOR法對決策情報進行評價。郭強華等[7]基于直線距離改進了VIKOR評價方法，對JCR2015數學期刊進行評價，發現改進VIKOR方法提高了評價效果。劉天卓等[8]提出基于組合賦權和VIKOR的學術期刊綜合評價模型。周慧妮等[9]基于前景理論和VIKOR方法進行競爭情報渠道評價。

關于VIKOR評價方法在企業創新領域的應用，葉玲等[10]根據系統論構建建筑企業技術創新能力評價指標體系，采用BP神經網絡結合VIKOR法進行評價。畢克新[11]等采用VIKOR法對科技型中小企業自主創新能力進行綜合評價。曹霞等[12]運用QFD質量屋模型選擇關鍵指標，結合具有模糊特性的Vague值改進VIKOR法，對企業產學研合作伙伴進行選取。李存斌等[13]構建可能度矩陣，通過VIKOR方法對企業科技發展水平進行評價。張瑞等[14]從技術水平、成果性質、經濟效益、社會效益4個方面建立指標體系，基于VIKOR法建立企業科技成果選擇決策模型。尹夏楠等[15]從創新能力、財務管控和風險控制3個視角構建了高新技術企業成長性評價指標體系，基于VIKOR對中關村IT行業上市公司成長性進行評價。

關于評價指標無量綱方法的作用和地位，Gregory A J等[16]指出在多指標綜合評價的過程中，必須對被評價對象原始指標數據作無量綱化處理，才能消除各個指標的單位和量級等不同而產生的不利影響。Radicchi F等[17]認為在學術評價中，效果理想的學科標準化方法應使得不同學科引文分布大致相同。張立軍等[18]認為選擇合適的指標標準化方法，能夠有效提高綜合評價結果的準確性。張衛華等[19]提出無量綱化方法的合理性取決于評價結果排序的合理性，這是無量綱方法選取的重要標準。劉學之等[20]發現線性變換無量綱方法在處理非均勻分布的指標數據集合時，尤其是對局部集中分布數據的處理存在一定局限性，無法有效地將數據分層，缺乏辨識性，提出采用Logistic曲線進行非線性數據的標準化。張志輝等[21]在大學評價中，發現基于加權優化模型的線性標準化方法比傳統標準化方法效果好。

關于無量綱方法對評價結果的影響，研究角度首先從評價結果展開，Zhang L J等[22]分析了無量綱化方法對綜合評價結果影響的魯棒性，這是一種新的靈敏度分析視角。胡永宏[23]研究發現，若不具備變異信息不變性，則無量綱化處理前后的數據將具有不同的密集程度，必然影響綜合評價結果。張月等[24]在用灰色關聯分析第三產業與GDP關系中，發現比重法與極值法兩種無量綱方法的結果是自相矛盾的。韓明彩[25]認為線性標準化方法難以反映認知標準，此外標準化方法不同計算結果也不同。俞立平等[26]在學術期刊評價中提出一種新的線性反向指標標準化方法，發現這種方法與傳統經典方法相比，評價結果的排序后有所差異。樊紅艷等[27]認為，原始數據無量綱化方法不同所得的排序結果也就明顯不同。

關于無量綱方法對權重的影響，俞立平[28]指出由于無量綱法使得評價指標均值不相等，加上學術評價指標不服從正態分布，必然隱含的自然權重問題，會造成評價實際權重的嚴重扭曲。朱喜安等[29]從權重視角研究了無量綱方法對熵權法評價的影響，并提出極值熵值法。糜萬俊[30]基于離差最大化可能造成權重信息失真的問題，以及約束條件與假設沖突，分析了無量綱化方法對屬性權重影響的傳導機制。江文奇[31]分析了6種不同無量綱化方法對屬性權重影響的敏感性，發現屬性值的無量綱化方法不同，屬性的客觀權重也有所不同，不同的無量綱化方對方案的敏感性和保序性也有差別。王會等[32]分析了線性無量綱化方法對熵值法權重的影響，發現即使具有相同指標值的正指標和逆指標通常會得出不同的權重，任何等差數列數據通過極值法無量綱化后都會得到相同的權重，建議應優先基于原始指標值計算熵權進而進行評價。

從現有的研究看，VIKOR評價方法已經在學術評價與科技評價中得到了廣泛的應用，涉及評價對象包括學術期刊、決策情報、競爭情報、企業創新能力、產學研合作對象選取、企業科技成果等。關于指標無量綱方法的地位與重要性，學術界已經取得共識。關于無量綱對多屬性評價的影響機制，現有的研究集中在其對評價結果以及評價權重的影響，總體上在以.方面有待進一步深入研究：

第一，關于指標無量綱方法對多屬性評價方法的影響機制，尤其是非線性評價方法的影響機制，缺乏系統的分析框架，有必要進一步進行構建研究。

第二，關于指標無量綱方法對VIKOR評價的影響，目前尚缺乏研究。

第三，關于無量綱方法對權重的影響，現有的研究主要集中在客觀賦權上，對于不需要賦權的許多非線性評價方法，并未進行進一步討論，因此無量綱方法對于權重的影響研究遠不充分。

第四，關于指標無量綱方法對評價值的數據分布及其特征影響，現有的研究存在較大不足。

本文以JCR2017經濟學期刊為對象，首先建立指標無量綱方法對非線性評價影響機制的分析框架，然后以VIKOR評價方法為例，選取極大值無量綱、極差無量綱兩種代表性的無量綱方法，全面系統分析指標無量綱方法不同對VIKOR評價的影響，在此基礎上得出結論并進行進一步討論。

2 理論分析

2.1 研究框架

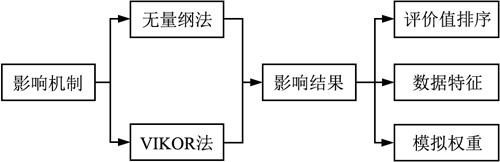
本文的研究框架如圖1所示。首先要研究無量綱方法對于評價的影響機制。影響機制研究必須和評價方法相結合，因為不同的多屬性評價方法原理不同，無量綱方法對其影響效應也不相同。所以無量綱方法、評價方法兩大關鍵要素缺一不可。本文重點研究無量綱方法對VIKOR評價方法的影響機制，顯然不能采用一種無量綱方法，本文以極大值無量綱和極差無量綱兩種最常見的無量綱方法為例，研究其對VIKOR評價方法的影響機制。

圖1 研究框架

關于無量綱方法對評價結果的影響，從3個視角展開，第一是對評價值及其排序的影響;第二是對評價值的數據統計特征與數據分布的影響;第三是對模擬權重的影響。

關于無量綱方法對于模擬權重的影響，有必要進行進一步說明。模擬權重是俞立平[33]提出的，在非線性評價中，雖然可能沒有權重或不需要權重，但是如果用評價結果作為因變量，評價指標作為自變量進行回歸，那么回歸系數代表了各指標的重要性大小，將其進行歸一化處理就是模擬權重。為了減少評價指標間的多重共線性，可以采用偏最小二乘法進行回歸。通過模擬權重分析指標無量綱方法對評價結果的影響是一種方法論上的突破，可以在傳統無量綱方法對權重影響分析的基礎上，分析無量綱方法對所有非線性評價方法的影響。

2.2 VIKOR評價方法的原理

了解VIKOR評價方法的原理是進一步分析無量綱方法對其影響機制的基礎，VIKOR評價的步驟是：

1）對原始評價指標進行無量綱處理，確定每個指標的正理想解f+ij以及負理想解f-ij，即最好的評價對象與最差的評價對象。i為評價對象數量，j為評價指標數量。

2）計算評價對象i的群體效用值S和個體遺憾值R：

Si=∑nj=1ωjf+ij-fijf+ij-f-ij

Ri=maxjωjf+ij-fijf+ij-f-ij（1）

式（1）中，ωj為指標的權重。

3）計算評價對象i的評價結果值Q。

Qi=vSi-S-S+-S-+（1-v）Ri-R-R+-R-（2）

式（2）中，S+=maxSi，S-=minSi ，R+=maxRi，R-=minRi。v表示“群體效用”和“個體遺憾”調節系數，其值介于0～1之間。一般情況.取v=0.5，表示群體效用與個體遺憾同等重要，v越大，說明更關注群體效用，v越小，說明更關注個體遺憾。

4）根據S、R、Q的升序對評價結果進行排序，Q值越小，說明評價對象越優。

5）對妥協解Q進行驗證，其方法是優先對Q進行升序排序，假設A第一，B第二，那么Q滿足以.條件（如果有一個條件不符合，則存在一組妥協解）：

條件1：假設m是評價對象個數，DQ=1/（m-1）。那么Q（B）-Q（A）≥DQ。

條件2：根據S和R值，A也是最優解。

2.3 無量綱方法對于VIKOR評價的影響機制

極大值無量綱方法的計算公式是：

fij=xijmax（xij）（3）

式（3）中，xij表示原始指標數據，這里xij表示正向指標，反向指標的標準化方法原理類似，這里不再贅述。

極差無量綱方法的計算公式是：

fij=xij-min（xij）max（xij）-min（xij）（4）

可以證明，對于同一指標，極大值無量綱值大于極差無量綱值：

xijmax（xij）-xij-min（xij）max（xij）-min（xij）=min（xij）[max（xij）-xij]max（xij）[max（xij）-min（xij）]>0（5）

假設極大值無量綱方法的指標值為fa，極差無量綱方法的指標值為fb，可知fa>fb，對于同一指標同一評價對象，其群體效用分別為：

Sa=1-fa1-min（f）? Sb=1-fb1-0（6）

由于Sa分子小于Sb，并且Sa分母也小于Sb，所以Sa與Sb的大小并不確定，完全取決于數據。

對于個體遺憾值R而言，兩種無量綱方法的極大值大小也不確定，同樣取決于數據。

結論：盡管極大值無量綱結果大于極差無量綱，但由于VIKOR評價方法的群體效用與個體遺憾的大小難以比較，所以無量綱方法對于VIKOR評價的影響機制完全取決于指標數據，沒有規律可循。

3 數據與實證結果

3.1 研究數據

本文采用JCR2017經濟學期刊數據為例來進行分析，選取的評價指標包括三大類9個指標，第一是被引指標，包括：影響因子IF、5年影響因子IF5、他引影響因子IFW、即年指標II、總被引頻次TC;第二是特征因子指標，包括特征因子ES、論文影響分值AIS;第三是時間指標，包括被引半衰期CHL1、引用半衰期CHL2。

JCR2017共有期刊353種，由于部分期刊存在數據缺失，實際選取了321種期刊數據進行分析。

3.2 評價結果值分析

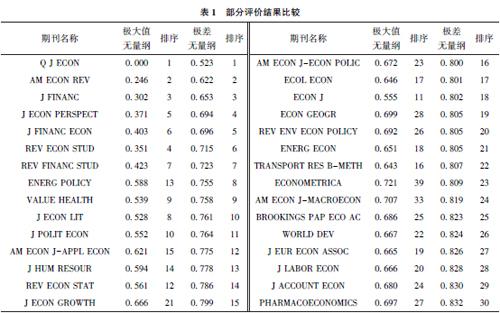
分別采用極大值無量綱方法與極差無量綱方法對評價指標進行處理，然后采用VIKOR評價方法進行評價，結果如表1所示。由于篇幅限制，本文僅公布極差無量綱方法VIKOR評價的前30種期刊的評價結果。

從評價結果看，盡管優秀期刊的區分度相對一般期刊的區分度要大，但兩種無量綱方法對評價結果的影響還是較大的，前30種期刊中排序一致的期刊只有7種。當然無量綱方法不同是問題的一個方面，另一個重要原因是學術期刊指標數據分布往往是偏倚的，對評價結果的影響較大。

3.3 評價值數據統計分析

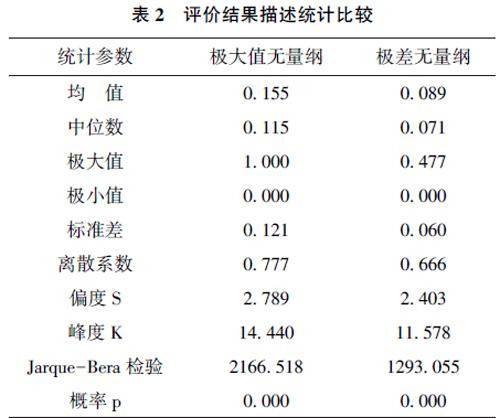
兩種無量綱方法的VIKOR評價結果描述統計如表2所示。由于VIKOR評價方法評價值越小越優，為了符合日常習慣分別用1減去極大值無量綱法與極差無量綱法的評價結果，在此基礎上進行數據統計分析。

從均值看，極大值無量綱VIKOR評價結果大于極差無量綱VIKOR評價結果。極大值無量綱方法評價結果的均值為0.155，極差無量綱方法評價結果的均值為0.089。繼續采用配對樣本t檢驗進

行檢驗。結果t值為18.880，p值為0.000，拒絕均值沒有顯著差異的原假設，也就是說采用極大值無量綱方法有助于提高VIKOR評價方法的均值。由于極大值無量綱方法的指標值大于極差無量綱法，可以進一步推論得到，極大值無量綱方法的指標均值大于極差無量綱法，這樣VIKOR評價結果的均值也較高是正常的。

從離散系數看，極大值無量綱VIKOR評價值的離散系數為0.121，極差無量綱VIKOR評價值的離散系數為0.060，同樣說明極大值無量綱VIKOR評價值的離散系數要大于極差無量綱法。

從極大值看，極大值無量綱VIKOR評價的極大值為1，極差無量綱VIKOR評價的極大值為0.477，從這個角度，極差無量綱VIKOR評價的打分偏低。

從數據分布看，盡管兩種評價結果均不服從正態分布，但極大值無量綱VIKOR評價結果的Jaque-Bera值更大，更接近正態分布。

3.4 模擬權重比較

由于總被引頻次、影響因子、他引影響因子、5年影響因子等指標之間相關度較高，因此不能采用傳統的回歸方法來估計各評價指標的權重，可以采用偏最小二乘法來進行估計。偏最小二乘法（PLS）由Wold S等[34]提出，將主成分分析、典型相關分析和多元線性回歸相結合，特別適合較少觀測數據或較嚴重多重共線性的分析處理。

極大值無量綱VIKOR評價方差解釋比例如表3所示，當隱含成分為2時，擬合優度從0.921提升至0.933，隨著隱含成分的增加，其擬合優度增加較少，因此全用隱含成分為2的回歸結果，如表4所示。

制動態方程右式均為0，即可得到三維復制動力系統（4）的9個均衡點，包括8個角點E（0∨1，0∨1，0∨1）和1個可能存在的非角點E（x*，y*，z*）。由演化博弈理論和Friedman判定方法可知，系統均衡點為三維復制動力系統演化穩定點的充分必要條件為：將系統平衡點帶入雅克比矩陣后，當且僅當該雅克比矩陣的所有特征值滿足非正條件。

最后計算極大值無量綱VIKOR評價的模擬權重與極差無量綱VIKOR評價的模擬權重，結果如表7所示。

從模擬權重的計算結果看，5年影響因子模擬權重最高，極大值無量綱VIKOR評價第二、第三模擬權重指標分別為他引影響因子、影響因子，而極差無量綱VIKOR評價第二、第三模擬權重分別lang=EN-US>0∨1，0∨1，0∨1）和1個可能存在的非角點E（x*，y*，z*）。由演化博弈理論和Friedman判定方法可知，系統均衡點為三維復制動力系統演化穩定點的充分必要條件為：將系統平衡點帶入雅克比矩陣后，當且僅當該雅克比矩陣的所有特征值滿足非正條件。

為影響因子、他引影響因子，兩種無量綱法VIKOR評價結果的第二、第三高模擬權重位置發生顛倒，其他指標的模擬權重排序不變，也就是說，由于無量綱法不同，導致VIKOR評價的指標模擬權重不同，并且大小排序有一些變化。

4 結論與討論

4.1 無量綱方法對VIKOR評價的影響機制包括評價值排序、統計特征與模擬權重

本文從理論上分析了評價指標無量綱方法對VIKOR評價的影響機制，認為其包括3個方面，第一是無量綱方法會影響VIKOR的評價值以及結果排序，基于JCR2017經濟學期刊的實證研究表明，分別采用極大值無量綱法與極差無量綱法的評價結果及排序相差較大。第二是無量綱方法會影響評價值的數據統計特征與數據分布。第三是對評價指標模擬權重的影響。從影響效應看，對評價結果排序的影響最大，而對統計特征與數據分布及模擬權重的影響是隱含的，往往得不到應有的重視。

4.2 指標無量綱方法同樣會影響VIKOR評價方法的模擬權重

本文的實證研究結果表明，由于指標無量綱方法不同，導致VIKOR評價的指標模擬權重也會發生一些變化，一方面是指標模擬權重大小的排序會發生變化，另一方面是指標模擬權重本身大小也會發生變化。這個結論與現有研究認為指標無量綱方法不同會影響客觀權重類似。

4.3 極大值無量綱法VIKOR評價結果總體優于極差無量綱法

實證研究表明，極大值無量綱法VIKOR評價結果的均值要大于極差無量綱法，并且極大值無量綱法VIKOR評價離散系數也大于極差無量綱法，擁有更好的區分度。此外極大值無量綱法VIKOR評價結果的正向極大值為1，而極差無量綱法VIKOR評價結果的正向極大值較小，不符合實際習慣，總體上極大值無量綱VIKOR評價的效果要優于極差無量綱VIKOR評價。

4.4 當VIKOR用于學術評價時建議首選極大值無量綱方法

極大值無量綱方法與極差無量綱方法作為兩種主流的、應用最為廣泛的無量綱方法，在學術評價與科技評價中得到了廣泛的應用。在選取評價方法時，實踐中隨意性很強，對于有些評價方法也許不敏感，但是VIKOR評價方法是一種對無量綱方法比較敏感的評價方法。在學術評價與科技評價中，由于數據分布往往不服從正態分布，數據分布偏倚，導致不同無量綱方法的VIKOR評價結果排序相差較大，在這種情況.，建議優選極大值標準化方法。

本文拓展了從模擬權重以及評價結果數據特征角度分析指標無量綱法對多屬性評價影響的視角，并且開拓了無量綱方法對VIKOR評價影響機制的研究。在研究方法上，采用偏最小二乘法代替多元回歸，大大降低了評價指標之間的多重共線性，使得模擬權重的估計更加準確。

本文的研究框架也適用于研究無量綱方法對其他非線性多屬性評價方法的影響，當然由于本文無法對無量綱方法對VIKOR評價方法的影響進行證明，具體研究結論尚需進一步檢驗。此外由于無量綱化方法眾多，本文僅僅采用兩種常見的無量綱法進行比較分析，至于其他無量綱法對VIKOR的影響有待進一步研究。

參考文獻

[1]Opricovic S.Multi Criteria Optimization of Civil Engineering Systems[D].Belgrade：Faculty of Civil Engineering，1998.

[2]Opricovic S，Tzeng G H.Extended VIKOR Method in Comparison with Outranking Methods[J].European Journal of Operational Research，2007，178（2）：514-529.

[3]Vinkler P.Introducing the Current Contribution Index for Characterizing the Recent，Relevant Impact of Journals[J].Scientometrics，2008，79（2）：409-420.

[4]Seglen P O.The Skewness of Science[J].Journal of the American Society for Information Science，1992，43（9）：628-638.

[5]魏登云.數據的標準化處理在體育綜合評價中的應用辨析[J].上海體育學院學報，2016，40（4）：21-26.

[6]方曦，李治東，熊焰，等.基于模糊VIKOR法的企業決策情報評價及應用[J].情報理論與實踐，2015，38（3）：49-52，44.

[7]郭強華，羅鋒，俞立平.基于改進的VIKOR科技評價方法研究——直線距離因子多準則妥協解法LDF-VIKOR[J].情報雜志，2018，37（4）：171-175.

[8]劉天卓，余穎.基于組合賦權和VIKOR的學術期刊綜合評價研究[J].數學的實踐與認識，2019，49（1）：311-320.

[9]周慧妮，江文奇.基于前景理論和VIKOR的營銷競爭情報評價研究[J].情報雜志，2015，34（10）：16-21.

[10]葉玲，葉貴，付媛.基于BP-VIKOR的建筑企業技術創新評價模型[J].建筑經濟，2018，39（9）：116-120.

[11]畢克新，王筱，高巍.基于VIKOR法的科技型中小企業自主創新能力評價研究[J].科技進步與對策，2011，28（1）：113-119.

[12]曹霞，宋琪.基于企業QFD和改進VIKOR法的產學研合作伙伴選擇研究[J].科技管理研究，2016，36（8）：91-97.

[13]李存斌，張磊，馬原.基于云模型和VIKOR擴展方法的電網企業科技發展區間值多屬性群決策[J].運籌與管理，2018，27（10）：63-69.

[14]張瑞，丁日佳，郝素利.可轉化為國際標準的科技成果選擇決策研究——基于VIKOR法[J].科技進步與對策，2015，32（10）：5-8.

[15]尹夏楠，朱蓮美，鮑新中.基于VIKOR方法的高新技術企業成長性評價[J].財會通訊，2015，（34）：38-41，4.

[16]Gregory A J，Jackson M C.Evaluation Methodologies：A System of Use[J].Journal of Operational Research，1992，43（1）：19-28

[17]Radicchi F，Castellano C.Rescaling Citations of Publications in Physics[J].Physical Review E Statistical Nonlinear & Soft Matter Physics，2011，83（2）：046116.

[18]張立軍，袁能文.線性綜合評價模型中指標標準化方法的比較與選擇[J].統計與信息論壇，2010，25（8）：10-15.

[19]張衛華，趙銘軍.指標無量綱化方法對綜合評價結果可靠性的影響及其實證分析[J].統與信息論壇，2005，（5）：33-36.

[20]劉學之，楊澤宇，沈鳳武，等.基于S型曲線的指標非線性標準化研究[J].統計與信息論壇，2018，33（2）：17-21.

[21]張志輝，程瑩，劉念才.線性學科標準化方法的效果優化及其對科研評價結果的影響——以39所“985工程”大學論文質量排名為例[J].情報學報，2015，34（3）：300-312.

[22]Zhang Lijun，Tao Lu.A Research on Methods of Robust Measurement of Multi-index Comprehensive Evaluation Model[J].Statistics & Information Forum，2011，26（5）：16-20.

[23]胡永宏.對統計綜合評價中幾個問題的認識與探討[J].統計研究，2012，（1）：26-30.

[24]張月，肖峰.GRA方法中的無量綱化比較[J].統計與決策，2005，（4）：120-121.

[25]韓明彩.期刊綜合評價指標標準化方法研究：價值評估法——以圖書情報學期刊為例[J].情報理論與實踐，2012，35（10）：30-32.

[26]俞立平，武夷山.科技評價中標準化方法對評價結果的影響研究[J].現代圖書情報技術，2011，（9）：66-71.

[27]樊紅艷，劉學錄.基于綜合評價法的各種無量綱化方法的比較和優選———以蘭州市永登縣的土地開發為例[J].湖南農業科學，2010，（17）：163-166.

[28]俞立平.線性科技評價中自然權重問題及修正研究——動態最大均值逼近標準化方法[J].統計與信息論壇，2018，33（10）：27-33.

[29]朱喜安，魏國棟.熵值法中無量綱化方法優良標準的探討[J].統計與決策，2015，（2）：12-15.

[30]糜萬俊.無量綱化對屬性權重影響的傳導機制及調權研究[J].統計與決策，2013，（4）：11-14.

[31]江文奇.無量剛化方法對屬性權重影響的敏感性和方案保序性[J].系統工程與電子技術，2012，34（12）：2520-2523.

[32]王會，郭超藝.線性無量綱化方法對熵值法指標權重的影響研究[J].中國人口·資源與環境，2017，27（S2）：95-98.

[33]俞立平.期刊多屬性評價方法篩選研究——指標數據綜合擬合法[J].情報學報，2014，33（3）：296-304.

[34]Wold S，Martens H，Wold H.The Multivariate Calibration Problem in Chemistry Solved By the PLS Method[M].Edited By A Rule and B Kagstron，Springer-Verlag，Heidelberg，1983.

（責任編輯：孫國雷）