連續毫米波雷達測速算法研究

張志鵬　劉慧　朱倩倩　陳春陽　陳兵兵

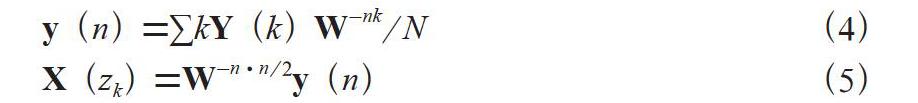
摘? 要：首先圍繞連續毫米波雷達測速算法展開研究，分析了毫米波雷達的測速原理，引出了其測速本質——譜峰搜索;然后利用快速傅里葉變換這一數字信號處理領域中的經典方法，實現了對雷達回波信號的頻譜譜峰位置的快速捕獲;為進一步提高連續毫米波雷達的測速精度，在快速傅里葉變換的基礎上，再引入Chirp Z變換方法，通過頻譜細化實現了對測速算法計算分辨率的有效提升;最后借助MATLAB軟件，完成了對所研算法的程序進行編寫，并設計了若干算例，通過仿真測試驗證了算法的有效性。

關鍵詞：連續毫米波雷達;譜峰搜索;快速傅里葉變換;Chirp Z變換

中圖分類號：TN958? ? ? 文獻標識碼：A 文章編號：2096-4706（2020）02-0053-03

Abstract：Firstly，the algorithm of continuous millimeter wave radar velocity measurement is studied，the principle of velocity measurement is analyzed，and the essence of velocity measurement—spectrum peak search is brought out. Then，the classical method in the field of digital signal processing，fast Fourier transform，is used to capture the spectrum peak position of radar echo signal. In order to further improve the velocity measurement of continuous millimeter wave radar Accuracy，on the basis of fast Fourier transform，the Chirp Z transform method is introduced，and the resolution of the algorithm is effectively improved through spectrum refinement. Finally，with the help of MATLAB software，the program of the algorithm is completed，and several examples are designed，and the effectiveness of the algorithm is verified by simulation test.

Keywords：continuous millimeter wave radar;spectrum peak search;fast Fourier transform;Chirp Z transform

0? 引? 言

智能交通系統（ITS）是一種大范圍、全方位、實時高效的綜合交通運輸管理系統，由于其可有效利用現有交通設施，保障交通安全、提高運輸效率，正日益受到各國的重視，目前已成為二十一世紀的交通發展方向。在各類現有技術中，雷達[1]憑借其全天候工作的特點，成為ITS系統中監測車流量和車速的最有效的手段之一。其中，目前較有代表性的有美國的Wavetronix雷達、加拿大的RTMS雷達等，它們都屬于連續毫米波雷達。本文主要圍繞連續毫米波雷達的測速算法展開研究。

1? 連續毫米波雷達測速原理

毫米波雷達測速系統主要包括高頻頭、預處理系統、終端系統和紅外啟動器等部件，其工作機制為：首先由振蕩器產生毫米波（頻率f0），經隔離器加至環行器，再由天線定向輻射出去;當電磁波在空間遇到障礙物時發生散射[1]，如目標相對雷達是運動的，則反射回來的電磁波將附加一個與目標運動速度成正比的多普勒頻率（fd），使得回波頻率變為f0+fd;接收天線收到該回波后，將其經環行器加至混頻器，最終在混頻器中與本振信號進行混頻。

假設目標的徑向運動速度為vr，光速為c，則毫米波雷達的本振頻率與回波信號中的多普勒頻率間存在如下關系：

可見，只要能準確獲得fd的值，即可求出目標的運動速度。而fd的信息位于混頻器內的中頻信號中，其對應的正是中頻信號頻譜的峰值頻率，故能否有效捕獲該譜峰頻率即成為毫米波雷達測速成功與否的關鍵。由于當今數字計算機所處理的皆為離散數據，因此必須先對中頻信號進行采樣，才能進一步借助離散傅里葉變換等數字信號處理[2]工具對其進行頻譜分析。

2? 快速傅里葉變換及其在譜峰搜索中的應用

眾所周知，信號在時、頻兩個域中具有“周期←→離散”的對應關系[3]，故有限長序列的頻譜為一周期且連續信號。對于該類型信號，計算機無法直接進行處理，因此需要對頻譜進行采樣，從而獲得在時、頻兩個域中皆為周期且離散的信號，進而通過選取主值序列，構造離散傅里葉變換對。而離散傅里葉變換等效于如下的矩陣-向量積運算：

其中X表示離散頻譜，W為離散傅里葉變換基，x表示時域離散信號，其計算復雜度頗高，如將其直接應用于中頻信號的譜峰搜索，毫米波雷達的測速將徹底喪失實時性，故引入離散傅里葉變換的快速算法——快速傅里葉變換（FFT）。

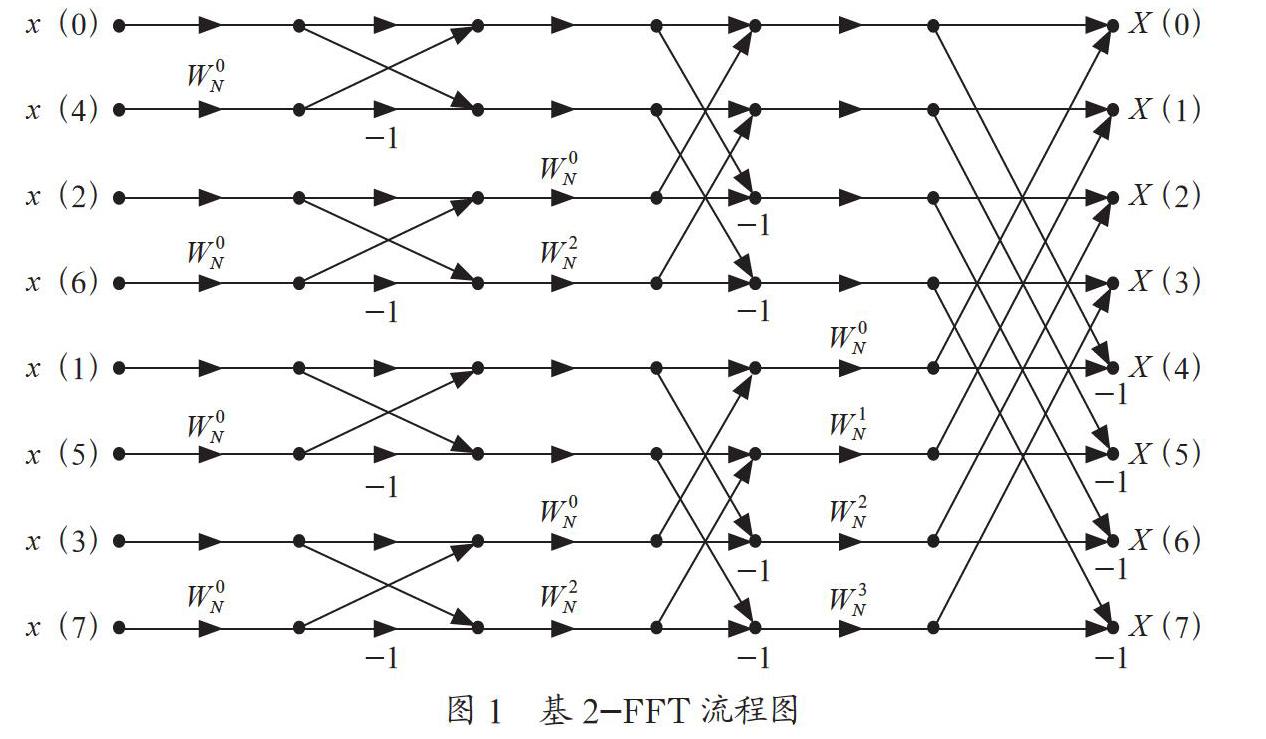
以基2-FFT[2]為例，其算法示意圖如圖1所示。

基2-FFT利用序列兩兩分組、層層分級的思想，實現了對序列的離散傅里葉變換的快速求解，其與直接使用式（3）計算相比，時間復雜度降低了2N/log2N倍。因此，使用快速傅里葉變換，可快速獲取中頻信號的頻譜，從而近乎實時地完成對其譜峰所在頻段的搜索。

然而，由于FFT的本質是離散傅里葉變換，如果譜線之間相隔較大，則不可避免地會丟失中間的部分重要信息，產生所謂的“柵欄效應”。對于譜峰搜索而言，即意味著峰值頻點位置的判定將會出現偏差。因此，在連續毫米波雷達測速系統中，如僅使用快速傅里葉變換對中頻信號進行處理，則系統的測量精度勢必難以保證。一般而言，為削弱柵欄效應，可通過增加信號的采樣點數來縮小譜線間隔，但采樣點數的增加將導致計算量也隨之大幅增加，這又會使得系統的實時性受到極大影響。

3? Chirp Z變換及其在譜峰搜索中的應用

為彌補離散（快速）傅里葉變換在頻譜計算分辨率上的不足，引入Chirp Z變換（CZT）方法[4]，實現對信號頻譜的有效細化，從而最終提高連續毫米波雷達的測速精度。

Chirp Z變換主要是利用傅立葉變換和卷積（圓周卷積）的性質，將z平面的單位圓變成一個螺旋線并逐漸地將單位原點移到單位圓內，這樣信號的頻譜分析即可在z平面的螺旋線上實現（始于任一點，終于另一任意點）。就本質而言，Chirp Z變換并不能減小運算量，但可以計算某個頻段的細化頻譜，因此是建立在采樣點數固定前提下的一種選帶細化手段，尤其適用于單一頻率信號（對應于毫米波雷達的單目標測速）和頻點相距較遠的多頻率信號（多目標測速），可在FFT鎖定譜峰頻段后在指定頻帶內進一步細化搜索峰值頻點。

若速傅里葉變換后所選定的頻帶范圍為Y（k），則CZT主要通過以下兩個公式進行計算：

其中W表示旋轉因子，式（4）的離散傅里葉反變換則可利用圖1所示蝶形運算中的FFT算法進行求解。

從算法原理層面看，CZT實現頻譜細化的過程如下：

（1）將細化頻帶轉換為z平面單位圓圓周上的一段弧，并確定運動軌跡;

（2）計算給定路徑上的CZT;

（3）根據細化頻帶的頻點位置和CZT結果，確定細化頻譜。

在實際工程應用中，Chirp Z變換的主要步驟則為：

（1）確定采樣頻率和對信號的采樣點數，連續采樣若干段;

（2）選取頻譜中的不同頻帶（就連續毫米波雷達測速系統而言，選帶范圍即FFT所確定的譜峰周圍）;

（3）對每個頻帶進行CZT細化，直至其中出現單一頻率成分，否則進一步增大細化倍數;

（4）在指定頻帶上尋找譜峰，獲得較FFT更精確的頻率值、幅值、相位等信息。

本文的算法即是在FFT的基礎上，以其粗略頻譜作為先驗，在指定頻帶內應用CZT對頻譜展開細化，從而在控制運算量的同時，有效提高計算分辨率。

4? 仿真實驗

借助Matlab平臺，對使用發射頻率為24.15 GHz、后端A/D采樣頻率為20.5 kHz的連續毫米波雷達測量速度為1 km/min的單運動目標進行仿真。由式（1）、式（2）可算得，該算例中中頻信號的真實譜峰頻率應為2683.3 Hz。仿真結果如圖2-圖4所示。

由上述結果可見，由于存在柵欄效應，直接應用FFT所得頻譜的峰值頻點為2683 Hz，與真實值存在0.3 Hz的誤差;在進一步運用CZT變換后，峰值頻點計算結果為2683.27 Hz，精度得到了提高。

值得指出的一點是，CZT所提高的為頻譜的計算分辨率，而并非真正意義上的物理分辨率，因此，為進一步提高計算準確性，可適當向后增加采樣點數，即可實現更高精度的測速。

5? 結? 論

本文應用快速傅里葉變換與Chirp Z變換相結合的方法，對連續毫米波雷達后端中頻信號的譜峰信息進行提取，從而實現了毫米波雷達系統對運動目標的快速、準確測速。

參考文獻：

[1] 許小劍，黃培康.雷達系統及其信息處理 [M].北京：電子工業出版社，2010.

[2] 程佩青.數字信號處理教程：第五版 [M].北京：清華大學出版社，2017.

[3] 鄭君里，應啟珩，楊為理.信號與系統（下冊）：第三版 [M].北京：高等教育出版社，2011.

[4] 馬可，張遠安，張開生.CZT和ZFFT頻譜細化性能分析及FPGA實現 [J].計算機測量與控制，2016，24（2）：288-289+303.

作者簡介：張志鵬（1997-），男，漢族，山西晉城人，本科在讀，研究方向：雷達信號處理。