拋體運動分析

孟 勇

(合肥北辰教育培訓學校有限公司，安徽 合肥 230041)

1 引言

拋體運動是指以一定的初速度按照不同的角度將物體拋出，物體僅在重力作用下所做作的運動.針對不同的拋射角度可以將拋體運動分為豎直上拋、豎直下拋、平拋運動與斜拋運動。在日常生活中拋體運動隨處可見，同時在物理教學中它也擔當重要的角色，并且該問題也被相關專業學者不斷地研究。例如在文獻[1]給出了任意時刻拋體運動的曲率半徑的表達式。同時在文獻[2]中將拋體運動規律直接用于指導體育運動，從而提高比賽成績。但是作為自然界真實的拋體運動勢必會受到空氣阻力[3,4]、地球自轉[5]、風等影響，所以為了更加真實而全面的反映出拋體運動的規律，本文從牛頓力學的角度對拋體運動進行詳細的動力學分析。由只受重力下的理想情況下的拋體運動逐步過渡到真實情況中受空氣阻力、科里奧利力、風力下的運動，推導出其在各種情況的運動學方程，從而分析出不同因素對拋體運動產生的影響。

2 只受重力下的拋體運動

針對于圖1 所示，從地面出發并只受重力作用下的拋體，易得到其動力學方程：

圖1 拋體運動

并由其初始條件

可得到其運動學方程為：

從式(4)～(5)可以看出拋體運動在x軸方向上做勻速直線運動的同時，在y軸方向上做勻變速運動.因此拋體運動是一個勻變速曲線運動。此外由式(4)可以得到

然后將上式代入式(5)中可得到拋體運動的軌跡方程

針對上式對θ進行求導并化簡為

然后將上式y'=0 得到

再將式(9)代入式(7)得到拋體運動的包絡線方程

然后再令上式中y=0 和x=0 就分別得到了拋體運動最遠射程與最大射高

這與文獻[6]中所得結果一致。最后根據式(10)～(11)得到包絡線的長度，以及與地面所圍成的面積

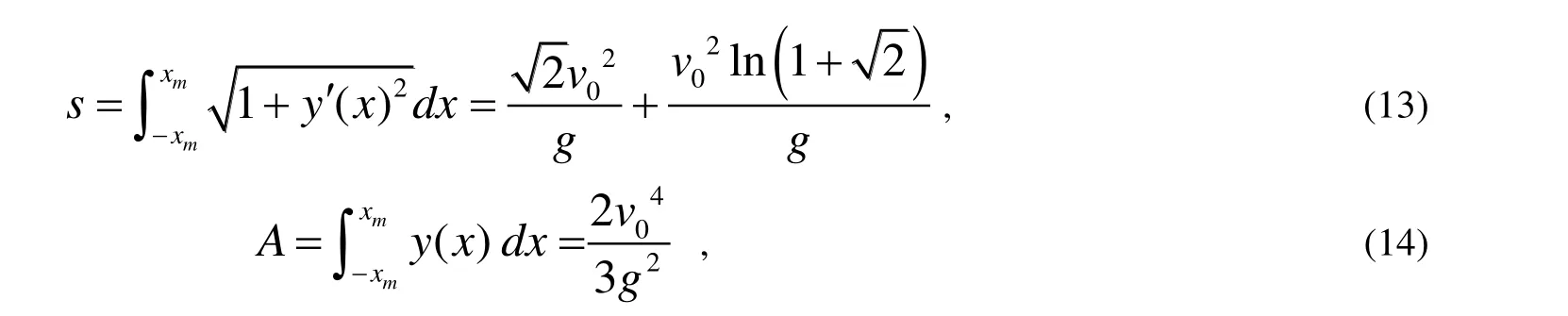
此外為了求拋體運動的軌跡長度與路徑覆蓋面積，先令式(5)中y=0，得到拋體運動的飛行時間為

然后將上式代入式(4)中得到拋體運動的射程表達式

再通過上式與式(7)可得拋體運動的軌跡長度與路徑覆蓋面積為

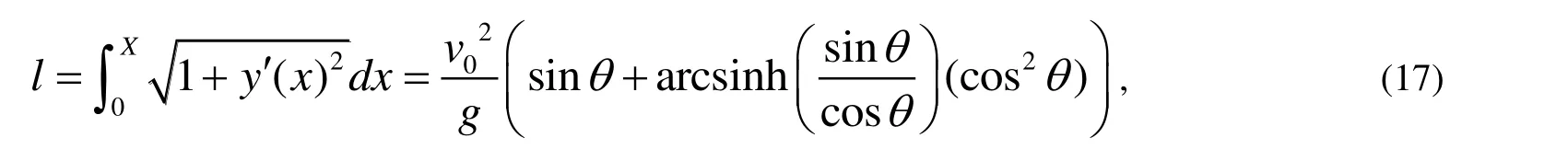
針對于式(17)～(18)可分別對拋射角求導得到軌跡長度與覆蓋面積的最大值，以及相對于的拋射角為

同時設置參數

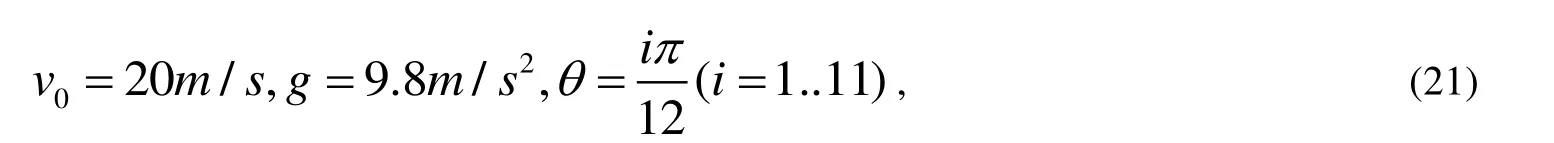
然后根據運動學方程式(4)～(5)以及包絡線方程式(10)，在Maple 軟件平臺[7,8]上制作出如圖2 所示的拋體運動的模擬動畫。

圖2 不同拋射角的拋體運動動畫

從上圖可以看出以相同的速率按照不同拋射角度拋出的小球從同一位置同時拋出，然后在空中散開,共同形成一個以半徑為r=v0t的逐漸變大的圓形,同時這個圓形在y軸方向上做自由落體運動。針對于該現象可以解釋為小球在各個方向上以v=v0勻速運動的同時還在豎直方向參與y=-gt2/2的自由落體運動.然后上述兩種分運動相互獨立又結合在一起，就形成了上述運動。并且還注意到在任何時候所有小球都在包絡線下的粉紅色區域內運動，這驗證了上述求得的包絡線方程的正確性。因此通過以上論述也說明了模擬動畫的制作可以直觀、準確的、全面的反映出拋體運動的規律，達到可視化教學的目的。

3 考慮空氣阻力的拋體運動

物體在空氣中運動總是會受到與速度成正相關的空氣阻力的影響，因此可以設空氣阻力的表達式

其中F(v) 雖然不易得出，需要通過實驗來確定。但在考慮拋體速率較低時可將空氣阻力的大小近似為與速率成正比，即斯托克斯摩擦[9]：

于是在二維空間受到空氣阻力下的拋體運動學方程可寫為：

為了下文討論方便，設β=mγ，則式(24)～(25)可改寫為：

然后將初始條件設置與式(3)相同，則通過求解式(26)～(27)得到受阻力的拋體運動的運動學方程為：

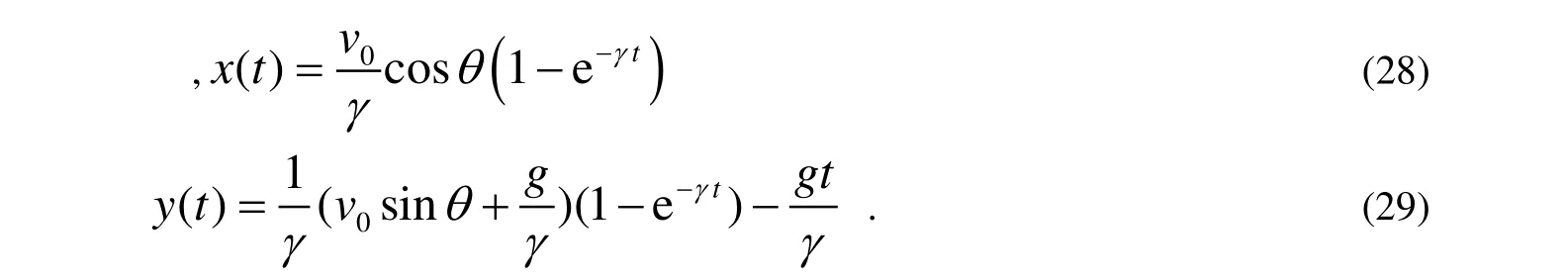
針對于式(29)中令y(t)=0 。可通過數值求解這個超越方程得到拋體運動的總時間。此外，再對式(28)～(29)中時間t求導得到拋體運動的速度表達式

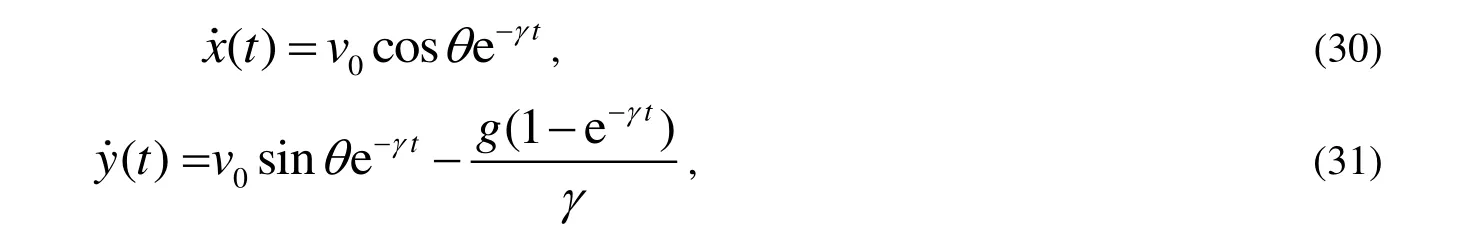
從式(30)～(31)可得拋體運動的收尾速度為

并且由式(29)和式(30)～(31)可得拋體在任意時刻的動能以及該時刻之前因為空氣阻力而損失的機械能

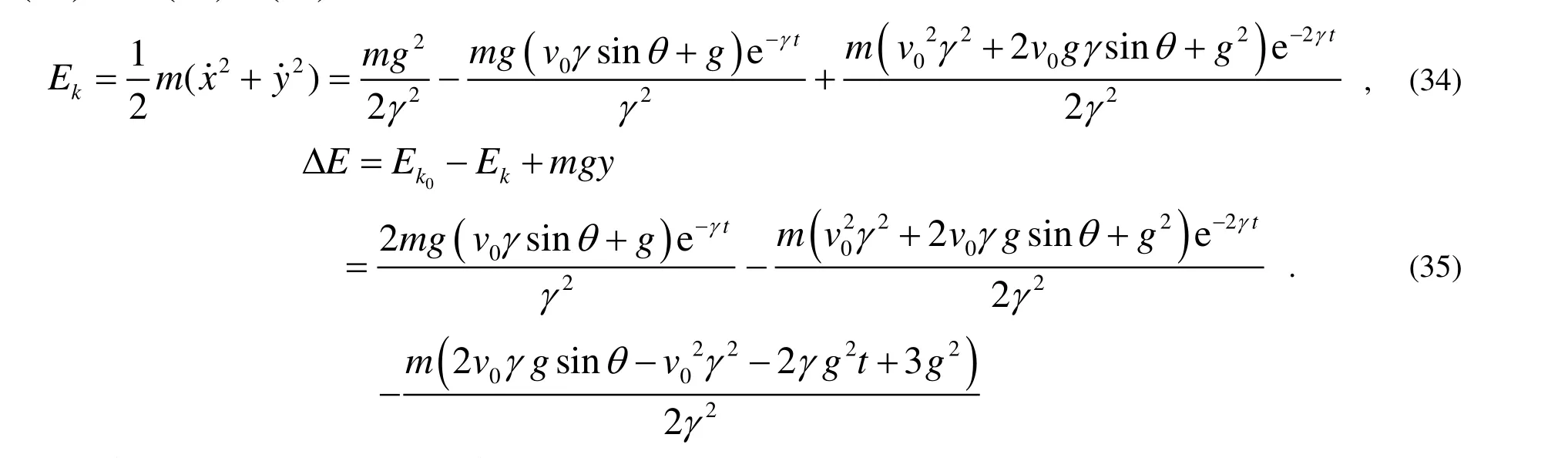
此外,令式(31)等于零，解得拋體運動最高點時間為

再將上式代入式(29)得拋體運動的射高為：

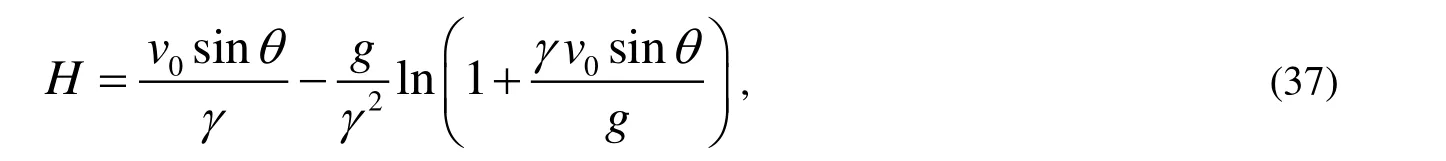
同時由式(28)～(29)可到其軌跡方程：

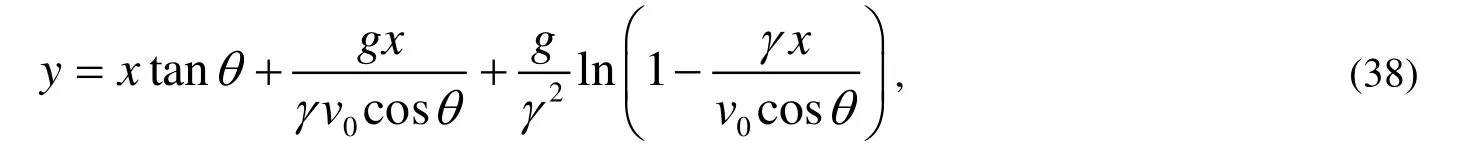
然后設置參數

考察γ值對拋體運動的影響，如圖3 所示：

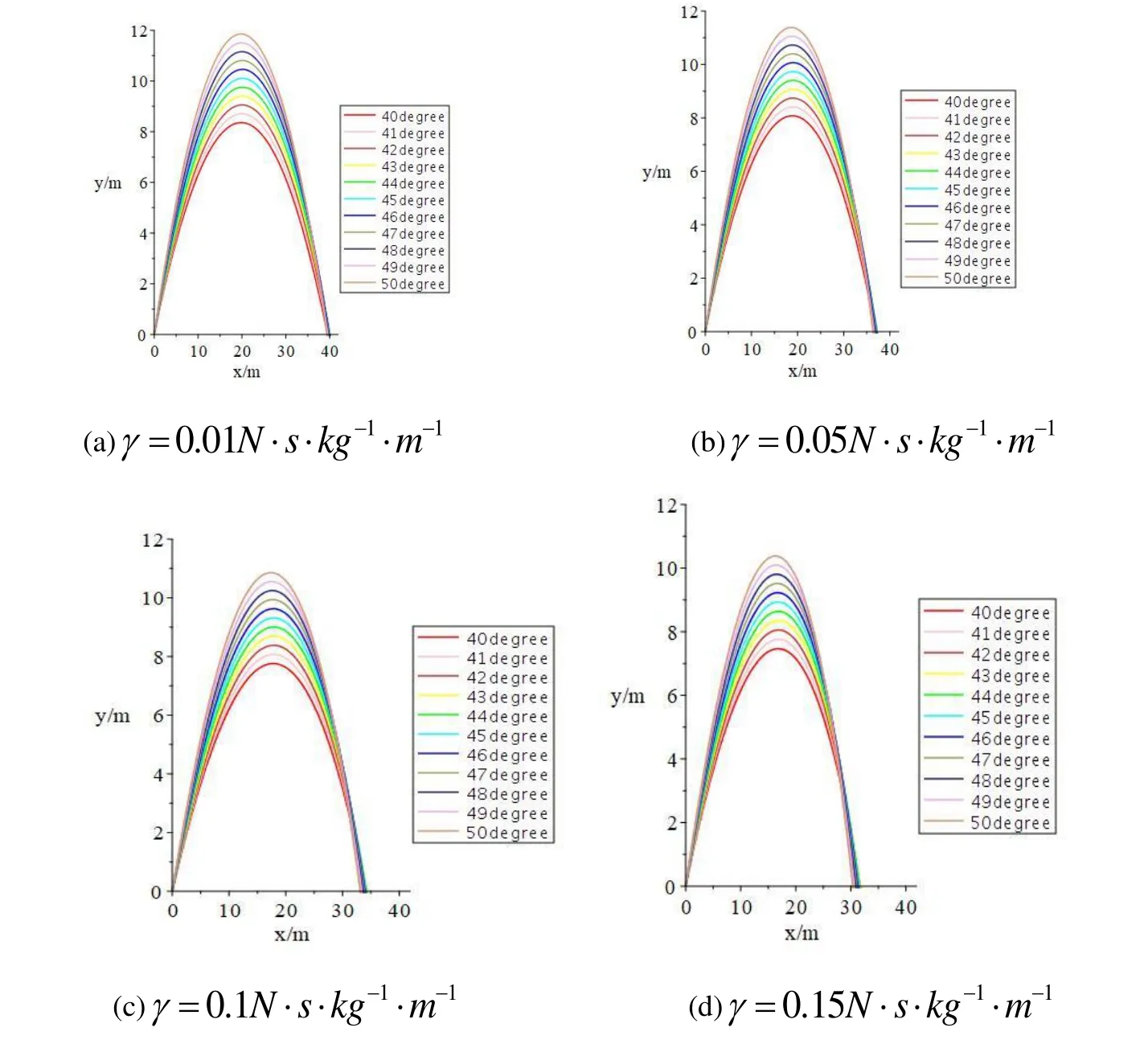
圖3 不同γ 對拋體運動的影響

從圖3 可以看出隨著空氣阻力的增大，拋體運動的射程和射高都逐漸變短了，并且也能觀察到當初速度相同時拋射角越大，射高越大.同時還可以發現隨著γ的增大，拋體運動軌跡圖形的軸對稱性逐漸降低，左邊寬右邊窄。這是因為隨著運動的進行，其水平速度逐漸減小，而在上升過程中拋體的豎直速度逐漸減小，所以上升階段的合速度方向逐漸沿x方向。相反，在下降階段豎直速度逐漸變大，所以合速度方向逐漸偏向-y軸。因此上升過程比下降過程更“寬”。

4 在地球自轉影響下的拋體運動

由于地球是一個非慣性參考系（如圖4），所以在真實情況中考慮地球自轉，所以拋體在運動過程中除了受到重力和空氣阻力外，還要受到科里奧利力這種慣性力的作用，因此根據文獻[10]可以列出三維情況下的動力學方程：

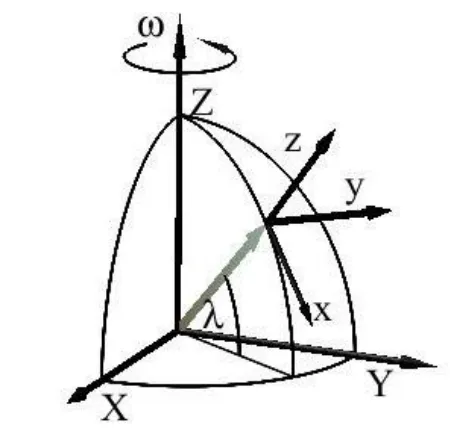
圖4 地球自轉(緯度為λ)

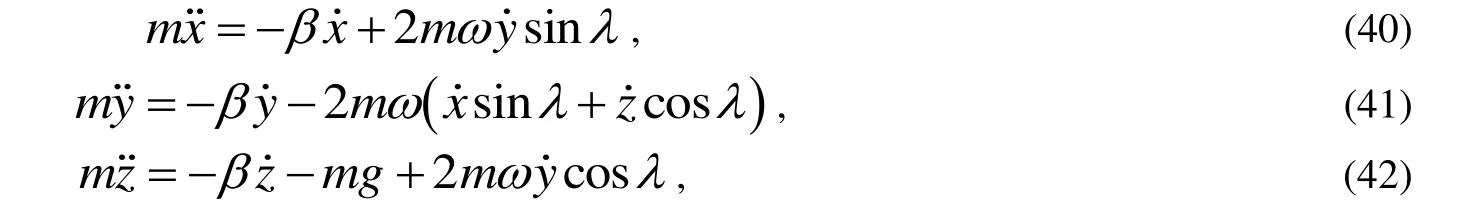
與上文相同令β=mγ，則式(40)～(42)可改寫為：

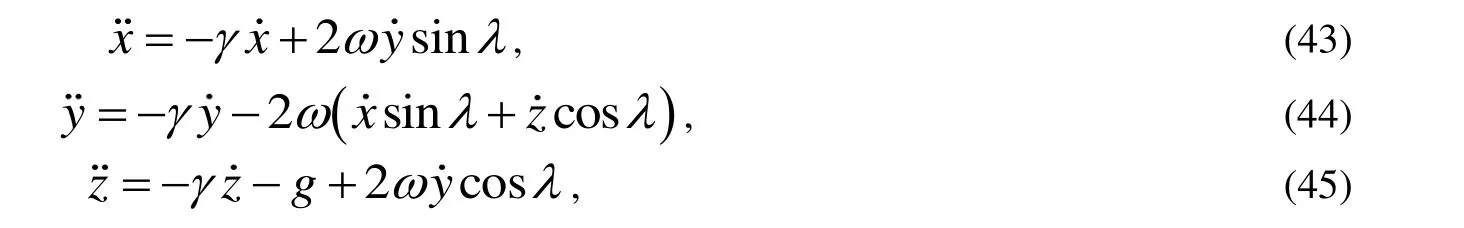
同時設拋體運動的初始條件為

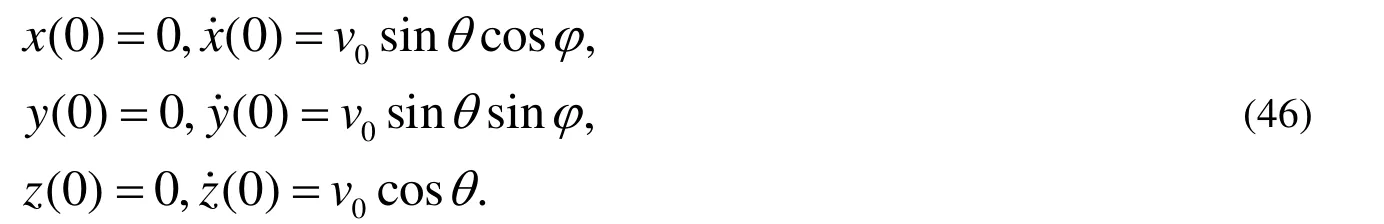
下面通過連續近似法得到該運動學方程的近似解。首先針對于式(43)～(45)首先積分，并代入初始條件式(46)得到

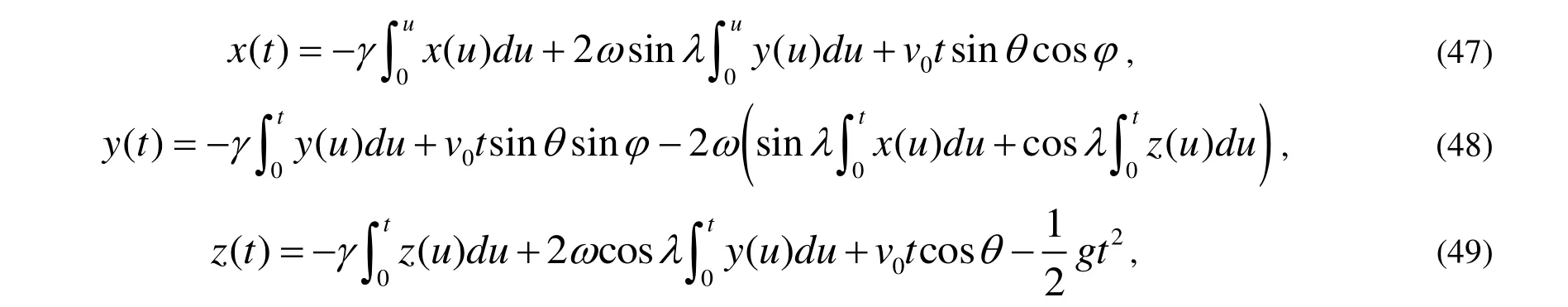
然后將式(47)～(49)中x(u)、y(u)、z(u)用初始條件式(46)中x(0)、y(0)、z(0)進行替換，就能得到一級近似解：

從以上三式可以看出一級近似解就是上文中拋體在只受重力下的運動學方程，并且將這個三式代入式(47)～(49)中x(u)、y(u)、z(u)后積分就能得到考慮空氣阻力與地球自轉的二級近似解：

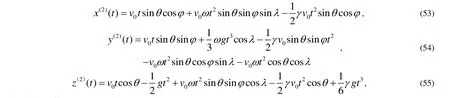
然后選取參數

然后畫出拋體運動圖像，如圖5 所示：

作為二級近似解的圖像，從圖5(a)就足以觀察到在x-z平面以不同的拋射角拋射的物體，在往x方向運動的同時因為受科里奧利力的影響產生沿-y方向上的微小位移，這同時也符合北半球運動的物體向右偏的現象。并且在圖5(b)中能夠觀查到相比于圖中其他拋射角，以π/4拋射的物體在x方向的射程最遠，而從圖(c)～(d) 卻發現以π/3拋射的物體在y軸方向射程最遠，這說明不同方向上最遠射程對應的拋射角不一樣。

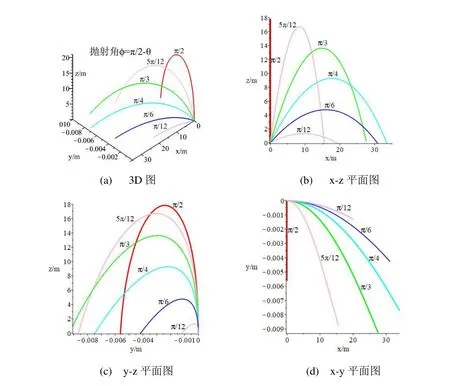
圖5 科里奧地力與阻力影響下的拋體運動

針對于二級近似解式(53)～(55)還可以用相同的方式帶入式(47)～(49)以求出更精確的三級近似解：

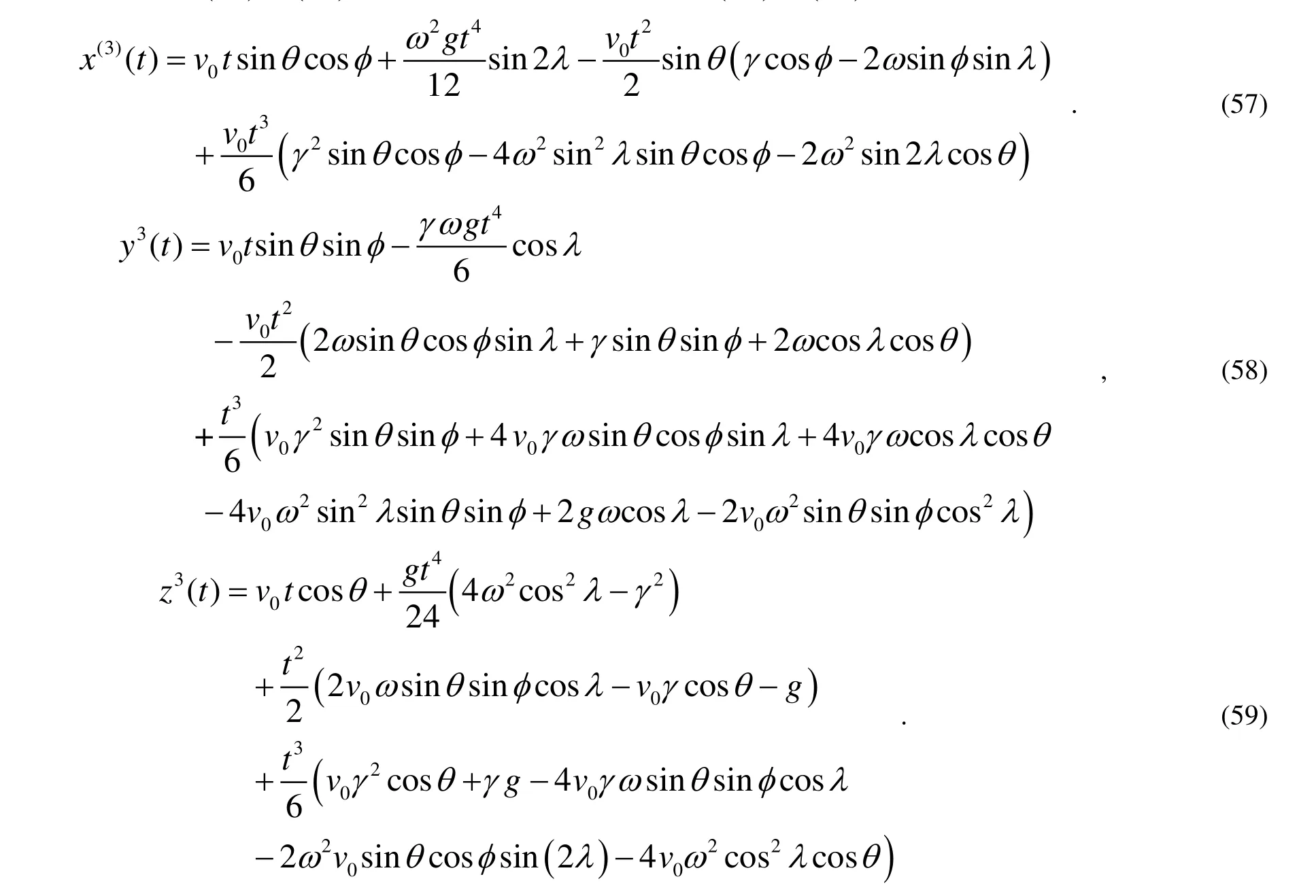
同時再設置參數：

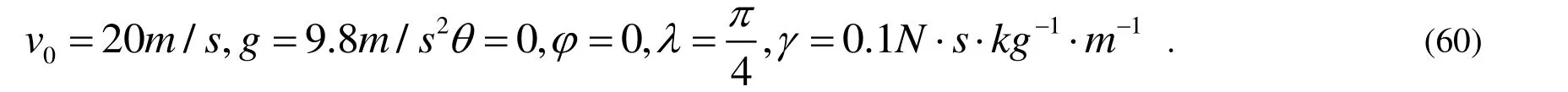
然后通過求式(43)～(45)求出其數值解與通過連續近似法得到結果進行比較，如圖6 所示

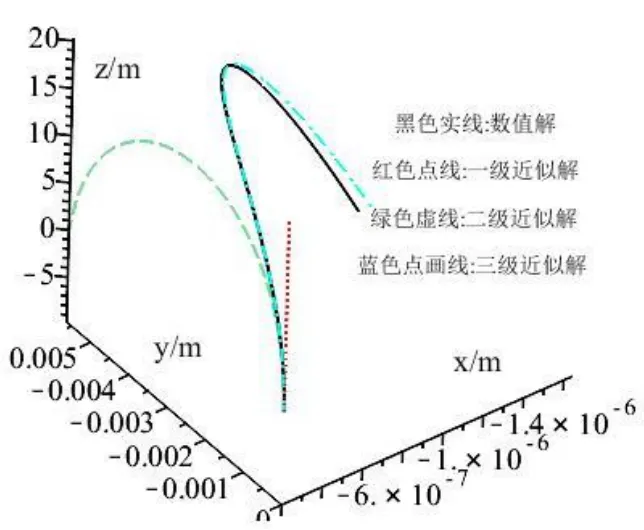
圖6 近似解與數值解的比較

從上圖可以發現代表一級近似的豎直上拋運動一開始就偏離了數值解，而二級近似解在運動往-y方向上偏移，也與數值解的差距越來越大.但作為三級近似解在整個拋體過程能較好的符合真實解。這說明隨著近似解不停地迭代，能更好的符合拋體真實的運動過程。

5 恒定風速作用下的拋體運動

拋體在真實的運動過程中除了上述討論的受重力、空氣阻力、科里奧利力之外，還可能會受到空氣的定向移動的影響，即風的作用。下文就綜合上述各種力下對探究水平方向恒定風速對拋體運動的影響。假設風速恒為V，則可以列出下列動力學方程：

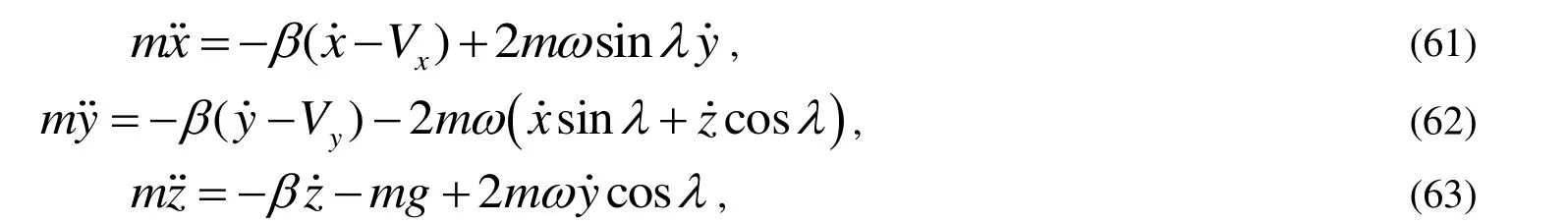
為了下文探討方便設fx=βVx/m,fy=βVy/m,γ=β/m，則上式可化簡為

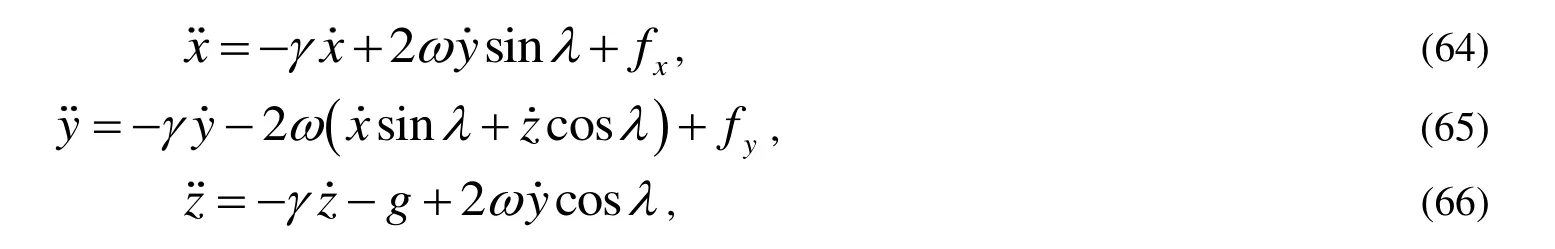
同時設初始條件為

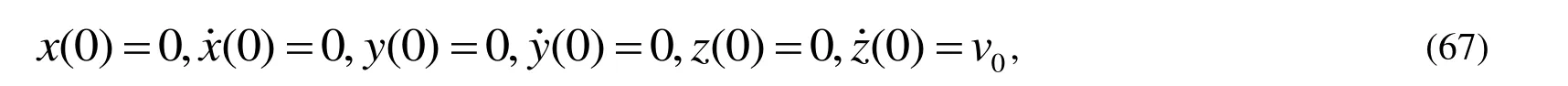
針對式(64)～(66)對時間t進行一次積分，并代入初始條件得到：

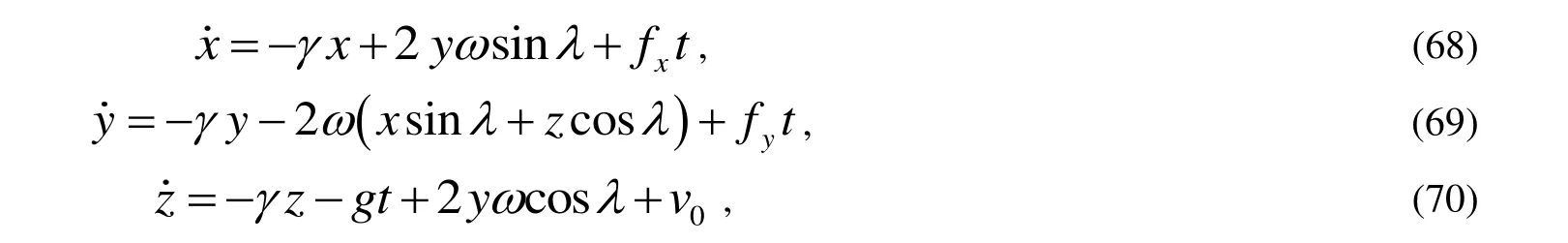
由以上三式可以得到:

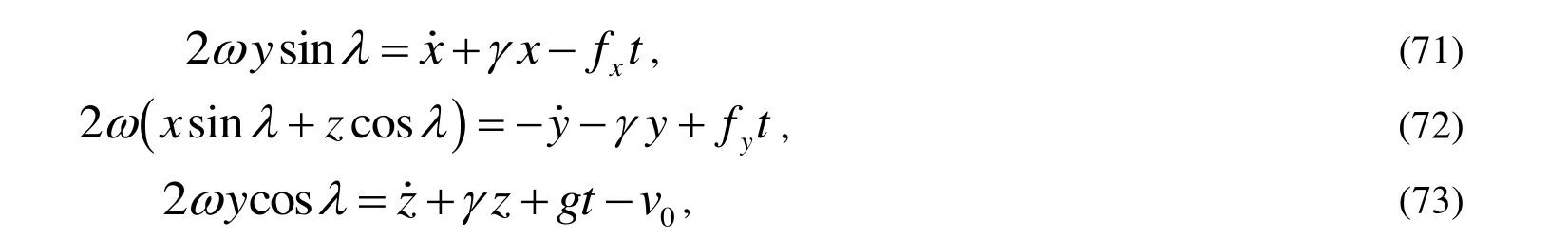
然后將式(68)～(73)代入式(64)～(66)，并忽略包含有ω2的項（地球自轉角速度過小）得到：

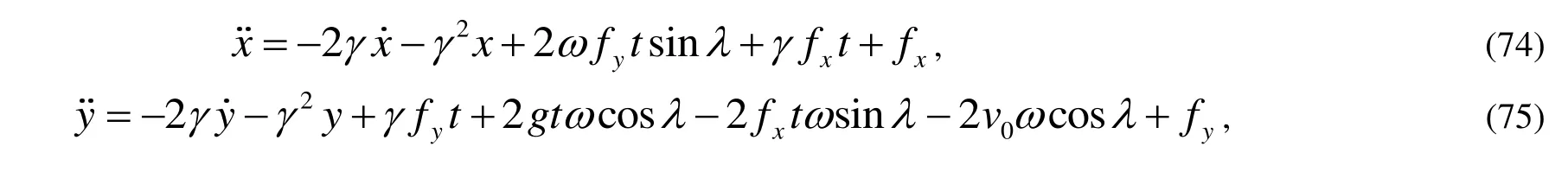
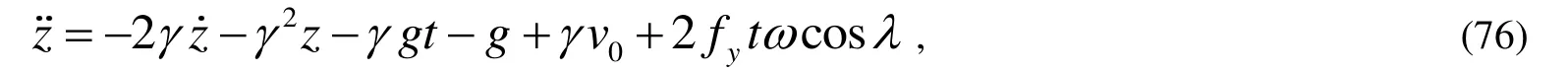
最后由初始條件式(67)解以上三式得到其運動的近似解為：

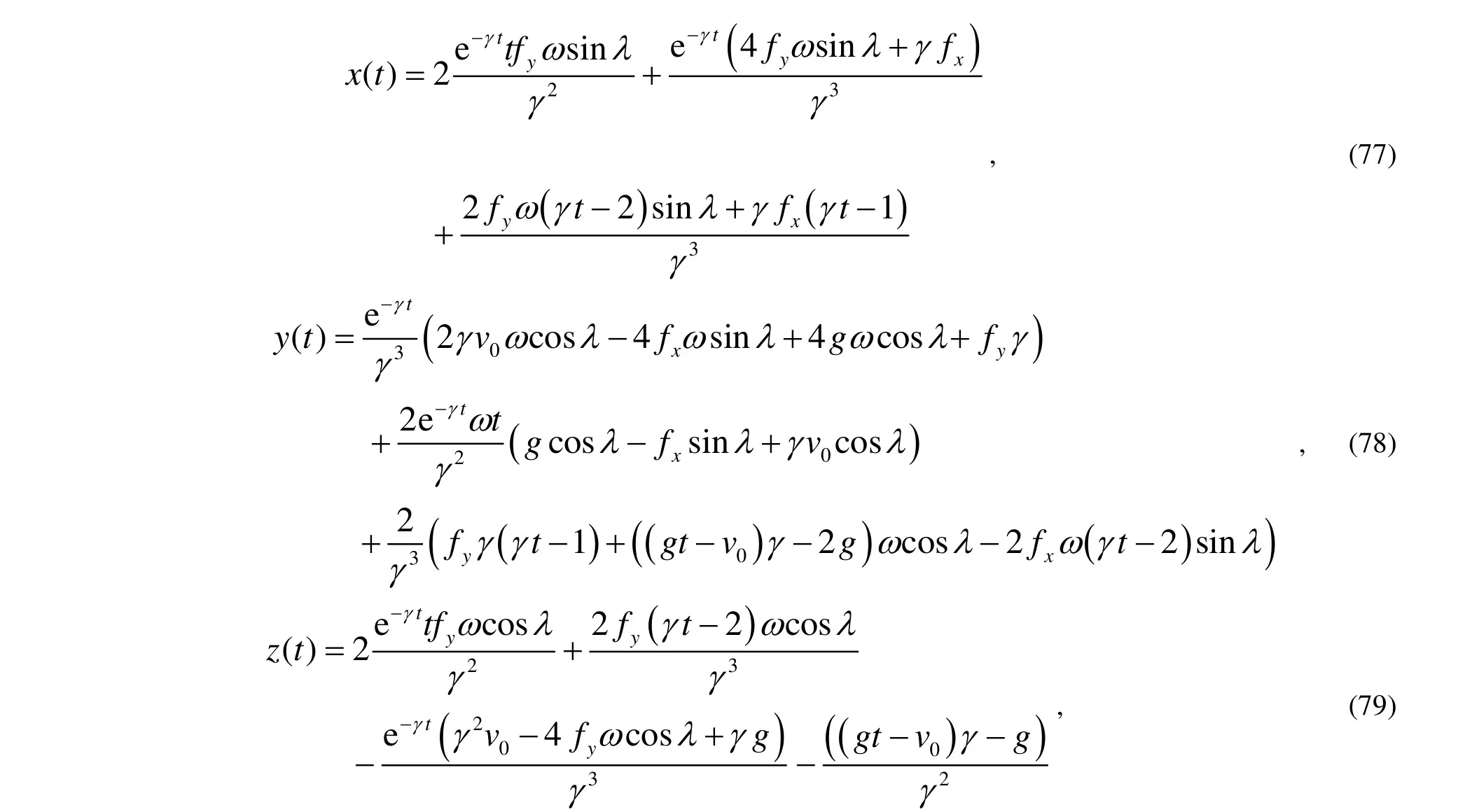
再設置參數：

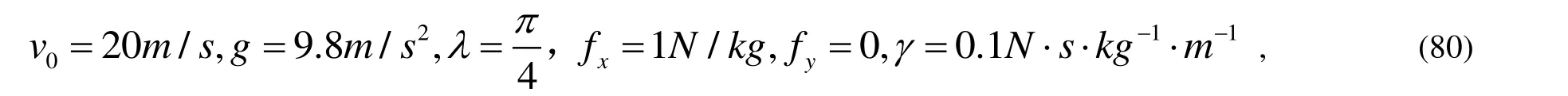
然后進行與數值解的比較，如圖7 所示：

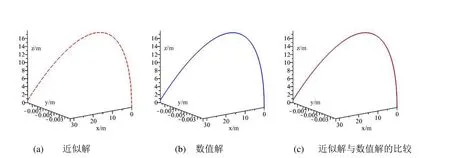
圖7 近似解與數值解

從上圖可以看出近似解與數值解的圖像近似完全重合，說明該近似解的表達式正確。并且從圖中還可以發現物體在豎直上拋的過程中受到沿x方向的風時會往x方向的大范圍移動的同時會受到科里奧利力的影響往y軸的負方向進行微小的偏移.此外改變風速大小得到如下圖像(圖8)

從圖8 觀察到隨著風力的增大，拋體不僅在風力的方向上位移增大，而且-y方向上的位移也逐漸變大.這說明沿x方向的風會影響拋體在y方向的運動。

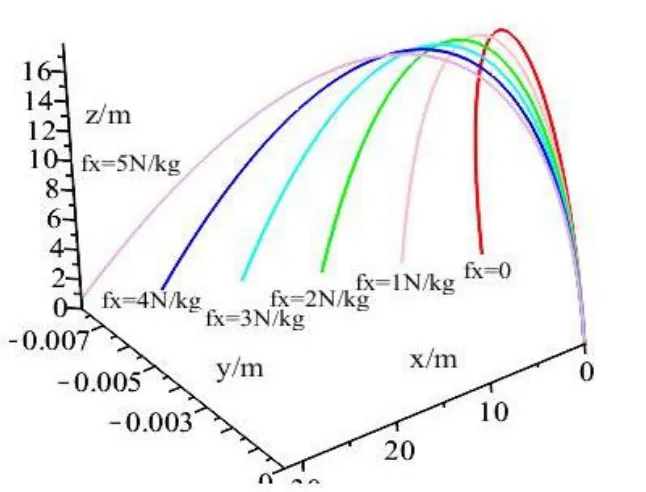
圖8 不同風速對拋體運動的影響

同時若在式(77)～(79)中令ω=0，然后對γ進行泰勒展開，得到

從以上三式可以看出當忽略地球自轉，并考慮無阻尼情況（γ=0 ），以上三式就過渡到只受重力情況下的豎直上拋運動

從而也側面驗證了式(77)～(79)的合理性。

6 結論

本文從牛頓力學的角度對拋體運動進行了詳細的研究，探究了拋體在受重力、空氣阻力、科里奧利力、風力等情況下的運動過程.求出拋體在受到這些力作用下的動力學方程的精確解或近似解，并研究與其相關的幾何性質。但值得指出的是本文雖然逐層遞進的方式來還原真實情況下的拋體運動，但是在考察空氣阻力的時候假設阻力與速度成簡單的線性關系的情況，而在真實情況中當拋體速度逐漸變大時，阻力會與速度大小的高次方成正比。因此本文在研究拋體運動性質時尚不夠全面，需要在以后的研究中更加深入和動態的考察空氣阻力與拋體速度的關系。