巧用生活情境原始問題 培養(yǎng)學(xué)生科學(xué)論證能力

卞志榮 焦建生

(江蘇省天一中學(xué)，江蘇 無錫 214101)

科學(xué)思維是物理核心素養(yǎng)的重要組成部分.其主要包括模型建構(gòu)、科學(xué)推理、科學(xué)論證、質(zhì)疑創(chuàng)新等要素.科學(xué)論證是一種基于科學(xué)知識、證據(jù)和推理以證實、辨明主張的實踐活動.科學(xué)論證能力是通過論證活動表現(xiàn)出來的一種復(fù)雜的綜合能力.要提高學(xué)生科學(xué)論證培養(yǎng)的實效性，教師必須依據(jù)科學(xué)理論設(shè)計高質(zhì)量的學(xué)生活動.當(dāng)前科學(xué)教育中開展論證活動中最重要的理論基礎(chǔ)是圖爾敏論證模式，由主張、資料、正當(dāng)理由、支援、限定和反駁等6個功能要素構(gòu)成的過程性模式，開啟了論證邏輯的實踐轉(zhuǎn)向.

由于生活類情境原始問題強(qiáng)調(diào)的是基于學(xué)生生活實際的真實情境，來源于學(xué)生生活實際，學(xué)生具備了一定的感性認(rèn)識，能引起學(xué)生學(xué)習(xí)興趣，激發(fā)學(xué)生的探究熱情，當(dāng)然有利于培養(yǎng)學(xué)生的科學(xué)論證能力.依據(jù)圖爾敏論證模式，在學(xué)生學(xué)過“超重與失重”之后，我們創(chuàng)設(shè)了以商場內(nèi)電子臺秤為背景的系列探究活動，有意識地對學(xué)生進(jìn)行科學(xué)論證能力培養(yǎng).

1 創(chuàng)設(shè)生活情境問題，培養(yǎng)學(xué)生科學(xué)論證習(xí)慣

教師在為學(xué)生創(chuàng)造科學(xué)論證機(jī)會之前，用PPT明確告訴學(xué)生，科學(xué)論證應(yīng)包括提出自己的觀點、提供與觀點相關(guān)的證據(jù)、聯(lián)系觀點和證據(jù)的推理過程以及反駁等流程.教師也可以通過具體情境問題的論證解決加以示范指導(dǎo)，包括論證方法的選用和證據(jù)的使用等，讓學(xué)生掌握科學(xué)論證的規(guī)律，在具體問題中加強(qiáng)科學(xué)論證過程的嚴(yán)密性培養(yǎng)，養(yǎng)成良好的論證習(xí)慣.

臺秤是生活中常見的用具，學(xué)生在大大小小商場司空見慣.筆者就以臺秤稱量重物為情景設(shè)計了學(xué)生探究活動，為學(xué)生提供科學(xué)論證機(jī)會，在論證中提高思維能力，同時強(qiáng)化超失重概念的學(xué)習(xí).

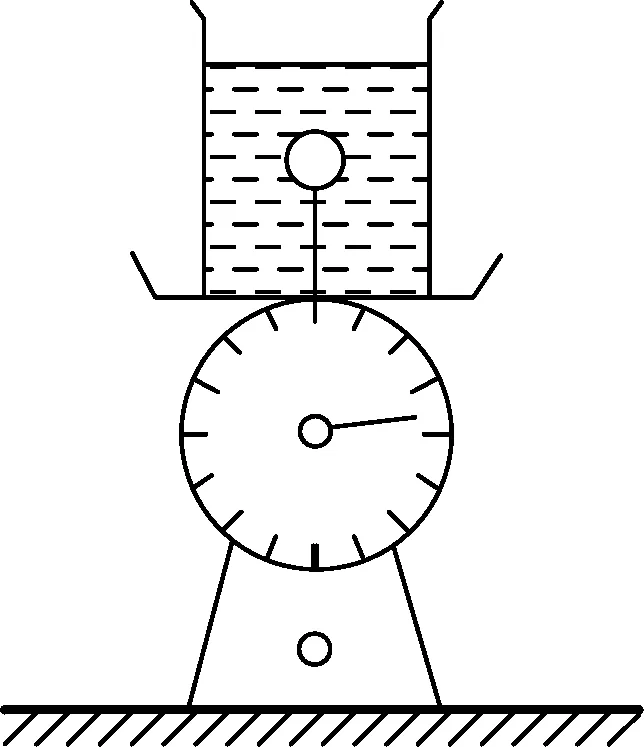
問題1.如圖1(甲)所示，臺秤上放有盛滿水的有機(jī)玻璃水杯，杯底用細(xì)線系一乒乓球，試論證細(xì)線被剪斷后，臺秤示數(shù)與未斷前有何變化？

猜想：絕大多數(shù)學(xué)生認(rèn)為“示數(shù)變大”.

論證：剪斷細(xì)線后，圖1(甲)中乒乓球加速上升，處于超重，所以臺秤示數(shù)變大；

實證：教師用課前準(zhǔn)備好的實驗器材進(jìn)行演示實驗，實驗裝置如圖1(乙)所示.電子臺秤規(guī)格：SF- 400，5000 g×1 g，有機(jī)玻璃筒上內(nèi)徑10 cm、下內(nèi)徑8 cm、高30 cm，乒乓球加懸線質(zhì)量2 g，懸線下端系一小螺帽，隔著瓶底用強(qiáng)磁鐵吸住螺帽.為了方便手移走磁鐵釋放乒乓球，用三腳架撐起玻璃筒一起放在臺秤上.移走磁鐵釋放乒乓球使其上浮，觀察球上浮過程臺秤示數(shù)變化.本次實驗上浮前臺秤示數(shù)1580 g，上浮時示數(shù)為1571 g，臺秤示數(shù)變小.與學(xué)生的猜想不一致，產(chǎn)生認(rèn)知沖突.

(甲)

(乙)
圖1

再論證：在教師的引導(dǎo)下，學(xué)生經(jīng)過一番討論，終于找到了正確科學(xué)的論證方法：乒乓球加速上升的同時有同樣體積的水球以同樣的加速度下降，乒乓球處于超重而水球處于失重，因同體積水球質(zhì)量大于乒乓球質(zhì)量，所以失重大于超重，綜合起來系統(tǒng)處于失重，所以臺秤示數(shù)變小，而不是變大.

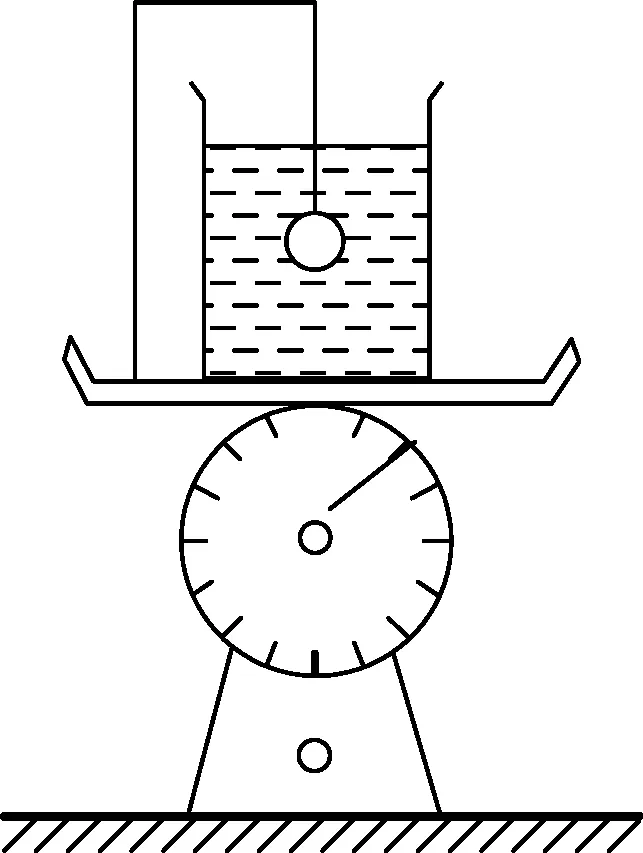
問題2.如圖2(甲)所示，臺秤上放有盛滿水的有機(jī)玻璃水杯，小鐵球(直徑2.5 cm)懸掛在固定于臺秤上的支架上且浸沒在水中，不計水的阻力，試論證細(xì)線被剪斷后，臺秤示數(shù)與未斷前有何變化？

觀點：臺秤示數(shù)變小.

論證：支架、鐵球及線、水和杯構(gòu)成一個整體，燒斷細(xì)線前臺秤測得是它們的總重量，燒斷細(xì)線后鐵球所受重力大于浮力，向下加速下降，處于失重狀態(tài)，所以臺秤示數(shù)變小.

實證：實驗裝置如圖2(乙)所示，將小球懸掛在鐵架臺上，將直徑2.5 cm的鐵球用細(xì)線懸掛在鐵架臺上，為了防止鐵球下落砸壞水杯，在杯底墊上海綿，整個裝置一起放在臺秤上，細(xì)線燒斷前臺秤示數(shù)為3441 g，燒斷后臺秤示數(shù)為3423 g，確實減小，證明了學(xué)生論證的正確性.

(甲)

(乙)
圖2

總結(jié)：要判斷臺秤示數(shù)變化就是判斷水杯對臺秤的壓力變化.大部分學(xué)生能很快建立起超失重模型，定性分析論證，比較快捷地得出結(jié)論.說明這部分學(xué)生對這個問題具備了一定的科學(xué)論證能力.少數(shù)學(xué)生采用最常規(guī)方法：通過受力分析再用牛頓第二定律列方程進(jìn)行定量論證，往往卡在球與水、水與杯的作用力問題上而裹足不前.這說明論證方法的優(yōu)劣會影響論證過程的快捷、準(zhǔn)確程度.還有部分學(xué)生對圖中情境缺乏全面考慮致使論證結(jié)論出現(xiàn)差錯.所以，論證過程必須嚴(yán)謹(jǐn)，論證材料必須全面、科學(xué).從這里我們還可以體會到論證方法的多樣性，如理論論證中的定性、定量論證；事實論證中的實驗論證等.以后我們還會遇到比較論證、因果論證等方法.為了檢驗學(xué)生論證習(xí)慣和能力以及論證方法的靈活性，筆者又提供了情境相似但有變化的問題，讓學(xué)生再論證，優(yōu)化論證方法.

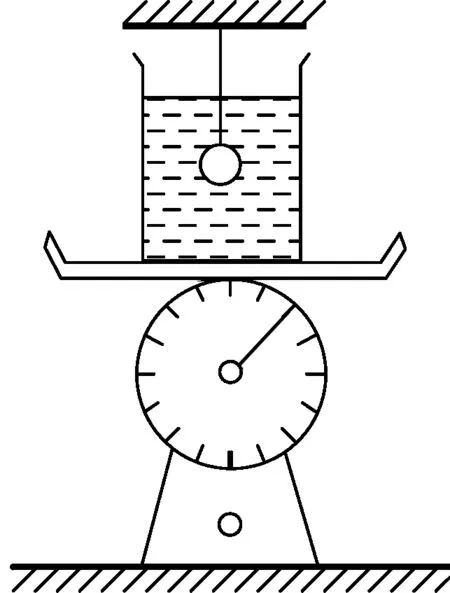
問題3.如圖3(甲)所示，將小鐵球懸掛在鐵架臺上且浸沒在水中，燒斷細(xì)線后，在小球向下運動過程中臺秤的示數(shù)與剪斷前相比變大還是變小？

猜想：大部分學(xué)生觀察不夠細(xì)致，認(rèn)為與問題2一樣，臺秤示數(shù)變小.

引導(dǎo)：引導(dǎo)學(xué)生觀察情境問題3與問題2中懸掛鐵球的方式有何不同？(問題3中小鐵球是懸掛在臺秤以外，而問題2中小鐵球是懸掛在臺秤上)，情境不同，當(dāng)然不能盲目套用2中的論證方法，怎么辦呢？讓學(xué)生分組討論后得出，必須巧選研究對象，用定量論證的方法才能解決.

(甲)

(乙)

(丙)

圖3

論證：因為小球懸掛在臺秤以外，懸線燒斷前，要研究臺秤受到的壓力，必須以水和杯為研究對象.設(shè)水和水杯總重為G，鐵球質(zhì)量m鐵，受到水的浮力為F浮，受力分析可知，臺秤示數(shù)N=G+F浮.燒斷懸線后，設(shè)鐵球向下加速度大小為a，同體積的水球向上加速度大小也為a，要研究臺秤受到的壓力，隔離水和水杯，應(yīng)用牛頓第二定律得到N′-G-F浮=m水球a.所以N′=G+F浮+m水球a，顯然大于N，所以臺秤示數(shù)比剪斷前要大.

實證：實驗裝置如圖3(乙)所示，細(xì)線燒斷前臺秤示數(shù)2127 g，燒斷后示數(shù)為2183 g.

2 精選生活情境問題，讓學(xué)生體驗科學(xué)論證過程

教師可以在課堂中提出一些生活中的開放性問題來引發(fā)學(xué)生討論、思考，充分讓學(xué)生陳述自己的觀點和想法，并根據(jù)學(xué)生的回答進(jìn)行追問，如“你為什么這么想”、“你是怎么得到這個結(jié)論的”. 當(dāng)學(xué)生遇到困難時，教師通過搭建“腳手架”幫助學(xué)生探究原認(rèn)知中的不足之處，使學(xué)生重新構(gòu)建正確的推理過程.這樣在生生、師生互動中，讓學(xué)生對彼此的觀點和推理過程進(jìn)行相互評判，指出各自推理過程中可能存在的疑惑或自相矛盾的地方，激發(fā)學(xué)生再次審視問題中的條件和信息，反思自己的觀點，爭取用更多的證據(jù)來改正或支持自己的觀點.從而認(rèn)識原始論證過程和科學(xué)論證過程之間的差異，促進(jìn)學(xué)生逐步走上科學(xué)論證的新臺階.

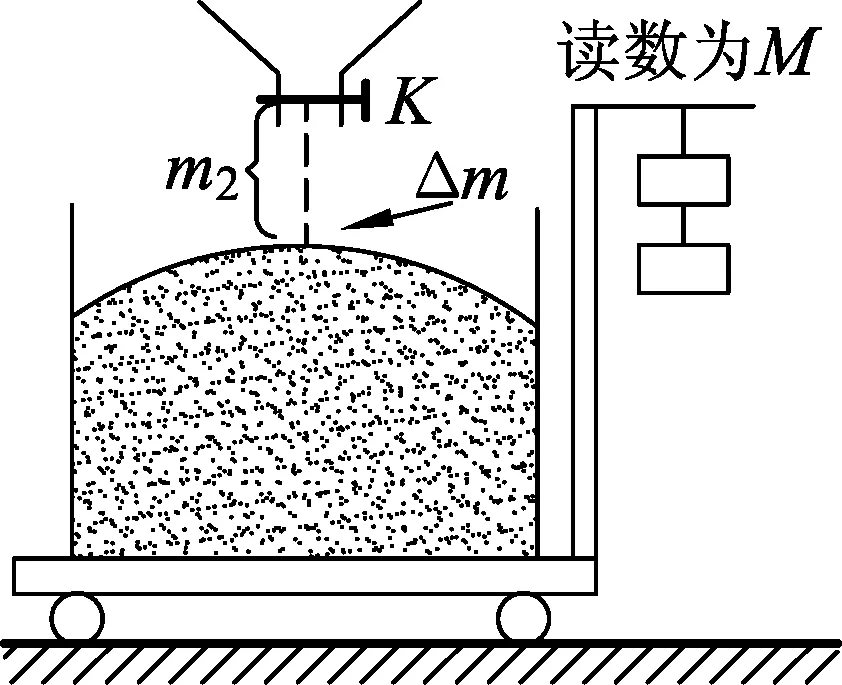
圖4

問題4.自動稱米機(jī)已被許多大糧店廣泛使用，原理圖如圖4所示.買者認(rèn)為：因為米流落到容器中時有向下的沖力而不劃算；賣者則認(rèn)為：當(dāng)預(yù)定米的質(zhì)量數(shù)滿足時，自動裝置即刻切斷米流時，此刻尚有一些米仍在空中，這些米是多給買者的，因而雙方爭執(zhí)起來，究競哪方說得對呢？

觀點：問題拋出之初，學(xué)生中存在3種觀點：

(1) 同意買者觀點，認(rèn)為買者說得有道理.

(2) 同意賣者觀點，認(rèn)為賣者說得有道理.

(3) 認(rèn)為買者觀點和賣者觀點都不對，應(yīng)該是準(zhǔn)確的，否則還有誰用這種秤呢？

引導(dǎo)：這是一道原始物理問題，讀完題目買賣雙方說的似乎都有道理，但又無法說清為什么，即論證理由不充分或論證方法找不到.但我們至少應(yīng)該堅信的是：這是一道力學(xué)問題，解決力學(xué)問題首先得確定研究對象，進(jìn)行受力分析.遇到這種較為復(fù)雜的原始問題，我們應(yīng)該冷靜下來進(jìn)行理性思考，猜想此問題可能會用到什么物理知識和規(guī)律，聯(lián)想、類比曾經(jīng)遇到過的類似問題，或許能很快找到論證的方法.

我們是否可以這樣思考：

(1) 臺秤的讀數(shù)是物體對秤盤的壓力；

(2) 米是固體，但米流和流體相似；

(3) 處理流體問題常常要建立柱狀模型，如水力采煤求水對煤層的沖力；風(fēng)力發(fā)電求風(fēng)對葉片的作用力等；

(4) 求變化的物理量的常用方法是微元法.

論證：設(shè)米流的流量為d，它是恒定的，自動裝置能即刻在出口處切斷米流，米流在出口處速度很小可視為0.若切斷米流后，盛米容器中靜止的那部分米的質(zhì)量為m1，空中還在下落的米質(zhì)量為m2，取已靜止米堆m1上方在空中的一小部分米柱Δm為研究對象，經(jīng)過Δt(Δt→0)時間落至米堆內(nèi)，則Δm=d·Δt.設(shè)其落到米堆上之前的速度為v，其受到重力Δmg和已靜止米對它的作用力F的作用，經(jīng)Δt由速度v變?yōu)殪o止.由動量定理得

(F-Δmg)Δt=Δmv，即F=dv+dgΔt.

設(shè)米從出口處落到米表面所用的時間為t，由于m2=d·t，v=gt(阻力不計)，所以，d·v=m2·g，即F=m2g+Δmg.根據(jù)牛頓第三定律知F=F′，所以，稱米機(jī)讀數(shù)應(yīng)為

結(jié)論：由以上定量論證可見，稱米機(jī)讀數(shù)包含了靜止在袋中的部分m1，也包含了尚在空中的下落的米流m2，還包含了剛落至米堆上的一小部分Δm，即自動稱米機(jī)是準(zhǔn)確的，不存在誰劃算不劃算的問題.

總結(jié)：運用物理知識解決實際生活問題，必須把實際問題轉(zhuǎn)化為物理模型和物理過程，依據(jù)所學(xué)知識和思維方法進(jìn)行分析推理，建立不同物理量間的聯(lián)系是科學(xué)論證中的關(guān)鍵所在.論證能力的提高需要在實踐中不斷體驗、感悟.

3 活用生活情境化試題，提升學(xué)生科學(xué)論證能力

情境化試題是指以自然界及社會生活、生產(chǎn)中客觀存在的物理現(xiàn)象或過程為背景，考查學(xué)習(xí)者對物理概念、規(guī)律的理解與應(yīng)用能力的試題.論證解決這類試題的基本流程如圖5所示.

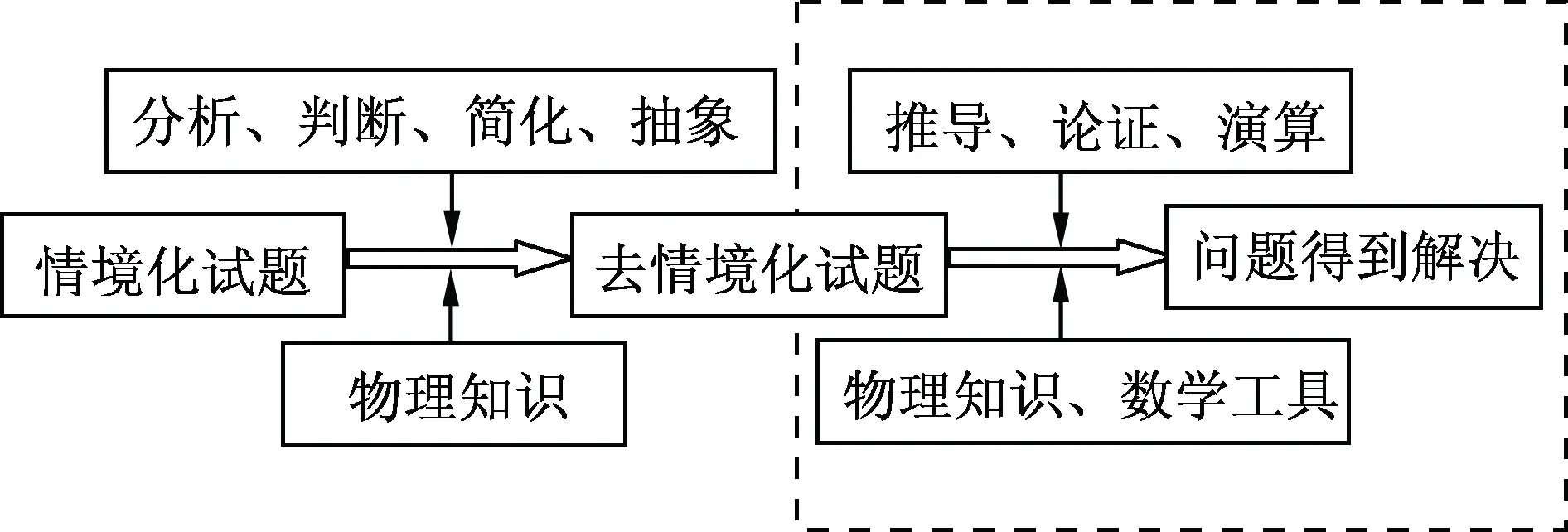
圖5

新課程《標(biāo)準(zhǔn)》中明確指出，在教學(xué)設(shè)計和教學(xué)實施過程中要重視情境的創(chuàng)設(shè).試題的情境要具有一定的問題性、真實性、探究性或開放性.設(shè)問的角度及方式要科學(xué)、可信、新穎、靈活.要求通過學(xué)生在應(yīng)對復(fù)雜現(xiàn)實情境，參與相應(yīng)探究學(xué)習(xí)活動中的外在表現(xiàn)來考查物理學(xué)科核心素養(yǎng)，在解決具體問題中體現(xiàn)和提升物理科學(xué)論證能力.

近年來，情境化試題在高考等選拔考試中也得到重視和應(yīng)用.如國外流行的基于問題學(xué)習(xí)模式(PBL)等都非常強(qiáng)調(diào)把學(xué)習(xí)內(nèi)容“嵌套”在實際問題中或真實的社會情境中；國際大型測評項目PISA，在其考試中主要使用此類試題.我們在運動學(xué)學(xué)習(xí)之后呈現(xiàn)給學(xué)生的情境問題是來自伊朗物理競賽預(yù)賽試題.

問題5.打開水龍頭，水就流下來，為什么連續(xù)的水流柱的直徑在流下過程中減小？假設(shè)水龍頭開口直徑為1 cm，安裝在75 cm高處.如果水在出口處的速度為1 m/s，求水流柱落到地面處的直徑有多大？(不計空氣阻力，g=10 m/s2)

觀察：試題呈現(xiàn)出來后，學(xué)生也覺得題中所敘情境是生活中很常見，但好多學(xué)生一籌莫展，遲遲不能下手.究其原因反映出現(xiàn)在的好多學(xué)生在生活中不善于觀察和思考，就連越流越細(xì)也沒有印象，遇到來自身邊的實際問題也不能順利地將所學(xué)知識遷移到情境之中而得到解決.

引導(dǎo)：就試題本身來說，第一問屬于原始物理問題，第二問進(jìn)行了賦值變成了物理習(xí)題.要找到解決問題的辦法，必須結(jié)合題目敘述的情景進(jìn)行以下邏輯推理，方能找到論證方法.

(1) 研究對象是水.

(2) 水流做的是什么運動？

(3) 下面的水與上面的水的運動有什么不同？

(4) 上、下水流流速相同嗎？

(5) 什么是它們聯(lián)系的紐帶？

通過以上幾個“為什么”，就不難發(fā)現(xiàn)：水不管在什么高度，通過某一水平截面相同的時間內(nèi)流過的水的體積(或質(zhì)量) 相同，同時由于水在不同高度速度不等，需要用“微元法”化變?yōu)椴蛔儯ⅵ(Δt→0)時間內(nèi)的柱狀模型.

論證： (1) 在時間t內(nèi)，流過任一水柱截面的水的體積是一定的，由于水柱頂點的水速小于下面部分的水速，故水柱的直徑上面比下面大.

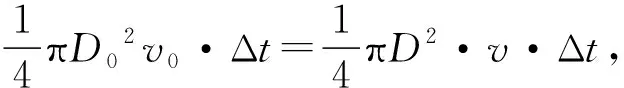
教師總結(jié)：該題屬于聯(lián)系實際的創(chuàng)新題，既不超出考綱要求，又能很好地考查學(xué)生分析解決實際問題的能力.同時我們又從以上論證中感悟到：解題的過程就是運用歸納推理將文字信息轉(zhuǎn)化為問題情境，然后運用演繹推理將情境轉(zhuǎn)化為物理條件，再選擇物理規(guī)律和方法進(jìn)行科學(xué)論證的過程，在問題解決中實現(xiàn)論證能力的提升.

通過以上系列情境問題的論證教學(xué)之后，學(xué)生不僅掌握了科學(xué)論證過程和方法，論證能力也得到了一定程度的提升.學(xué)生在論證過程中感悟到了物理問題來自于生活，學(xué)習(xí)物理知識又可以服務(wù)于生活的哲學(xué)道理，真正理解到“物理即生活”的精神內(nèi)涵.在平時教學(xué)中，教師要加強(qiáng)STSE教學(xué)，引導(dǎo)學(xué)生善于觀察生活，了解社會，關(guān)注科技，善于發(fā)問，敢于質(zhì)疑，將所學(xué)知識和能力遷移到實際問題中，做到學(xué)以致用.教師要為學(xué)生多提供生活類情境問題，進(jìn)行科學(xué)論證訓(xùn)練，在訓(xùn)練中發(fā)展學(xué)生的思維能力，提升科學(xué)素養(yǎng).