數據分析,從真實情境出發
王小亮
近幾年全國卷統計知識部分,主要基于現實世界中生產、生活等真實情景,結合圖表(頻率分布直方圖、折線圖、餅圖或頻數(率)分布表,2×2 列聯表等),考查同學們的數據分析能力.數據分析包括:快速收集、整理數據,分析數據,最終利用數據給出正確合理的判斷.以下就通過高考題一起來看看吧。
一、平均值、方差
例1 (2019 年全國Ⅲ卷)為了解甲、乙兩種離子在小鼠體內的殘留程度,進行如下試驗:將200 只小鼠隨機分成A,B 兩組,每組100 只,其中A 組小鼠給服甲離子溶液,B組小鼠給服乙離子溶液,每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比.根據試驗數據分別得到如下直方圖:
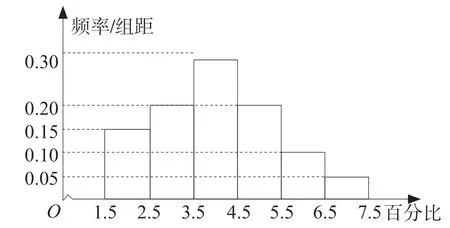
甲離子殘留百分比直方圖
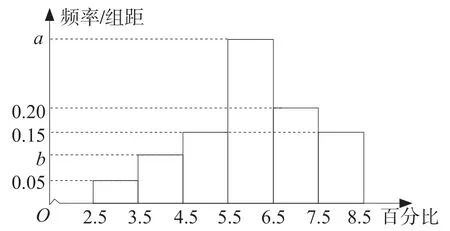
乙離子殘留百分比直方圖
記C 為事件:“乙離子殘留在體內的百分比不低于5.5”,根據直方圖得到P C( )的估計值為0.70.
(1)求乙離子殘留百分比直方圖中a,b 的值;
(2)分別估計甲、乙離子殘留百分比的平均值(同一組中的數據用該組區間的中點值為代表).
分析

(1) 文字 圖形 知識點條件 P C( )的估計值為0.70 [6.5,7.5),[7.5,8.5]對應小矩形的高頻組率 距 分別為0.20,0.15(乙圖)所有小矩形面積(即頻率)之和為1轉化 [5.5,8.5]的頻率和0.70 兩組頻率和(0.20 0.15) 1+ × (組距)=0.35結論a=0.70 0.35( )1組?距 =0.35,b= ? ? ? =1 0.70 0.15 0.05 0.10

(2) 文字 圖形 知識點條件 提供真實情境 提供組中值和對應頻率相關信息 平均值公式轉化 數據的實際意義 根據圖甲、乙可求組中值和對應頻率(略)結論 甲,乙平均值分別為4.05,6.00(解答過程略)n 1 x x p=∑i=i i
【歸納提升】
二、獨立性檢驗
例2 (2017 年全國Ⅱ卷)海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100 個網箱,測量各箱水產品的產量(單位:kg),其頻率分布直方圖如下:
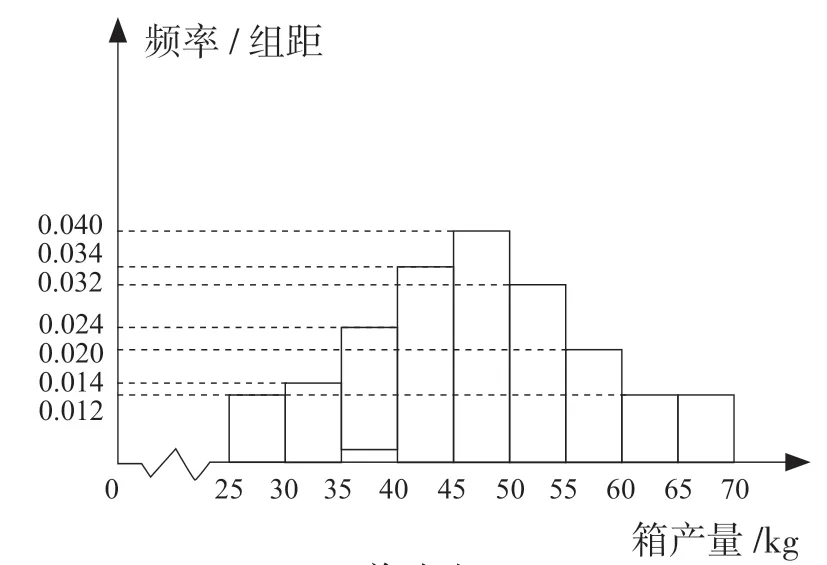
舊養殖法
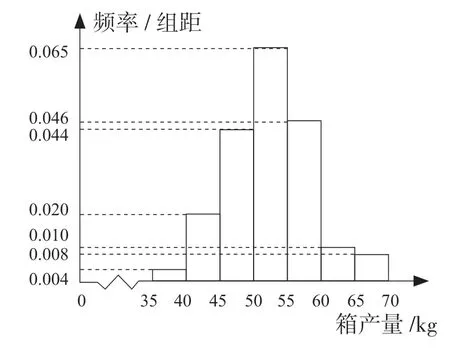
新養殖法
(1)記A 表示事件“舊養殖法的箱產量低于50 kg”,估計A 的概率;
(2)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關:

箱產量<50 kg 箱產量≥50 kg舊養殖法新養殖法
(3)根據箱產量的頻率分布直方圖,對這兩種養殖方法的優劣進行比較.
二是利用現代化手段,建立信息化服務平臺。Z公司累計投入300余萬元,建立軍民融合資源信息服務系統。首先,構建由技術資源、專家資源、科技項目、技術需求等信息共同組成的技術創新信息庫。信息庫內共包含各類相關信息近七萬條。其次,建立信息集成發布平臺。將與智能制造、新材料相關的產業政策、研發成果、科技動態等信息在平臺上進行匯集、整合、發布,使平臺上的信息既有深度又有廣度,充分發揮了該平臺的資源共享功能。
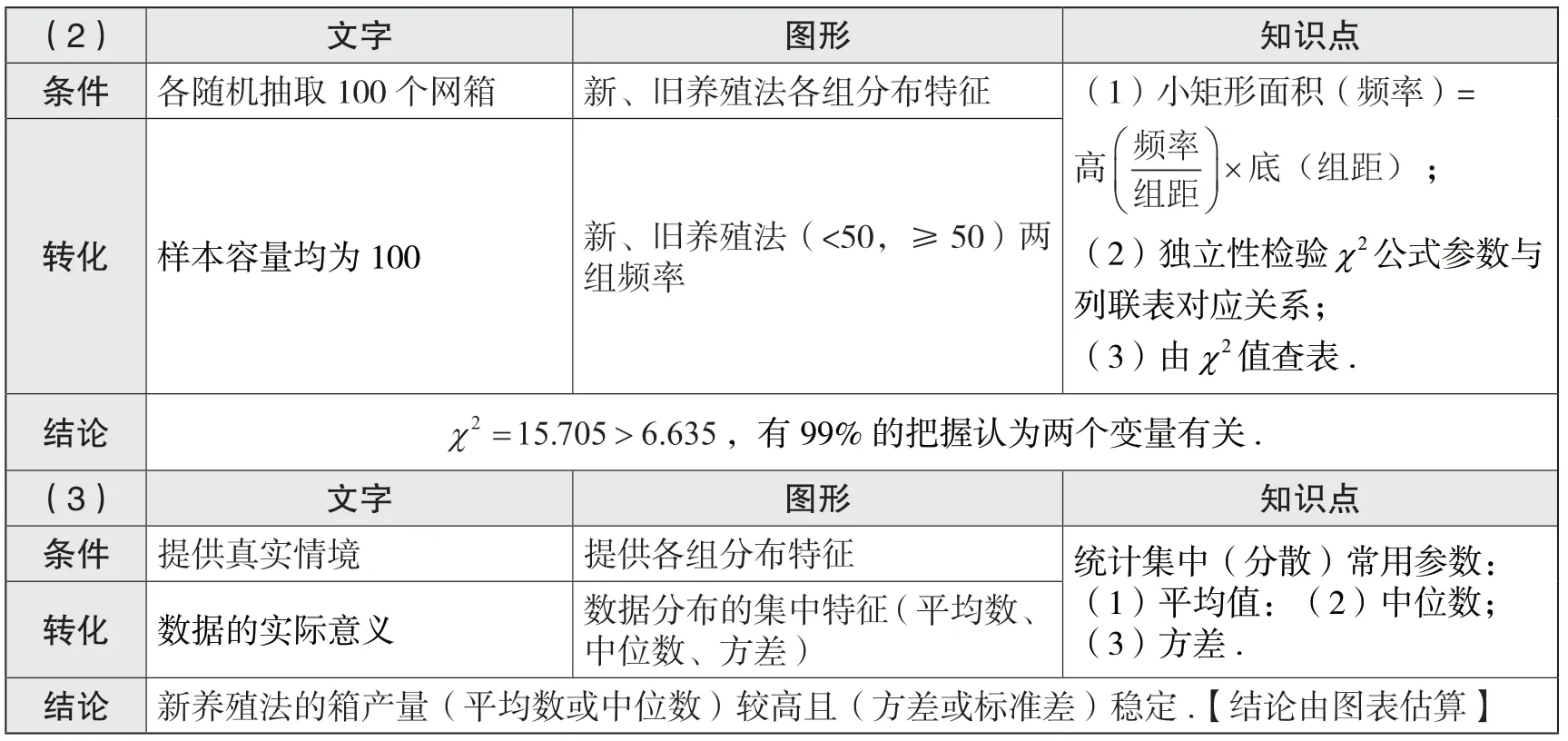
(2) 文字 圖形 知識點條件 各隨機抽取100 個網箱 新、舊養殖法各組分布特征 (1)小矩形面積(頻率)=高 頻率組距 ×底(組距);轉化 樣本容量均為100 新、舊養殖法(<50,≥50)兩組頻率(2)獨立性檢驗χ2 公式參數與列聯表對應關系;(3)由χ2 值查表.結論 χ2 = >15.705 6.635,有99%的把握認為兩個變量有關. (3) 文字 圖形 知識點條件 提供真實情境 提供各組分布特征 統計集中(分散)常用參數:(1)平均值:(2)中位數;(3)方差.轉化 數據的實際意義 數據分布的集中特征(平均數、中位數、方差)結論 新養殖法的箱產量(平均數或中位數)較高且(方差或標準差)穩定.【結論由圖表估算】
【歸納提升】
獨立性檢驗與計算平均值、方差比較:
(1)相同點:
① 篩選文字語言有效數據,理解相關數據實際含義;
② 主要抓住圖表提供數據信息;
(2)不同點:獨立性檢驗計算量略顯復雜,特別是代數據找好與列聯表對應關系.
三、成對數據的相關性
例3 (2016 年全國Ⅲ卷)下圖是我國2008 年至2014 年生活垃圾無害化處理量(單位:億噸)的折線圖
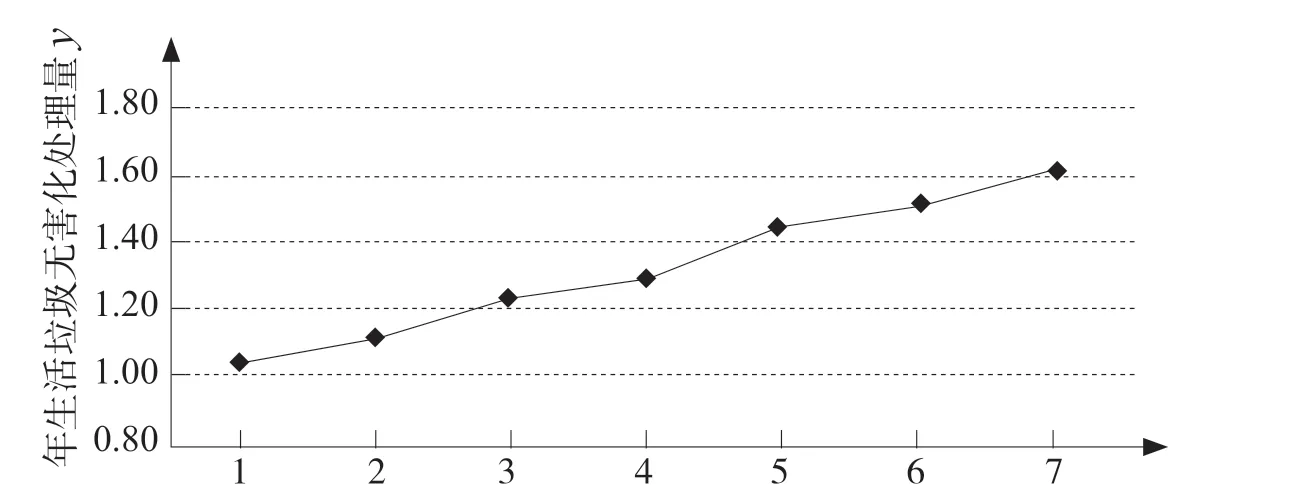
年份代碼t
(1)由折線圖看出,可用線性回歸模型擬合y 與t 的關系,請用相關系數加以說明;
(2)建立y 關于t 的回歸方程(系數精確到0.01),預測2016 年我國生活垃圾無害化處理量.
分析
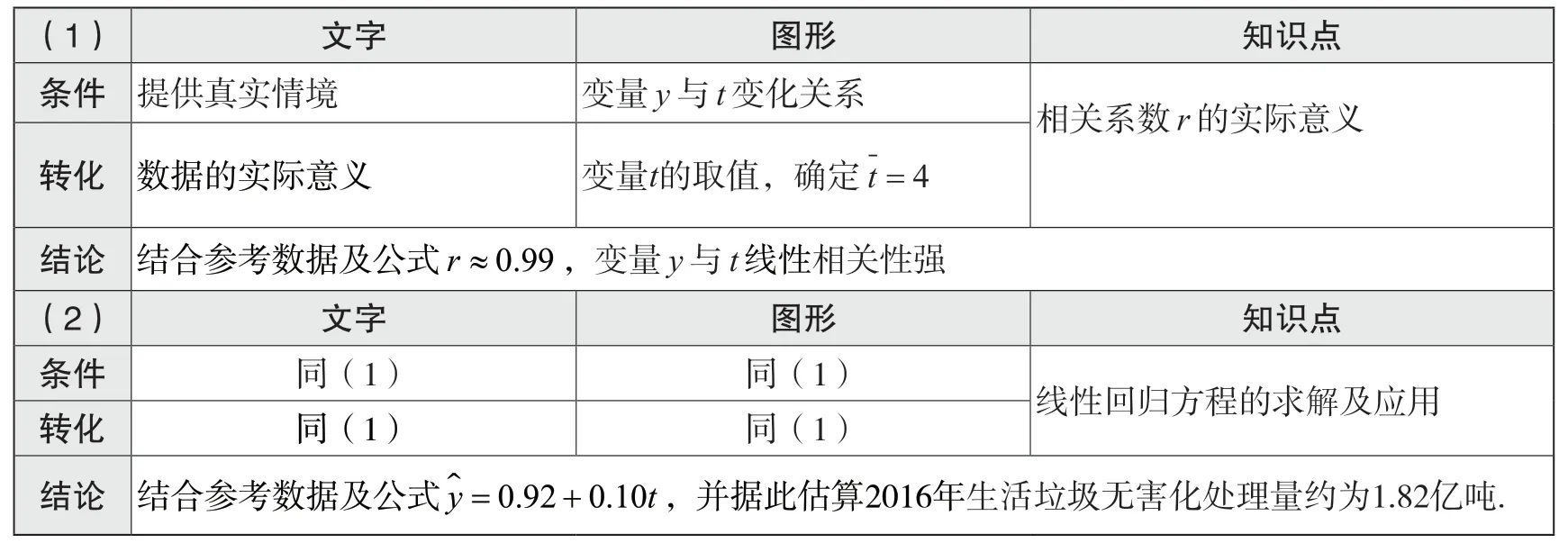
(1) 文字 圖形 知識點條件 提供真實情境 變量y 與t 變化關系 相關系數r 的實際意義轉化 數據的實際意義 變量t的取值,確定t=4結論 結合參考數據及公式r ≈0.99,變量y 與t 線性相關性強(2) 文字 圖形 知識點條件 同(1) 同(1) 線性回歸方程的求解及應用轉化 同(1) 同(1)結論 結合參考數據及公式?y t= +0.92 0.10 ,并據此估算2016年生活垃圾無害化處理量約為1.82億噸.
【歸納提升】
成對數據相關性與獨立性檢驗相比而言,雖都是套公式,但前者計算量更大,注意用好所給相關數據、公式外,建議把公式分成若干部分,分步計算.
高考中統計的考查更多的是和概率結合問題,而且難點出現在概率問題中.因此對概率問題的深度研究是解決高考中概率與統計問題的保障!
敲黑板
應對統計相關試題,同學們需要做到:
(1)抓住圖表中主要數據;
(2)快速認清真實情景,篩選有效數據(特別是文字量大的問題);
(3)準確快速運算;
(4)解答過程的規范書寫.

