基于微分幾何實現三維Dubins 路徑

黃金芬

（西華大學計算機與軟件工程學院，成都610039）

0 引言

無人機飛行路徑規劃是無人機自主控制中重點設計的一環，無人機的飛行路徑需要考慮無人機的約束條件。Dubins 路徑不僅符合無人機的飛行特性，而且是兩個位姿點間的最短路徑，因此，結合Dubins 路徑來規劃無人機飛行路徑是有利的。當前，Dubins 路徑主要用于無人機等高飛行路徑規劃，即類似于二維平面上的飛行，很少用于無人機變高飛行路徑規劃，即無人機在三維空間中的飛行。導致這種現象的一個重要原因就是三維Dubins 路徑很難求解。當前常見的求解三維Dubins 路徑的方法是先求出兩個位姿點在二維平面上的Dubins 路徑，然后結合螺旋線將二維Dubins 路徑轉為三維Dubins 路徑，但這種方法存在使用范圍受限的缺陷[1]。

Dubins 路徑可被簡單地定義為，在最大曲率限制下，兩位姿點間的最短可行路徑，可以是CSC 路徑或CCC 路徑，或是它們的子集（CS、CC、SC），其中C 表示圓弧段，S 表示與C 相切的直線段[2]。本文主要討論CSC 型Dubins 路徑。

Shanmugavel 等人做了大量關于Dubins 路徑的研究[3-5]。文獻[3]介紹了基于微分幾何求解二維Dubins路徑的方法；文獻[4]介紹了基于微分幾何求解帶有Clothoid 曲線的Dubins 路徑的方法；文獻[5]提供了基于微分幾何求解三維Dubins 路徑的思路，但沒有給出具體的求解方法。本文結合文獻[5]提出的思路對基于微分幾何求解三維Dubins 路徑的方法進行詳細解析。

1 基本知識

1.1 參數定義

計算Dubins 路徑前需要指定一些參數信息，下面對涉及的參數在二維和三維中有區別的分二維和三維來描述，其余的統一描述。

二維路徑中的參數定義如下：

（1）起始位姿點：ps(xs,ys,θs)。

（2）起始位姿點方向向量：ds，ds=[cosθssinθs]。

（3）終止位姿點：pf(xf,yf,θf)。

（4）終止位姿點方向向量：df，df=[cosθfsinθf]。

其中，下標s 表示起始位置的參數，f 表示終止位置的參數，θ表示位姿點的方向向量與x軸正方向的夾角。

三維路徑中的參數定義如下：

（1）起始位姿點：ps(xs,ys,zs)。

（2）起始位姿點方向向量：ds(xds,yds,zds)。

（3）終止位姿點：pf(xf,yf,zf)。

（4）終止位姿點方向向量：df(xdf,ydf,zdf)。其余參數定義如下：

（1）起始轉彎圓轉向：turns，其值為1 表示向左轉，為-1 表示向右轉。

（2）起始轉彎圓半徑：rs，其中ks為起始轉彎圓曲率。

（3）終止轉彎圓轉向：turnf，其值為1 表示向左轉，為-1 表示向右轉。

1.2 計算規則

下面對路徑規劃中所涉及的一些變量的計算方法進行講解。

（1）二維平面

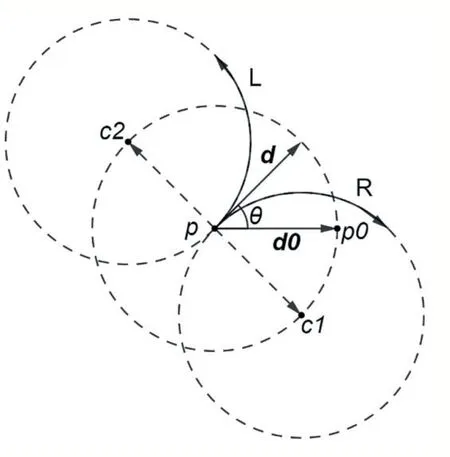
圖1 二維平面上位姿點對應的兩個轉彎圓

根據圖1 可知，位姿點的兩個轉彎圓圓心c1 和c2都在以位姿點p 為圓心的圓上，并且它們在圓p 上的夾角與θ相差是位姿點方向向量d 和向量d0的夾角。二維平面上圓上點坐標的求解方法如式（1）所示，其中ε為點在圓上的夾角，圖1 中p0 是ε等于0時計算出來的點坐標，在二維平面上，向量d0 與x 軸正方向平行且同向，因此d 和d0 的夾角就等于參數中的θ。根據式（1）可知，當ε增大時，計算出來的點在原點的左邊，當ε減小時，計算出來的點在原點的右邊，因此，圖1 中c1 在圓p 上的夾角為在圓p 上的夾角為反過來，p 在圓c1 上的夾角為在圓c2 上的夾角為

定義位姿點p 在轉彎圓上夾角為ε，當點p 向左旋轉v 度后對應的坐標如式（2）所示，當點p 向右旋轉v 度后對應的坐標如式（3）所示。

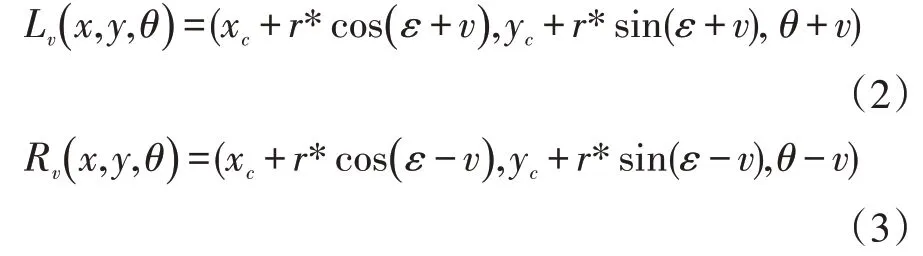
位姿點(x,y,θ)沿當前方向直線前進長度v 后的坐標如式（4）所示。

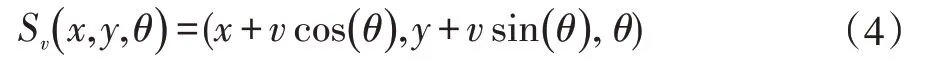
（2）三維平面

三維平面由于其特殊性，需要定義描述圓轉向的視角，若三維平面的法向量指向的是三維坐標軸中負軸的方向，則視線和法向量的指向保持一致，若法向量指向的是三維坐標軸中正軸的方向，則視線和法向量的指向相反。

式（5）是三維平面上圓上點坐標的求解公式。

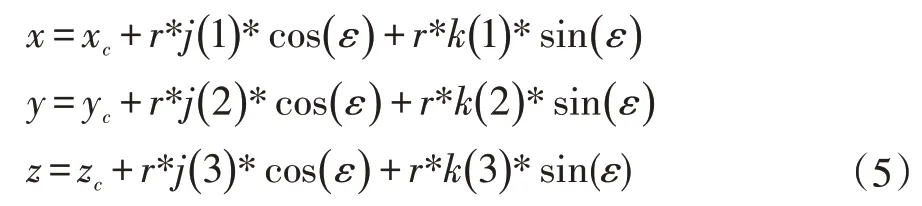
其中，j 和k 的計算方法如式（6）所示。

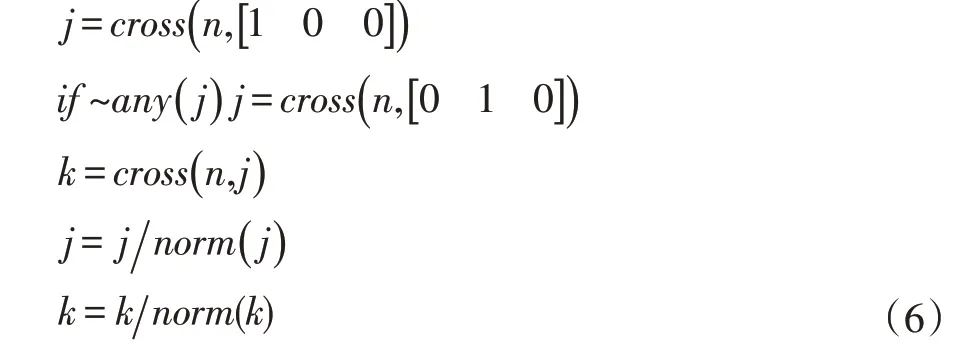
其中，n 是圓所在三維平面的法向量，ε是點在圓上的夾角。根據式（6）可知，三維平面上圓上點坐標的計算公式與三維平面的法向量有關。設點的夾角ε遞增，若法向量n 指向負軸的方向，則根據式（5）、式（6）得到的圓上點向右轉，若法向量n 指向正軸的方向，則根據式（5）、式（6）得到的圓上點向左轉。定義變量dire 來表示法向量n 下根據式（5）、式（6）得到的圓上點的轉向，則dire 的值如式（7）所示，值為1 表示向左轉，為-1 表示向右轉。

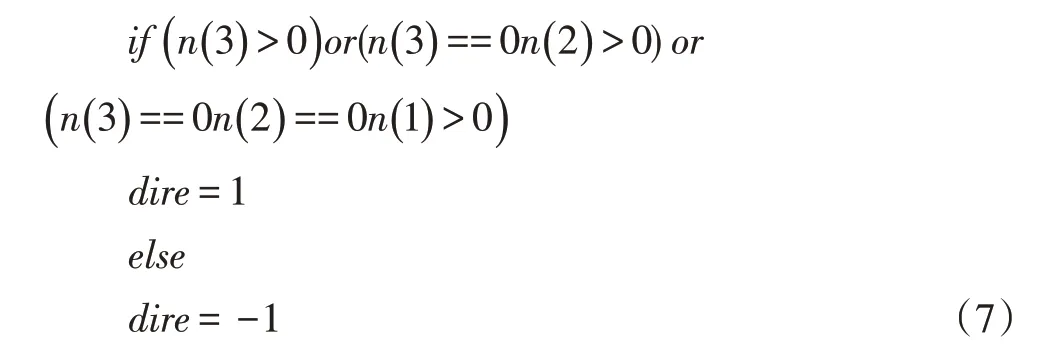
式（7）表示的意思是當法向量中z 坐標值大于0時得到的圓上點向左轉，z 坐標值小于0 時得到的圓上點向右轉，若z 坐標值等于0，則判斷y 坐標的值，y 坐標值大于0 時得到的圓上點向左轉，y 坐標值小于0 時得到的圓上點向右轉，若y 坐標的值也等于0，則再判斷x 坐標的值，判斷方法和前面一樣。

圖2 展示了三維平面上位姿點對應的兩個轉彎圓，可以看到，在三維平面上，位姿點也可以向左轉或向右轉，因此，三維平面上對應的CSC 型Dubins 路徑也有四種子類型，即LSL、LSR、RSL、RSR。

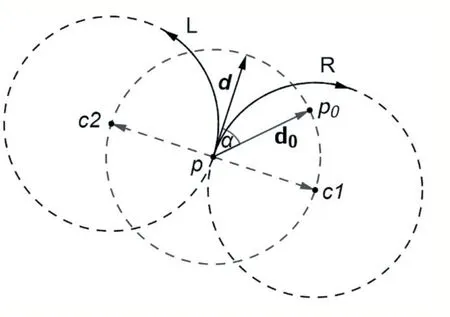
圖2 三維平面上位姿點對應的兩個轉彎圓

圖2 中p0 是圓p 上的起點，即夾角ε為0 時根據式（5）、式（6）計算出來的圓上的點，α是位姿點方向向量d 和向量d0 的夾角。轉彎圓圓心c1 和c2 在圓p上的夾角與α相差，具體的求解方法如式（8）所示。

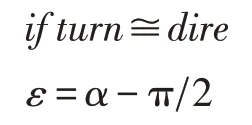
式（8）表達的意思是如果轉彎圓轉向turn 和dire的值不相同，則圓心在圓p 上夾角為如果轉彎圓轉向turn 和dire 的值相同，則圓心在圓p 上夾角為與二維平面相比不同的是，這里還要考慮dire 的值。

三維空間中點(x,y,z)沿單位方向向量[m,n,q]前進長度v 后的坐標如式（9）所示。

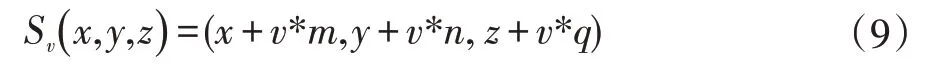
2 計算二維Dubins路徑

圖3 給出了一條二維Dubins 路徑。將Dubins 路徑分成三段，并給每一段設置一個FS 坐標系，分別為起始坐標系es、連接坐標系ec和終止坐標系ef。

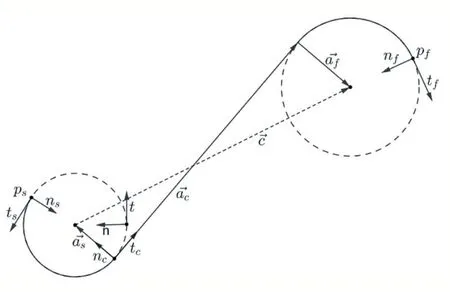
圖3 二維平面上的Dubins路徑

定義基坐標系e[t,n]，則es、ec和ef與e分別有如下關系：

其中，R(θs)、R(φ)、R(θf)表示對應角度下的坐標系的逆時針旋轉矩陣。φ和θs存在如下關系。

當起始轉彎圓向左轉時：

當起始轉彎圓向右轉時：

其中，φs表示起始弧對應的角度。由圖3 可知，二維平面上Dubins 路徑中存在如下的矢量等式：

在基坐標系e 下，矢量c、as、af和ac可寫為如下

形式：

其中c 是中心矢量c 的長度，u 是單位矢量，a 是切向量ac的長度。由圖3 可知，中心矢量c 可由兩個轉彎圓圓心得到。

式（13）可表示為如下形式：

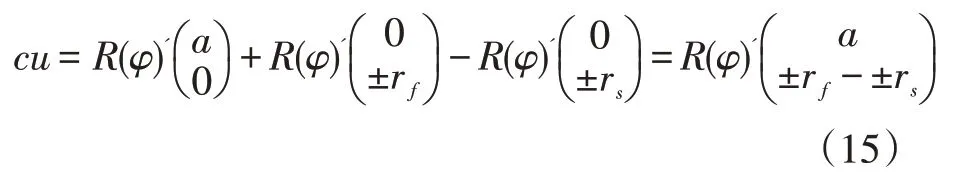
由于上式是一個旋轉等式，因此左右兩邊的矢量幅值應相等：

所以，a 可以表達為：

其中，半徑的正負號和轉彎圓的轉向有關，具體的對照關系可以查看表1。

表1 與路徑類型對應的a 的計算公式

為了計算φ，式（15）可以寫為如下形式：

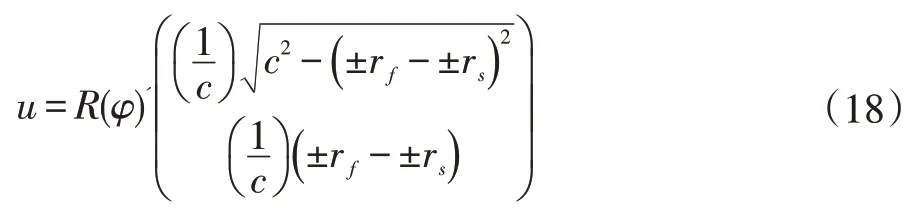
其中

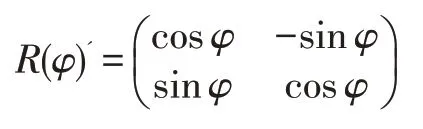
進而解出φ：

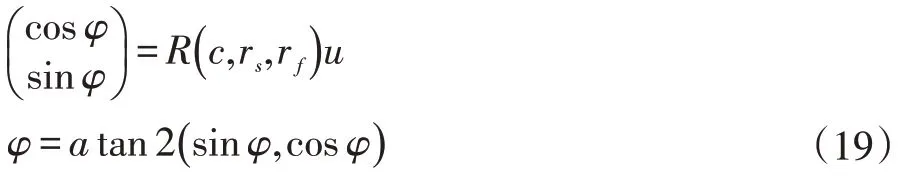
其中：

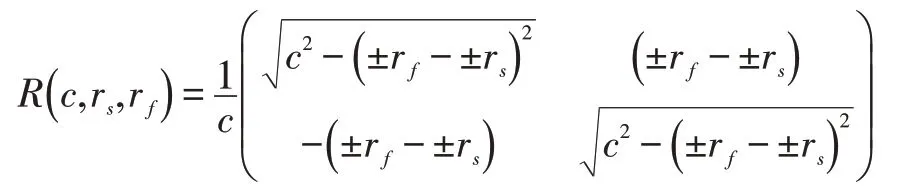
解出φ后就可以根據起始轉彎圓的轉向和式（11）、式（12）解出φs，得到φs的值后要進行如式（20）所示的取模運算，然后根據表2 即可求出終止弧對應的角度φf，得到φf的值后也要進行如式（21）所示的取模運算。

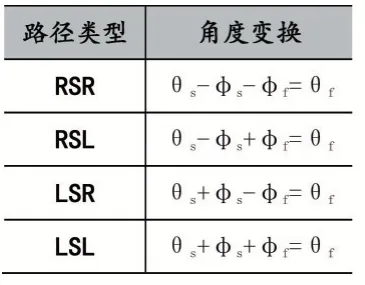
表2 路徑類型與角度變換關系

到此，Dubins 路徑的三個關鍵信息—起始弧對應的角度φs、切線段的長度a以及終止弧對應的角度φf都得到了，根據所需要的路徑上點的個數、Dubins 路徑的子類型以及式（2）、式（3）、式（4）便可以求得路徑上點的坐標。

3 計算三維Dubins路徑

求解三維Dubins 路徑的主要思路是先將起始位姿點旋轉到與終止位姿點共面的位置，然后求解三維平面上的Dubins 路徑，最后將旋轉路徑和平面上的Dubins 路徑組合起來構成指定兩點之間的三維Dubins路徑。

（1）旋轉起始位姿點到與終止位姿點共面的位置。使用平行的向量一定共面這個理論來判斷兩位姿點是否共面以及尋找共面位置。圖4 描述了空間中位姿點的轉彎圓，可以看出，在三維空間中，從一個位姿點出發，可以向各個方向以圓的形式旋轉，位姿點最終可以旋轉到空間中任意方向。因此，一定存在一個轉彎圓上的某個點的方向與終止位姿點平行。

根據法向量的定理可知，三維平面的法向量一定與平面上的向量垂直。若平面上的向量與終止位姿點的方向向量平行，則法向量也與終止位姿點的方向向量垂直。由圖4 可知，圓上點的方向就是點的切向量，假設圓pc 是尋找的轉彎圓，可以看到圓心pc 在圓ps上的切向量dc 就是圓pc 所在平面的法向量。dc、dv和ds 相互垂直，因此dc 等于dv 叉乘ds。結合式（5）、式（6）可以把圓心pc 用參數的形式表達出來，根據向量垂直的關系建立等式可以把參數解出來，反帶入就得到pc 和dc 的值。

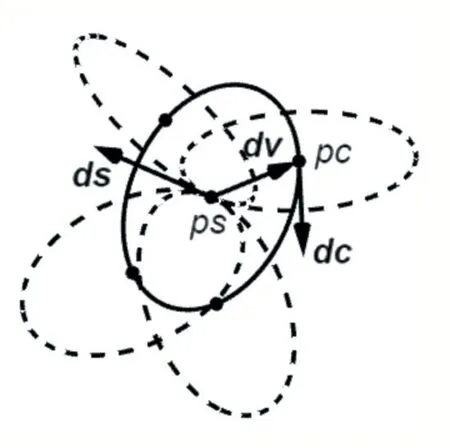
圖4 位姿點的轉彎圓

圖5 是一個三維空間中的Dubins 路徑，可以看到，轉彎圓pc 上存在一點pt，pt 的切向量dt 與終止位姿點的方向df 平行。已知圓心pc 和圓所在平面的法向量dc，則pt 可以根據式（5）、式（6）用參數的形式表達出來。根據向量平行的關系建立等式可以求得參數的解，反帶入就得到pt 和dt 的值，pt 和dt 就構成了和終止位姿點共面的新的起始位姿點。

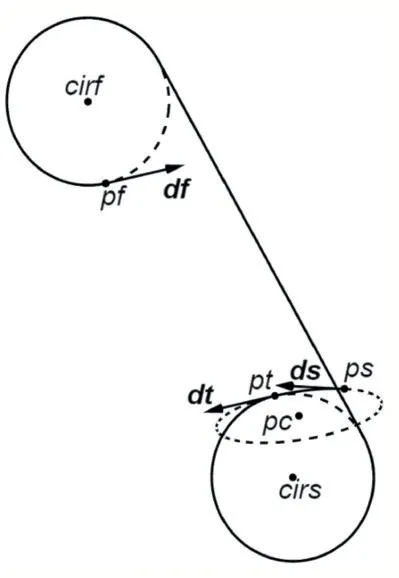
圖5 三維空間中的Dubins路徑

（2）求解三維平面上Dubins 路徑。三維平面上求解Dubins 路徑的原理和步驟與二維平面上一樣，主要是一些變量的求解方法存在區別，下面分析如何求解這些變量。

求解單位向量u。u 是二維向量，如果要在三維平面上求u，則要在三維平面上設計一個類似二維的坐標軸。圖6 展示了一種構造三維平面上類二維坐標軸的方法。

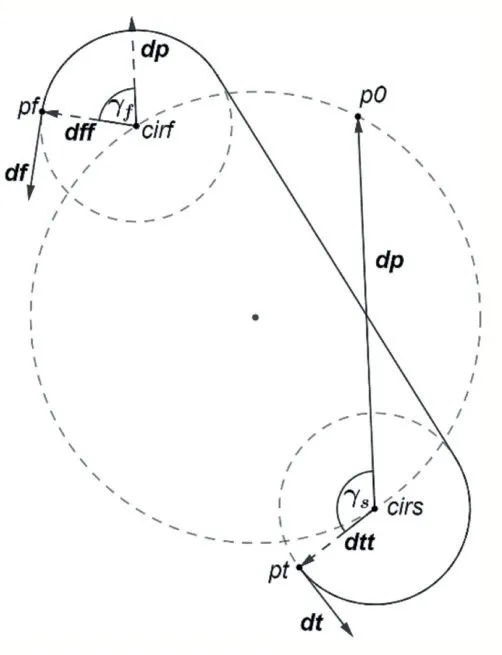
圖6 三維平面上的Dubins路徑

以Dubins 路徑中兩個轉彎圓圓心cirs 和cirf 連線的中點為圓心，作過cirs 和cirf 的圓，找到圓上的起點p0，當出現如下情況時，要對p0 進行一個變換。

式（22）表達的含義是如果p0 在圓心連線的右邊，則將p0 轉換到圓心連線的左邊。連接cirs 和p0 的向量dp 就是類二維坐標系中的x 軸，將dp 向左旋轉就得到了y 軸。因此，三維平面上u 的求解方法如式（23）所示。

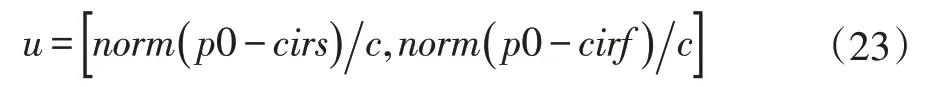
求解對應二維平面上的θs和θf。對應二維平面上的θs和θf的計算方法如表3 所示。

表3 對應二維平面上的θs 和θf 的計算規則

其中γs和γf分別等于從dp 旋轉到dtt、dff 的夾角。這里要注意向量之間旋轉的方向，定義從dp 旋轉到dtt、dff 的旋轉方向為dirc，則dirc 的值如式（24）所示，值為1 表示向左轉，為-1 表示向右轉。

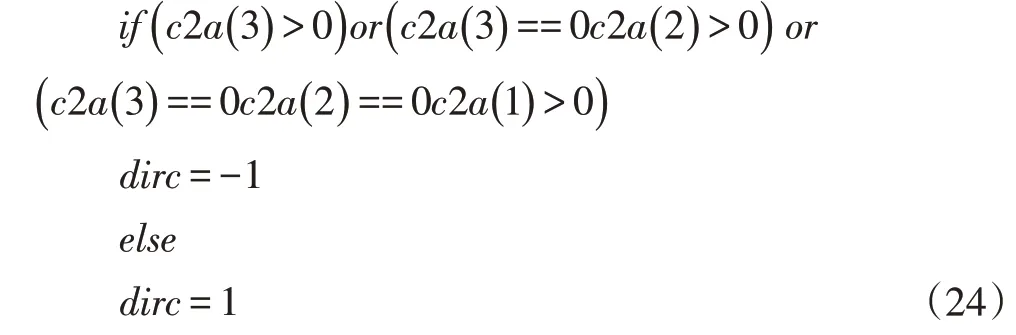
其中c2a 來自于式（22）。要注意，類似判斷條件下式（24）得到的值和式（7）是不一樣的。

以上就是三維平面上相比二維平面計算方法中主要存在差異的變量。到此，根據二維Dubins 路徑的計算步驟就可以求得三維平面上Dubins 路徑起始弧對應的角度φs、切線段的長度a以及終止弧對應的角度φf。起始旋轉弧對應的角度可以通過求解兩個向量之間夾角的方式得到。結合起始旋轉弧段和三維平面上Dubins 路徑就得到了最終的三維Dubins 路徑。根據所需要的路徑上點的個數、Dubins 路徑的子類型以及式（5）、式（6）、式（8）、式（9）便可以求得路徑上點的坐標。

4 仿真驗證

使用MATLAB 軟件對本文算法的有效性進行仿真驗證。圖7 是二維平面上Dubins 路徑的仿真結果，圖8 是三維空間中Dubins 路徑的仿真結果，可以看到，不論是二維平面還是三維空間，本文算法都能成功計算出指定兩點之間的Dubins 路徑。

5 結語

本文對基于微分幾何實現二維和三維Dubins 路徑的原理和步驟進行了細致的闡述，仿真結果表明，本文提出的方法能夠準確計算出二維平面內和三維空間中兩位姿點間的CSC 型Dubins 路徑。

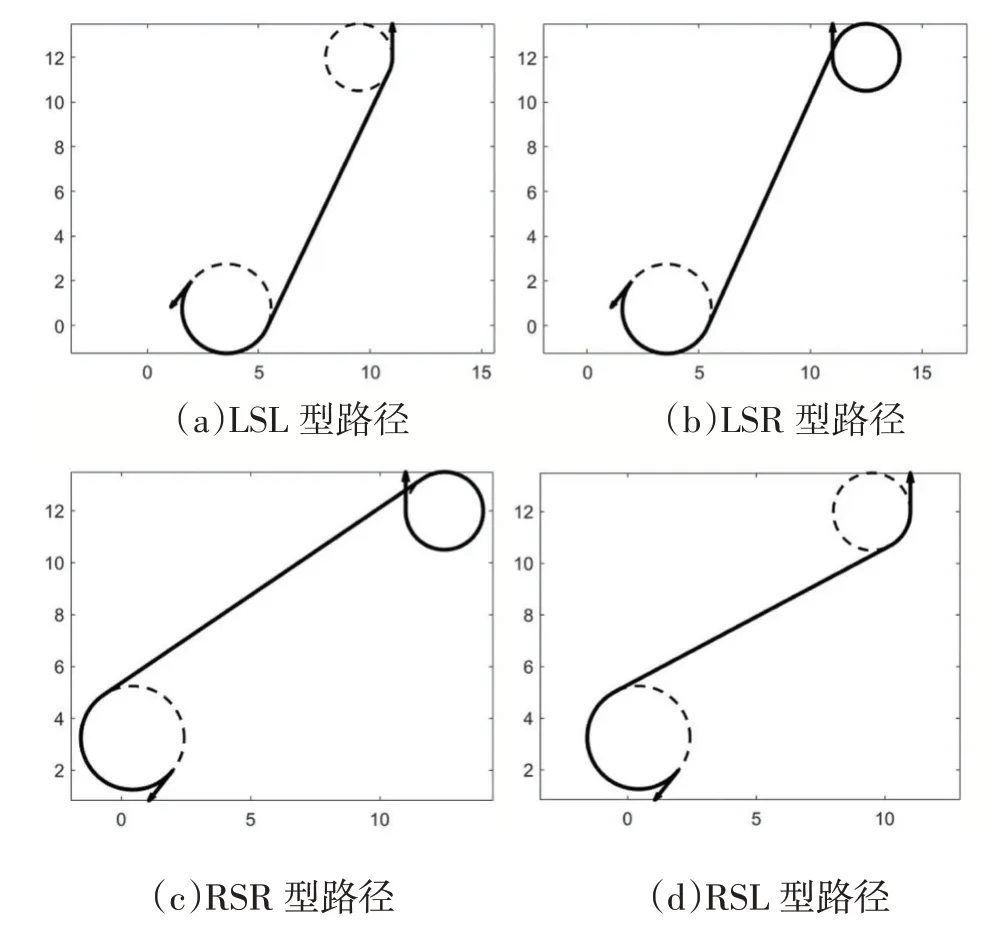
圖7 二維Dubins路徑仿真結果

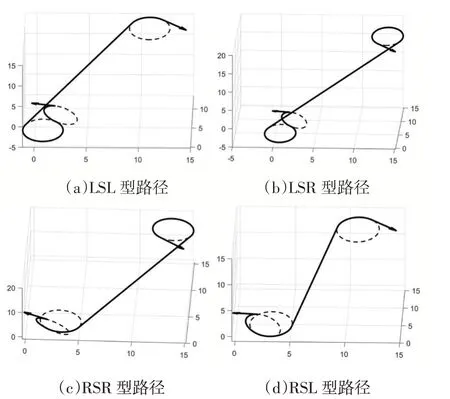
圖8 三維Dubins路徑仿真結果