基于Android的PDR改進算法研究

劉玲玉，劉狄松，常鐵原

(河北大學 電子信息工程學院，河北 保定 071000)

0 引言

自從1992年劍橋大學的Active Badge提出采用紅外傳感技術開發的室內定位系統以來，室內定位技術取得了很大的發展。如采用Wi-Fi[1]、藍牙、ZigBee、超聲 波[2]、超寬 帶[3](UWB)、RFID[4]、慣性 導航等技術[5]實現的室內定位系統也相繼出現，但是至今還沒有一款普遍適用的室內定位產品出現，為此相關學者與研究機構都在努力完善室內定位技術這一局限。近年來由于智能手機技術的進步與普及，基于Android的室內定位也成為了一個焦點，本文利用智能手機內置的傳感器(如加速度傳感器、磁場傳感器)來實現PDR算法，進而實現室內定位，同時，為了提高PDR算法的定位精度，對PDR算法做了優化，主要采用卡爾曼濾波和粒子濾波算法，以及本文提出的直線判定這一方法。

1 PDR算法

PDR算法的實現主要包括三部分，即步數檢測、步長檢測、航向檢測。本文采用改進的峰值檢測法來進行步數檢測，采用步長的經驗模型來進行步長檢測，航向檢測則采用Android提供的方法進行獲取。具體算法如下：

(1)步數檢測

行人在行走過程中其自身的加速度具有周期性[6]，因此，可以根據這一特性進行步數檢測。本文實際測試的行走過程中手持的智能手機的三軸合加速度在7.5～12.5 m/s2之間，實際編程時為了獲取充足的樣本數據將算法中的合加速的的篩選閾值設定為[g，3g](其中 g=9.81 m/s2)，同時為了減少因身體抖動帶來的偽波峰的影響，設定峰值之間的時間間隔要滿足[0.4 s，1 s](之所以設定為該區間，是因為行人的步頻通常為 1～2.5 Hz)。智能手機采集三軸合加速度樣本數據只有滿足上述兩個條件，才會判定為一步，這也是本文提出的改進的峰值檢測法的主要思想。

(2)步長檢測

本文采用線性步長模型進行步長檢測，算法表達式如式(1)所示：

其中，l表示步長，單位：m；k、e 為回歸參數；Accmax、Accmin分別為單步周期內的行人加速度最大值與最小值(本文指智能手機三軸合加速度的最值)，單位：m/s2。

通過多次試驗采集行走過程中加速度最值與實際步長均值的樣本數據，再通過MATLAB軟件線性擬合確定式(1)中的參數 k、e，本文最終的步長檢測模型如式(2)所示：

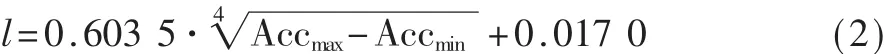
(3)航向檢測

本文的PDR算法是基于智能手機進行開發的，而智能手機中具有多種傳感器能夠實現航向的檢測。之前智能手機中具有單獨的方向傳感器，如今已使用加速度傳感器與磁場傳感器替代。并且Android提供了封裝好的方法用來計算手機的方向角度，如本文采用Android提供的getRotationMatrix()和getOrientation()方法來計算手機頂端與正北方向的夾角。

2 改進的PDR算法

使用PDR算法實現定位時除了其本身產生的累積誤差外，行走過程中產生的波動或者身體的抖動也會對最終的定位結果產生影響。本文為了提高PDR算法的精度和穩定性，提出了兩種優化方案，第一種是通過直線判定的方式來平滑航向數據；第二種方案是使用濾波算法對步長數據和結果進行優化。接下來對這兩種方案進行詳細闡述：

方案一：直線判定

在同一水平面內，人們行走過程中的軌跡大致可分為沿直線行走和曲線行走，其中軌跡為直線時行人的行走狀態相對比較穩定，本文針對這一點對行人的行走軌跡進行判定，如果為直線行走，則對相鄰的航向進行平滑處理，目的是為了減少由于行走過程中身體的抖動對航向帶來的影響，進而使得直線行走時的航向趨于穩定。直線判定的實現步驟如下：

通過實際測試，得知在沿直線行走時（手持手機于胸前，且手機頂端指向前進的方向），手機檢測到的相鄰航向數據之間差值的絕對值不超過15°，因此，如果相鄰的兩個航向數據之間的差值的絕對值小于等于15°，那么采用式(3)對航行數據進行平滑處理，否則，軌跡為曲線，保持航向數據不變。

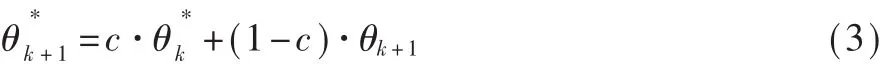
采用上一步中的閾值進行判定時，可能存在突變數據，該突變數據超過了閾值的范圍，但是它又不屬于曲線行走時的航向，為了排除該類數據所帶來的影響，需要對判定為非直線行走的航向數據進一步篩選，篩選算法如下：

如果θk被判定為非直線行走時的航向，那么計算 θk+1與 θk-1之間的差值的絕對值，若該絕對值小于等于 15，那么 θk為突變數據，并且令 θk=θk-1。

方案二：濾波優化

方案一主要針對行走軌跡以直線為主的情形，但實際情況中還有以曲線為主的軌跡，而方案一不適用于該情況。因此，本文提出了濾波優化的方案，主要是針對行走時的步長數據和估算結果進行優化，進而提高PDR算法在軌跡為以曲線為主時的定位精度。采用卡爾曼濾波算法平滑處理步長數據，粒子濾波算法對結果進行優化。

本文將卡爾曼濾波進行了一定的簡化，即令A=B=H=1，U(k)=W(k)=0，Q=0.000 001，R=0.001，同時令X(0)=0，P(0)=1.0，那么公式相關表達式的形式變為：

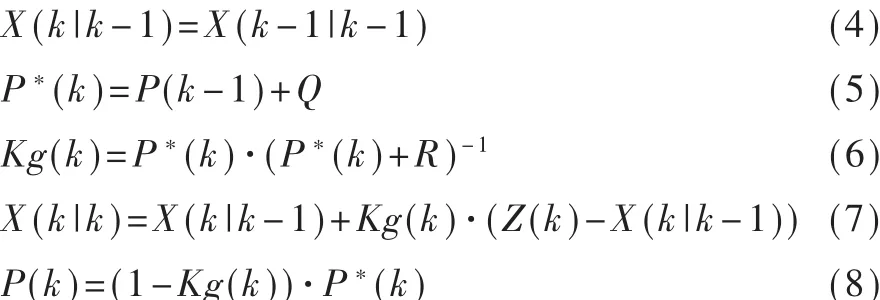
其中，X(k|k-1)表示第k-1時刻對第k時刻的狀態的預測值；X(k-1|k-1)表示第k-1時刻修正過的狀態的估計值；P(k)表示第k時刻狀態估計值與真實值的協方差；P*(k)表示第k時刻狀態預測值與真實值的協方差；Kg(k)表示第k時刻的卡爾曼增益參數；X(k|k)表示第k的狀態估計值。

通過式(4)～式(8)對步長數據平滑處理，再通過平滑后的步長數據估算行人的位置坐標。

粒子濾波優化的基本思想是：首先，以前一個PDR估算的位置為中心，在半徑為 radius(單位：m)的范圍內以任意的角度生成N個點，這N個點稱之為粒子，將它們的初始權重設置為1/N，接著這些粒子按下一個位置的步長和航向運動，最后將運動后的粒子群中的粒子與PDR的估算的下一個位置進行比較，并按歐式距離的大小更新粒子的權重，所有粒子的位置坐標的加權和即為最終的優化結果。

本文結果優化是在步長優化后的基礎上進行的，相關的算法模型如式（9）～式（15）所示。

粒子初始化方程：

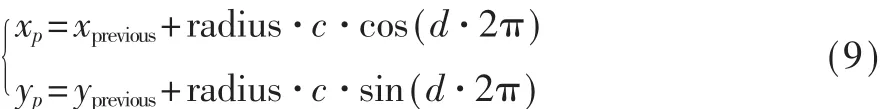
其中，(xp，yp)表示某一個粒子的位置坐標；(xprevious，yprevious)表示PDR估算的行人的前一個位置的坐標；radius表示半徑，為一個常數；c、d表示隨機生成隨機數，本文取0到1之間的浮點型數值。

粒子運動方程：

其中，(xlater，ylater)表示運動后的粒子位置坐標；llater表示PDR檢測的下一個位置處的步長；θlater表示PDR檢測的下一個位置處的航向。

權重更新方程：

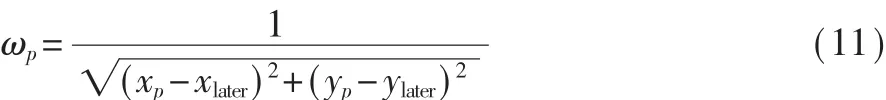
其中，ωp表示更新后的粒子權重；(xlater，ylater)表示 PDR估算的行人下一個位置的坐標。

歸一化處理：

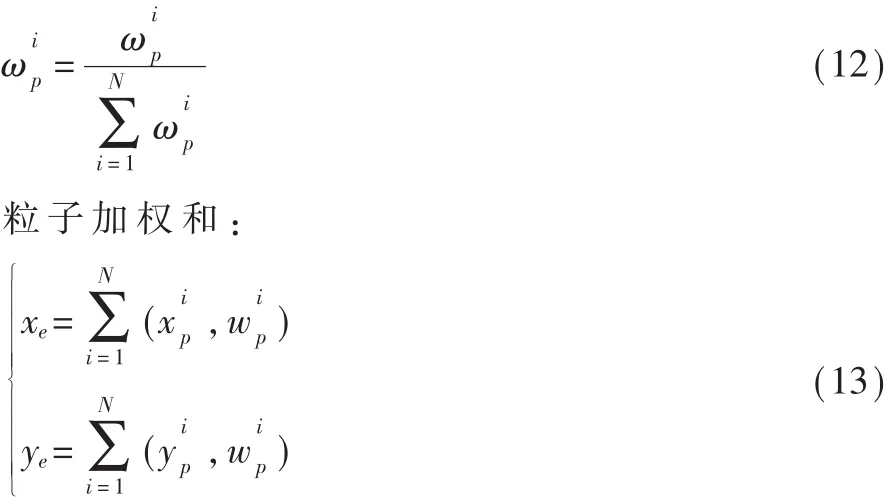
其中，(xe，ye)表示粒子加權后的位置坐標；N表示粒子的個數；()表示第 i個粒子的位置坐標；ωip表示第i個粒子的權重。

重采樣：本文所得的最終優化的結果是經過多次迭代后的均值，每次迭代為一次粒子濾波過程，同時產生一個加權和，即如果總共進行n次迭代，那么將產生 n個加權和(由式(13)計算所得)，將這 n個加權和的平均值作為最終的優化結果。但是為了保證每次迭代后的結果的多樣性，需要對粒子群中的N個粒子進行更新，即重采樣。本文采用如下方法實現重采樣，主要思想是：對于粒子群中的N個粒子，經過一次迭代后，其權重根據與PDR估算的位置坐標的距離進行更新，如式(11)所示，再通過式(12)、式(13)獲得一個加權和，之后需要對粒子進行更新(也叫重采樣)，為下一次迭代做準備。重采樣的數學相關表達式如式(14)～式(16)所示：

初始時，令num=0，r=N(N表示粒子的個數)

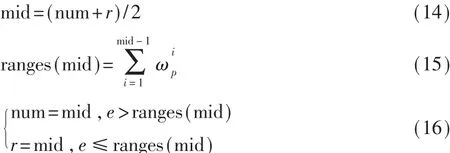
其中，ranges(0)=0，ranges(mid)表示從第 1個粒子到第mid個粒子的權重之和；e為隨機生成的一個浮點型數據，且 e∈(0，1)。

按式(14)～式(16)實現二分法，直到 num+1≥r，此時將第num個粒子根據式(9)進行重采樣，并將它的權重設置為1/N。如此循環N次，即可完成粒子的重采樣。

3 實驗與分析

為了測試算法的效果，本文選定河北大學工商學院的C2樓的第三層的走廊為實驗測試的場所，主要分為兩種場景進行測試：直線為主的軌跡和曲線為主的軌跡。兩種軌跡的初始位置坐標都設置為(0，0)，其中粒子濾波的迭代次數設置為 70次，半徑radius=3 m，粒子數N=200。兩種場景的測試軌跡圖分別如圖1和圖2所示。

從圖1中可知采用直線判定平滑的估計軌跡在軌跡的直線部分更加接近實際軌跡，并且直線判定平滑后，軌跡誤差從2.46 m降低為0.64 m；從圖 2可知，采用卡爾曼濾波平滑處理步長數據和粒子濾波優化結果同樣能夠使得估算軌跡更加接近實際軌跡，其中PDR算法的估算軌跡誤差為6.20 m，采用卡爾曼濾波平滑處理步長數據后的誤差降為1.67 m，在卡爾曼濾波的基礎上采用粒子濾波優化結果的軌跡誤差降為1.08 m。本文的誤差采用公式（17）計算所得：

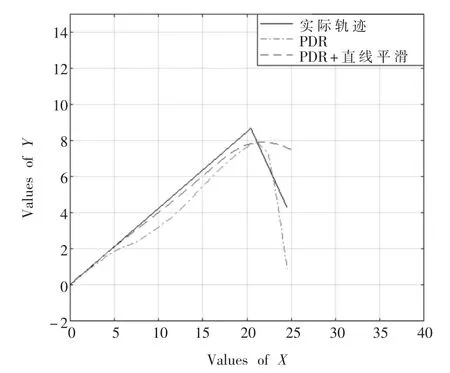
圖1 直線為主的軌跡

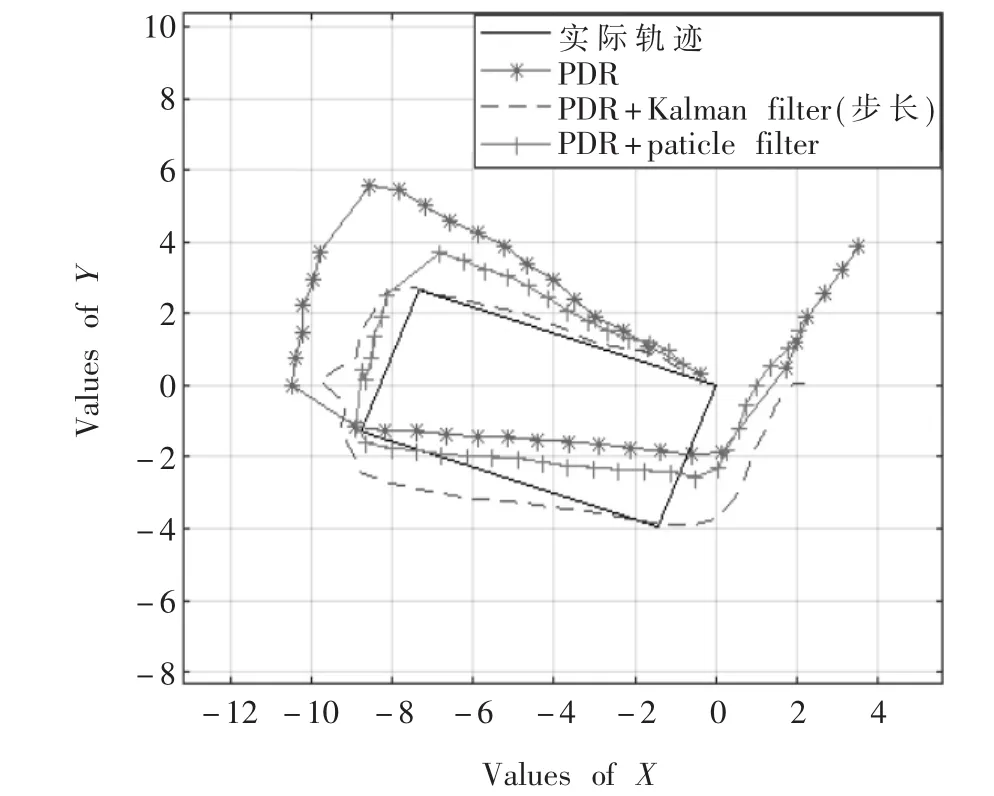
圖2 曲線為主的軌跡

其中，(x，y)表示定位坐標，(x0，y0)表示實際坐標。

4 結論

本文提出的針對兩種場景 (直線為主的軌跡、曲線為主的軌跡)下的優化方案能夠提高PDR算法的精度，具有一定的使用價值。但是PDR算法所得結果都是相對的，即需要一個初始的參考位置，在實際應用中需要加以解決。如與基于Wi-Fi或者藍牙的指紋法相結合，指紋法能夠提供初始的參考位置或者校準PDR算法的累積誤差。除此外，還可以與其他技術相結合進行融合定位，如地圖匹配、濾波融合等，這也是之后的一些可供參考的研究方向。