增值評價中缺失數據對線性回歸模型成績預測的影響

徐路明 楊亞坤

一、問題提出

教育質量評價僅以終結性評價為標準對于不同學校群體有失公允，對學校的教學積極性也是不利的，需要更加科學和準確地評價學校和教師的效能。《教育部關于推進中小學教育質量綜合評價改革的意見》中提出要改進評價方式方法，要通過直接考查學生群體的發展情況評價學校的教育質量，注重考查學生進步的程度和學校的努力程度，改變單純強調結果不關注發展變化的做法[1]；《中共中央國務院關于深化教育教學改革全面提高義務教育質量的意見》中再一次強調了要健全質量評價監測體系，強化過程性和發展性評價[2]。《溫州市中小學教育質量增值評價實施指導意見》中提出，要關注評價的起點和過程，切實解決因起跑線不同帶來的評價偏差[3]。基于此，一些地區在對學校的教學質量評價中引入了增值評價，以學校為單位，用以判斷教學質量的提升程度。學校效能增值性評價的出現源于美國《關于教育機會平等性的報告》[4]。增值評價是指通過追蹤研究設計，收集學生在一段時間內不同時間點上的標準化測驗成績，基于學生自身測驗成績的縱向比較，并考慮其他不受學校或教師控制因素對學生成績的影響 （如學生的原有成績水平、人口學因素、家庭背景信息以及學校周圍地區的經濟發展水平等）[5]。

增值性評價作為關注學生自身進步與發展的一種方法，不同于以往的終結性評價，也不單單是對學業質量進行一個橫向的比較，它是實現發展性評價的重要手段之一。現有的增值評價研究包括對國際上增值評價的介紹，例如，徐丹和牛月蕾就對美國田納西州的教育增值評價模式進行了介紹[6]。也有學者運用多水平分析模型對學校效能進行增值評價，如杜屏和楊中超運用兩水平模型對農村初中學校的效能進行增值評價，探討了學生水平、學校水平對學校效能的解釋力[7]。馬曉強、彭文蓉和薩麗·托馬斯運用增值評價對河北保定市高中學校進行效能判斷，研究發現60%～80%的高考成績校際差距都不是學校教育教學差異所導致的， 生源、學生背景、學校背景解釋了絕大多數的差異，在提高學生進步幅度方面，不同學校間存在明顯差異[8]。大學時期增值評價的研究在評價內容、方法上則更為復雜，學生在大學期間增值的維度較多，關鍵維度和指標的選取及測試方法的操作性、應用性有待進一步完善[9]。除了一般統計模型方法，楊志明、賈立新和呂龍梅還將心理等值的技術運用到增值評價中，從而更好地對閱讀能力進行評價[10]。 王光秋在四維綠色評價體系中引入了增值評價[11]。

可以看到，增值評價的研究與應用都在不斷豐富，在應用的學段上，既有義務教育階段的，也有高中、高等教育階段的；在運用的模型上，既有概要分析、一元回歸分析、多元回歸分析，也有多水平分析模型；在評價維度上，既有基于學業的一元增值評價，也有包括學業、品德、身心健康等的多元評價。

然而，在基層（區、縣）實際應用中，在對學校學業成績增值情況進行評價時，由于學生轉學、回生源地參加中、高考等原因導致區域、學校層面的入口出口數據不完整，在不能把全區（縣）所有的學生都納入建模樣本時，用構建后的模型進行成績預測的可靠性如何，每個學校運用該模型進行成績預測的誤差如何？研究表明，當缺失值的比例超過60%時，數據完全失去了可利用的價值[12]。 在對學校的學業成績進行預測時，缺失比例達到多少會對學校最后的增值排名產生影響？ 在不同的樣本量下，上述情況又會有何不同呢？區域內學校水平分布是否會對學校增值產生影響？

本研究使用線性回歸模型來構建學生入學成績和畢業成績的關系，以學校為單位，用入學成績來預測其畢業成績，將預期值與實際畢業成績相減得到每個學校的增量，如圖1 所示。線性回歸分析包括一元線性回歸分析和多元線性回歸分析等，它是一個因變量與一個或多個自變量之間的線性關系常用的統計方法，這一方法是估計觀測值與期望值之間殘差值的標準統計技術[13]。 在基層（區、縣）評價機構或教學一線使用時，一元線性回歸模型原理通俗易懂，更容易被理解、接受，且區（縣）層面樣本量相對市、省級小，缺失數據對其影響更大，故本研究選用一元線性回歸模型作為研究載體。

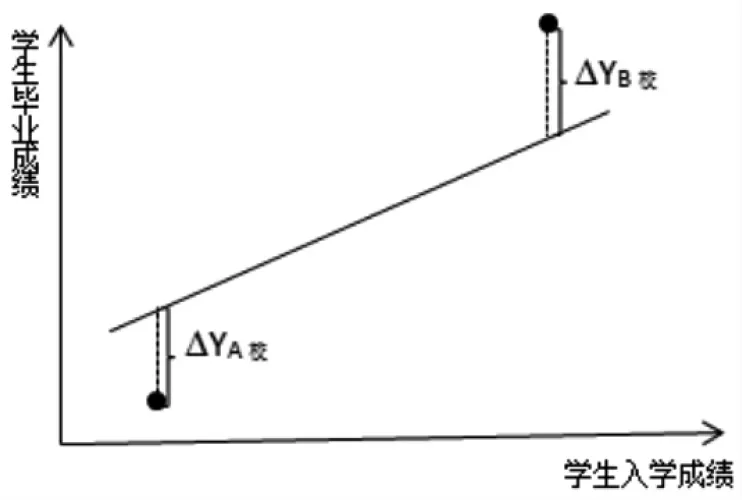
圖1 學校增值情況線性回歸模型

二、模擬研究

1.研究目的

本研究擬通過設定不同的缺失比例，比較不同樣本量大小和學生入學成績是否存在差異等因素對學校增值效能排名的影響。

2.研究方法

本研究為4×3×2 的混合設計，缺失比例設置4個水平：5%、10%、30%、60%， 樣本量設置3 個水平：2000 人、5000 人、10000 人， 學校設置兩個水平：均衡（即不同學校學生成績隨機生成）、不均衡（即不同學校學生入學成績按從小到大排序生成）。其中，學校水平差異為被試內變量，缺失比例、樣本量為被試間變量，學校數量固定為20 所。

本研究為模擬研究，通過mvrnorm 函數生成服從多元正態分布的兩列數據，兩列數據的相關系數r 為0.9，均值為70，標準差為15，并在此數據的基礎上隨機缺失1000 次。

3.評價指標

結果分析指標包括學校排名變化總量、排名變化量/校、整體回歸系數的ABS、SD 值。完整的數據集和缺失的數據集里每個學校的增值量均可計算，根據增量每個學校會獲得一個名次，排名變化總量為所有學校在完整、缺失兩種情況下相差名次的總和； 排名變化量/校指排名變化總量與發生排名變化的學校數量之比， 上述兩個指標均為隨機缺失1000 次結果的均值；整體回歸系數的ABS、SD 值計算公式如下（以A 系數為例），N 為1000 次：

三、研究結果

1.缺失比例與樣本量對學校排名的影響

表1 和表2 分別呈現了不同學校水平分布下，缺失比例和樣本人數對學校增值排名的影響。從表1 可以看出，在學校水平均衡時，缺失比例與樣本量均對學校排名變化有影響。當缺失比例從5%增加到60%時，學校排名變化總量從2 個名次上升到6 個名次，平均每所學校的排名變化從0.63 個上升到1.40 個名次，均在1 個名次左右。在不同的缺失比例下，隨著樣本量的增加，學校排名變化總量和每所學校排名變化量均呈現下降的趨勢。

表1 缺失比例與樣本量對學校排名的影響（學校水平均衡）

從表2 可以看出，當學校水平不均衡時，隨著缺失比例的增加，學校排名變化總量和每所學校排名變化量仍呈遞增的趨勢。當缺失比例從5%增加到60%時， 學校排名變化總量從5 名增加到12名，且每所學校排名變化均量從1 名增加到2 名；但樣本量的影響不太明顯。 相比學生入學成績無差異，此時排名變化總量和每所學校排名變化量有所增加。

表2 缺失比例與樣本量對學校排名的影響（學校水平不均衡）

2.缺失比例與樣本量對回歸系數的影響

表3 和表4 分別呈現了不同學校水平分布下，缺失比例和樣本人數對回歸系數返真性、穩健性的影響。從表3 可以看出，隨著缺失比例增加，在學校水平均衡時，回歸方程的A 和B 值在ABS 和SD 指標上呈現出遞增的趨勢，A 值的ABS 值從0.0008增加到0.0091，SD 值從0.0006 增加到0.0071；隨著樣本量增加，A、B 值的ABS 和SD 指標呈現出遞減的趨勢。

從表4 可以看出，當學校水平不均衡時，隨著缺失比例和樣本量的改變，A 和B 系數的ABS 和SD 指標的大小與學校水平均衡時相差不大， 且呈現出與學校水平均衡時相同的變化趨勢。

表3 缺失比例與樣本量對回歸方程的影響（學校水平均衡）

表4 缺失比例與樣本量對回歸方程的影響（學校水平不均衡）

四、討論

1.缺失比例對學校增值的影響

在學校水平均衡時，隨著缺失比例的增加，學校增值評價排名的誤差也逐漸增加。缺失比例的增加會使得可獲得的數據信息減少，從而使得回歸線越來越偏離真實回歸線。在學校水平均衡時，隨著缺失比例的增加，學校平均名次變化維持在1 名左右，但學校排名變化總量呈現遞增的趨勢。當缺失比例為5%時，學校排名變化總量為2 名左右，當缺失比例上升到10%時， 學校排名變化總量變化不大。 若區域內學校水平相差不大， 且缺失比例在5%、10%左右時，可考慮繼續使用增值評價。 當缺失比例繼續上升到30%、60%時， 學校排名變化總量上升到4 名、6 名左右，誤差相對來說增大。

在學校水平不均衡時，學校增值的誤差相對學校水平均衡時增加。 但就回歸系數而言，在某一固定缺失比例下，學校水平是否均衡對于整體的回歸系數影響不大。 這可能是因為在學校水平均衡時，每個學校都是總體的一個代表性樣本，學校回歸系數與整體回歸系數差異較小； 而學校水平不均衡時，每個學校學生成績分布較為集中，學校回歸系數與整體回歸系數差異較大，故在學校水平不均衡時，學校增值誤差相對較大。隨著缺失比例的增加，平均每校名次變化和學校排名變化總量也呈現出遞增的趨勢。當缺失比例為5%時，學校排名變化總量為5 名左右，平均每校名次變化為1 名；當缺失比例為10%時，學校排名變化總量變化不大，為6名，平均每校名次變化仍為1 名。 若區域內學校水平相差較大，且缺失比例在5%、10%左右時，可根據區域實際情況來判斷是否繼續使用增值評價。當缺失比例繼續上升為30%、60%時， 學校名次變化總量和平均每校名次變化量增加較多，學校名次變化總量分別為9 名、12 名，平均每校名次變化均為2 名左右。

2.樣本量對學校增值的影響

隨著樣本量的增加，學校增值評價排名的誤差呈遞減的趨勢，但這種趨勢在學校水平不均衡時并不明顯。總體來講，樣本量對學校增值評價排名有一定的影響，因為在相同缺失比例下，學生數量的增加會使得計算獲得的信息增加， 但這種影響較小。如當學校水平均衡、缺失比例為5%時，當樣本量從2000 增加到10000， 學校排名變化總量從2.48 名下降到1.52 名， 但仍然維持在2 名左右，學校排名變化/校從0.77 名下降到0.63 名； 缺失比例為10%時， 學校排名變化總量從2.55 名下降到2.32 名， 誤差量沒有像缺失比例那樣發生質的變化。

五、結語

總而言之，樣本量、缺失比例、學校水平分布均會對最終學校的增值情況產生影響。學校水平不均衡時，相同條件下，誤差會大于學校水平均衡時的情況。樣本量在2000-10000 之間時，不同的樣本量影響不大。 區域缺失比例在5%、10%左右時，結果如上所示，相對來說誤差不大，尚可接受，但各區域需按照本區域的實際情況與誤差情況接受度，來做出相應的判斷和決定。