基于項(xiàng)目類別的多級(jí)評(píng)分方式比較及探究
朱仕浩 康春花 洪清玉
一、引言
認(rèn)知診斷(Cognitive Diagnosis,CD)是指對(duì)個(gè)體認(rèn)知過程、加工技能或知識(shí)結(jié)構(gòu)的診斷評(píng)價(jià)[1]。它能夠探討個(gè)體內(nèi)部的心理加工機(jī)制,實(shí)現(xiàn)對(duì)個(gè)體認(rèn)知發(fā)展實(shí)況的診斷評(píng)估。在認(rèn)知診斷評(píng)分方式上,現(xiàn)多以Q 矩陣為基礎(chǔ),實(shí)現(xiàn)以題目對(duì)錯(cuò)為判別的0-1 評(píng)分,以及多級(jí)評(píng)分。與0-1 評(píng)分相比,多級(jí)評(píng)分可以提供更多的被試診斷信息,因而被廣泛使用。
現(xiàn)有多級(jí)評(píng)分的認(rèn)知診斷方法大多在Q 矩陣基礎(chǔ)上架構(gòu),根據(jù)是否需要參數(shù)估計(jì)可將認(rèn)知診斷方法分為參數(shù)方法和非參數(shù)方法[2]。參數(shù)方法已有研究有祝玉芳、 丁樹良開發(fā)多級(jí)評(píng)分的AHM,Templin、Henson、Rupp、Jang 和Ahmed 提出的稱名反應(yīng)診斷模型,涂冬波、蔡艷、戴海琦、丁樹良開發(fā)的多級(jí)評(píng)分PDINA 模型,Hansen 提出的等級(jí)反應(yīng)LCDM 等[3-6]。在非參數(shù)方法上, 也有Sun、Xin、Zhang 和de la Torre的拓展多級(jí)的廣義距離判別法,康春花、任平、曾平飛開發(fā)的多級(jí)評(píng)分聚類分析,楊亞坤開發(fā)的曼哈頓距 離 判 別 法 (Manhattan distance discrimina tion,MDD)等[7-9]。在這兩類方法中,參數(shù)方法可以通過參數(shù)估計(jì)獲得項(xiàng)目參數(shù),為進(jìn)一步的測驗(yàn)編制或等值提供有用信息,但需要較長時(shí)間和足夠大的樣本量,并且參數(shù)模型選擇困難[10,11]。而非參數(shù)方法作為參數(shù)方法的替代方案用于被試知識(shí)狀態(tài)的判別,擁有判準(zhǔn)率較高、無需進(jìn)行參數(shù)估計(jì)、條件假設(shè)少、受樣本量的影響較小等特點(diǎn)[12]。
這兩類多級(jí)評(píng)分認(rèn)知診斷方法都基于Q 矩陣,并未考慮屬性與項(xiàng)目類別之間的關(guān)系,因而可能會(huì)丟失部分項(xiàng)目信息并影響診斷結(jié)果。對(duì)此,Ma 和de la Torre 在連續(xù)比鏈接函數(shù)基礎(chǔ)上對(duì)CDMs 進(jìn)行拓廣,并將GDINA 模型作為加工函數(shù)(Processing Function),提出了序列加工的seq-GDINA 模型(Sequential GDINA model)。為充分挖掘項(xiàng)目信息,Ma 等同時(shí)定義了一種基于項(xiàng)目類別(item category)的屬性定義法,將傳統(tǒng)的Q 矩陣發(fā)展為基于項(xiàng)目類別的QC 矩陣(a category-level Q-matrix),并借以QC 矩陣提出一種基于項(xiàng)目類別的多級(jí)評(píng)分方法,為多級(jí)評(píng)分提供了新的視角[13,14]。其中的項(xiàng)目類別是指被試作答項(xiàng)目可能出現(xiàn)的情況,例如表1,該項(xiàng)目分兩個(gè)步驟,被試作答可能有3 種:全錯(cuò)、答對(duì)第一步、答對(duì)兩步,所以該項(xiàng)目類別有3 類。與以往的Q 矩陣評(píng)分方式不同,QC 矩陣評(píng)分方式為按項(xiàng)目類別給分,項(xiàng)目過程具有有限多個(gè)步驟,每個(gè)步驟考察一些屬性,最后根據(jù)被試所處項(xiàng)目類別給予相對(duì)應(yīng)的分?jǐn)?shù)。現(xiàn)有QC 矩陣評(píng)分方式嚴(yán)格按步驟順序評(píng)分,即前一步正確作答是后一步的前提,而在實(shí)際應(yīng)用中,學(xué)生很可能并未掌握前一步的屬性,但后一步的屬性卻掌握了,對(duì)于這種情況該評(píng)分方式會(huì)出現(xiàn)誤判。以表1項(xiàng)目為例,假設(shè)某被試在作答該項(xiàng)目時(shí),第一步運(yùn)算結(jié)果為180÷9(正確作答應(yīng)該是180÷10),即第一步計(jì)算錯(cuò)誤,而第二步的運(yùn)算結(jié)果為20(正確作答是18),雖然最終答案與標(biāo)準(zhǔn)答案不同,但第二步考查的屬性該被試已經(jīng)掌握,故應(yīng)當(dāng)給分。 當(dāng)使用順序評(píng)分方式時(shí),該被試得0 分,而如果考慮這種情況,該被試應(yīng)得1 分。綜上所述,現(xiàn)有的QC 矩陣評(píng)分方式未考慮按步驟的非順序評(píng)分情景,并且只被應(yīng)用于參數(shù)方法中,在非參數(shù)方法中的有效性并未驗(yàn)證。故本文欲將QC 矩陣評(píng)分方式與非參數(shù)方法相結(jié)合,并在此基礎(chǔ)上提出一種按步驟的非順序評(píng)分方式。

表1 例題對(duì)應(yīng)的屬性
本文將在QC 矩陣框架下,開展以下兩個(gè)研究:(1)通過對(duì)參數(shù)seq-GDINA 模型與非參數(shù)MDD 在不同條件下的比較;以驗(yàn)證QC 矩陣評(píng)分方式在非參數(shù)方法上的適用性。(2)利用MDD 比較順序評(píng)分與非順序評(píng)分在不同條件下的判準(zhǔn)率情況,以驗(yàn)證非順序評(píng)分方式的有效性。
二、基于項(xiàng)目類別的兩種評(píng)分方式介紹
QC 矩陣中順序評(píng)分的規(guī)則要求題目的前一步正確作答是后一步的基礎(chǔ),如表2,以附錄1 第15題為例,該題QC 矩陣為分三個(gè)步驟,可將被試劃為4 個(gè)類別。在順序評(píng)分的模擬研究中,為符合順序評(píng)分規(guī)則,將QC 矩陣轉(zhuǎn)化為順序的QC 矩陣(見附錄2),并在此基礎(chǔ)上進(jìn)行模擬研究。模擬研究首先確定QC 矩陣,然后利用QC 矩陣和所有被試可能的知識(shí)狀態(tài) (Knowledge State,KS)矩陣相乘生成每個(gè)人在每一道題目的每個(gè)步驟上的作答情況,最后根據(jù)學(xué)生在每道題目上正確作答的步驟數(shù)給予其相應(yīng)得分,得到基于QC 矩陣的順序評(píng)分IRP(Ideal Response Pattern,IRP)。
非順序評(píng)分是為了打破QC 矩陣順序評(píng)分的限制。同樣以附錄1 第15 題為例,QC 矩陣為因?yàn)榉琼樞蛟u(píng)分允許項(xiàng)目按步驟非順序評(píng)分,故無需對(duì)QC 矩陣進(jìn)行轉(zhuǎn)化便可進(jìn)行模擬研究,模擬過程與順序評(píng)分相同。
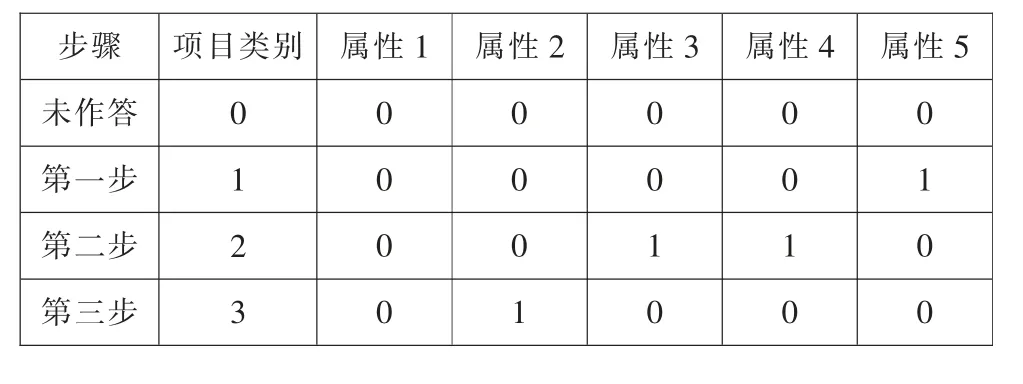
表2 第15 題對(duì)應(yīng)的屬性
三、研究一:非參數(shù)方法(MDD)在QC 矩陣中的應(yīng)用
1.seq-GDINA 模型與MDD 介紹
Ma 和de la Torre 在連續(xù)比鏈接函數(shù)基礎(chǔ)上對(duì)CDMs 進(jìn)行拓廣,并將GDINA 模型作為加工函數(shù),提出了序列加工的seq-GDINA 模型,該模型假設(shè)各步驟是獨(dú)立且繼時(shí)發(fā)生的事件,各事件概率相乘可得最終概率函數(shù)[15]。其表達(dá)式如下:
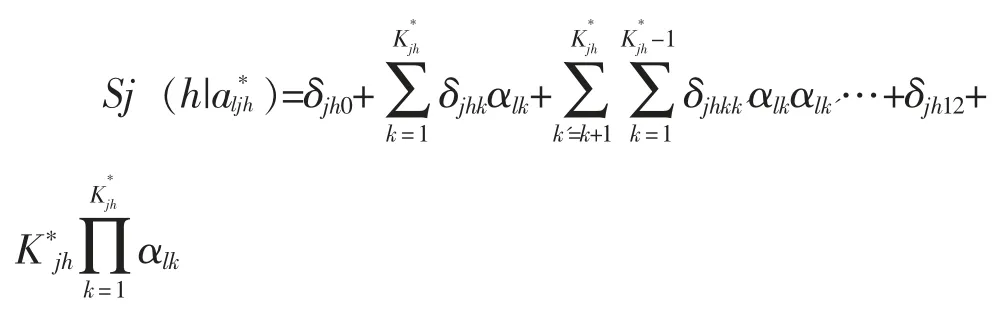
MDD 是楊亞坤基于曼哈頓距離建立起的一種簡單有效的認(rèn)知診斷方法, 由于其不需要參數(shù)計(jì)算所以耗時(shí)極少,該方法計(jì)算公式簡單[16],其表達(dá)式如下:
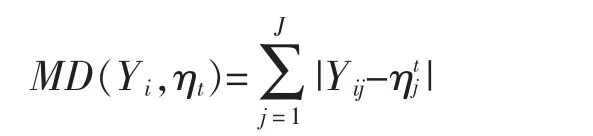
其中Yi表示被試的觀察反應(yīng)模式(Observed Response Pattern,ORP),ηt表示第t 種IRP,Yij為第i個(gè)被試在項(xiàng)目j 上的觀察反應(yīng),為第t 種IRP 在項(xiàng)目j 上的理想反應(yīng)。MD(Yi,ηt)表示為第i 個(gè)被試的ORP 到第t 種IRP 的曼哈頓距離。楊亞坤從數(shù)理上證明這種方法在0-1 計(jì)分情況下與海明距離相同,也就是說海明距離是曼哈頓距離在0-1 計(jì)分情況下的特例。在對(duì)學(xué)生KS 進(jìn)行判別時(shí),MDD 通過計(jì)算學(xué)生的ORP 和IRP 之間的曼哈頓距離實(shí)現(xiàn)對(duì)學(xué)生的分類[17]。
2.seq-GDINA 模型與MDD 在QC 矩陣中的比較
(1)研究目的
本部分通過比較seq-GDINA 模型與MDD 在QC 矩陣中的判準(zhǔn)率,探討QC 矩陣評(píng)分方式在非參數(shù)方法上的適用性,同時(shí)比較在QC 矩陣評(píng)分方式下,參數(shù)方法與非參數(shù)方法在不同條件下的判準(zhǔn)率情況。
(2)實(shí)驗(yàn)設(shè)計(jì)
實(shí)驗(yàn)采用2×3×6 三因素混合實(shí)驗(yàn)設(shè)計(jì),自變量分別:判別方法、項(xiàng)目質(zhì)量和被試人數(shù)。每個(gè)實(shí)驗(yàn)條件重復(fù)進(jìn)行30 次。 采用平均屬性判準(zhǔn)率(Average Attribute Match Ratio,AAMR)和模式判準(zhǔn)率(Pattern Match Ration,PMR) 作為診斷準(zhǔn)確率的評(píng)價(jià)指標(biāo),AAMR 表示所有被試認(rèn)知屬性被判別正確的概率,PMR 表示被判別歸類正確掌握模式的被試個(gè)體占總?cè)藬?shù)的比率,其表達(dá)式分別為:
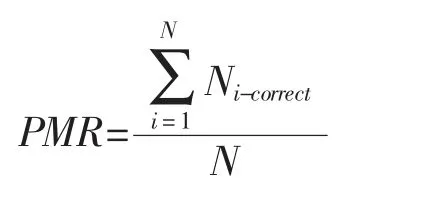
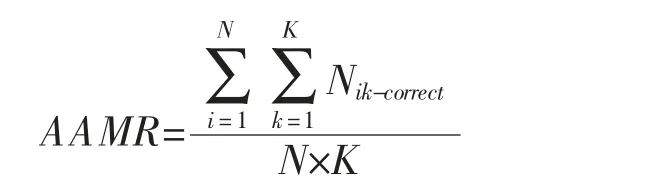
其中,N 表示被試數(shù)目,K 表示屬性個(gè)數(shù),Ni-correct表示第i 個(gè)被試的屬性掌握模式是否被判別準(zhǔn)確,判別正確為1,否則為0。Nik-correct表示被試在認(rèn)知屬性k 上判別正確與否,正確為1,否則為0。從公式中可以發(fā)現(xiàn),PMR 相較于AAMR 能更敏感地反映歸類準(zhǔn)確率。
(3)實(shí)驗(yàn)流程
第一步:確定QC 矩陣,本研究借鑒Ma 等使用的QC 矩陣(詳見附錄1),并將其轉(zhuǎn)化為順序評(píng)分的QC 矩陣[18]。該矩陣包含5 個(gè)屬性,21 題,拆分為步驟后一共40 個(gè)步驟,其中滿分為2 分的項(xiàng)目有13 個(gè),滿分為3 分的項(xiàng)目有3 個(gè),滿分為1 分的項(xiàng)目有5個(gè),所有題目均為按步驟計(jì)分。本研究采用seq-GDINA模型與MDD 兩種方法,模擬被試人數(shù)100、200、300、500、1000、2000 六個(gè)水平,用以比較不同樣本量情況下參數(shù)方法與非參數(shù)方法的判準(zhǔn)率如何變化,并利用張淑梅、包鈺、郭文海提出的滑動(dòng)模擬方法模擬高質(zhì)量(滑動(dòng)概率=0.1)、中質(zhì)量(滑動(dòng)概率=0.2)、低質(zhì)量(滑動(dòng)概率=0.3)三個(gè)水平[19]。屬性層級(jí)結(jié)構(gòu)設(shè)置為獨(dú)立型,評(píng)分方式為QC 矩陣的順序評(píng)分方式。
第二步:根據(jù)屬性個(gè)數(shù)與屬性層級(jí)結(jié)構(gòu)確定所有被試可能的KS,與QC 矩陣相乘,并按步驟累加得到IRP,再模擬作答反應(yīng)數(shù)據(jù),作答反應(yīng)數(shù)據(jù)生成的具體步驟為:首先,產(chǎn)生一個(gè)服從均勻分布U(0,1)的隨機(jī)數(shù)矩陣,維度為N*J,其中N 代表被試數(shù)量,J代表題量。由于前文指出本研究中項(xiàng)目質(zhì)量為高、中、低,即滑動(dòng)概率為0.1、0.2、0.3,利用滑動(dòng)矩陣內(nèi)每個(gè)分?jǐn)?shù)的概率與對(duì)應(yīng)位置rij進(jìn)行比較,根據(jù)滑動(dòng)規(guī)則將不同的rij分別滑動(dòng)到不同的得分,即得到模擬被試的ORP。
第三步:分別利用MDD 與seq-GDINA 模型對(duì)被試的ORP 進(jìn)行判別,并與真值進(jìn)行比較,得到兩個(gè)評(píng)價(jià)指標(biāo)PMR 與AAMR。數(shù)據(jù)模擬程序和MDD判別通過自編R 語言程序?qū)崿F(xiàn),seq-GDINA 模型判別由自編R 語言程序調(diào)用G-DINA 包實(shí)現(xiàn)。
(4)實(shí)驗(yàn)結(jié)果
表3 列出了不同條件下的PMR 與AAMR 統(tǒng)計(jì)結(jié)果。可以看出,在不同實(shí)驗(yàn)條件下,滑動(dòng)概率越小,PMR 與AAMR 越好;非參數(shù)方法比參數(shù)方法更穩(wěn)定。
具體各判準(zhǔn)率之間的對(duì)比可查看圖1、圖2。圖1為各水平情況下的PMR,圖中可以清晰反映出在不同的滑動(dòng)概率情況下,兩種方法受滑動(dòng)概率影響均較大。在相同滑動(dòng)概率情況下,人數(shù)對(duì)MDD 基本沒有影響,但對(duì)seq-GDINA 影響較大,人數(shù)越多seq-GDINA 模型的判準(zhǔn)率越高。 本文設(shè)置人數(shù)最多為2000 人,但從圖中可以看出, 即使人數(shù)達(dá)到2000人,seq-GDINA 模式判準(zhǔn)率也與MDD 判準(zhǔn)率差異不大。且圖中還反映了,在低滑動(dòng)概率情況下,seq-GDINA 模式判準(zhǔn)率受人數(shù)的影響較小,高滑動(dòng)概率情況下,seq-GDINA 模式判準(zhǔn)率受人數(shù)的影響較大。 圖2 為各水平情況下的AAMR, 大致趨勢與PMR 一致,可以看到AAMR 指標(biāo)沒有PMR 敏感,與之前判斷一致。
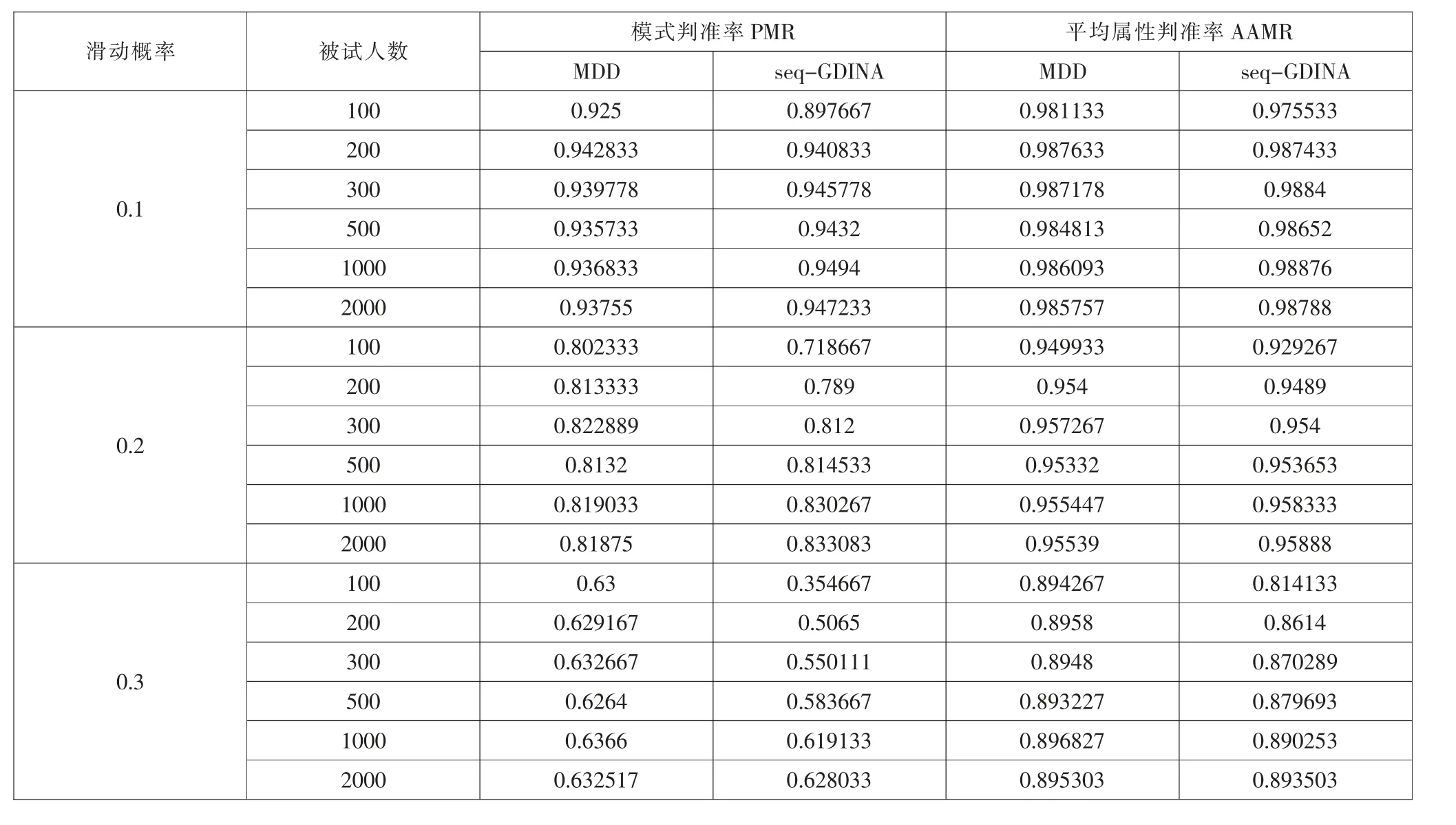
表3 PMR 與AAMR 指標(biāo)
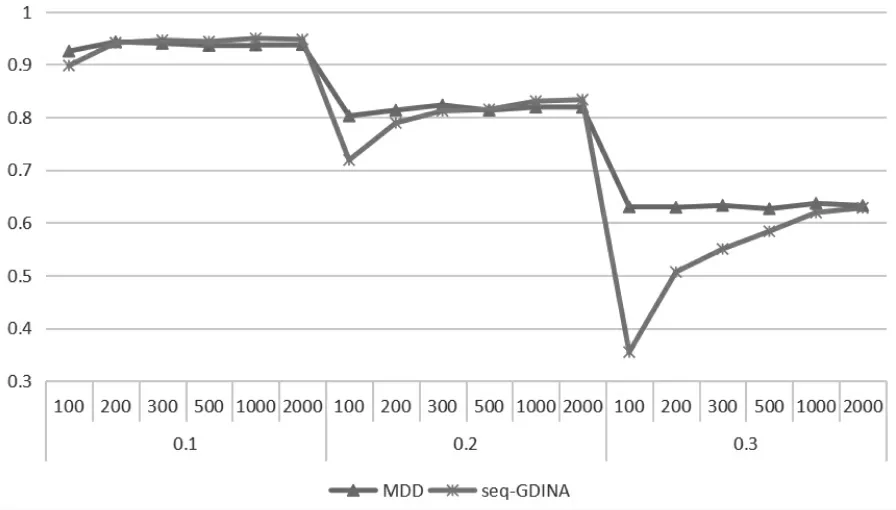
圖1 各水平下兩種方法判別結(jié)果PMR 值
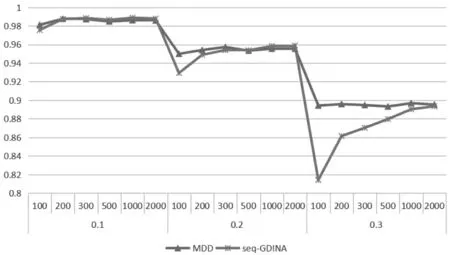
圖2 各水平下兩種方法判別結(jié)果AAMR 值
(5)小結(jié)
實(shí)驗(yàn)結(jié)果發(fā)現(xiàn),QC 矩陣評(píng)分方式在非參數(shù)方法上適用。 在項(xiàng)目質(zhì)量高時(shí),MDD 判別結(jié)果與seq-GDINA 模型在200 人以上時(shí)判別結(jié)果相當(dāng)。在項(xiàng)目質(zhì)量中等時(shí),MDD 判別結(jié)果與seq-GDINA 模型在500 人以上時(shí)判別結(jié)果相當(dāng)。在項(xiàng)目質(zhì)量低時(shí),MDD判別結(jié)果與seq-GDINA 模型方法在2000 人以上時(shí)判別結(jié)果相當(dāng)。以上結(jié)果說明,MDD 方法在QC 矩陣中完全適用,且在不同項(xiàng)目質(zhì)量情況下均有較好的判準(zhǔn)率。并且在方法選用上,建議在人數(shù)少于1000人時(shí),使用非參數(shù)MDD 方法更為合適,人數(shù)超過1000 人時(shí),可選用參數(shù)方法。
四、研究二:兩種評(píng)分方式在QC 矩陣中的比較
1.研究目的
不同評(píng)分方式對(duì)被試的判別有著直接影響。本部分使用非參數(shù)方法MDD 比較順序評(píng)分與非順序評(píng)分在不同項(xiàng)目質(zhì)量、被試人數(shù)下的判準(zhǔn)率情況,以驗(yàn)證非順序評(píng)分方法的有效性。
2.實(shí)驗(yàn)設(shè)計(jì)
實(shí)驗(yàn)采用2×3×6 四因素混合實(shí)驗(yàn)設(shè)計(jì),自變量分別為:評(píng)分方式、項(xiàng)目質(zhì)量和被試人數(shù)。每個(gè)實(shí)驗(yàn)條件重復(fù)進(jìn)行30 次。采用PMR 和AAMR 作為評(píng)價(jià)指標(biāo)。
3.實(shí)驗(yàn)流程
第一步:確定QC 矩陣,本研究采用與研究一相同的QC 矩陣(詳見附錄1)。判別方法為MDD。項(xiàng)目質(zhì)量為利用滑動(dòng)模擬方法模擬高質(zhì)量 (滑動(dòng)概率=0.1)、中等質(zhì)量(滑動(dòng)概率=0.2)、低質(zhì)量(滑動(dòng)概率=0.3)三個(gè)水平。評(píng)分方式為順序評(píng)分與非順序評(píng)分。被 試 人 數(shù) 為100、200、300、500、1000、2000 六 個(gè) 水平。屬性層級(jí)結(jié)構(gòu)為獨(dú)立型。
第二步:根據(jù)屬性個(gè)數(shù)與屬性層級(jí)結(jié)構(gòu)確定所有被試可能的KS,再根據(jù)順序評(píng)分與非順序評(píng)分確定測驗(yàn)QC 矩陣,兩者矩陣相乘并按步驟計(jì)分得到IRP,并在此基礎(chǔ)上模擬作答反應(yīng)數(shù)據(jù)。作答反應(yīng)數(shù)據(jù)生成的具體步驟與研究一相同。
第三步:分別使用順序評(píng)分與非順序評(píng)分方式,利用MDD 對(duì)模擬被試的ORP 進(jìn)行判別,并與真值進(jìn)行比較,得到兩個(gè)評(píng)價(jià)指標(biāo)PMR 與AAMR。數(shù)據(jù)模擬程序和MDD 均使用自編R 語言程序?qū)崿F(xiàn)。
4.實(shí)驗(yàn)結(jié)果
表4 列出了不同條件下兩種評(píng)分方式在兩種判別方法下的PMR 與AAMR 統(tǒng)計(jì)結(jié)果。可以看出,非順序評(píng)分方式判準(zhǔn)率高于順序評(píng)分方式。
具體兩種評(píng)分方式判準(zhǔn)率之間的對(duì)比可查看圖3、圖4。圖3 為兩種評(píng)分方式在各水平情況下的PMR,從圖中可以看出,在不同的項(xiàng)目質(zhì)量情況下,兩種評(píng)分方式的PMR 均有一個(gè)轉(zhuǎn)折點(diǎn), 但可以確定非順序評(píng)分判準(zhǔn)率優(yōu)于順序評(píng)分,且基本不受人數(shù)影響。圖4 為各水平情況下的AAMR,大致趨勢與PMR 一致。
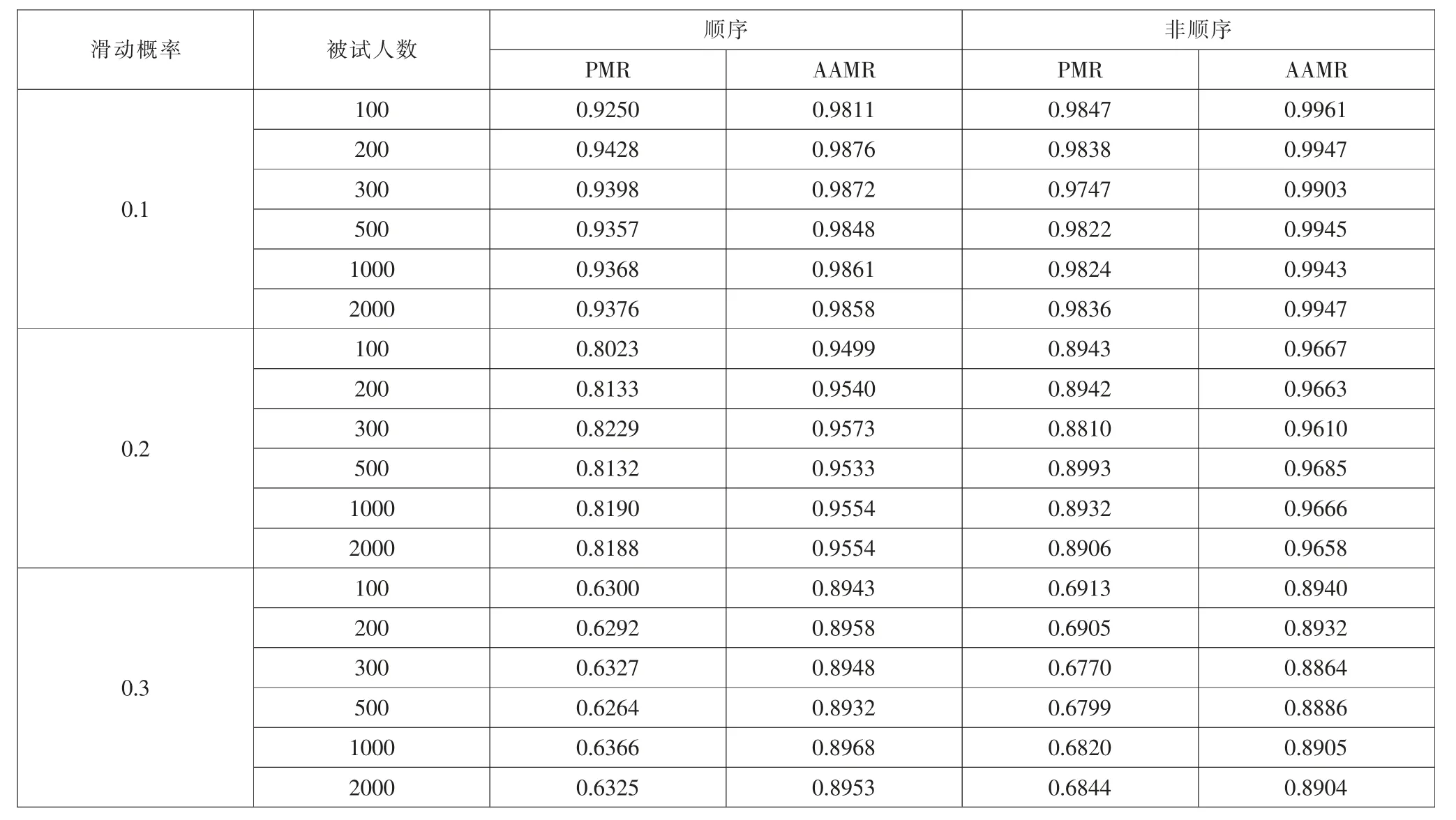
表4 PMR、AAMR 指標(biāo)
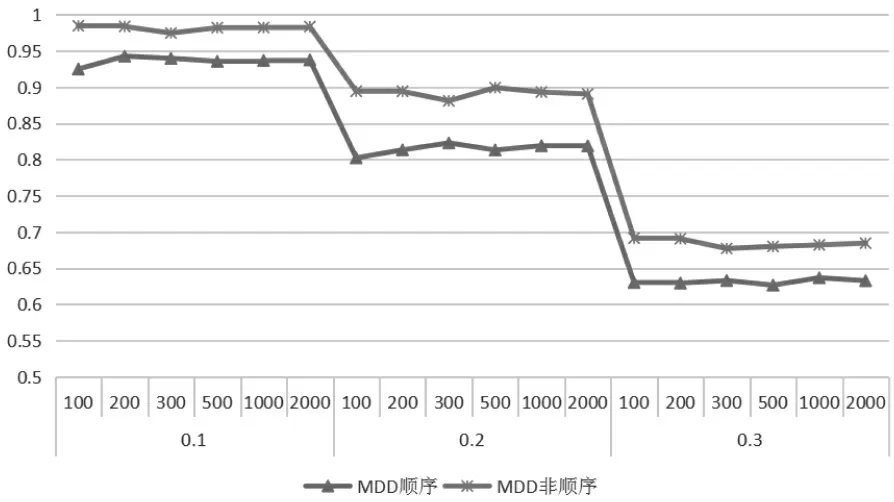
圖3 各水平下兩種評(píng)分方式判別結(jié)果PMR 值
5.小結(jié)
上述實(shí)驗(yàn)結(jié)果證明,在不同項(xiàng)目質(zhì)量、不同人數(shù)情況下,非順序評(píng)分均優(yōu)于順序評(píng)分;同時(shí)再次證明非參數(shù)方法基本不受人數(shù)影響,項(xiàng)目質(zhì)量越好,判準(zhǔn)率越高。
綜上所述,在實(shí)際運(yùn)用QC 測驗(yàn)時(shí),非參數(shù)方法十分有效,并且無論被試數(shù)量與項(xiàng)目質(zhì)量,非順序評(píng)分方式都可以優(yōu)先被考慮。
五、結(jié)論
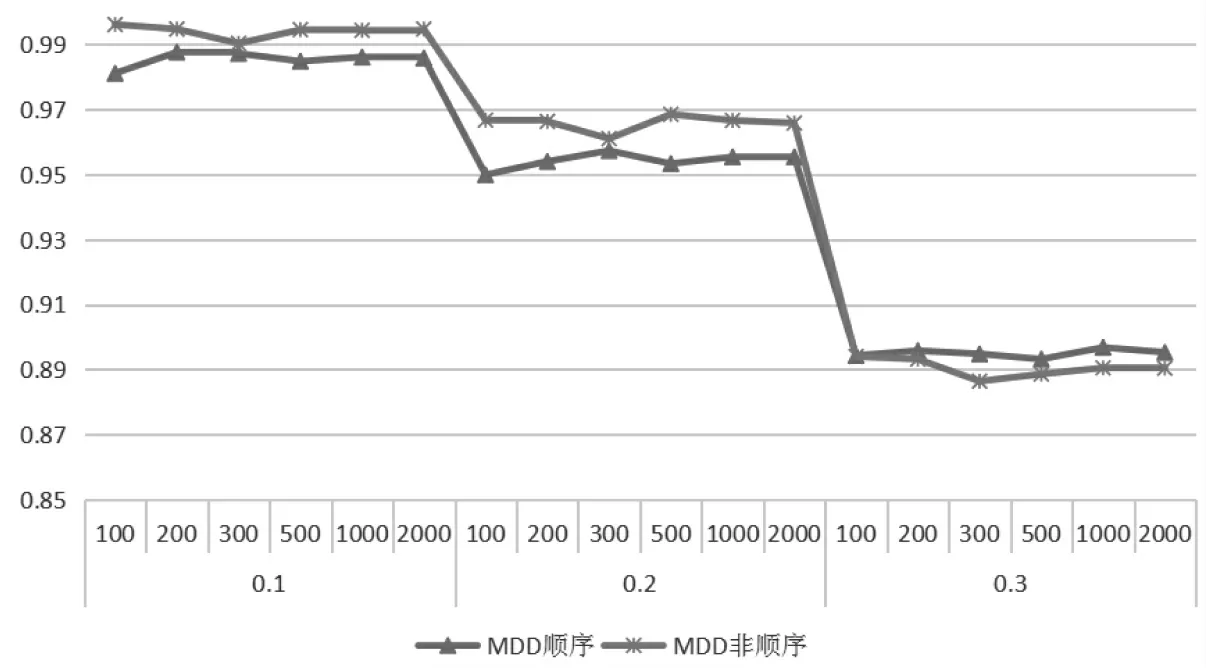
圖4 各水平下兩種評(píng)分方式判別結(jié)果AAMR 值
本研究探究了非參數(shù)方法(MDD)在QC 矩陣中的適用性,并且在原有QC 矩陣評(píng)分方式之上提出了一種新的評(píng)分方式。實(shí)驗(yàn)結(jié)果表明:第一,非參數(shù)方法在QC 矩陣中的判準(zhǔn)率較高,且當(dāng)樣本量較小時(shí)非參數(shù)方法判準(zhǔn)率比參數(shù)方法高,證明QC 矩陣評(píng)分方式在非參數(shù)方法中完全適用, 且非參數(shù)方法比參數(shù)方法更適于小樣本; 第二, 在不同條件下, 非順序評(píng)分方式均比順序評(píng)分方式擁有更高的判準(zhǔn)率。
研究對(duì)QC 矩陣的評(píng)分方式進(jìn)行探討,給應(yīng)用者提供理論支持,但依然存在一定不足。第一,對(duì)于QC 矩陣中可能存在的多策略問題的評(píng)分方式還未加以研究;第二,在實(shí)際應(yīng)用中,非順序評(píng)分方式需要評(píng)分者在評(píng)分時(shí)進(jìn)行分步給分,而不是只看最終答案評(píng)分,一定程度上會(huì)增加評(píng)分者工作量,但若是可以實(shí)現(xiàn)自動(dòng)評(píng)分技術(shù),該方法可以更準(zhǔn)確地判斷學(xué)生的知識(shí)狀態(tài)。
附錄1:QC 矩陣
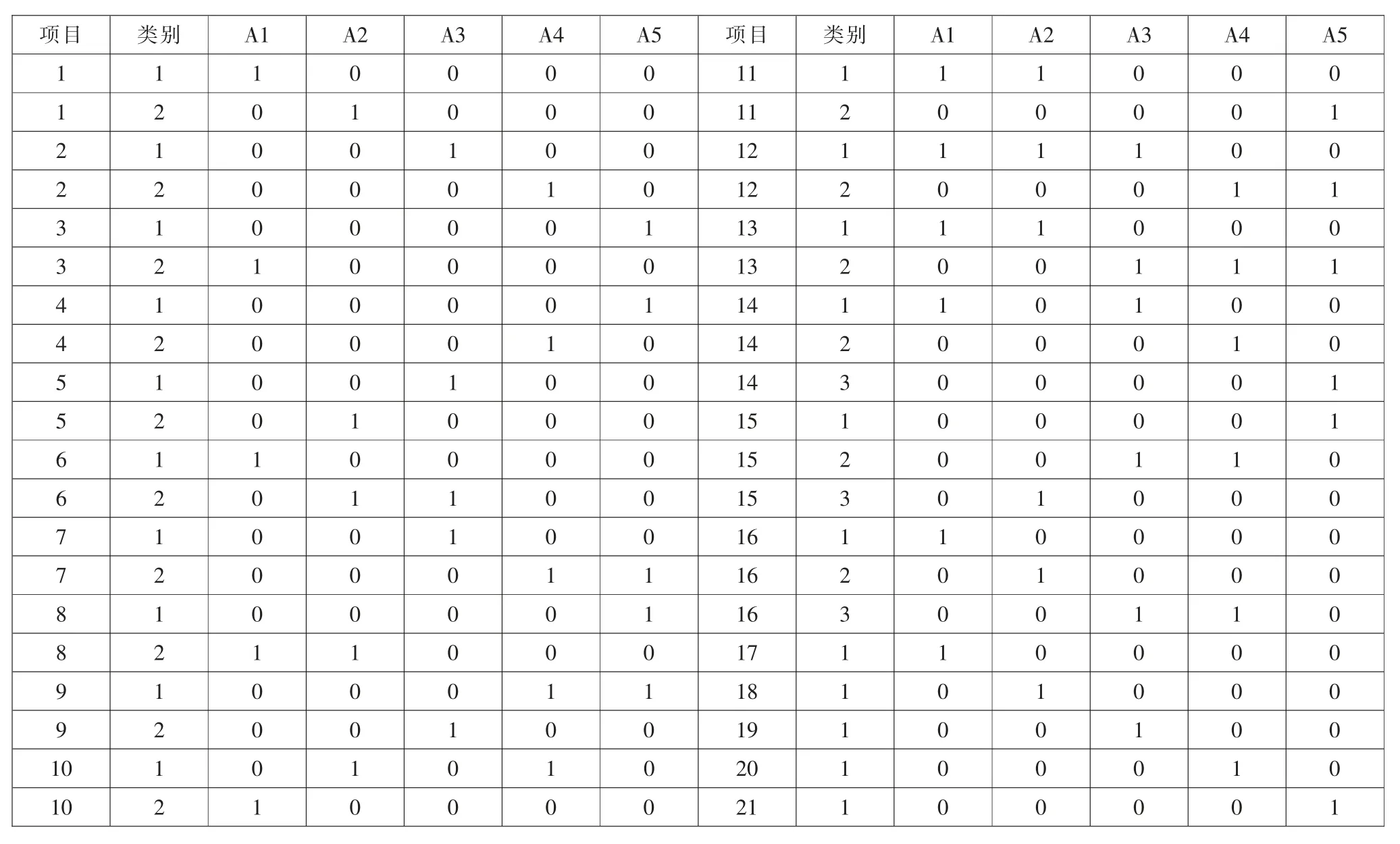
項(xiàng)目 類別 A1 A2 A3 A4 A5 項(xiàng)目 類別 A1 A2 A3 A4 A5 1 1 1 0 0 0 0 11 1 1 1 0 0 0 1 2 0 1 0 0 0 11 2 0 0 0 0 1 2 1 0 0 1 0 0 12 1 1 1 1 0 0 2 2 0 0 0 1 0 12 2 0 0 0 1 1 3 1 0 0 0 0 1 13 1 1 1 0 0 0 3 2 1 0 0 0 0 13 2 0 0 1 1 1 4 1 0 0 0 0 1 14 1 1 0 1 0 0 4 2 0 0 0 1 0 14 2 0 0 0 1 0 5 1 0 0 1 0 0 14 3 0 0 0 0 1 5 2 0 1 0 0 0 15 1 0 0 0 0 1 6 1 1 0 0 0 0 15 2 0 0 1 1 0 6 2 0 1 1 0 0 15 3 0 1 0 0 0 7 1 0 0 1 0 0 16 1 1 0 0 0 0 7 2 0 0 0 1 1 16 2 0 1 0 0 0 8 1 0 0 0 0 1 16 3 0 0 1 1 0 8 2 1 1 0 0 0 17 1 1 0 0 0 0 9 1 0 0 0 1 1 18 1 0 1 0 0 0 9 2 0 0 1 0 0 19 1 0 0 1 0 0 10 1 0 1 0 1 0 20 1 0 0 0 1 0 10 2 1 0 0 0 0 21 1 0 0 0 0 1
附錄2:順序的QC 矩陣
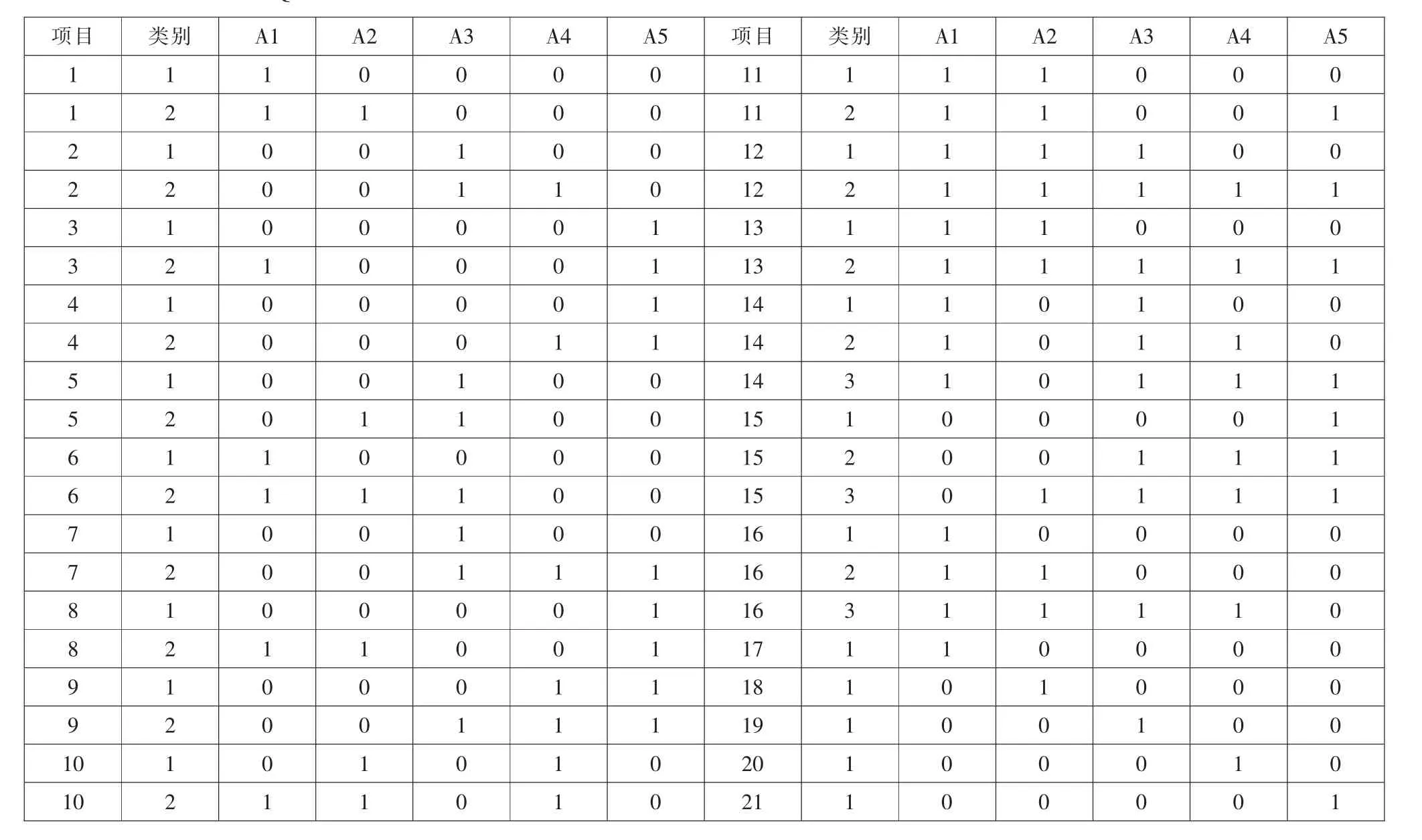
項(xiàng)目 類別 A1 A2 A3 A4 A5 項(xiàng)目 類別 A1 A2 A3 A4 A5 1 1 1 0 0 0 0 11 1 1 1 0 0 0 1 2 1 1 0 0 0 11 2 1 1 0 0 1 2 1 0 0 1 0 0 12 1 1 1 1 0 0 2 2 0 0 1 1 0 12 2 1 1 1 1 1 3 1 0 0 0 0 1 13 1 1 1 0 0 0 3 2 1 0 0 0 1 13 2 1 1 1 1 1 4 1 0 0 0 0 1 14 1 1 0 1 0 0 4 2 0 0 0 1 1 14 2 1 0 1 1 0 5 1 0 0 1 0 0 14 3 1 0 1 1 1 5 2 0 1 1 0 0 15 1 0 0 0 0 1 6 1 1 0 0 0 0 15 2 0 0 1 1 1 6 2 1 1 1 0 0 15 3 0 1 1 1 1 7 1 0 0 1 0 0 16 1 1 0 0 0 0 7 2 0 0 1 1 1 16 2 1 1 0 0 0 8 1 0 0 0 0 1 16 3 1 1 1 1 0 8 2 1 1 0 0 1 17 1 1 0 0 0 0 9 1 0 0 0 1 1 18 1 0 1 0 0 0 9 2 0 0 1 1 1 19 1 0 0 1 0 0 10 1 0 1 0 1 0 20 1 0 0 0 1 0 10 2 1 1 0 1 0 21 1 0 0 0 0 1
- 考試研究的其它文章
- TOECI 口語考試任務(wù)設(shè)計(jì)及其對(duì)漢語口語測試的啟示
- 計(jì)算機(jī)自適應(yīng)測驗(yàn)在美國護(hù)士執(zhí)照考試中的應(yīng)用
- 高校外語教師語言測評(píng)素養(yǎng)研究:以一次校本測試為例
- 皮亞杰認(rèn)知發(fā)展理論指導(dǎo)下的物理可測試核心素養(yǎng)水平及研究
- 中職語文三二分段教與學(xué)探究:基于2017-2019 年天津市“三二分段”中高職銜接統(tǒng)一考試語文學(xué)科數(shù)據(jù)的分析
- 布魯姆目標(biāo)分類視角下高考英語閱讀理解題思維能力層次分析:以2019 年高考試卷為例

