基于節點多屬性相似性聚類的社團劃分算法

邱少明,於 濤,杜秀麗,陳 波

(1.大連大學 通信與網絡重點實驗室,遼寧 大連 116622; 2.嶺南師范學院 信息工程學院,廣東 湛江 524048)

0 概述

網絡是由節點和連線構成,表示不同對象之間的相互聯系。在現實生活中,存在蛋白質網絡[1]、神經網絡[2]、社會網絡[3]等各種類型的網絡,不同的網絡具有不同的結構和屬性,而不同的屬性也會表現出不一樣的特征。隨著對網絡研究的進一步深入發現網絡中存在一種特殊的拓撲結構,其主要特點是在該網絡結構內的節點聯系非常緊密,在網絡結構之間的節點聯系相對稀疏,研究人員將該結構特征初步定義為網絡社團現象[4]。社會網絡的社團宏觀結構體現了網絡成員之間的聯系,反映了成員之間的關系屬性,可以被定義為社會成員之間緊密相連的集合。

目前,社團劃分方法主要包括基于模塊度的社團劃分方法、基于圖劃分的社團劃分方法和基于層次聚類的社團劃分方法。基于模塊度的社團劃分方法由NEWMAN于2004年提出[5],其核心是一種分層貪婪算法,如Fast-Unfolding算法[6],可以快速實現對社團的劃分,但容易陷入局部最優,不適用于大規模的網絡社團劃分?；趫D劃分的社團劃分方法[7]如Kernighan-Lin算法[8]、譜平分算法等,均是經典的圖譜理論劃分算法,需要預知社團數目才可實現社團劃分。基于層次聚類的社團劃分方法[9]盡管具有較好的社團劃分效果,但是聚類標準的選取對劃分質量影響較大。

在此基礎上,文獻[10]提出局部社團檢測算法,通過不同的隸屬函數進行動態檢測,但其是針對局部社團進行劃分,忽略了網絡全局特性,對網絡整體結構的判斷不夠準確,容易陷入局部最優。通過進一步研究發現,社團劃分與聚類問題非常相似,因此文獻[11]提出基于密度的聚類方法,相對于已有方法聚類效果有所改進,但其聚類的初始條件選取存在隨機性,會導致劃分的社團不穩定。文獻[12]提出相似性概念,但其在相似性網絡定義上很少從自身屬性進行考慮,并且社團劃分方法僅采用單一指標,如聚集系數[13],不具說服力。文獻[14]基于RA指標提出頂點相似性指標,并將其運用于推薦系統中,具有較好的推薦效果,但其僅針對小型網絡,如果將其運用于具有較多屬性的大型網絡中,則聚類效果會迅速下降。文獻[15]提出一種基于節點相異度的社團層次劃分算法,結合核度和接近度評估得出節點相異度評價結果,從而計算節點間的相似度。雖然該算法能夠針對性地選取初始節點,但相異度評估方式沒有考慮到網絡節點間的多屬性關系,僅通過節點之間的最短距離衡量相異程度,缺乏一定的合理性。相似性指標主要分為局部相似性指標與全局相似性兩類,常見的局部相似性指標主要有Jaccard指標[16]等,全局相似性指標主要有SimRank指標[17]等。文獻[18]提出一種綜合考慮用戶行為與相似度的社區發現算法,將網絡中用戶間的多維關系抽象成相似度,并將相關因子作為模塊度的目標函數進行社團劃分,能夠基本達到劃分的目的,但是精確度較低。由于上述研究方法多數僅考慮了網絡局部特性,未考慮網絡全局特性,存在劃分方法單一、劃分精度不高等問題,因此本文提出基于節點多屬性相似性聚類的社團劃分算法SM-CD。

1 節點多屬性相似性度量

1.1 網絡抽象

所有網絡都可以被抽象成節點及其連邊構成的結構,本文提出一種考慮節點多屬性的度量方法,將網絡中某節點與其鄰居節點直接相連的網絡節點之間的屬性稱為節點自身屬性,將非直接相連的網絡節點之間的屬性稱為結構屬性,從節點自身屬性和結構屬性角度出發,根據相似性進行社團劃分操作。

1.2 節點相似度計算

1.2.1 節點屬性選擇

由于網絡中的節點不是完全孤立存在的,而是與其他節點存在聯系,在社會關系網絡中其集聚性表現尤為明顯,因此集聚性是重要的節點自身屬性指標。

屬性1(聚集系數C) 節點i的聚集系數計算如式(1)所示:

(1)

其中,φi表示節點i的鄰居節點集合,|E(φi)|表示節點i的鄰居節點之間的實際連邊數目。

在社會網絡中,每個成員地位不同,有的成員與其他成員聯系少,但是他可能是兩個社團的中間聯絡人,如果忽視其作用,則可能導致兩個社團中的聯系出現中斷或者難度加大。如果網絡中的兩個個體沒有直接相連,且兩者之間不存在間接相連,則兩者之間存在阻礙,節點效率是用來描述該節點對網絡中其他相關節點的影響程度,是重要的結構屬性指標。

屬性2(節點效率Eef) 設節點數量為n,則節點i的效率計算如式(2)所示:

(2)

其中,j表示節點i的鄰接節點,l表示節點i和節點j的共同鄰接節點,Υil和Υjl分別表示節點l在節點i和節點j的鄰居節點中所占的比例。

屬性3(核度) 節點的核度定義為節點在核中的深度,核度的最大值對應網絡結構中最中心的位置。使用核度可以描述度分布所不能描述的網絡特征,揭示源于系統特殊結構的層次性。核值的大小可以將網絡中的節點按照影響力進行分類,在實際網絡中,核度越大的節點,影響力也相對較大。

屬性4(共有節點引力) 在進行網絡節點劃分時,節點歸屬的強弱是節點劃分的依據,如果兩個節點之間的共有節點集合越多,說明兩個節點之間的交互信息量越大,在考慮相似度時會在結構上產生更強的吸引力。因此,在定義共有節點引力時,共有節點占據相應節點的比例可以直觀反映兩節點在結構上的相似性。節點i和節點j的共有引力計算如式(3)所示:

(3)

其中,|φi,φj|表示節點i和節點j的共同鄰居數量,|φi|和|φj|分別表示節點i和節點j的鄰居節點數量,兩者的比值越大,說明兩類節點在結構上具有更強的關聯性。

1.2.2 節點屬性相似度矩陣求解

本文利用節點的多屬性信息結合局部與全局信息對網絡中的社團進行劃分,具體的相似性指標定義為:

(4)

在獲取中間矩陣后,需要進一步獲取不同節點之間的相似度矩陣,相似度矩陣描述了網絡中的各節點在各屬性協同下,依據不同的權重值計算出的相似情況,從而求解相似度矩陣SSim的每個值。例如,給定兩個節點vi和vj,其對應的屬性向量為hi和hj,則兩個矢量節點之間的相似度Sij計算如式(5)所示:

(5)

當i、j直接相連時,滿足式(6):

(6)

當i、j不直接相連時,滿足式(7):

(7)

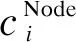
(8)

2 基于節點多屬性相似性聚類的社團劃分

2.1 節點多屬性相似性聚類

圖1描述了考慮節點不同屬性的社團劃分結果。在圖1(a)和圖1(c)中的簇節點劃分情況在不斷變化,因此在簡化社團結構圖1(b)和圖1(d)中反映的結果也存在差異。在圖1(a)中,當不考慮簇7節點的結構屬性(如共有節點引力及效率)而僅考慮節點的自身屬性時,整個網絡被劃分成3個社團如圖1(b)中簡化圖所示,當考慮網絡自身屬性時,網絡會分成4個社團如圖1(d)中簡化圖所示。

圖1 考慮節點不同屬性的社團劃分結果

根據節點多屬性定義可以利用本文聚類算法將不同節點劃分到不同社團結構中,因此,在進行社團聚類算法實現時,最重要的是如何使用聚類思想合理融合節點屬性信息并對社團進行劃分。在進行社團劃分時,本文考慮到節點的不同屬性,并在此基礎上,結合節點相似度矩陣SSim,提出一種基于節點多屬性相似性聚類的社團劃分算法。

傳統聚類算法是對于給定的基本樣本集,按照樣本之間的距離,將樣本集劃分為K個簇,使簇內的點盡量緊密連接在一起,而簇間距離盡可能大。在本文算法中,將各節點之間的相似度作為樣本集,即相似度矩陣中的各sij值,根據影響度函數選取初始質心節點,并采用聚類思想進行劃分操作。

1)社團K值的確定。依據當前研究發現,對于社團結構不是很明顯的網絡,無法在初期直接確定網絡中的社團數目。所以,本文在理論范圍內采用遍歷方式尋找最佳K值,選出最優劃分結構對應的K值即為最終輸出的社團數目。

2)聚類質心的選取。一個好的初始質點是均值聚類的必要條件,在選取聚類的初始質心時,本文從影響度的角度出發,而不是隨機選取初始點。由分析可知,如果某個頂點vi的周圍節點連接比較稠密,則表明該節點在網絡中具有較強的吸附能力,即更容易形成社團,則以這類節點作為質心節點相比于在網絡中隨機選取初始節點更具代表性。本文影響度函數的定義如式(9)所示:

(9)

其中,影響度函數f(vi)∈(0,1),用于衡量一個節點相對于其他節點的影響程度,d(vi,vj)表示節點vi和vj之間的歐幾里得距離,考慮到網絡節點之間的距離對影響度函數具有較大影響,所以本文引入?調節因子,通過?來調整不同距離之間的節點影響程度。在本文實驗中發現,如果不引入調節因子會導致計算出的指標值相近,區分效果不明顯。因此,本文依據影響度函數的大小,選取排名前η個的節點作為選取合理K值的依據。

2.2 算法描述

本文SM-CD算法的主要思想是同時考慮網絡節點的自身屬性與結構屬性信息得到中間矩陣,并利用節點相似度計算方法,將計算得到的相似度值作為聚類樣本集得到相似度矩陣,再結合影響度函數選取排名靠前的節點集合η作為遍歷上限值,通過不斷改變α與β,選取合理的K值,直至模塊度值達到最大,并將對應的K值作為最終社團劃分數量,算法具體流程如圖2所示。

圖2 SM-CD算法流程

SM-CD算法實現步驟具體如下:

輸入簡化了屬性值的無向圖G=(V,E)

輸出通過算法得到的社團劃分數目K與社團結構

步驟1輸入網絡的鄰接矩陣A。

步驟2計算網絡節點結構屬性與自身屬性得到中間矩陣M,其中屬性4是網絡中節點i與其他n-1個節點之間的共有引力,作為結構屬性,得到網絡的相似度矩陣SSim。

步驟3通過影響度函數選取前η個備選節點作為社團個數的有效集合,計算模塊度Q值。

步驟4判斷每次計算的模塊度是否增加,如果當前計算得到的模塊度差值持續增加,則調整K值繼續計算當前α與β取值條件下模塊度的變化情況,如果模塊度值沒有持續增加,則調整α與β的取值,跳轉至步驟2重新計算相似度矩陣,從而得到不同權重下的模塊度值。

步驟5統計在不同權重下的模塊度值,選取最大模塊度對應的K值,即社團劃分的最佳數量。

3 實驗設置

3.1 評價指標

3.1.1 模塊度

由于在真實網絡中無法預先明確網絡中的社團結構,因此在衡量社團劃分準確性時,本文采用模塊度Q作為評價指標。在每次進行節點聚類時,都會計算此時的模塊度大小并觀察其值的變化,從而決定是否將該節點劃分到相應社團中。

模塊度Q是常用的比較社團劃分質量的評價指標,其中Q∈[0,1],社團劃分的質量越高,其模塊度的值越大,社團內的節點相似性越強,社團劃分效果越好,Q的具體定義如式(10)所示:

(10)

3.1.2 劃分準確率

模塊度評價指標是聚類的內部評價指標,是一種無監督度量指標,雖然對于單個聚類有較好的評價效果,但是對于聚類最終結果與實際結果之間存在一定的誤差。因此,需要引入一種有監督度量指標劃分準確率S,作為外部評價指標,其值一般為準確劃分后的社團個數占全部節點的比例,如式(11)所示:

S=NR/N

(11)

其中,NR表示準確劃分的社團數目,N表示總節點數。

3.2 真實網絡實驗

為驗證本文算法的準確性,選取2個真實網絡,分別為Zachary網絡和Football網絡(http://www-personal.umich.edu/～mejn/netdata/),如表1所示。對這2個真實網絡進行實驗研究并將本文算法與其他算法進行性能比較,以驗證本文算法的有效性。

表1 真實網絡拓撲結構

3.2.1 Zachary網絡實驗

Zachary網絡是美國某大學空手道俱樂部的關系網絡,該網絡包含34個節點及78條邊,其中節點表示俱樂部成員,邊表示成員之間存在的關系。節點1代表教練,節點34代表校長。由于教練和校長對于俱樂部收費問題存在分歧,因此導致該俱樂部分成以校長和教練為核心的小社團。本文算法對Zachary空手道俱樂部網絡進行劃分,在進行多次實驗后發現,當K=2時,社團模塊度Q=0.427,此時β=0.5,調節因子?=0.4,劃分效果最優,社團劃分結果如圖3所示。

圖3 本文算法對Zachary網絡的社團劃分結果

通過本文算法對Zachary網絡結構進行社團劃分,將網絡劃分成2個社團,社團1主要以節點1為中心,社團2主要以節點34為中心。在設定初始值時,將網絡劃分出的社團個數對應網絡中的社團模塊度,基于本文算法得到Zachary網絡社團劃分模塊度與社團個數之間的關系如圖4所示。

圖4 Zachary網絡社團個數與模塊度的關系

3.2.2 Football網絡實驗

Football數據集是一個經典的社團研究數據集,該網絡由115個球隊的613場比賽抽象而成,如何根據不同球隊之間的實力合理劃分球隊,并合理安排相應的賽事是該實驗關注的重點。因此,采用本文算法對該網絡進行社團劃分,初步結果如圖5所示。將網絡劃分成10個社團,模塊度Q=0.619 6達到最大值,此時α=0.3、β=0.7、?=0.4,劃分效果最優。對網絡社團進行反復劃分實驗,最終得到的仿真結果如圖6所示,通過調節不同的α和β值,對不同社團個數計算網絡模塊度,可以看出當α=0.3、β=0.7時,模塊度Q=0.619 6達到最大值,可以認為當劃分得到10個社團時,網絡劃分結果最佳。

圖5 本文算法對Football網絡的社團劃分結果

圖6 Football網絡社團個數與模塊度的關系

3.3 結果分析

針對相同網絡數據集,將本文SM-CD算法社團劃分結果與經典的Newman算法、GN算法、NC算法[15]、基于節點特征向量的復雜網絡社團發現算法[16]、IJ-CD算法[19]、基于節點內聚系數的局部社團發現算法[20]和GD算法[21]劃分結果進行對比驗證,結果如表2、表3所示。

表2 針對Zachary網絡的算法劃分結果對比

表3 針對Football網絡的算法劃分結果對比

Newman算法基于貪心算法原則,選取模塊度增長最大或者減小最少的社區,將其合并為一個新社區,不斷迭代循環,將模塊度最大值對應的網絡社團作為最優社團劃分結果。該算法在降低時間復雜度的同時,準確度也相應降低。從表2、表3結果可以看出,本文算法相比Newman算法在模塊度上分別提升了15%和13%。

GN算法的主要思想來源于聚類分裂法,原理是使用網絡中的邊介數作為相似度的度量。首先計算網絡中所有邊的介數,找到介數最高的邊并將其從網絡中移除,重新計算網絡中剩余邊的介數,不斷重復該過程,直至網絡中的任一頂點作為一個社區為止。雖然該算法準確度相對較高,但時間復雜度也較高。對比表2的Zachary網絡與表3的Football網絡時間復雜度指標,傳統GN算法時間復雜度是O(n3),本文算法的時間復雜度比GN算法低一個數量級。

文獻[16]算法采用效能傳遞思想對社團進行聚類,與本文算法的區別是將網絡節點之間的距離倒數作為信息傳遞效能指標并構建矩陣,從而計算模塊度值作為劃分依據,算法考慮相對單一。IJ-CD算法通過改進Jaccard相似系數矩陣并選取部分特征值對應的特征向量作為聚類樣本,雖然時間復雜度和本文算法相當,但在劃分精度上本文算法相對更好。

文獻[20]算法與GD算法思想類似,通過選取最大度節點作為起始社團,不斷搜索其鄰居節點,將強社團結構定義作為節點添加的約束條件最大度節點,不斷添加至社團中形成新的社團,直至鄰居節點集為空時停止。與本文算法相比,雖然文獻[20]算法的時間復雜度比本文算法的時間復雜度低,但是其將網絡劃分為5個社團,使用本文算法將網絡劃分為2個社團,且模塊度與本文算法相比相差較多,本文算法在劃分精度方面優勢明顯。與此同時,文獻[20]算法在劃分精度上與其他算法相差很小。因此,本文算法劃分精度比文獻[20]算法高,更具實用價值。NC算法雖然對于Zachary網絡劃分的模塊度與本文算法很接近,但時間復雜度為O((m+n)m),其中m為邊數,在仿真網絡中m遠比n要大得多,因此其時間復雜度大于本文算法。在同等情況下,本文算法的劃分精度相比其他算法略高,劃分效果更好。

本文針對社團劃分采用相同網絡數據集,選取經典Newman算法、GN算法和IJ-CD算法與本文算法在時間消耗和準確率方面進行比較,如圖7和圖8所示。從圖7可以看出,與經典Newman算法、GN算法相比,本文算法時間消耗更少,優勢明顯,與文獻[20]算法的時間消耗相差較小,但從表2、表3以及圖8可以看出,本文算法在劃分準確率上更具優勢,劃分效果更好。

圖7 社團劃分算法的時間消耗比較

圖8 社團劃分算法的準確率比較

4 結束語

本文定義了網絡中的節點自身屬性和結構屬性,提出一種基于節點多屬性相似性聚類的社團劃分算法。根據兩類屬性在網絡上的權重不同,在實驗中通過不斷調整調節因子將網絡劃分為不同的社團結構并計算相應的模塊度。實驗結果表明,本文算法能有效提高社團劃分的準確率。但由于本文中考慮的網絡為無權無向網絡,而在實際生活中網絡節點之間的連接權重存在差異且可能具有方向性,因此下一步將對有權有向網絡社團劃分進行研究。