基于長短時(shí)記憶神經(jīng)網(wǎng)絡(luò)的硬件木馬檢測(cè)
胡 濤,佃松宜,蔣榮華
(四川大學(xué) 電氣工程學(xué)院,成都 610065)
0 概述
由于集成電路(Integrated Circuit,IC)的設(shè)計(jì)越來越復(fù)雜,且其設(shè)計(jì)和制造朝著全球化的方向發(fā)展,半導(dǎo)體公司已不能完全自行設(shè)計(jì)和制造出所有的集成電路,這導(dǎo)致部分集成電路的設(shè)計(jì)和制造將外包給世界各地的其他公司,而外包公司可能在半導(dǎo)體公司不知情的情況下惡意設(shè)計(jì)集成電路[1]。已有研究表明,集成電路不僅在制造外包過程中容易受到惡意操作,而且整個(gè)集成電路的開發(fā)鏈也容易受到惡意操作,這增加了集成電路中存在硬件木馬的可能性。硬件木馬是指一種惡意修改電路,常以旁路電路的形式添加在原本電路中,并在攻擊者的操控下達(dá)到破壞電路或者竊取數(shù)據(jù)的目的[2]。
硬件木馬的檢測(cè)方式多種多樣,目前國內(nèi)外的檢測(cè)方式主要包括邏輯檢測(cè)、延時(shí)特征檢測(cè)、失效性檢測(cè)、側(cè)道信息檢測(cè)等[3]。其中,側(cè)道信息檢測(cè)方法是通過檢測(cè)集成電路的側(cè)道信號(hào)來分析待識(shí)別芯片中是否存在硬件木馬,與其他檢測(cè)方法相比,側(cè)道信息檢測(cè)具有無損傷、低開銷、高性能等優(yōu)點(diǎn)。基于此,本文采用的檢測(cè)方法也屬于側(cè)道信息檢測(cè)方法。
文獻(xiàn)[4]通過支持向量機(jī)(Support Vector Machine,SVM)驗(yàn)證了包含觸發(fā)電路的硬件木馬檢測(cè)的可行性。文獻(xiàn)[5]提出一種基于自組織競爭神經(jīng)網(wǎng)絡(luò)的硬件木馬檢測(cè)方法,利用無監(jiān)督的學(xué)習(xí)算法對(duì)母本電路和待測(cè)電路進(jìn)行分類判別,自組織競爭神經(jīng)網(wǎng)絡(luò)可以有效分辨微弱信號(hào),而無監(jiān)督學(xué)習(xí)機(jī)制可以減少人為干預(yù),降低人為建立的數(shù)學(xué)模型不精確帶來的負(fù)面影響。文獻(xiàn)[6]提出一種基于激活路徑時(shí)延的硬件木馬檢測(cè)方法,擺脫對(duì)母本電路的依賴。文獻(xiàn)[7]通過主成分分析(Principal Component Analysis,PCA)結(jié)合歐式距離實(shí)現(xiàn)硬件木馬的檢測(cè),并發(fā)現(xiàn)PCA對(duì)硬件木馬檢測(cè)的識(shí)別率有一定的改善。文獻(xiàn)[8]通過基于粒子群算法和遺傳變異算法優(yōu)化的SVM指出,當(dāng)木馬面積較小時(shí)SVM無法準(zhǔn)確識(shí)別硬件木馬。文獻(xiàn)[9]通過梅爾頻率倒譜系數(shù)提取側(cè)道信息的梅爾頻譜,通過K均值算法初始化隱馬爾可夫模型的初始狀態(tài),實(shí)現(xiàn)了利用時(shí)序特征的硬件木馬檢測(cè),但是該方法對(duì)長時(shí)間序列的處理效果欠佳。
目前有關(guān)側(cè)道信息的研究多數(shù)是將整體側(cè)道信息作為分類器的輸入特征向量,未充分利用側(cè)道信息的時(shí)序特征。本文提出一種基于PCA和長短時(shí)記憶(Long Short-Term Memory,LSTM)神經(jīng)網(wǎng)絡(luò)的硬件木馬檢測(cè)方法,利用PCA壓縮時(shí)序特征,使用LSTM神經(jīng)網(wǎng)絡(luò)對(duì)側(cè)道電流信息的時(shí)序特征進(jìn)行學(xué)習(xí),以達(dá)到準(zhǔn)確判斷待測(cè)電路中是否植入了硬件木馬的目的。此外,本文還探究了在硬件木馬插入不同位置的情況下該方法的檢測(cè)效果。
1 本文檢測(cè)方法
本文檢測(cè)方法主要由PCA模塊和LSTM神經(jīng)網(wǎng)絡(luò)模塊兩部分構(gòu)成。通過PCA算法將高維樣本投影到其低維子空間中,解決樣本維度過高帶來的計(jì)算爆炸和數(shù)據(jù)冗余等問題,再把降維后的特征向量輸入給LSTM神經(jīng)網(wǎng)絡(luò)來進(jìn)行正常芯片和木馬芯片的分類。
1.1 PCA算法
PCA算法是一種常見的通過線性變換將高維特征向量映射到低維空間中的方法,其基于最大方差理論,使得降維后的特征向量盡可能保留最大方差。本文使用PCA算法的主要目的是用于降低計(jì)算量,防止計(jì)算爆炸,加快訓(xùn)練速度。同時(shí),PCA算法在其實(shí)現(xiàn)步驟上存在歸一化的步驟,可以在一定程度上抑制由工藝偏差帶來的噪聲。PCA算法的具體實(shí)現(xiàn)流程如下:
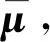
步驟2求解協(xié)方差矩陣R,計(jì)算方法如下:
(1)
步驟3求解協(xié)方差矩陣R的特征值λi和特征向量ui,計(jì)算方法如下:
λiui=Rui
(2)
其中,λi表示第i個(gè)特征值,ui表示其對(duì)應(yīng)的特征向量。直接求式(3)時(shí),要求協(xié)方差矩陣R必須為方陣,直接對(duì)R進(jìn)行求解容易引起維度爆炸,因此常常利用奇異值分解(Singular Value Decomposition,SVD)原理進(jìn)行處理。
步驟4取出SVD后按大小順序排列前k個(gè)特征值對(duì)應(yīng)的特征向量,并構(gòu)成變換矩陣Um×k=(u1,u2,…,uk)。其中,k由前k個(gè)方差貢獻(xiàn)率η決定,當(dāng)η大于設(shè)定的閾值時(shí),認(rèn)為前k個(gè)分量包含了原始特征向量的主要信息。方差貢獻(xiàn)率η的計(jì)算公式為:
(3)
步驟5對(duì)原始數(shù)據(jù)歸零化后再進(jìn)行線性變換,得到降維過后的特征向量X,計(jì)算公式為:
(4)
1.2 LSTM神經(jīng)網(wǎng)絡(luò)
LSTM神經(jīng)網(wǎng)絡(luò)是一種特殊的循環(huán)神經(jīng)網(wǎng)絡(luò)(Recurrent Neural Network,RNN),其具有時(shí)間遞歸的性質(zhì),適用于處理時(shí)序相關(guān)的問題,解決了RNN難以解決的時(shí)間序列長期依賴、梯度爆炸和梯度消失等問題。由于本文用來檢測(cè)硬件木馬的側(cè)道信息是時(shí)序相關(guān)的電流信息,因此可以使用LSTM神經(jīng)網(wǎng)絡(luò)來檢測(cè)硬件木馬。一個(gè)LSTM神經(jīng)網(wǎng)絡(luò)的內(nèi)部結(jié)構(gòu)如圖1所示。
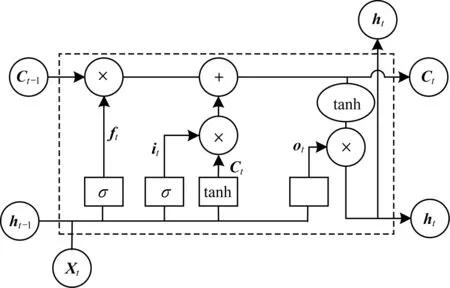
圖1 LSTM神經(jīng)網(wǎng)絡(luò)內(nèi)部結(jié)構(gòu)
在圖1中,t表示時(shí)間序列的順序,Xt表示輸入端,Ct表示當(dāng)前時(shí)刻的胞體狀態(tài),σ表示一個(gè)sigmoid函數(shù),其作用是將信息映射到0~1之間,表示是否允許信息通過,?表示逐點(diǎn)相乘,通常接在sigmoid函數(shù)后用來對(duì)信息進(jìn)行篩選,⊕表示向量相加,ht表示當(dāng)前時(shí)刻的輸出,tanh表示一層激活函數(shù)為tanh的神經(jīng)網(wǎng)絡(luò)層,W,b分別表示輸入信息到各個(gè)門的權(quán)向量和偏置向量。
LSTM神經(jīng)網(wǎng)絡(luò)的前向傳播過程按照式(5)的順序完成:
(5)
LSTM神經(jīng)網(wǎng)絡(luò)的訓(xùn)練一般通過跨時(shí)間的梯度反向傳播(Back Propagation Through Time,BPTT)算法對(duì)其各個(gè)參數(shù)進(jìn)行迭代更新[10]。
2 檢測(cè)流程
本文的檢測(cè)流程分為以下3個(gè)步驟:
步驟1對(duì)電路進(jìn)行仿真,提取側(cè)道電流信息。
步驟2通過PCA算法對(duì)數(shù)據(jù)降維,然后劃分訓(xùn)練集、測(cè)試集、驗(yàn)證集,其中測(cè)試集是由與訓(xùn)練集木馬插入位置相同的電路側(cè)道信息構(gòu)成,驗(yàn)證集是由與訓(xùn)練集插入位置不同的電路側(cè)道信息構(gòu)成。
步驟3訓(xùn)練分類器。
本文檢測(cè)方法的主要流程如圖2所示。
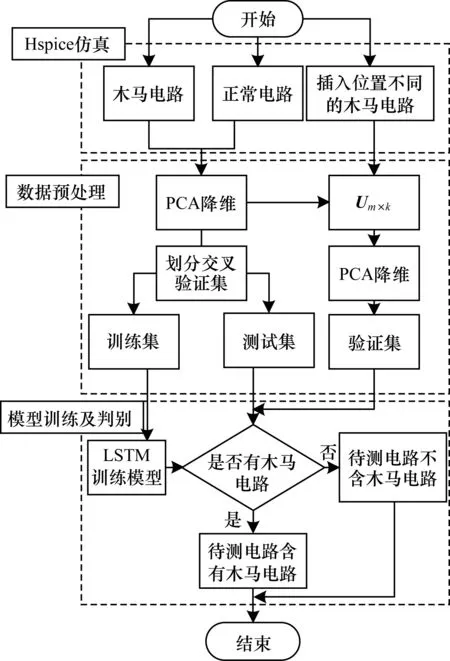
圖2 本文檢測(cè)方法的主要流程
其中,每一步的具體操作如下:
步驟1本文構(gòu)建的ISCAS89電路基于SMIC 0.18 μm工藝庫。通過Hspice仿真平臺(tái)得到多組電路的電流信息,第1組仿真實(shí)驗(yàn)以s9234電路作為母本電路,記作s9234。然后分別以1個(gè)、2個(gè)、3個(gè)s27電路作為木馬植入到s9234電路[11],分別記作s9234_1s27、s9234_2s27、s9234_3s27。利用Design Compiler綜合后得到的木馬電路分別占總電路面積的0.74%、1.33%、2.10%。這幾種木馬并沒有實(shí)際的攻擊功能,只是作為測(cè)試的旁路電路來驗(yàn)證本文方法的有效性。
為了進(jìn)一步驗(yàn)證木馬插入的位置對(duì)檢測(cè)有效性的影響。第2組仿真實(shí)驗(yàn)在第1組仿真實(shí)驗(yàn)的基礎(chǔ)上,分別以1個(gè)、2個(gè)、3個(gè)s27電路作為木馬植入到與第1組不同位置的s9234電路中,分別記作valid_s9234_1s27、valid_s9234_2s27、valid_s9234_3s27。
此外,本文利用Hspice基于蒙特卡羅方法模擬實(shí)際生產(chǎn)芯片時(shí)的工藝偏差(工藝偏差服從標(biāo)準(zhǔn)正態(tài)分布),得到160組側(cè)信道電流信息。
步驟2利用PCA算法對(duì)第1組仿真實(shí)驗(yàn)得到的數(shù)據(jù)降維,提取方差特征值貢獻(xiàn)率為前95%的特征向量矩陣Um×k,通過特征向量矩陣Um×k對(duì)第1組數(shù)據(jù)進(jìn)行變換得到降維后的特征向量X。接下來將特征向量X隨機(jī)劃分為訓(xùn)練集和測(cè)試集,本文選取33%的樣本作為測(cè)試集,記作test_s9234。
驗(yàn)證集由木馬插入位置不同的樣本構(gòu)成,通過特征向量矩陣Um×k對(duì)第2組數(shù)據(jù)進(jìn)行變換得到降維后的特征向量,記作valid_s9234。
步驟3利用訓(xùn)練集訓(xùn)練LSTM神經(jīng)網(wǎng)絡(luò)分類器,并在測(cè)試集上檢驗(yàn)本文分類器的準(zhǔn)確率,當(dāng)測(cè)試集的準(zhǔn)確率不再提升時(shí)即完成訓(xùn)練,然后在驗(yàn)證集上檢驗(yàn)分類器的準(zhǔn)確率。
本文的LSTM神經(jīng)網(wǎng)絡(luò)只包含一個(gè)LSTM層,且LSTM層內(nèi)的節(jié)點(diǎn)數(shù)為128個(gè)。在LSTM層后添加一層節(jié)點(diǎn)數(shù)為128、激活函數(shù)為Relu的全連接神經(jīng)網(wǎng)絡(luò)(Artificial Neural Network,ANN)層,對(duì)該全連接層的每個(gè)輸出節(jié)點(diǎn)以0.15的概率進(jìn)行Dropout,以增強(qiáng)網(wǎng)絡(luò)的泛化性[12],然后在Dropout層上添加激活函數(shù)為Softmax的全連接層作為整個(gè)網(wǎng)絡(luò)的最終輸出。此外,對(duì)整個(gè)網(wǎng)絡(luò)采用滑動(dòng)平均模型的方式來提高網(wǎng)絡(luò)的健壯性[13],使用學(xué)習(xí)率隨訓(xùn)練過程衰減的方式來增強(qiáng)網(wǎng)絡(luò)的學(xué)習(xí)能力[14],且基學(xué)習(xí)率為0.001,衰減率為0.99,網(wǎng)絡(luò)的訓(xùn)練算法為Adam算法。本文LSTM神經(jīng)網(wǎng)絡(luò)的運(yùn)算圖如圖3所示。
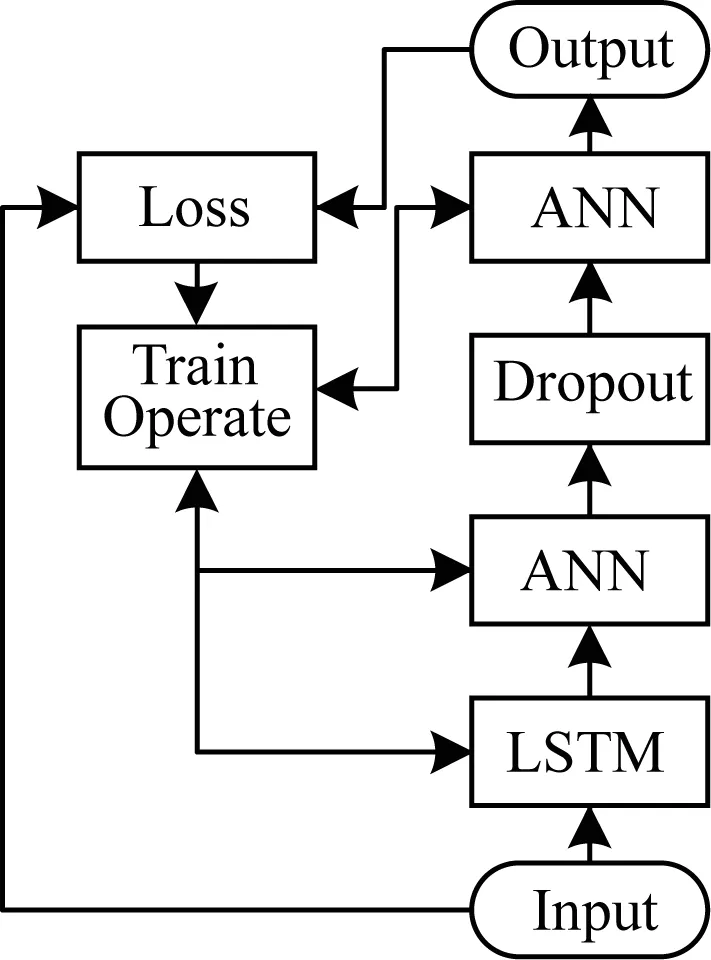
圖3 LSTM神經(jīng)網(wǎng)絡(luò)運(yùn)算圖
其中,箭頭表示數(shù)據(jù)的流動(dòng)方向,Input表示輸入PCA降維后的數(shù)據(jù)及其類別標(biāo)簽,LSTM表示一個(gè)LSTM神經(jīng)網(wǎng)絡(luò)層,ANN表示一層全連接神經(jīng)網(wǎng)絡(luò),Dropout表示Dropout層,Output表示預(yù)測(cè)結(jié)果,Loss表示交叉熵?fù)p失函數(shù),Train Operate表示用滑動(dòng)平均、學(xué)習(xí)率衰減、Adam算法對(duì)網(wǎng)絡(luò)進(jìn)行訓(xùn)練。
3 對(duì)比實(shí)驗(yàn)
為了驗(yàn)證本文方法的有效性,實(shí)驗(yàn)主要對(duì)SVM[15]、ANN[16]、隨機(jī)森林(Random Forest,RF)[17]、XGBoost等4種分類器結(jié)合PCA算法在相同的電路條件下進(jìn)行對(duì)比。
對(duì)比實(shí)驗(yàn)表明,SVM算法在小樣本、非線性樣本的判別中表現(xiàn)良好[18]。多次實(shí)驗(yàn)后,本文選取多項(xiàng)式核作為核函數(shù),懲罰參數(shù)C設(shè)置為10,核函數(shù)最高次冪degress設(shè)置為120,核函數(shù)系數(shù)gamma設(shè)置10,核函數(shù)的常數(shù)項(xiàng)為1。ANN具有極強(qiáng)的非線性映射能力,2個(gè)隱層的神經(jīng)網(wǎng)絡(luò)足以擬合任意非線性函數(shù)[19]。經(jīng)過多次試驗(yàn)后,本文的ANN包含2個(gè)隱藏層,每層128個(gè)節(jié)點(diǎn),使用Relu激活函數(shù),同樣采用滑動(dòng)平均和學(xué)習(xí)率衰減的方式來提高網(wǎng)絡(luò)的健壯性,且其基學(xué)習(xí)率為0.001,衰減率為0.99,網(wǎng)絡(luò)的訓(xùn)練算法為Adam算法。RF算法在處理高維數(shù)據(jù)時(shí)具有良好的泛化能力以及時(shí)間開銷低等優(yōu)點(diǎn),本文選擇RF算法的決策樹數(shù)目為50個(gè)[20]。XGBoost是一種極端的基于梯度提升機(jī)制的改進(jìn)算法,通過重復(fù)學(xué)習(xí)生成模型的殘差最終產(chǎn)生多個(gè)樹模型,從而組合成準(zhǔn)確率較高的綜合模型[21-22]。經(jīng)過多次試驗(yàn)后,本文選擇的XGBoost算法中每棵樹對(duì)訓(xùn)練樣本的隨機(jī)采樣率subsample為0.8,特征采樣率colsample_bytree為0.8,損失函數(shù)為均方差損失函數(shù)。
3.1 檢測(cè)結(jié)果
本文檢測(cè)方法在測(cè)試集test_s9234和驗(yàn)證集valid_s9234上對(duì)于每一個(gè)待測(cè)電路的分類結(jié)果如圖4所示。
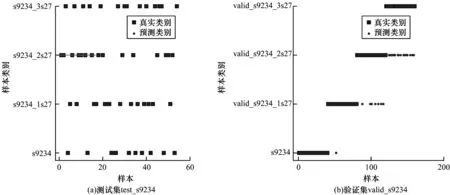
圖4 本文分類器在測(cè)試集和驗(yàn)證集上的分類結(jié)果
由圖4可知,在木馬插入位置相同的測(cè)試集上,檢測(cè)準(zhǔn)確率為100.00%,本文提出的分類器可有效識(shí)別木馬電路,因此不再單獨(dú)列出s9234_1s27、s9234_2s27、s9234_3s27的檢測(cè)準(zhǔn)確率。
在木馬插入位置不同的驗(yàn)證集上,檢測(cè)準(zhǔn)確率為83.13%,對(duì)正常電路s9234的召回率為100.00%,對(duì)面積比為0.74%的valid_s9234_1s27木馬電路召回率為97.44%,對(duì)面積比為1.33%的valid_s9234_2s27木馬電路召回率為82.05%,對(duì)面積比為2.10%的valid_s9234_3s27木馬電路召回率為53.85%。由此可見,隨著驗(yàn)證集木馬面積比的增大,檢測(cè)準(zhǔn)確率并沒有隨之增大,這是因?yàn)槟抉R插入位置不同導(dǎo)致其激活頻率不同,進(jìn)而導(dǎo)致每一種木馬電路的側(cè)道信息時(shí)序特征和訓(xùn)練集存在差異。在這種條件下,分類器只能判斷出電路是否植入了木馬電路,不能有效判斷具體插入了哪一種類型的木馬電路。若只考慮是否植入了木馬電路,則本文方法對(duì)正常電路的召回率為100.00%,對(duì)木馬電路的召回率為99.17%。
所有分類器在測(cè)試集、驗(yàn)證集的準(zhǔn)確率如表1所示。
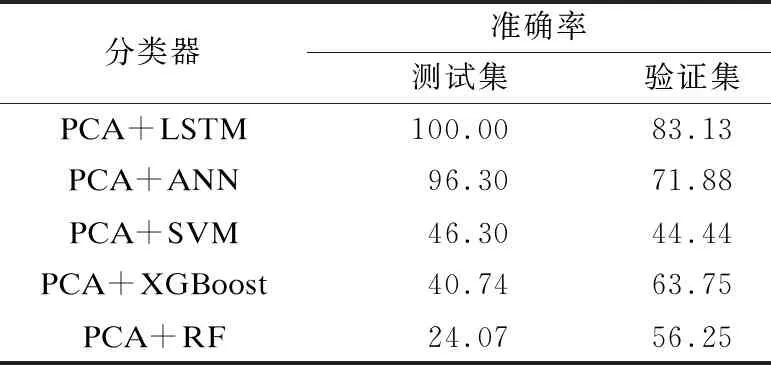
表1 不同分類器的檢測(cè)結(jié)果
3.2 分類器性能評(píng)價(jià)
本文提出的PCA+LSTM分類器在測(cè)試集test_s9234上的準(zhǔn)確率為100.00%,因此其混淆矩陣不在此列出。在驗(yàn)證集valid_s9234上的分類結(jié)果如表2所示。
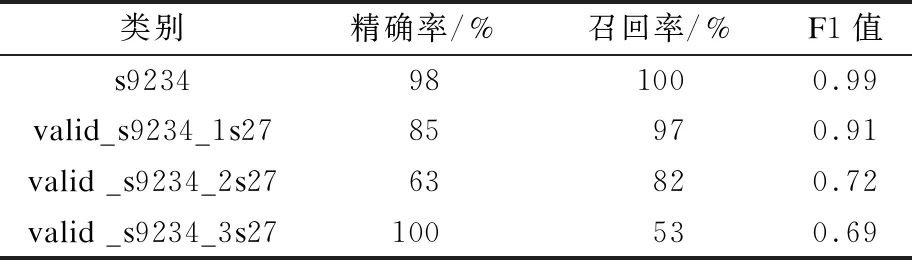
表2 本文分類器的分類結(jié)果
為了綜合評(píng)價(jià)分類器的分類性能,用每個(gè)分類器的每一個(gè)電路類別的F1評(píng)價(jià)指標(biāo)的加權(quán)平均值作為分類器的綜合評(píng)價(jià)指標(biāo)。每個(gè)分類器的加權(quán)F1綜合評(píng)價(jià)指標(biāo)如圖5所示。由表1和圖5可知,并不是所有的分類器都能有效識(shí)別硬件木馬,在用PCA方式作為提取特征向量的手段時(shí),傳統(tǒng)的機(jī)器學(xué)習(xí)分類器SVM、RF、XGBoost無法檢測(cè)出硬件木馬,分析原因在于這3類分類器的學(xué)習(xí)能力還不足以處理當(dāng)硬件木馬面積占比很小時(shí),由木馬產(chǎn)生的側(cè)道電流信息被生產(chǎn)工藝偏差帶來的電流偏差所覆蓋的問題。但是PCA+ANN分類器和本文提出的PCA+LSTM分類器都可以有效處理上述缺陷,分析原因在于ANN和LSTM具有比傳統(tǒng)的機(jī)器學(xué)習(xí)分類器更強(qiáng)的學(xué)習(xí)能力。
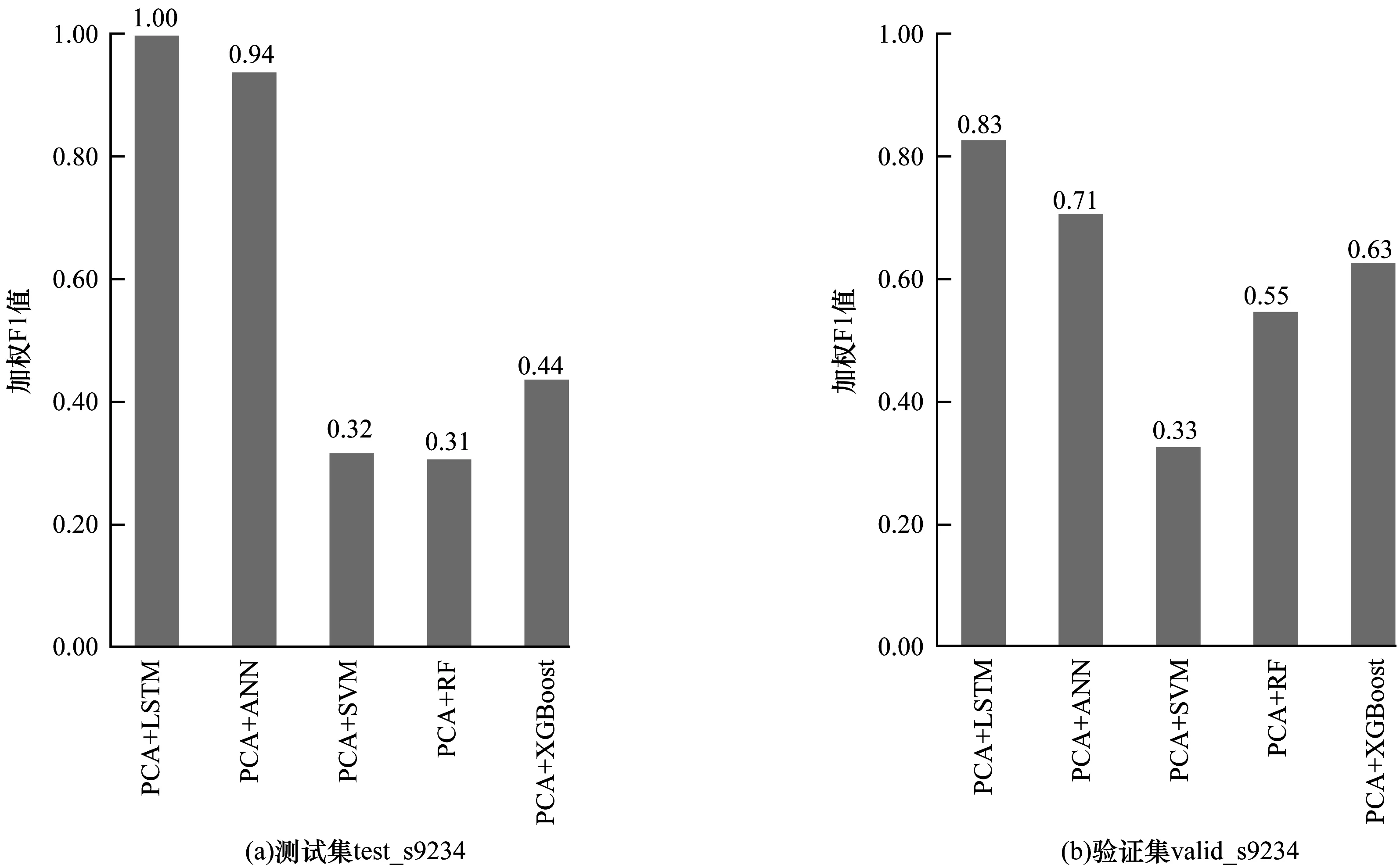
圖5 5種分類器在測(cè)試集和驗(yàn)證集上的加權(quán)F1評(píng)價(jià)指標(biāo)
本文主要對(duì)比PCA+LSTM和PCA+ANN分類器的性能。從圖5可以看出,在測(cè)試集test-s9234上,使用PCA+LSTM分類器的加權(quán)F1值為1.00,相較于PCA+ANN分類器提高了6.38%,在驗(yàn)證集valid-s9234上的加權(quán)F1值為0.83,相較于PCA+ANN分類器提高了16.90%。
4 結(jié)束語
本文提出一種將PCA和LSTM神經(jīng)網(wǎng)絡(luò)相結(jié)合的硬件木馬檢測(cè)方法,并通過實(shí)驗(yàn)驗(yàn)證了該方法的可行性。在測(cè)試集上的實(shí)驗(yàn)結(jié)果說明本文方法可以有效檢測(cè)出硬件木馬,但是在驗(yàn)證集上的實(shí)驗(yàn)結(jié)果也暴露出一些問題,如硬件木馬植入位置不同會(huì)導(dǎo)致硬件木馬的激活率發(fā)生改變,進(jìn)而使其時(shí)序特征發(fā)生改變,無法準(zhǔn)確判斷植入的木馬類型。因此在接下來的工作中,將會(huì)進(jìn)一步深入探究硬件木馬的激活率與時(shí)序特征的關(guān)系。

