平面流動皂膜的表面張力系數及厚度測量

周澤友, 萬冬梅, 徐海濤

(1.清華大學 燃燒能源中心, 北京 100084; 2.清華大學 能源與動力工程系, 北京 100084; 3.清華大學 航天航空學院, 北京 100084)

0 引 言

當液體中加入表面活性劑后，由于表面活性劑分子的存在，液體的表面張力降低，可以形成比一般液膜更穩定、更薄的皂膜。皂膜已經被廣泛應用于實驗研究，例如，Cohen等[1]研究了重力作用下超大皂膜泡的形狀，并據此提出了類似帳篷、氣膜館等膨脹結構的一種優化外形；Couder等[2]開創性地提出利用平面皂膜模擬二維流動；Chomaz等[3]系統分析了平面皂膜流動與二維流動的相似性。皂膜流動還被廣泛應用于研究二維繞流[4-6]、湍流流動[7-17]以及流固耦合等問題[18]；此外，由于皂膜中的擾動以表面張力控制的表面波形式傳播，傳播速度較小，容易產生流速大于波速的“超聲速”狀態，利用皂膜流動這一特點，可以研究激波傳播以及超聲速流動問題[19-22]。

國內學者也廣泛開展了皂膜流動實驗，針對二維流動[23-24]、流固耦合[25]、表面張力梯度導致的對流[26]、表面活性劑對皂膜流動的影響[27-28]以及皂膜與激波相互作用[29]等問題進行了研究。

雖然皂膜流動實驗已被大量開展，但在單一實驗中，極少會對皂膜流動參數進行全面評估。例如，在利用皂膜流動開展二維擾流或二維湍流研究時，其關注點往往僅限于流場，而對其他參數(如皂膜表面張力系數、皂膜厚度等)的影響，通常予以忽略。在利用皂膜進行激波或超聲速研究時，表面張力系數通常借用半無限深流體表面張力系數分析的結果，同時假設皂膜厚度均勻[20]，由此得到一個“聲速”，并認為其在皂膜內處處相等。但是，通過紅外吸收法測量得到的皂膜厚度顯示：即使對于穩定流動，皂膜厚度也并非處處一致，且厚度剖面還會隨總流量的變化而變化[30]。此外，對于皂膜這一類極薄液體層，表面張力系數也取決于皂膜厚度[2]。在此情形下，很難認為皂膜內的擾動波傳播速度是均勻的。

根據界面所處的狀態，表面張力系數測量方法主要分為兩類：靜態測量方法和動態測量方法。前者基于界面上的力平衡間接測量表面張力系數，包括平板法、掛環法、毛細管上升法、體積法和懸滴法等[31-32]；后者則是在界面動態變化時對其表面張力系數進行測量，包括最大氣泡壓力法、振動液滴法、振動射流法和氣泡射流法等[33]。這些方法都需要另外構造實驗裝置，并不是流動皂膜的直接測量方法。

本文基于皂膜邊界上的力平衡嚴格推導了豎直皂膜的邊界形狀方程，證明了新近文獻中的一個半經驗公式[34]，并提出了一種新的、更簡便易行的皂膜表面張力系數測量方法。對于流動皂膜的厚度，一般采用光學手段進行測量(比如利用皂膜對多個波長可見光的干涉[35-36]，或利用皂膜對特定波長紅外輻射的吸收)，并假定皂膜和水的吸收特性一致[30,37]。本文結合測得的速度剖面，發展了一種新的皂膜厚度的干涉測量法，在不需假定皂膜吸收特性的前提下以單個波長光源實現厚度測量。在自主搭建的重力驅動平面流動皂膜實驗裝置上，利用本文提出的方法測量了皂膜的表面張力系數、厚度和流動速度。

1 重力驅動平面流動皂膜實驗裝置

搭建的平面流動皂膜實驗裝置如圖1所示。參考文獻[12-13]，并經反復嘗試，本文采用質量比為2∶10∶88的Dawn牌商用洗碗液+甘油+去離子水混合配制皂液。洗碗液中含有表面活性劑十二烷基硫酸鈉，可以降低水的表面張力系數，使皂膜富有彈性，從而具有一定的抗干擾能力[27-28]；甘油可以增強混合液的黏性，減緩皂膜內部相對運動，使之更加穩定。

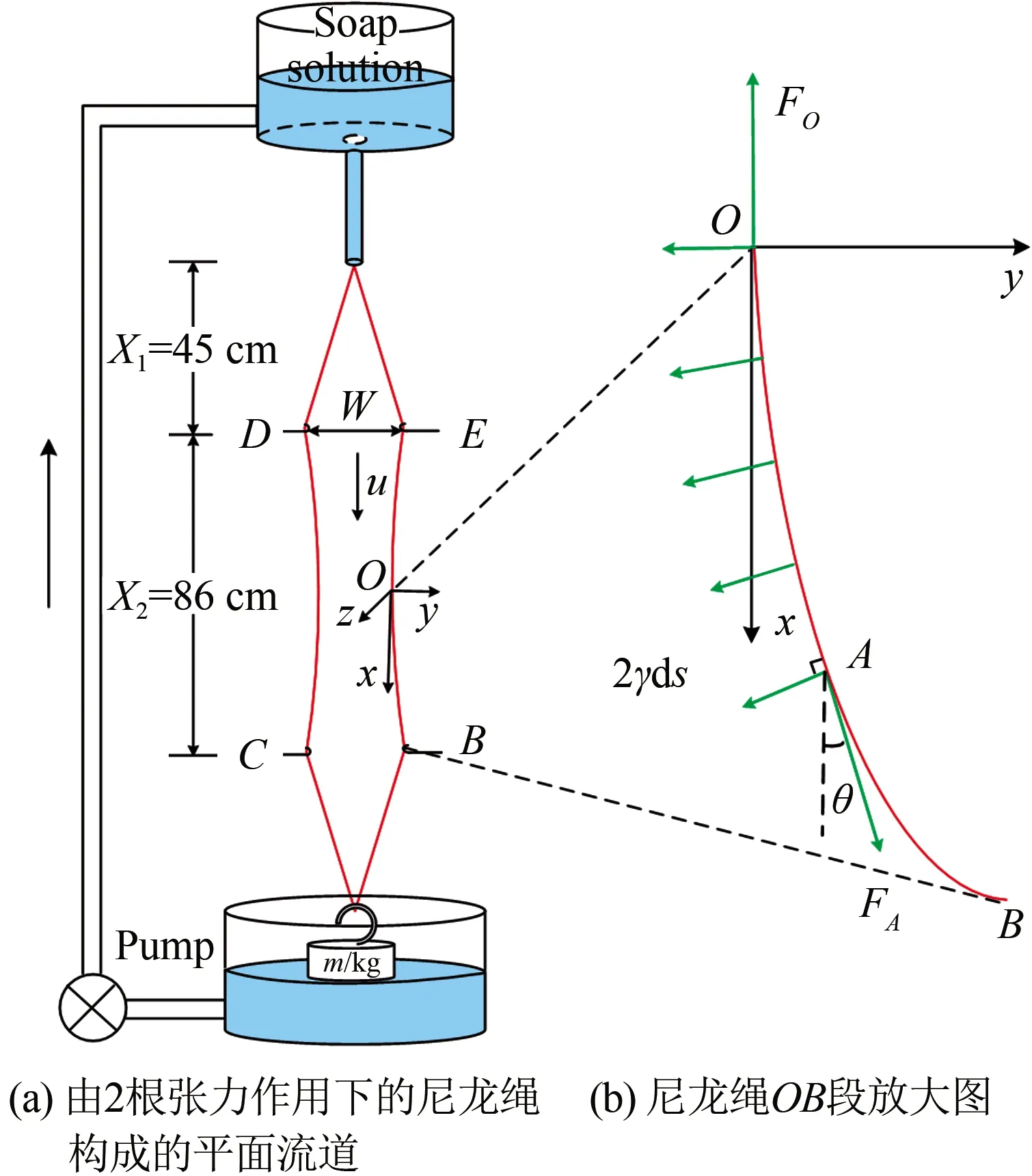
圖1 豎直平面流動皂膜實驗裝置圖

如圖1(a)所示，配制的皂液盛于上水箱中，經一個狹長的出水管流出，進入一個由兩根直徑為0.32 mm的尼龍繩構成的豎直平面流道(實驗中，尼龍繩一直處于下方砝碼施加的張力作用下)。緊接出水管口的流道為漸擴的擴張段，其下為流道寬度不變的實驗段和流道逐漸收窄的收縮段(在本文實驗中，擴張段長度X1=45 cm；實驗段長度X2=86 cm，實驗段入口寬度W=5 cm)。在擴張段，皂液在重力驅動下加速，當重力和空氣阻力平衡時充分發展，最終在實驗段達到勻速運動，之后經收縮段流入下水箱，再被泵回至上水箱，形成往復循環。

實驗啟動時，兩根尼龍繩貼合在一起；尼龍繩被皂液完全浸潤后，緩慢向兩側移動B、C、D和E點的掛鉤，分開尼龍繩至指定寬度，在兩繩之間形成穩定流動的皂膜。皂膜的平均速度和平均厚度可以通過調節泵的流量加以控制。當泵的流量Q=5～60 mL/min時，可以得到平均速度u=1～4 m/s、平均厚度h=3～9 μm的穩定豎直流動的平面皂膜。

下文對該平面流動皂膜進行力平衡分析，并由此推導出一種測量皂膜表面張力系數的方法；利用激光干涉法測量皂膜厚度，并簡要介紹皂膜速度的測量。

2 皂膜表面張力系數測量

由于皂膜厚度很小，其表面張力系數不能簡單采用對半無限深液體表面張力系數分析的結果[2]。Sane等[34]通過皂膜的力平衡分析得到一種測量皂膜表面張力系數的簡便方法，但在推導中多處采用了近似方法。本文給出一個嚴格推導，得出確切結論，并通過后文介紹的平面流動皂膜測量結果對該結論進行檢驗，證明推導的正確性；在此基礎上，計算皂膜的表面張力系數。

如圖1(a)所示，尼龍繩BE和CD下方懸掛質量為m的砝碼以施加張力、保持流道穩定。當沒有皂液流動時，尼龍線BE和CD在砝碼作用下保持鉛直；當皂液流入流道形成皂膜，尼龍繩BE和CD在皂膜表面張力的作用下向皂膜側略微收縮，形成微微內凹的流道(圖中對內凹程度有所放大)。從力平衡的角度出發，推導出該內凹曲線的形狀與皂膜表面張力系數的關系，可以給出一種測量流動皂膜表面張力系數的方法。

選取尼龍繩BE的中點O為坐標系原點，x軸為重力方向。設A為尼龍繩OB段上任一點，坐標為(xA,yA)，對尼龍繩段OA進行受力分析。簡單的受力大小估計表明：當皂膜流向方向的尺寸在1 m量級、砝碼自重在1 kg量級時，尼龍繩自重、流動皂膜對尼龍繩的動壓力、黏性力等都至多為尼龍繩張力的1/104，在后續分析中忽略它們對尼龍繩力平衡的影響。因此，尼龍繩受到點O、點A的拉力FO、FA以及尼龍繩上各微元段ds=dx/cosθ(x)的表面張力，其中，θ(x)表示尼龍繩上一點x處切向方向與重力方向的夾角。由于對稱性，在中點O處θ(0)=0。因此，尼龍繩段OA在水平和豎直方向的受力平衡關系式分別為：

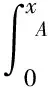
(1)

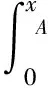
(2)

在推導式(1)和(2)時，假設皂膜邊界上的表面張力系數γ不隨位置而變化(對于充分發展達到穩定流動的皂膜，此假設是合理的)；式中的系數“2”是考慮到皂膜前后表面都會對尼龍繩產生表面張力。

將式(1)和(2)相除，并注意到點A的任意性，可以得到描述流道內凹形狀的曲線方程：

(3)

對式(3)積分，并結合邊界條件y(x=0)=0，得到曲線方程如下：

(4)

式(4)中包含未知參數FO(即尼龍繩中點O處的拉力)，其值可以通過將式(2)應用于B點，并代入B點處尼龍繩的力平衡關系FBcosθ(xB)=mg/2得到：

(5)

式中，L為BE段尼龍繩長度，推導式(5)時使用了xB=L/2。式(4)可稍加整理為：

(6)

其中，參數2γL/FO的值為：

(7)

式(6)和(7)即為邊界曲線形狀的準確方程。在推導方程的過程中，除物理上的簡單假設(如忽略尼龍繩自重)外，未作任何數學上的近似。

與懸掛物(砝碼)的重力相比，表面張力通常很小。例如，當L=1 m、m=1 kg時，取純水的表面張力系數γ=72 mN/m，得到2γL/(mg)≈1.5×10-2，代入式(7)得到2γL/FO≈3.0×10-2。記ε=2γL/FO，ε′=2γL/(mg)，則ε和ε′為同階遠小于1的小量。因此，對式(6)關于ε進行小參數展開可得：

(8)

式(8)表明：流道邊界曲線方程可以很好地用拋物線來近似(因為下一階修正項為ε3項)，并且給出了確切的系數，可以據此測出皂膜的表面張力系數。在實際應用中，可以利用ε′?1對其進一步簡化得到：

(9)

或

(10)

為驗證曲線方程(10)，在砝碼質量m=0.2 kg、皂液流量Q=35 mL/min時，實測了穩態流動皂膜狀態下尼龍繩的位置坐標，如圖2中的離散點所示。尼龍繩位置通過照相得到，為獲得較大范圍內的圖像，采用的放大倍數為1個像素對應0.35 mm的物理尺寸。對尼龍繩圖像在水平方向的光強分布進行高斯函數擬合以獲得亞像素的定位精度[38]。圖2中的光滑曲線是采用式(10)進行擬合的結果，與實測曲線吻合良好，驗證了分析的正確性。利用已知的砝碼質量，可以進一步得到表面張力系數γ=27.5 mN/m。值得注意的是：當砝碼質量很小時，表面張力引起的流道收縮很大(在中點O處達到最大值12%)，為避免由此帶來的流速和厚度場改變，在流動皂膜實驗中一般使用m=2 kg的砝碼。

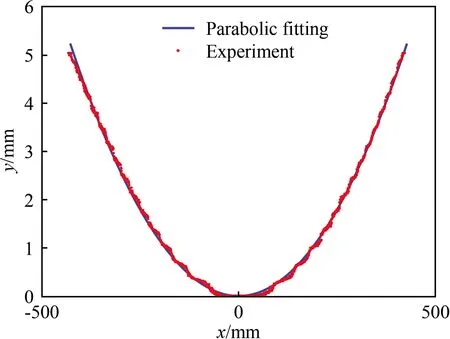
圖2 流道邊界實測值(紅色點)與理論分析(藍色線)對比

Sane等[34]推導了表面張力系數與尼龍繩曲線方程的關系，但并未獲得曲線方程的精確解，而是采用高階多項式對實測曲線進行擬合，發現選取二階多項式可以得到較好的結果，從而也獲得了式(10)，并通過擬合系數得到了表面張力系數。本文的嚴格推導說明：流道邊界曲線是拋物線加上高兩階小量的修正。圖(2)也證明了這一推導結論的正確性。

采用測量邊界曲線形狀的方式來獲得表面張力系數，在實驗上存在一處困難：通常邊界曲線曲率較小，為測出其具體形狀必須拍攝較大范圍；對于幅面大小一定的相機，這意味著空間分辨率的降低，給準確確定邊界曲線帶來了一定困難。因此，本文提出一種新的、更簡便易行的表面張力系數測量方法。

根據式(10)，可以給出流道中點O在有皂膜流動時相對于無皂膜流動時(即尼龍繩為豎直狀態時)的位移：

(11)

因此，通過測量給定砝碼質量下流道中點O的位移，就可以很方便地使用式(11)得到皂膜的表面張力系數。此方法的一個優點是：無需拍攝大范圍的尼龍繩圖像，照相時可以采用較大的放大倍數，獲得較高的空間分辨率。在實際應用時，本文采用了每像素對應0.01 mm物理尺寸的分辨率。根據式(11)，γ≈2mgyO/L2，砝碼質量m=(500±1)g和尼龍繩長度L=(500±1)mm的測量都可以控制在0.2%的測量偏差范圍內。當yO=(1±0.01)mm的測量偏差范圍降低至1%，實現了僅有2%左右不確定度的表面張力系數測量。

圖3給出了在同一皂液流量Q= 35 mL/min下測得的流道中點O的位移隨砝碼質量的變化以及根據式(11)擬合的直線。所有數據點都很好地落在過原點的擬合直線上，進一步驗證了本文推導的正確性。根據直線斜率測得的表面張力系數γ=27.1 mN/m，與前述拋物線擬合法得到的結果相近。

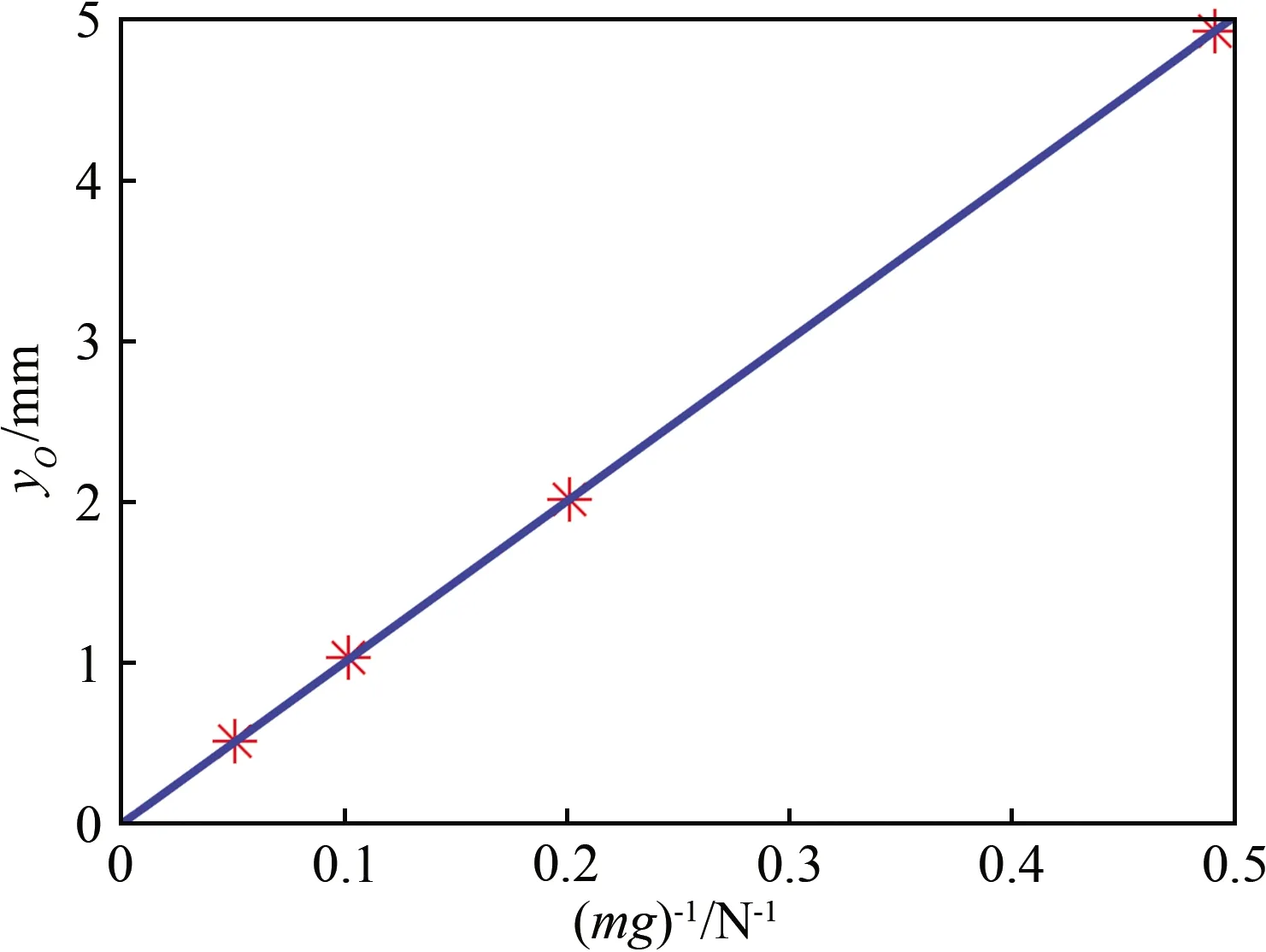
圖3 流道中點O在有/無皂膜流動時的位移量隨砝碼質量的變化

利用這一方法，還測量了表面張力系數隨皂液流量的變化關系，如圖4所示。圖中曲線并非如部分文獻報道的“表面張力系數隨皂液流量增加而單調下降”[34]，這可能是由于表面張力系數隨皂膜厚度變化而有所變化[2]、且實驗中皂膜厚度并非均勻分布導致的。

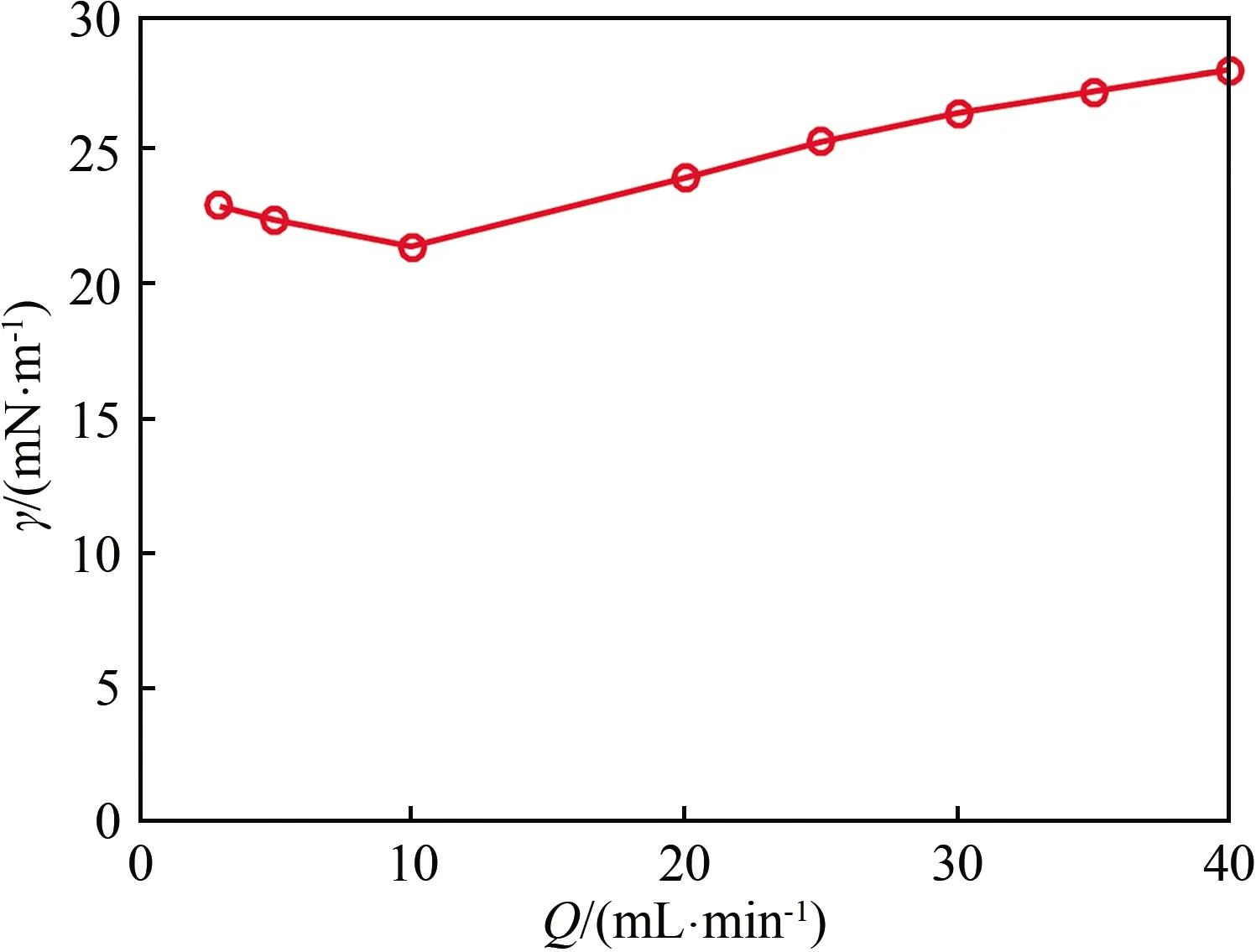
圖4 表面張力系數隨皂液流量的變化

3 皂膜厚度測量

對流動皂膜的厚度場進行測量，無法采用接觸式方法，主要采用光學測量手段，比如利用皂膜對不同波長可見光的干涉[35-36]，或利用皂膜對特定波長紅外輻射的吸收[30,37]。本文提出一種與速度場測量相結合的、基于薄膜干涉的光學測量方法。

如圖5所示，在波長為λ=532 nm的單色激光照射下，流量Q=40 mL/min的皂膜表面形成了明暗相間的干涉條紋。可以發現：干涉條紋基本為豎直條紋，表明皂膜厚度在水平方向的變化遠大于在豎直方向的變化，即，對于豎直方向流動的穩定皂膜，水平方向的質量輸運很弱，厚度在豎直方向上幾乎不變。另外，皂膜邊界幾乎處于同一豎直干涉條紋上，說明其厚度變化很小，由于厚度不同而可能導致的表面張力沿邊界的變化也很小，這也間接支持了前文作出的邊界處表面張力相同的假設。本文忽略豎直方向的皂膜厚度變化，僅分析水平方向的厚度變化造成的干涉現象。

圖5 皂膜表面干涉條紋

圖6為皂膜橫剖面內的光路圖，上、下藍線分別表示z方向的皂膜前后表面。平行光oa和jf以入射角θ1入射至皂膜的前表面af，由于空氣折射率n1和皂液折射率n2不同，入射光在前表面af發生折射及反射；oa的折射光ad到達皂膜的后表面bd后，再次發生折射與反射，考慮其反射光df恰好到達f點，將與入射光jf發生疊加，其結果取決于光線o-a-d-f與j-f的光程差。

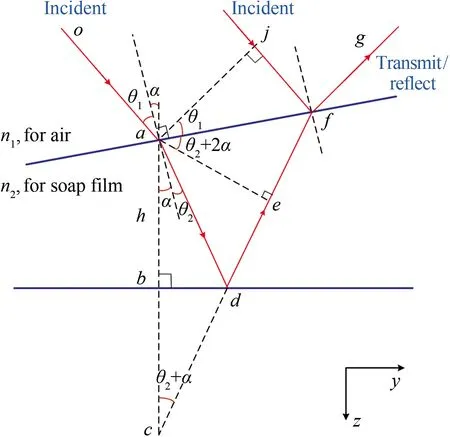
圖6 皂膜橫剖面內的光路圖

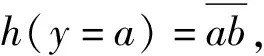
(12)

記光線在a點的折射角為θ2，則：

(13)

(14)

其中，α=arctan(?h/?y)為皂膜外法線與z方向的夾角。將式(13)和(14)代入式(12)，可得：

Δl=2hn2(cosθ2-2sin(θ2+α/2)sin(α/2))

(15)

其中，最后一個等式是基于α≈Δh/Δy≈1×10-4而作的簡化。值得注意的是，當光從低折射率n1的空氣入射到高折射率n2的皂膜中，會發生180°的相位變化[39]，因此，當Δl=(k-0.5)λ,k=1, 2, 3,…時會產生相長干涉，而當Δl=kλ,k=1, 2, 3,…時則會產生相消干涉。

根據式(15)，干涉條紋可以提供沿y方向皂膜厚度的相對變化情況。相鄰的兩個明條紋(暗條紋)光程差為λ，對應的厚度變化為δh=λ/(2n2cosθ2)。假設尼龍繩邊界處皂膜厚度為h(y=0)=h0，則根據流動皂膜的質量守恒可得：

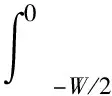
(16)

其中，δh(y)=h(y)-h0為皂膜內部一點處與邊界處的相對厚度，可通過干涉條紋的個數及插值計算得出。因此，對于給定的皂液流量Q，若實驗測得皂膜水平截面上的速度剖面u(y)，則可以通過式(16)確定邊界處的厚度h0，進而獲得皂膜水平方向的厚度剖面h(y)。

采用粒子圖像測速法(Particle Image Velocimetry, PIV)對皂膜的速度場進行測量。在皂液中加入直徑1 μm的聚苯乙烯塑料珠作為流動示蹤顆粒，以重復頻率5000 Hz、功率100 W的高頻高功率脈沖激光照亮示蹤顆粒，通過與激光器同步的高速相機拍攝瞬時顆粒圖像，再采用標準的互相關算法來獲取流動速度剖面u(y)。

圖7為x=0處(即實驗段中心位置)、皂液流量Q=35 mL/min時的皂膜流動速度剖面(僅顯示對稱的右半部分剖面；在表面張力的拉伸作用下，x=0處的皂膜寬度略小于實驗段入口處寬度5 cm，約為4.85 cm)。從圖中可見，皂膜速度在中心處較大，而在靠近邊界處(尼龍繩處)速度較小。

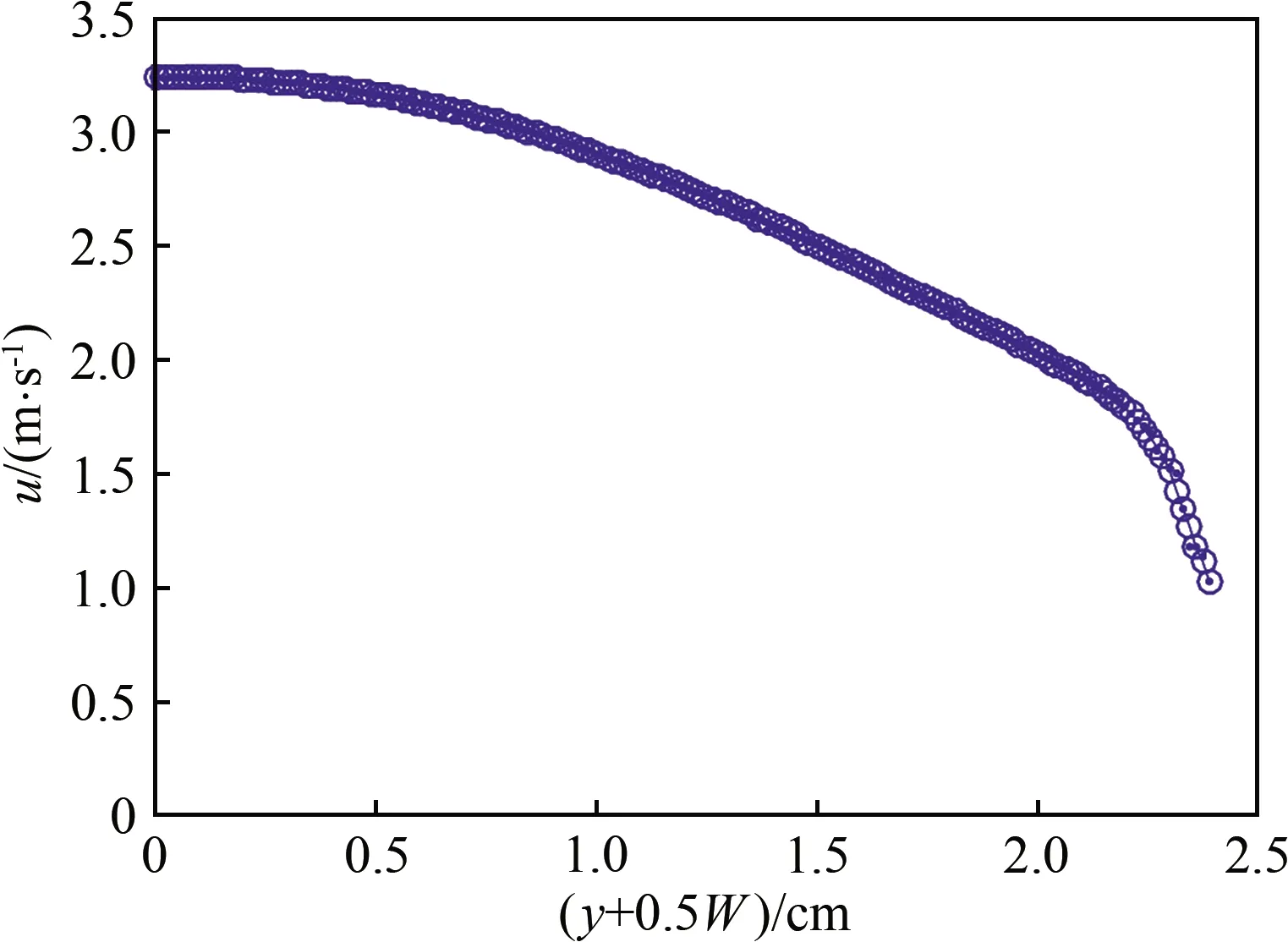
圖7 皂膜流動的速度剖面

根據實測的速度剖面，利用式(15)計算得到的皂膜厚度剖面如圖8所示(僅顯示右半部分剖面)。可以看出，類似于速度剖面，皂膜厚度在中心處較大，向邊界處逐漸變薄。在本文實驗工況下，測得的皂膜內平均速度u=1～4 m/s，皂膜平均厚度h=3～9 μm，這與Wu等[30]針對類似流動皂膜進行測量的結果基本一致。

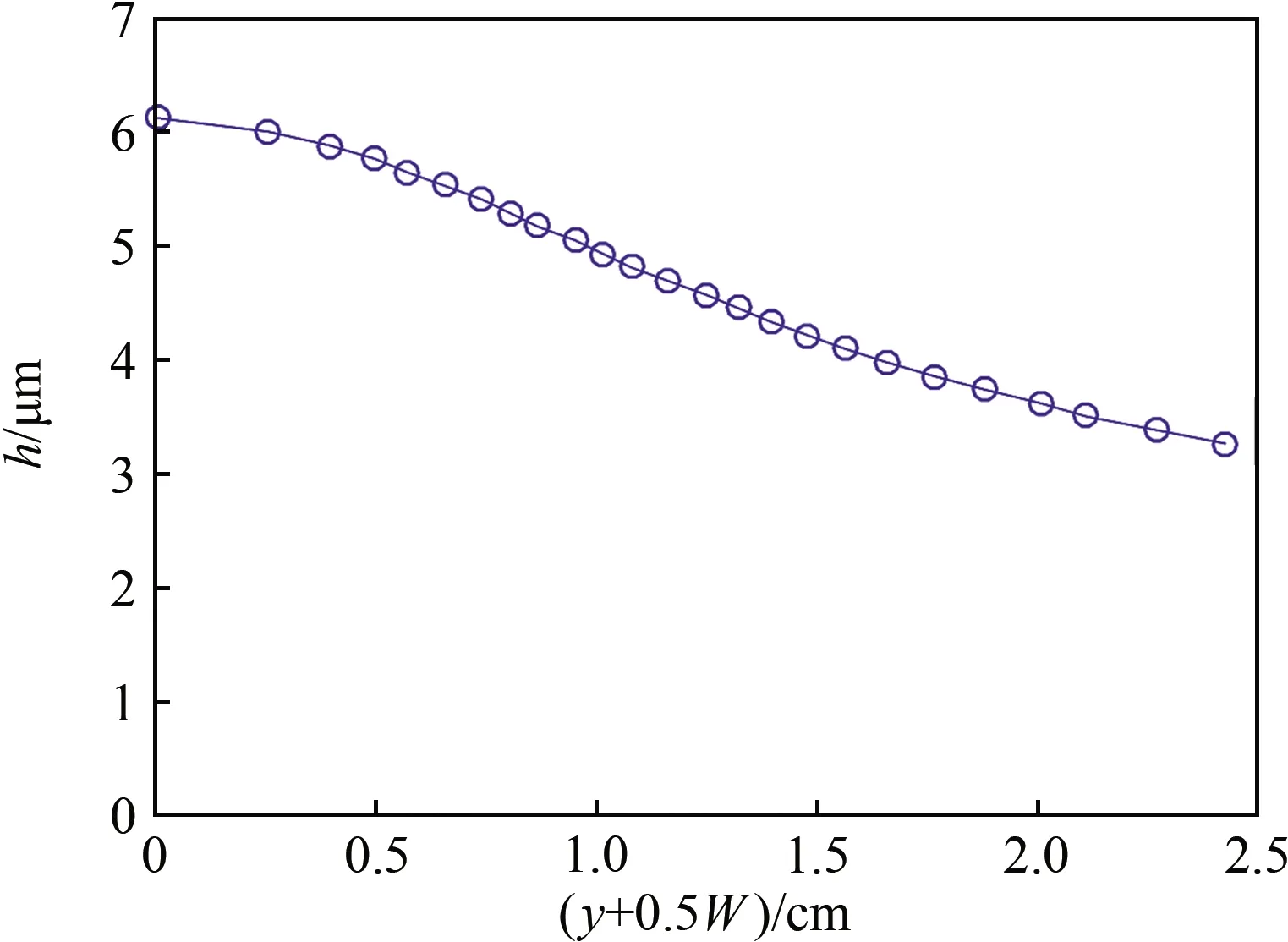
圖8 皂膜流動的厚度剖面

4 結 論

本文搭建了一個重力驅動的平面流動皂膜實驗裝置，能夠得到皂液流量Q=5～60 mL/min、平均速度u=1～4 m/s、平均厚度h=3～9 μm的穩定豎直流動的皂膜。為測量皂膜的表面張力系數，基于皂膜邊界上的力平衡方程推導得到流動皂膜邊界曲線方程的精確解。實驗結果驗證了本文推導，并由此得出表面張力系數的兩種測量方法。此外，還提出了一種基于光學干涉的皂膜厚度測量方法。將該方法與皂膜流動速度剖面測量相結合，可以給出皂膜的厚度剖面。本文中提出的皂膜表面張力系數及厚度的測量方法簡便易行，可以較為全面地測量平面流動皂膜并評估其特性(如擾動波在皂膜中的傳播速度)。