全平衡卷?yè)P(yáng)式垂直升船機(jī)液壓動(dòng)態(tài)調(diào)平下的縱傾穩(wěn)定特性研究*

張 陽(yáng)，石端偉*，肖 童，程熊豪，周 吉

(1.武漢大學(xué) 水力機(jī)械過(guò)渡過(guò)程教育部重點(diǎn)實(shí)驗(yàn)室,湖北 武漢 430072；2.武漢大學(xué) 動(dòng)力與機(jī)械學(xué)院,湖北 武漢 430072)

0 引 言

對(duì)于全平衡卷?yè)P(yáng)式垂直升船機(jī)，在運(yùn)行過(guò)程中，由于提升卷筒圓度、鋼絲繩直徑、鋼絲繩彈性模量制造誤差等因素的影響，承船廂不可避免地會(huì)產(chǎn)生微量縱傾。為了調(diào)平承船廂以及均衡鋼絲繩的拉力，研究人員設(shè)置了液壓調(diào)平子系統(tǒng)。但是，由于液壓調(diào)平子系統(tǒng)啟動(dòng)后會(huì)與主提升子系統(tǒng)、承船廂結(jié)構(gòu)及廂內(nèi)淺水晃動(dòng)子系統(tǒng)構(gòu)成復(fù)雜的機(jī)-液-固-流(MHSF)耦合系統(tǒng)，其動(dòng)態(tài)穩(wěn)定性以及抗承船廂傾覆的能力尚不清楚，目前僅允許液壓靜態(tài)調(diào)平[1-2](升船機(jī)停機(jī)后啟動(dòng)液壓調(diào)平系統(tǒng))。為了在安全運(yùn)行的同時(shí)提高通航效率，研究液壓動(dòng)態(tài)調(diào)平(升船機(jī)運(yùn)行過(guò)程中啟動(dòng)液壓調(diào)平系統(tǒng))下承船廂的縱傾穩(wěn)定性十分必要。

國(guó)內(nèi)針對(duì)卷?yè)P(yáng)式升船機(jī)耦合系統(tǒng)穩(wěn)定性的研究中，阮詩(shī)倫[3]建立了船-水-廂耦合運(yùn)動(dòng)方程，并結(jié)合伽遼金法以及精細(xì)積分法進(jìn)行了時(shí)域計(jì)算；程耿東[4]考慮提升鋼絲繩、平衡重、承船廂、水體和船建立了耦合系統(tǒng)，利用自振頻率為零時(shí)系統(tǒng)失穩(wěn)為判據(jù)研究了穩(wěn)定性。以上研究雖然考慮到了船-水-廂的耦合，但模型中對(duì)于縱傾穩(wěn)定具有關(guān)鍵影響的主提升機(jī)械結(jié)構(gòu)考慮并不完整，尤其缺少了同步軸這一關(guān)鍵結(jié)構(gòu)；廖樂(lè)康[5]率先建立了主提升子系統(tǒng)、承船廂結(jié)構(gòu)與廂內(nèi)水體晃動(dòng)的耦合動(dòng)力學(xué)模型，并利用胡爾維茨定理判定了縱傾穩(wěn)定性；程熊豪[6]在模型中補(bǔ)充了缺少的重力平衡重，并利用笛卡爾準(zhǔn)則推導(dǎo)了臨界吊點(diǎn)中心距計(jì)算公式。

雖然主提升子系統(tǒng)考慮趨于完善，但仍然缺少關(guān)鍵的轉(zhuǎn)矩平衡重，且Housner理論對(duì)廂內(nèi)淺水晃動(dòng)子系統(tǒng)的模擬準(zhǔn)確度有待提高。文獻(xiàn)[7]利用多模態(tài)理論建立了淺水晃動(dòng)子系統(tǒng)模型，完整考慮了主提升子系統(tǒng)與承船廂結(jié)構(gòu)子系統(tǒng)模型，形成了機(jī)械-結(jié)構(gòu)-流體耦合的動(dòng)力學(xué)模型，并利用李雅普諾夫運(yùn)動(dòng)穩(wěn)定性理論判斷了縱傾穩(wěn)定性，研究結(jié)果對(duì)于液壓靜態(tài)調(diào)平下的縱傾穩(wěn)定性分析是適用的，但對(duì)于液壓動(dòng)態(tài)調(diào)平下形成的復(fù)雜MHSF耦合系統(tǒng)價(jià)值有限。

國(guó)內(nèi)針對(duì)液壓調(diào)平子系統(tǒng)的研究中，陸嚴(yán)[8-9]進(jìn)行了比例物理模型試驗(yàn)研究，探索了模糊控制在自動(dòng)調(diào)平問(wèn)題中的適用性；王剛[10]建立了液壓調(diào)平子系統(tǒng)的數(shù)學(xué)模型，提出了基于二分逼近法和積分同步法的承船廂調(diào)平控制策略。以上研究為調(diào)平控制策略提供了很好的參考，但均將液壓調(diào)平子系統(tǒng)作為獨(dú)立不參與耦合的系統(tǒng)進(jìn)行了研究，對(duì)于液壓動(dòng)態(tài)調(diào)平的可行性探索是不利的。彭華偉[11]和潘爾順[12]將液壓調(diào)平子系統(tǒng)簡(jiǎn)化為一階反饋系統(tǒng)，利用動(dòng)態(tài)子結(jié)構(gòu)法實(shí)現(xiàn)了液壓調(diào)平子系統(tǒng)與其他子系統(tǒng)的動(dòng)態(tài)耦合，并求解了動(dòng)態(tài)響應(yīng)。這對(duì)于MHSF耦合系統(tǒng)的研究是一個(gè)很好的嘗試，但對(duì)于液壓調(diào)平子系統(tǒng)的簡(jiǎn)化不利于動(dòng)態(tài)特性的研究。

國(guó)外學(xué)者針對(duì)升船機(jī)的研究主要集中在工程設(shè)計(jì)及施工應(yīng)用層面，對(duì)于升船機(jī)MHSF耦合系統(tǒng)的內(nèi)在機(jī)理性研究尚處于空白。

本文針對(duì)液壓動(dòng)態(tài)調(diào)平下的全平衡卷?yè)P(yáng)式垂直升船機(jī)，首次建立包含主提升子系統(tǒng)、液壓調(diào)平子系統(tǒng)、承船廂結(jié)構(gòu)運(yùn)動(dòng)子系統(tǒng)以及淺水晃動(dòng)子系統(tǒng)的MHSF耦合動(dòng)力學(xué)模型；研究承船廂的縱傾穩(wěn)定性；計(jì)算鋼絲繩臨界吊點(diǎn)中心距；分析各子系統(tǒng)的穩(wěn)定特性及響應(yīng)的快速性。

1 MHSF耦合系統(tǒng)模型

筆者將液壓動(dòng)態(tài)調(diào)平狀態(tài)下的全平衡卷?yè)P(yáng)式垂直升船機(jī)簡(jiǎn)化為二維雙吊點(diǎn)系統(tǒng)，用于探索液壓動(dòng)態(tài)調(diào)平下的承船廂縱傾穩(wěn)定特性。

全平衡卷?yè)P(yáng)式垂直升船機(jī)的MHSF耦合動(dòng)力學(xué)模型圖如圖1所示。

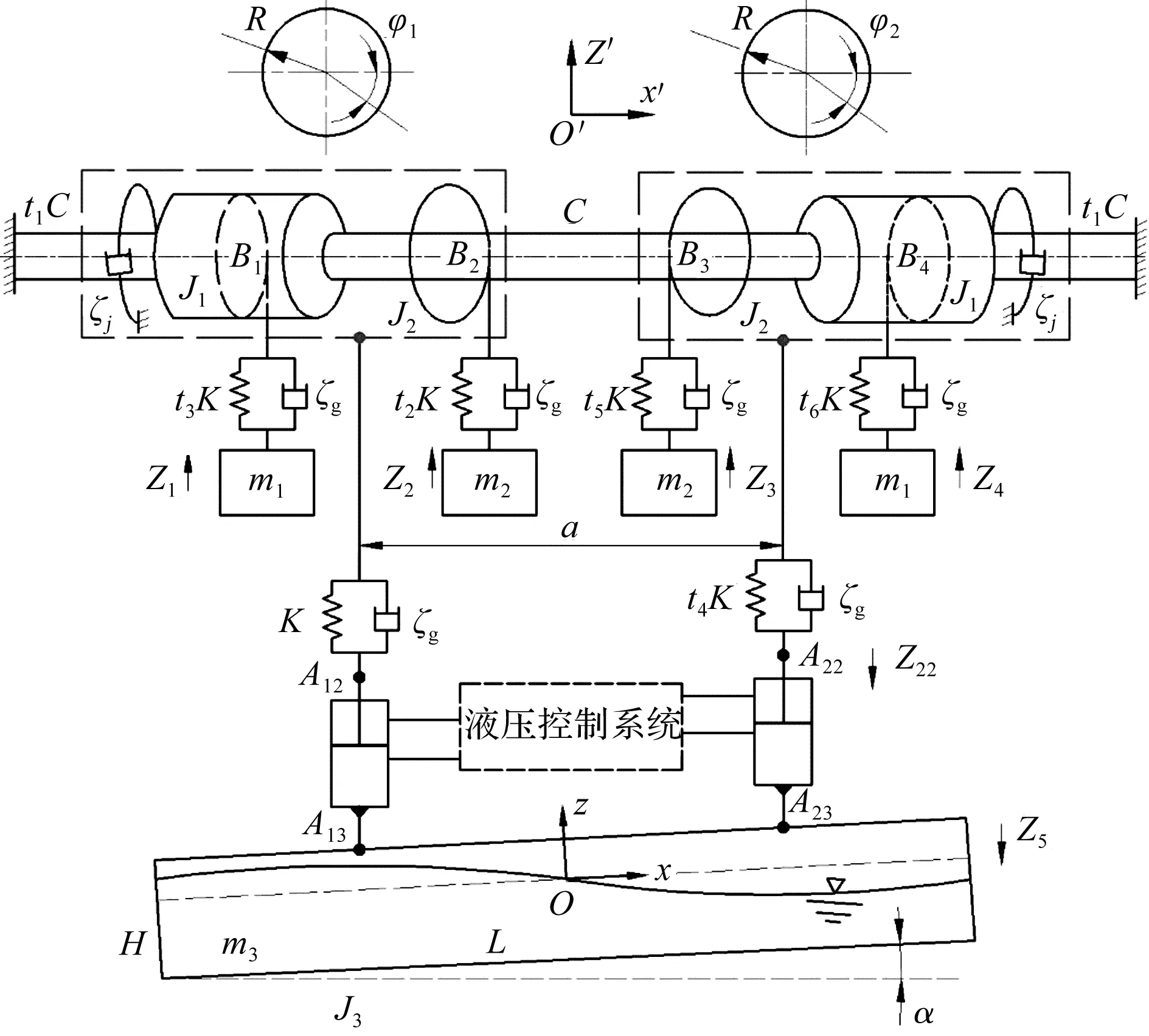
圖1 全平衡卷?yè)P(yáng)式垂直升船機(jī)的MHSF耦合動(dòng)力學(xué)模型R-卷筒和滑輪的半徑；φ1-上游側(cè)卷筒的轉(zhuǎn)動(dòng)角位移；φ2-下游側(cè)卷筒的轉(zhuǎn)動(dòng)角位移；B1-上游側(cè)提升卷筒；B4-下游側(cè)提升卷筒；B2-上游側(cè)滑輪；B3-下游側(cè)滑輪；C-同步軸等效扭轉(zhuǎn)剛度；t1C-電機(jī)傳動(dòng)軸等效扭轉(zhuǎn)剛度；J1-卷筒的等效轉(zhuǎn)動(dòng)慣量；J2-滑輪的等效轉(zhuǎn)動(dòng)慣量；ξj-主提升機(jī)扭轉(zhuǎn)振動(dòng)阻尼比；ξg-鋼絲繩僵性阻尼比；t2K-上游側(cè)重力平衡重懸吊鋼絲繩的等效剛度；t3K-上游側(cè)轉(zhuǎn)矩平衡重懸吊鋼絲繩的等效剛度；t5K-下游側(cè)重力平衡重懸吊鋼絲繩的等效剛度；t6K-下游側(cè)轉(zhuǎn)矩平衡重懸吊鋼絲繩的等效剛度；m1-轉(zhuǎn)矩平衡重的一半；m2-重力平衡重的一半；Z1-上游側(cè)轉(zhuǎn)矩平衡重的位移；Z2-上游側(cè)重力平衡重的位移；Z3-下游側(cè)重力平衡重的位移；Z4-下游側(cè)轉(zhuǎn)矩平衡重的位移；a-鋼絲繩吊點(diǎn)中心距；K-上游側(cè)提升鋼絲繩的等效剛度；t4K-下游側(cè)提升鋼絲繩的等效剛度；A12-上游側(cè)提升鋼絲繩下端與調(diào)平液壓缸的鉸接點(diǎn)；A22-下游側(cè)提升鋼絲繩下端與調(diào)平液壓缸的鉸接點(diǎn)；A13-上游側(cè)調(diào)平液壓缸與承船廂上端的鉸接點(diǎn)；A23-下游側(cè)調(diào)平液壓缸與承船廂上端的鉸接點(diǎn)；z22-調(diào)平液壓缸活塞位移；Z5-承船廂在豎直方向的位移；H-承船廂水深；L-承船廂長(zhǎng)度；m3-承船廂及廂內(nèi)水體的質(zhì)量；J3-承船廂及廂內(nèi)水體的等效轉(zhuǎn)動(dòng)慣量；α-承船廂縱傾運(yùn)動(dòng)角度

1.1 淺水晃動(dòng)子系統(tǒng)模型

根據(jù)文獻(xiàn)[13]，在承船廂縱傾運(yùn)動(dòng)的影響下(見(jiàn)圖1)，廂內(nèi)水體的淺水晃動(dòng)特性及產(chǎn)生的傾覆力矩可以表達(dá)為：

(1)

(2)

式中：M—淺水晃動(dòng)產(chǎn)生的傾覆力矩；β1—淺水晃動(dòng)的一階模態(tài)函數(shù)；ρ—水體密度；ξ1—水體一階邊界層阻尼；ω1—淺水晃動(dòng)一階自振頻率；g—重力加速度。

1.2 液壓調(diào)平子系統(tǒng)模型

當(dāng)承船廂在運(yùn)行過(guò)程中出現(xiàn)圖1所示縱傾時(shí)，水平傳感器將水平偏差信號(hào)傳輸給控制器，控制器發(fā)出控制信號(hào)，經(jīng)比例放大器放大后控制比例調(diào)速閥，經(jīng)比例調(diào)速閥調(diào)節(jié)的液壓油僅進(jìn)入A22側(cè)油缸有桿腔，A12側(cè)油壓不變，推動(dòng)活塞向下運(yùn)動(dòng)，從而調(diào)平承船廂。

液壓調(diào)平子系統(tǒng)主要包括：比例放大器、比例調(diào)速閥、四通閥控非對(duì)稱(chēng)液壓缸和承船廂水平度傳感器。其中，比例放大器工作頻率遠(yuǎn)高于液壓缸及承船廂的工作頻率，簡(jiǎn)化為比例環(huán)節(jié)，即以控制器及D/A轉(zhuǎn)換后的電壓信號(hào)U為輸入，電流I為輸出，傳遞函數(shù)如下：

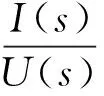
(3)

式中：Kα—比例放大器增益。

比例調(diào)速閥為電氣元件，以電流I為輸入，滑閥閥芯位移xv為輸出，其響應(yīng)速度比較快，與液壓動(dòng)力元件相比，動(dòng)態(tài)特性可以忽略不計(jì)，視為比例環(huán)節(jié)。傳遞函數(shù)為：

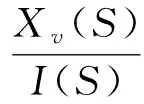
(4)

式中：Ksv—比例調(diào)速閥的流量增益。

四通閥控非對(duì)稱(chēng)調(diào)平液壓缸以閥芯位移xv為輸入，活塞位移z22為輸出。考慮彈性負(fù)載剛度、忽略液壓缸泄漏情況下，四通閥控非對(duì)稱(chēng)液壓缸的傳遞函數(shù)G(s)[14]為：

(5)

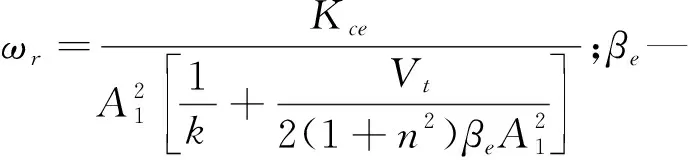
承船廂水平傳感器以水平偏差Lα為輸入，以電壓U′為輸出，傳遞函數(shù)如下：

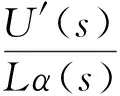
(6)

式中：Kf—傳感器增益。

綜上，液壓調(diào)平子系統(tǒng)閉環(huán)傳遞函數(shù)方框圖如圖2所示。

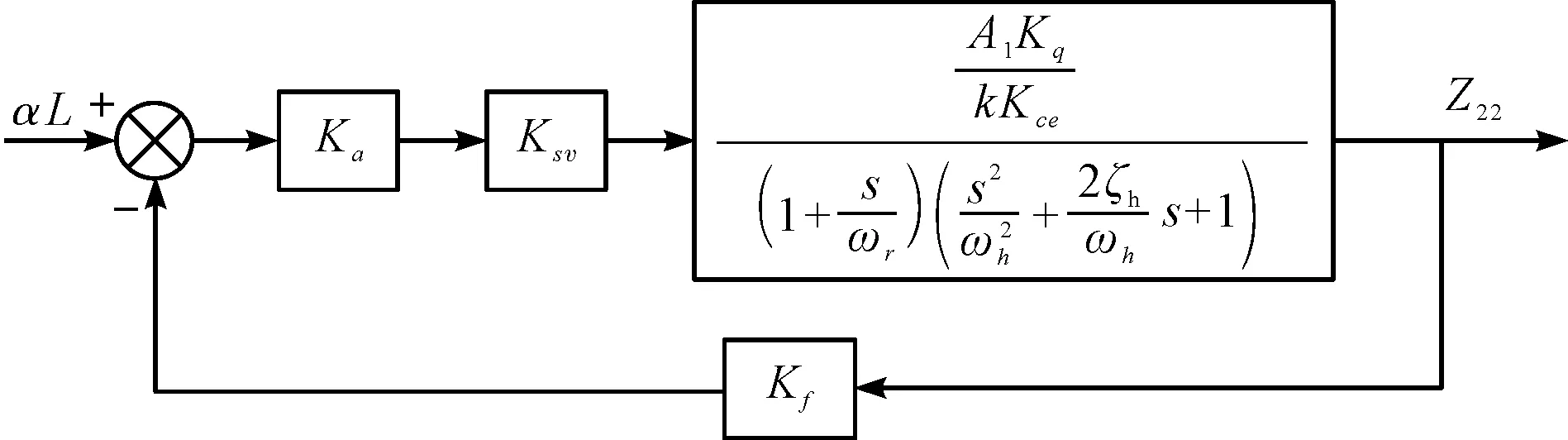
圖2 液壓調(diào)平子系統(tǒng)閉環(huán)傳遞函數(shù)方框圖

由圖2可知，液壓調(diào)平子系統(tǒng)的閉環(huán)傳遞函數(shù)GB(s)為：

GB(s)=

(7)

則，液壓調(diào)平子系統(tǒng)的微分方程為：

(8)

1.3 主提升機(jī)械子系統(tǒng)模型

從圖1可得，主提升機(jī)械子系統(tǒng)和承船廂結(jié)構(gòu)子系統(tǒng)的動(dòng)能與勢(shì)能分別為：

(9)

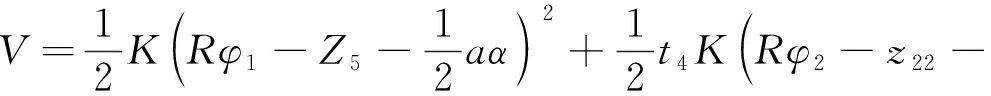
(10)

式中：t1—同步軸與電機(jī)傳動(dòng)軸的扭轉(zhuǎn)剛度比；t2—上游側(cè)重力平衡重懸吊鋼絲繩彈性模量容差和提升揚(yáng)程的影響系數(shù)；t3—上游側(cè)轉(zhuǎn)矩平衡重懸吊鋼絲繩彈性模量容差和提升揚(yáng)程的影響系數(shù)；t5—下游側(cè)重力平衡重懸吊鋼絲繩彈性模量容差和提升揚(yáng)程的影響系數(shù)；t6—下游側(cè)轉(zhuǎn)矩平衡重懸吊鋼絲繩彈性模量容差和提升揚(yáng)程的影響系數(shù)；t4—上、下游側(cè)鋼絲繩之間彈性模量制造誤差的影響系數(shù)。

根據(jù)第二類(lèi)拉格朗日方程可得主提升子系統(tǒng)動(dòng)力學(xué)模型，即：

(11)

(12)

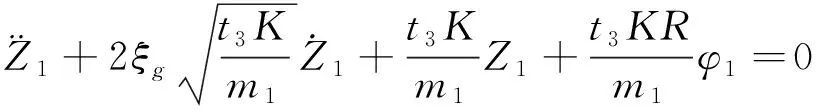
(13)

(14)

(15)

(16)

1.4 承船廂結(jié)構(gòu)子系統(tǒng)模型

結(jié)合式(9～10)，根據(jù)第二類(lèi)拉格朗日方程，可得承船廂結(jié)構(gòu)子系統(tǒng)的動(dòng)力學(xué)方程，即：

(17)

(18)

式中：ξp—升船機(jī)承船廂縱傾運(yùn)動(dòng)阻尼比；ξv—升船機(jī)承船廂豎向運(yùn)動(dòng)阻尼比。

1.5 MHSF耦合系統(tǒng)動(dòng)力學(xué)模型

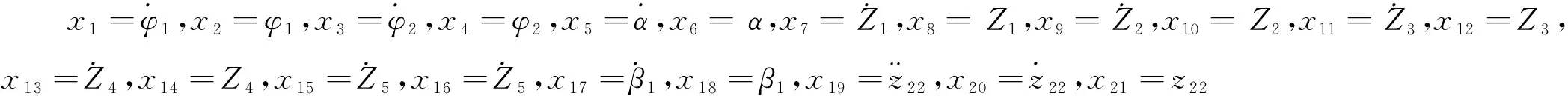
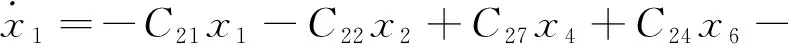
(19)

(20)

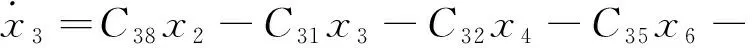
(21)

(22)

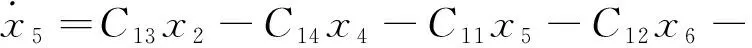
(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

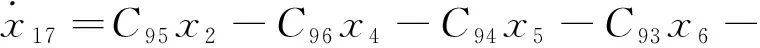
(35)

(36)

(37)

(38)

(39)

式中：Cij—式(1～2，8，11～18)化簡(jiǎn)為式(19～39)過(guò)程中，各參數(shù)前的系數(shù)表達(dá)式。

2 臨界吊點(diǎn)中心距計(jì)算

臨界吊點(diǎn)中心距是指耦合系統(tǒng)臨界穩(wěn)定狀態(tài)下對(duì)應(yīng)的吊點(diǎn)中心距，是評(píng)價(jià)縱傾穩(wěn)定性的重要指標(biāo)；臨界吊點(diǎn)中心距越小說(shuō)明穩(wěn)定性越高。

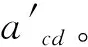
通過(guò)兩種不同方法計(jì)算得到的四座典型全平衡卷?yè)P(yáng)式垂直升船機(jī)不同工況的臨界吊點(diǎn)中心距，如表1所示。

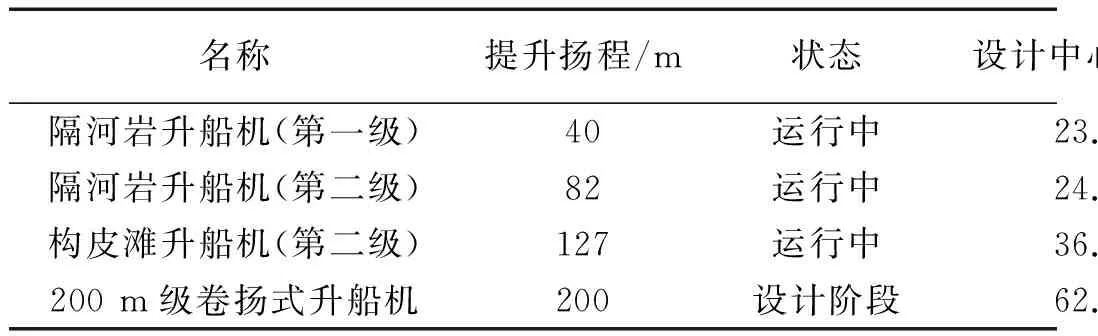
表1 四座典型全平衡卷?yè)P(yáng)式垂直升船機(jī)不同工況的臨界吊點(diǎn)中心距

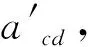
(2)表1中，acs為液壓靜態(tài)調(diào)平下保持縱傾穩(wěn)定對(duì)應(yīng)的臨界吊點(diǎn)中心距；比較acd與acs可以看出，相比較于液壓靜態(tài)調(diào)平，液壓動(dòng)態(tài)調(diào)平會(huì)降低承船廂的縱傾穩(wěn)定性。主要原因是液壓調(diào)平系統(tǒng)以串聯(lián)的方式耦合進(jìn)入原機(jī)械-結(jié)構(gòu)-流體系統(tǒng)，降低了系統(tǒng)的整體剛度；

(3)將acd與設(shè)計(jì)中心距作比較可以看出，在液壓動(dòng)態(tài)調(diào)平下，四座卷?yè)P(yáng)式升船機(jī)的設(shè)計(jì)吊點(diǎn)中心距均依然能夠保證升船機(jī)承船廂處于縱傾穩(wěn)定狀態(tài)。尤其是對(duì)于200 m級(jí)升船機(jī)，設(shè)計(jì)參數(shù)可以保證即使在最危險(xiǎn)位置開(kāi)啟動(dòng)態(tài)調(diào)平，安全系數(shù)依然有1.1(62/56)，承船廂仍然能夠穩(wěn)定安全運(yùn)行。

3 縱傾穩(wěn)定特性分析

3.1 子系統(tǒng)穩(wěn)定特性分析

吊點(diǎn)中心距a=56 m時(shí)，200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)圖如圖3所示。

分析圖3可知，吊點(diǎn)中心距取臨界值56 m時(shí)，淺水晃動(dòng)子系統(tǒng)響應(yīng)呈現(xiàn)等幅振蕩，為臨界穩(wěn)定狀態(tài)；其余各子系統(tǒng)收斂，處于穩(wěn)定狀態(tài)。即淺水晃動(dòng)子系統(tǒng)是最易受吊點(diǎn)中心距影響，而不穩(wěn)定的。

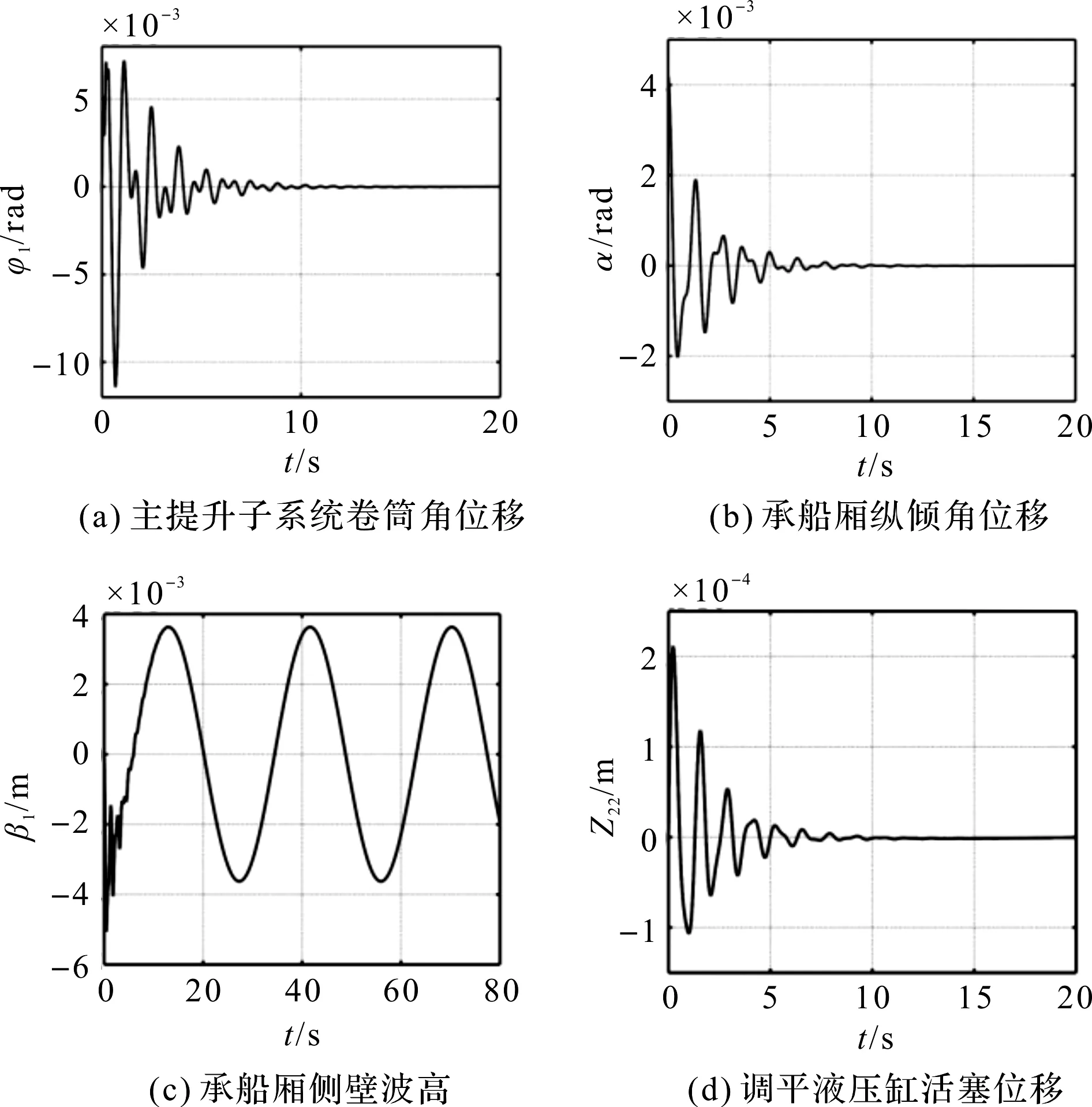
圖3 a=56 m時(shí)200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)

吊點(diǎn)中心距a=19 m時(shí)，200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)圖如圖4所示。

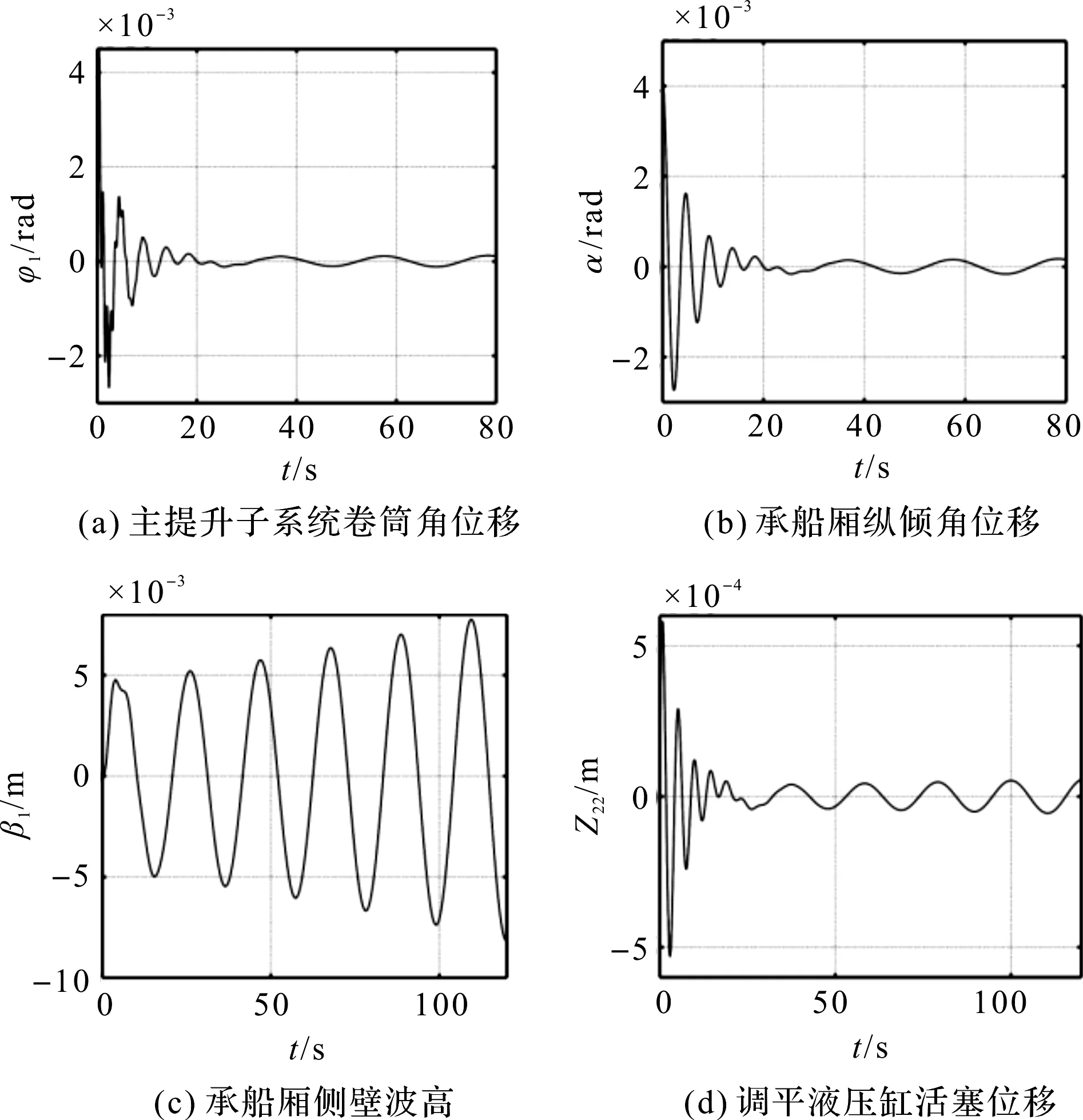
圖4 a=19 m時(shí)200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)

分析圖4可知，當(dāng)?shù)觞c(diǎn)中心距降至19 m時(shí)，淺水晃動(dòng)子系統(tǒng)已經(jīng)發(fā)散，其余各子系統(tǒng)位移響應(yīng)呈現(xiàn)等幅振蕩，處于臨界穩(wěn)定。此時(shí)雖然MHSF耦合系統(tǒng)已經(jīng)縱傾不穩(wěn)定，但懸吊的承船廂不會(huì)出現(xiàn)傾覆。

吊點(diǎn)中心距a=18.5 m時(shí)，200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)圖如圖5所示。

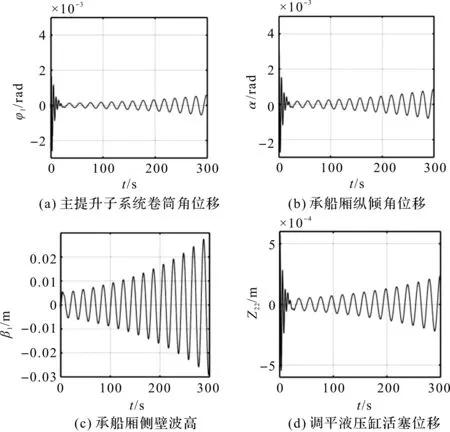
圖5 a=18.5 m時(shí)200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)

圖5中，若吊點(diǎn)中心距低于19 m時(shí)(取18.5 m)，處于臨界穩(wěn)定的主提升子系統(tǒng)、承船廂結(jié)構(gòu)子系統(tǒng)以及液壓調(diào)平子系統(tǒng)的位移響應(yīng)會(huì)慢慢趨于發(fā)散；出現(xiàn)大幅度不可逆傾覆所需的時(shí)間隨吊點(diǎn)中心距的降低而縮短。

3.2 子系統(tǒng)響應(yīng)快速性分析

以200 m級(jí)卷?yè)P(yáng)式垂直升船機(jī)為對(duì)象，根據(jù)工程實(shí)際，給定初始狀態(tài)縱傾角0.004 2 rad。

吊點(diǎn)中心距a=62 m時(shí)，200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)圖如圖6所示。

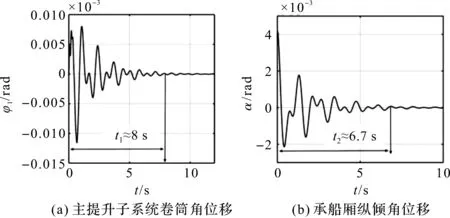
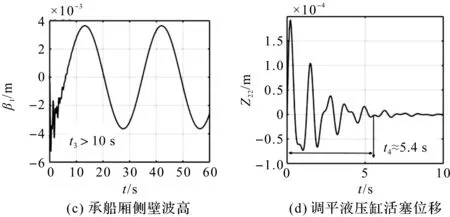
圖6 a=62 m時(shí)200 m級(jí)升船機(jī)各子系統(tǒng)位移響應(yīng)

圖6中，t1～t4分別表示對(duì)應(yīng)各子系統(tǒng)從開(kāi)始響應(yīng)到進(jìn)入工程誤差允許范圍內(nèi)的穩(wěn)態(tài)所需的調(diào)整時(shí)間。由圖6可知，淺水晃動(dòng)子系統(tǒng)的響應(yīng)快速性是最差的(t3>10 s)；其次就是主提升系統(tǒng)(t1≈8 s)；再是承船廂結(jié)構(gòu)子系統(tǒng)(t2≈6.7 s)；響應(yīng)快速性最好的是液壓調(diào)平子系統(tǒng)(t4≈5.4 s)。

4 結(jié)束語(yǔ)

為研究全平衡卷?yè)P(yáng)式垂直升船機(jī)承船廂在液壓動(dòng)態(tài)調(diào)平下的縱傾穩(wěn)定性，本文建立了包含主提升機(jī)械子系統(tǒng)、液壓調(diào)平子系統(tǒng)、承船廂結(jié)構(gòu)子系統(tǒng)與淺水晃動(dòng)子系統(tǒng)的MHSF耦合動(dòng)力學(xué)模型；利用變步長(zhǎng)龍格庫(kù)塔法求解時(shí)間響應(yīng)，以響應(yīng)的收斂性為判據(jù)得到了臨界吊點(diǎn)中心距；以四座典型全平衡卷?yè)P(yáng)式升船機(jī)為例，驗(yàn)證了模型及方法的可靠性；分析了各子系統(tǒng)的穩(wěn)定特性與響應(yīng)快速性。

研究結(jié)果表明：

(1)對(duì)于全平衡卷?yè)P(yáng)式垂直升船機(jī)，與液壓靜態(tài)調(diào)平相比，液壓動(dòng)態(tài)調(diào)平雖然會(huì)降低縱傾穩(wěn)定安全裕度，但依然能夠保證承船廂運(yùn)行過(guò)程中始終處于縱傾穩(wěn)定狀態(tài)；

(2)對(duì)于200 m級(jí)卷?yè)P(yáng)式垂直升船機(jī)，在液壓動(dòng)態(tài)調(diào)平狀態(tài)下，目前的設(shè)計(jì)中心距62 m可以保證縱傾穩(wěn)定安全系數(shù)不低于1.1；即使設(shè)計(jì)吊點(diǎn)中心距略低于臨界值56 m，水體晃動(dòng)緩慢趨于發(fā)散，但承船廂依然能夠維持運(yùn)行；只有設(shè)計(jì)吊點(diǎn)中心距低于19 m時(shí)，承船廂才會(huì)出現(xiàn)傾覆；

(3)200 m級(jí)卷?yè)P(yáng)式垂直升船機(jī)承船廂受到縱傾影響后，各子系統(tǒng)響應(yīng)調(diào)整至穩(wěn)態(tài)的速度由快到慢依

次為：液壓調(diào)平子系統(tǒng)、承船廂結(jié)構(gòu)子系統(tǒng)、主提升子系統(tǒng)、淺水晃動(dòng)子系統(tǒng)。