基于改進型陷波器的伺服系統諧振抑制研究*

龔文全，曾岳南，黃之鋒，郭富強

(廣東工業大學 自動化學院，廣東 廣州 511400)

0 引 言

在交流伺服系統中，伺服電機一般需要通過滾珠絲杠副、聯軸器或者齒輪等機械傳動機構來驅動負載，這些機械傳動環節本身存在著一定的柔性，傳動柔性會導致伺服系統發生機械諧振[1]。諧振發生時電機電流發生震蕩，電機速度控制失準，不僅會產生噪聲，還會對機械傳動環節造成破壞，甚至出現斷軸等后果[2]。添加濾波器是常采用的抑制方法，但是濾波器會產生相位損失，減小系統的相位裕度，導致系統的動態性能變差，甚至失去穩定[3]。

為了改善使用陷波濾波器帶來的相位滯后影響，國內外學者在陷波器結構以及控制策略方面做了大量研究。文獻[4]提出了ZPNF(zero-phase notch filter)的設計方案，減小了陷波器帶來的相位滯后，提高了工業機械手臂的定位快速性；文獻[5]提出了一種新型的ZPNF，對位置控制信號進行了預處理濾波，實驗結果表明，機械手臂的末端抖動得到了抑制，同時跟蹤性能也得到了提高；文獻[6]在ZPNF基礎上，提出了ZPETC(zero phase error tracking controller)方案，將二者有效結合，以提高機械手臂的控制性能，最后在仿真中得到了驗證；文獻[7]針對機械臂的定位和位置跟蹤，提出了一種陷波濾波器的小相位誤差補償策略，提高了機械臂的跟蹤性能。

但這些設計大多是針對伺服系統位置環路的控制，而且零相位陷波器設計復雜。而對于如何在常規二階陷波器的基礎上，減小陷波器帶來的速度環路控制延時，提高速度響應的快速性方面，卻很少有詳細的研究。

針對伺服系統速度環路中，使用常規二階陷波濾波器產生的相位損失問題，本文首先建立柔性負載伺服系統諧振模型；然后對常規二階陷波濾波器的相位特性進行分析，為改善系統的相位穩定裕度，提出一種改進型陷波濾波器，并且在Simulink中建立模型，對所提方法進行仿真分析；最后搭建柔性負載伺服系統實驗平臺，對比改進型陷波器和常規陷波器的抑制效果。

1 柔性伺服系統建模及諧振分析

在交流伺服系統中，電機與負載之間常采用傳動軸、滾珠絲杠副或者聯軸器等傳動機構進行連接。然而傳動機構并不是理想剛性的，電機和負載之間屬于柔性連接。

在分析伺服機械諧振問題的時候，常將柔性伺服系統簡化為二質量模型來分析。一個典型二質量模型如圖1所示。

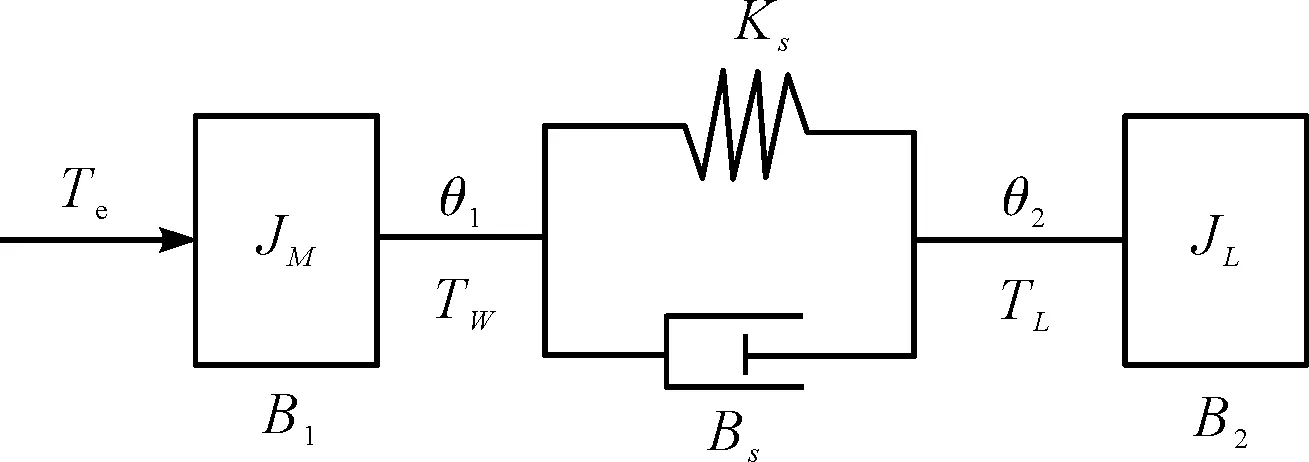
圖1 典型二質量模型

根據以上關系，建立微分方程組：

(1)

式中：Ks—剛度系數；Bs—阻尼系數；Jm—電機轉動慣量；JL—負載轉動慣量；B1—電機轉軸阻尼；B2—負載阻尼；θ1—電機轉角；θ2—負載轉角；Te—電機電磁轉矩；Tw—彈性連接轉矩；TL—負載轉矩。

若忽略阻尼系數，對系統模型進行化簡，對系統微分方程組再進行拉普拉斯變換，可推導出電機轉速同電磁轉矩之間的傳遞函數：

(2)

對式(2)進行整理可得：

(3)

將式(3)的共軛零點稱為抗諧振頻率點ωARF，共軛極點稱為自然振動頻率點ωNTF。

共扼零點為:

(4)

共軛極點為:

(5)

式(3)的諧振方程中，存在一對共軛極點，并且這對共軛極點與虛軸非常接近，這樣會導致系統處于欠阻尼或者臨界振蕩的狀態，一旦有對應頻率的激勵信號，系統的穩定狀態很容易被破壞，這在伺服系統中被稱為機械諧振，表現為電機轉速出現大幅度震動。

2 陷波濾波器的分析和改進

2.1 陷波器抑制諧振原理

考慮理想陷波濾波器的數學表達式為：

(6)

理想的陷波濾波器能夠將輸入信號中的指定頻率成分完全濾除，其中ω0為陷波濾波器的陷波中心頻率。常采用的二階陷波濾波器具有一定的陷波頻帶，只在陷波中心頻率附近提供較大的幅值衰減，而對陷波頻帶外的頻率信號幾乎沒有影響，即：

(7)

式中：kdep—深度系數；Q—寬度系數。

柔性伺服系統發生諧振現象，是因為有信號激勵了系統中存在的諧振點。因此,可以利用陷波濾波器的頻率特性，將陷波濾波器串入速度回路，濾除電流中的諧振頻率激勵信號，抑制電磁轉矩震蕩，從而實現電機轉速諧振抑制。

對于二質量諧振系統，存在單個的諧振頻率，使得該頻率點對應的系統響應急劇增大，破壞系統的穩定性。作為濾波器的一種，陷波濾波器可以在諧振頻率初進行精準的濾波，衰減諧振信號，因此，加入適當的陷波濾波器之后，諧振點峰值會被抑制。

2.2 陷波器的相位影響

陷波器實現了系統諧振峰值的抑制，但是考慮到濾波器本身的相位延遲，也必然會對系統產生一定的相位滯后，使系統的響應變慢，相位穩定裕度減小。

相位穩定裕度表征一個系統的穩定性能，通常用來判斷系統是否穩定的依據為：

PM=180°+φ(ω)

(8)

根據自動控制原理可知，對于一個穩定系統而言，其相位裕度至少應保持PM>45°。

對于式(7)，令s=jω，則有：

(9)

其相角特性表達式為：

(10)

所以，陷波濾波器所產生的相角損失為：

(11)

由式(11)可知：若要減小相角損失Δφ(jω)，可以通過減小φ(0)或者增大φ(jω)實現；但對于陷波濾波器來說，改變φ(0)很難實現，所以只能考慮增大φ(jω)。φ(jω)由兩部分組成，分別是分子部分和分母部分，為了方便表示，以下表述中，分別以分子N和分母D來代替。

2.3 改進型陷波濾波器

引入修正因子ε，當ε=1時，即為原陷波濾波器形式，相位特性無改變。當ε>1時，考慮反正切函數特性，由于ε>1且位于分母，此時分子N部分保持不變，分母D部分減小，φ(jω)總體增大，在φ(0)保持不變的情況下，相角損失Δφ(jω)整體變小。

根據上述分析，式(7)可改寫為：

(12)

引入修正因子后，陷波器結構發生改變，可能引起陷波濾波器的陷波深度變化，影響陷波效果。

式(12)中幅值為：

(13)

當ω=ωn時，此時對應最大衰減倍數為：

(14)

則可以得到中心陷波深度為：

D=20lg|H(jω)|

(15)

當ε=1時，即為常規陷波器，其最大衰減倍數為：

|H(jω)|=1-kdep

(16)

取ε=1.5，改進前后陷波器幅頻特性如圖2所示。

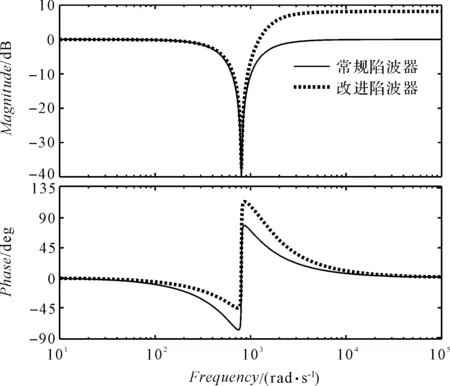
圖2 改進前后陷波器幅頻特性

從圖2中可以看出，常規陷波器的陷波深度約為-40 dB，改進后的陷波器深度為-37.8 dB，約減小2 dB；但是在陷波中心頻率處，常規陷波器的Δφ(jω)=-75.2°，而改進后陷波器為Δφ(jω)=-43.5°，相角損失明顯減小。

所以，改進型陷波器以較小的陷波深度損失，獲得了較大的相位補償，在不影響諧振抑制效果的情況下，系統相位裕度增加。

將兩種陷波器加入諧振系統之后，諧振系統及抑制效果如圖3所示。

圖3 諧振系統及抑制效果

系統開環時，在諧振頻率附近使用常規陷波器時，系統相位約為-130°，使用改進型陷波器系統相位約為-110°，相位滯后更小。另根據式(7)的系統穩定性判據可知，改進型陷波器系統的相位裕度約為70°左右，此時開環系統處于穩定狀態。

在系統閉環狀態，速度環帶寬ωc主要受到抗諧振頻率點ωANF的影響，且ωc<ωARF[8]，閉環系統幅頻特性如圖4所示。

圖4 閉環系統幅頻特性

圖4中，系統的ωARF=285 rad/s，使用常規型陷波器時，速度環帶寬ωc-notch=209 rad/s，使用改進型陷波器時，速度環帶寬ωc-im-notch=220 rad/s。可以看出，相比常規型陷波器，使用改進型陷波器后，系統帶寬增大。

在改進型陷波濾波器的高頻部分，即頻率大于陷波中心頻率處，改進型陷波器的幅頻特性發生了變化，理想狀態下應保持無增益的狀態受到影響，此處的增益被抬高。但是對于中高頻段的伺服系統機械諧振來說，諧振頻率通常處于接近或者超過速度環截止頻率的范圍。

在圖4中，系統閉環的速度環截止頻率為ωc-im-notch=220 rad/s，經過速度環截止頻率的限制之后，高頻信號等于受到了低通濾波器濾波效果，在高峰值的諧振頻率被抑制的前提下，其余的高頻信號被低通濾波效果大幅度衰減，抵消了陷波器所產生的增益抬高。所以，在陷波中心頻率之后，改進型陷波器幅值增益被抬高的特性變化，并不會導致系統出現不穩定狀態。

3 仿真驗證和分析

為了驗證改進型陷波器的有效性，筆者在Simulink中搭建柔性永磁同步電機雙閉環調速系統仿真模型，仿真參數如表1所示。

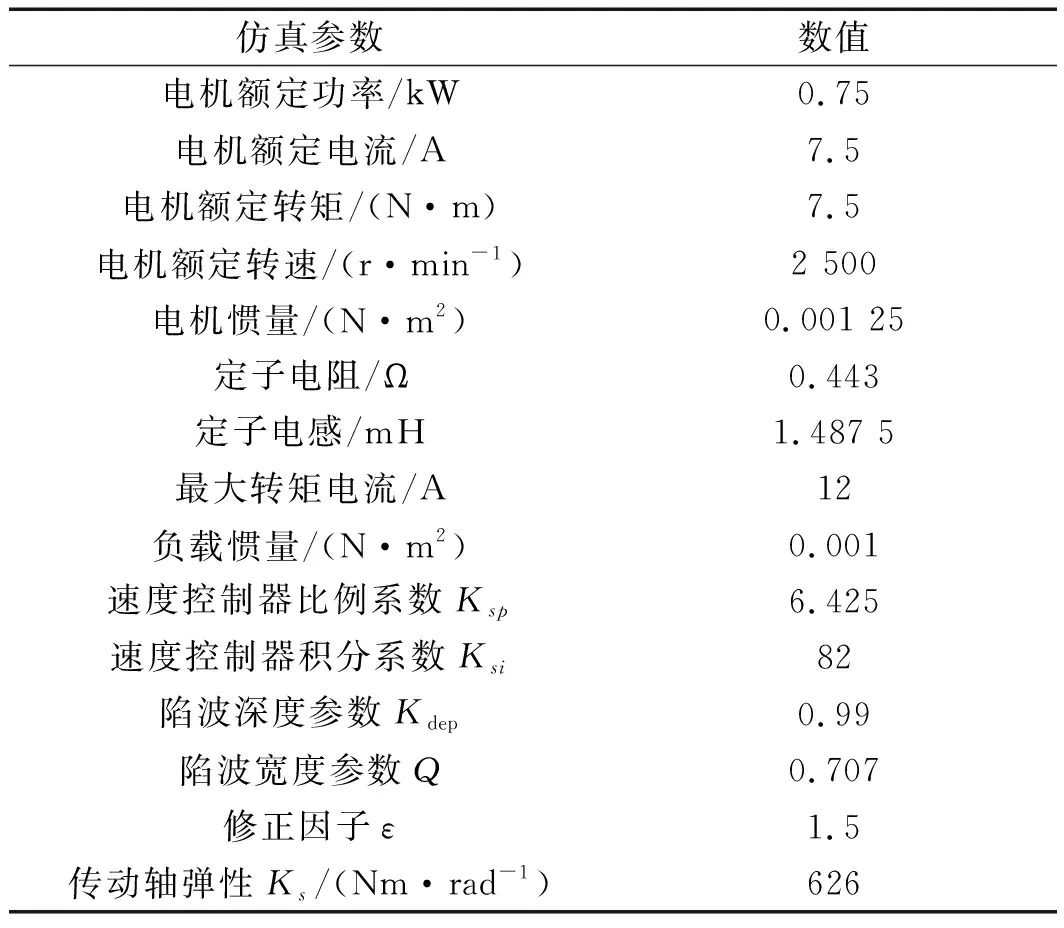
表1 仿真參數

速度給定為130 r/min，使伺服系統發生機械諧振，筆者使用PowerGrid中的FFT分析工具，得到諧振頻率，并以此作為陷波濾波器的中心頻率。

對比無陷波處理的電機轉速和使用常規陷波濾波器的電機轉速，常規陷波器諧振抑制如圖5所示。

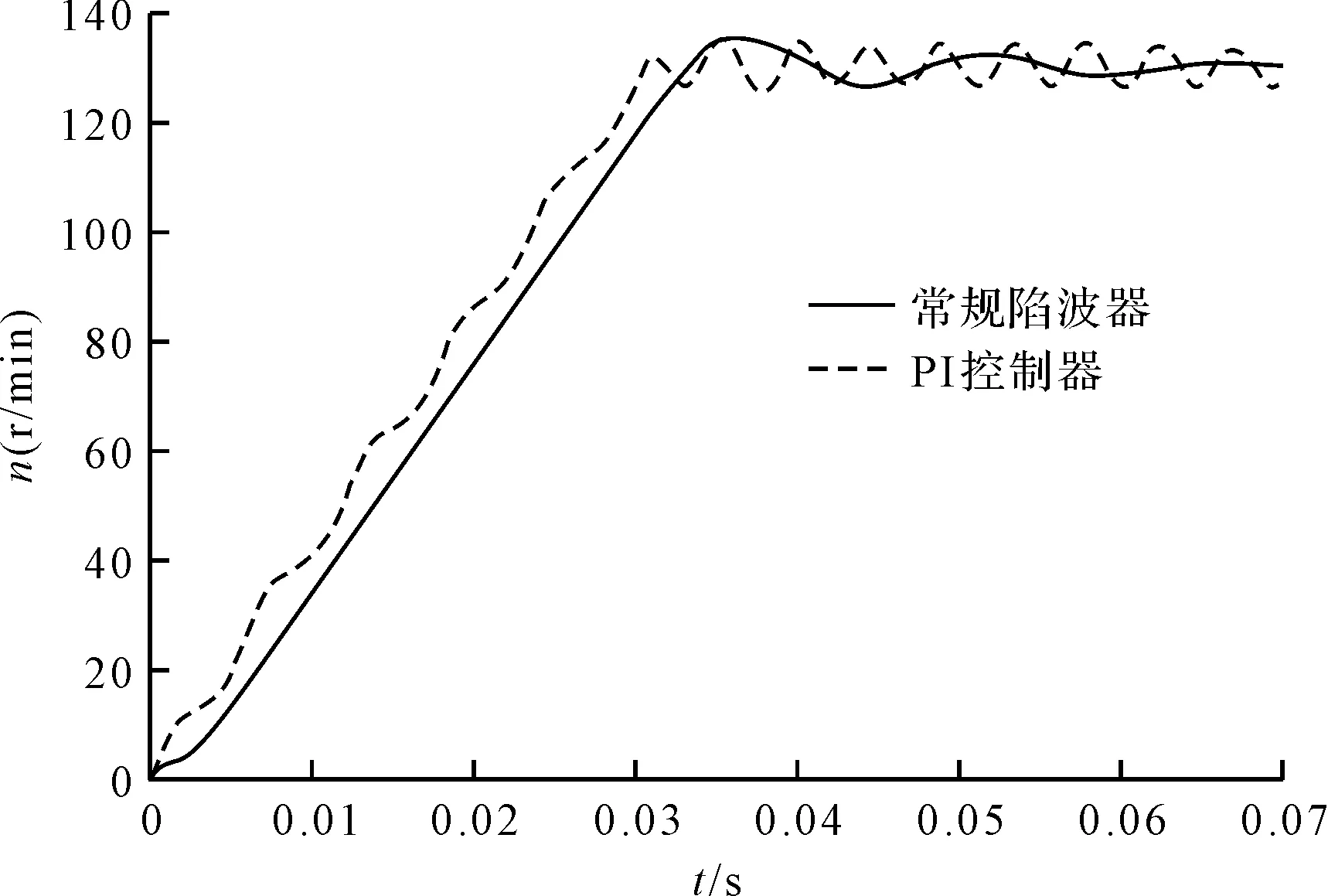
圖5 常規陷波器諧振抑制

從圖5可以看出，當伺服系統發生機械諧振時，如果僅使用PI控制器，電機轉速出現持續震蕩，并且無法收斂；加入常規陷波濾波器之后，電機轉速基本呈現平穩狀態，最終穩定在速度給定值，震蕩得到抑制。

但是通過對比還可以發現，雖然使用陷波濾波器實現了電機轉速振動抑制，然而此時系統的動態響應存在著明顯的滯后現象。

對比使用常規陷波濾波器的電機轉速響應和使用改進型陷波濾波器的電機轉速響應，改進型陷波器抑制效果如圖6所示。

圖6 改進型陷波器抑制效果

從圖6可以看出，兩種陷波器均能實現機械諧振抑制，電機轉速都能夠平穩收斂。但是與常規陷波器相比，經過改進之后，系統的動態性能得到了改善，響應速度明顯提高，而且穩定速度明顯加快。

兩種陷波策略動態性能指標如表2所示。

表2 兩種陷波策略動態性能指標

通過表2可以看出，由于改進型陷波濾波器的相位損失更小，對系統產生的滯后也更小，電機轉速上升時間加快，峰值變小，超調量減小，調節時間更短，速度穩定更快。由此可見，與常規陷波的抑制效果相比，使用改進型陷波器后，系統的動態性能得到了改善。

4 實驗及分析

為驗證所述方法的可行性和有效性，筆者搭建永磁同步電機柔性負載伺服系統。

整個系統由數字式交流伺服驅動單元、表貼式永磁同步電機以及柔性負載等3部分組成，實驗平臺如圖7所示。

圖7 實驗平臺

筆者通過NI公司的模塊化平臺以及LabView工具，顯示電機速度，并且根據電機反饋速度信息，離線獲取速度振動的FFT頻率檢測結果。

實驗控制參數如表3所示。

表3 實驗控制參數

4.1 穩態抑制效果驗證

由于修正因子會導致陷波深度減小，首先驗證在系統發生機械諧振時，改進型陷波濾波器能否實現諧振抑制。

在高控制增益情況下，電機轉速發生劇烈震蕩，筆者于中途加入改進型陷波濾波器，電機轉速抑制前后對比如圖8所示。

圖8 電機轉速抑制前后對比

抑制前電機震蕩幅值接近70 r/min，添加陷波濾波器之后，電機轉速震蕩被迅速抑制，最終保持在4 r/min之內，衰減比例達到94.3%，基本實現平穩輸出，表明改進型陷波器可以實現諧振抑制。

4.2 動態性能對比

保持實驗參數不變，令系統產生諧振，筆者分別在零時刻加入常規陷波器和改進型陷波器，電機轉速動態性能對比如圖9所示。

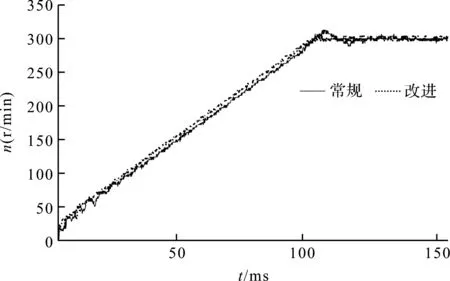
圖9 電機轉速動態性能對比

圖9中，由于改進型陷波器帶來的相位損失更小，造成的相位裕度損失比常規陷波器要更小，系統的穩定性更好，兩種陷波器都可以避免系統發生諧振，使速度波動保持在4 r/min之內。但常規陷波器系統在啟動階段波動幅度較大，而改進型陷波器系統則基本平穩上升。

另外，常規陷波器系統的響應速度較慢，在輸入指令為300 r/min時，速度響應超調接近12 r/min，進入最終穩定需要一段時間。但是改進型陷波器響應速度更快，幾乎無超調，到達輸入指令后，迅速進入穩定狀態，整體動態性能優于常規陷波器系統。

5 結束語

針對彈性傳動環節導致的伺服系統出現機械諧振的問題，本文在完成諧振機理分析的基礎上，提出了一種使用改進型陷波濾波器進行機械諧振抑制的方法，以減小陷波器引入的相位滯后，并實現諧振抑制。

具體過程如下：

(1)對常規型陷波濾波器相位特性進行了分析，并且闡述了引入陷波濾波器之后，對系統相位裕度造成的影響；

(2)提出了改進型陷波濾波器，通過調整校正因子，可以實現陷波器的相位優化，并且保證陷波器的陷波效果；

(3)仿真結果表明:和常規陷波濾波器相比，改進型陷波濾波器的相角損失更小，系統的閉環帶寬得到提升，系統轉速輸出的動態性能更好。實驗結果表明:電機轉速的快速性得到提高，超調量減小。