基于模型參考自適應的一類二維系統形狀漸近跟蹤控制
陳文力 湯曉 王銀河


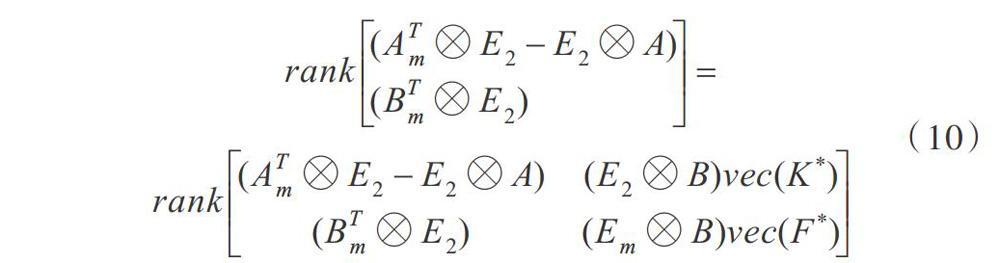
摘要:針對二維線性系統,探究可實現其狀態軌跡形狀與參考系統狀態軌跡間形狀漸近跟蹤的控制方法.首先,利用剛體運動描述系統狀態軌跡的形狀漸近跟蹤概念,然后對傳統模型匹配條件進行擴展。在該條件下,采用Lyapunov穩定性與模型參考自適應相結合的方法,設計形狀漸近跟蹤控制器。實驗表明,該控制器可保證被控系統與參考系統狀態軌跡達到形狀漸近跟蹤。與傳統方法相比,所給出的模型匹配條件及形狀漸近跟蹤控制器適用范圍更廣。最后,對模型進行仿真實驗,證明了該控制方法的有效性。
關鍵詞:自適應控制;線性系統;形狀漸近跟蹤控制器
DOI:10.11907/rjdk.192355 開放科學(資源服務)標識碼(OSID):
中圖分類號:TP301文獻標識碼:A 文章編號:1672-7800(2020)006-0070-04
0 引言
形狀是一個描述曲線彎曲輪廓的幾何概念,近年來,形狀的概念廣泛應用于自然科學及工程實踐中,取得了許多有價值的研究成果。文獻對形狀描述及形狀匹配在計算機視覺領域的應用進行了討論;文獻在仿真人臉皺紋模型中,將形狀函數應用于人臉皺紋模型;文獻針對一類仿射非線性系統,探究了非線性動態權值約束的最優概率密度函數控制問題,基于對概率密度函數形狀的控制,提出了一種最優概率密度函數控制方法。由此可以看出,利用形狀概念研究工程問題具有重要的理論和實踐意義。
在控制理論研究中,形狀通常作為描述控制目標的重要概念而加以利用。文獻提出系統被控曲線軌跡形狀與參考軌跡曲線形狀合同的控制問題,結合相對曲率概念與曲線論基本定理,提出了一類雙輸入非線性系統二維平面形狀合同控制方法;文獻基于微分幾何平面曲線與空間曲線理論,提出了混沌系統形狀同步的概念,利用曲率構造相應的控制器,使驅動系統狀態軌跡與響應系統狀態軌跡的形狀完全相同;文獻針對一類具有不確定運動學和動力學特性的多機器人系統形狀控制問題,提出了一種有效的自適應控制方法。然而,文獻和主要考慮多機器人群隊列形狀控制,并未考慮系統狀態軌跡形狀控制;文獻提出的形狀同步控制均在假設曲線是正則的前提下,通過利用曲率構造控制器實現形狀同步,該方法并不適合于具有非正則狀態軌跡曲線的情形。從控制理論的角度看,上述文獻對形狀同步、形狀合同等控制問題的研究均可聚焦于形狀跟蹤問題。事實上,形狀不僅可通過弧長和曲率描述,還可通過剛體運動(旋轉、平移)加以描述。因此,基于剛體運動考慮其它類型的形狀漸近跟蹤控制器的設計方法也具有理論和實踐意義,但目前對該問題的研究甚少。
基于此,針對一類二維線性系統,本文利用剛體運動提出形狀漸近跟蹤的概念,結合模型參考自適應控制方法及LYapunov穩定性理論,為被控系統設計形狀漸近跟蹤控制器,以實現被控系統狀態軌跡形狀與參考系統狀態軌跡形狀的漸近跟蹤。本文提出的形狀漸近跟蹤控制器設計是基于一組模型匹配條件,這組模型匹配條件可視為傳統模型跟隨問題中模型匹配條件的擴展。本文提出的形狀漸近跟蹤可視為通常系統狀態漸近跟蹤問題的一般化。
本文首先描述被控系統與參考系統定義、形狀漸近跟蹤定義并提出假設;然后,結合Lyapunov穩定性理論進行形狀漸近跟蹤控制器設計和系統穩定性分析,進而得到形狀漸近跟蹤控制器及兩個參數自適應律;最后,通過仿真例子驗證形狀漸近跟蹤控制器有效性。
1 系統描述
在該條件下,通過求解方程(8)可得到K*和F*。
(2)若已知矩陣K*和F*,則式(8)可視為關于vec(MT)的線性方程,因而其有解的充要條件為:
在該條件下,通過求解方程(8)可得到滿足MMT=I的矩陣M。
通過式(6)事先給定的m維向量H和求解得到的矩陣M,使式(6)滿足有解的充要條件rank(AMT)=rank(AMT,BH),進而通過式(6)可求得二維向量N;當矩陣A可逆時,N=MA-1BH。
式(4)-式(6)為通常模型參考自適應控制設計中模型匹配條件(Erzberger Condition)的一般化,當M和N分別為單位矩陣和零向量時,即為常見模型匹配條件。
2 控制設計
本文控制目標是為二維線性系統設計形狀漸近跟蹤控制器,實現其與參考系統的形狀漸近跟蹤。為實現該控制目標,提出如式(11)所示的形狀漸近跟蹤控制器。
定理1:考慮二維線性系統與參考系統。若假設1成立,且參考系統所有信號均有界,則在形狀漸近跟蹤控制器(11)和自適應律(12)、(13)的作用下,二維線性系統與參考系統形狀漸近跟蹤。
證明:考慮正定函數,如式(16)所示。
針對正定函數(16)關于時間求導,可得:
3 數值仿真
為驗證本文方法有效性,利用Matlab軟件進行仿真實驗。矩陣A、Am、B、Bm與滿足假設1的正交矩陣M、控制器參數向量H由Matlab程序隨機產生。選取參考系統輸入um=[sint COSt]T,然后根據前文所述的第一種求解方法,按如下步驟求解K*和F*。
(1)根據方法一中有解的充要條件判斷是否有解,若無解則再次產生隨機矩陣,直到滿足有解條件為止,進而得到相應矩陣。
(2)求解式(8)中的矩陣方程,進而得到相應的K*和F*。
仿真結果如圖1-圖5所示。
從圖l和圖2可看出,雖然被控系統狀態軌跡與參考系統狀態軌跡位置不同,但其形狀是漸近相同的,這意味著被控系統狀態軌跡可通過一個合適的剛體運動后與參考系統狀態軌跡漸近重合,即達到了形狀漸近跟蹤。圖3-圖5分別說明了控制輸入及自適應律均有界。上述仿真結果表明,本文提出的形狀漸近跟蹤控制器可有效實現被控系統與參考系統的狀態軌跡形狀漸近跟蹤。
4 結語
研究結果表明,在一組合適的模型匹配條件下,形狀漸近跟蹤控制器可有效實現系統狀態軌跡形狀與參考系統狀態軌跡的形狀漸近跟蹤。雖然這些結論是基于二維線性系統得出的,但從本文理論分析可以看出,該方法也可擴展為一般維數的線性系統,而且相應模型匹配條件和矩陣求解方法也可進行擴展。現有文獻的控制設計方法并不適用于線性系統形狀漸進跟蹤控制問題,因此尋找合適的控制設計方法將是下一個研究內容。

