面向業務需求的航空白組網連通性研究

劉巖松 鄭欣 王金濤 龍巖

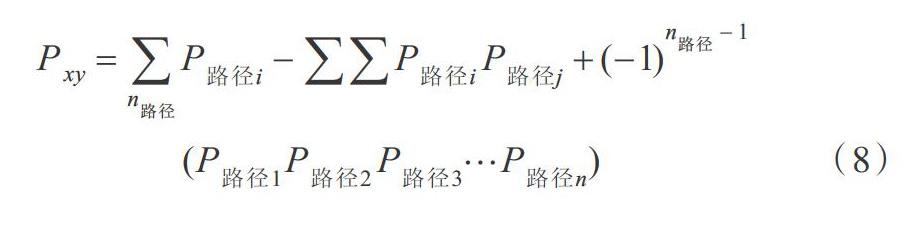
摘要：為滿足不同業務需求，保障業務實時性與穩定性，針對多種業務不同的鏈路連通性，提出適合不同業務的鏈路選擇方法。基于航空自組網近似模型，首先提出一種節點到基站的連通概率算法，其次根據飛機非勻速運動特點，運用Gauss-Markov移動模型，求出航空自組網連通時間，同時建立相應場景并進行仿真。結果表明，不同業務可根據程序計算結果選擇所需鏈路。

關鍵詞：鏈路;航空自組網;連通概率;連通時間

DOI：10.11907/rjdk.192222 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP393文獻標識碼：A 文章編號：1672-7800（2020）006-0240-04

0 引言

航空自組網（AeronauticalAd Hoc Networks，AANET）的出現推進了民航通信系統發展，它既可提供空中緊急救援、航行管理，還可提供機上娛樂、語音通信、因特網接人等服務。航空緊急救援是目前最有效的應急救援。德國空中救援組織要求空中緊急救援響應時間在8min之內，在過去的30年里，該組織已完成十萬多次空中急救任務，有近90萬人獲得急救，其中10多萬人因得到空中快速搶救得以生還，不過仍有近萬人因空中救援響應不及時而喪生。選擇較高連通概率鏈路可縮小救援響應時間，從而提高飛行活動安全性和可靠性。除了航空緊急救援，機艙內娛樂業務和語音通信等服務也依賴于飛機鏈路穩定性，自2013年來，中國國際航空實現運行第二代機上無線網絡系統，該系統擁有5個高性能處理器，存儲容量達到1T，每個AP可為50-70位旅客提供更豐富的娛樂內容。但機上娛樂等高帶寬業務需消耗少則幾十兆多則上千兆流量，航空白組網連通時間較長。所以不同業務選擇合適的鏈路尤為重要。

許多學者圍繞航空自組網連通性進行了研究。文獻[5]提出一種甚高頻航空自組網的解決方案，解決了飛行器之間不能直接通信、難以接人Internet等問題;文獻[6]提出一維航線連通概率公式以解決固定航線航空自組網連通性問題;文獻[7]提出交叉航線連通問題解決方法。但現有研究均存在理論與實際結合不緊密、研究場景只針對一維航線場景、節點沒有固定的運動軌跡等問題。

針對以上問題，本文首先建立航空自組網空中航線模型與空地航線模型，提出節點到基站連通概率計算方法;然后結合飛機非勻速運動的特點，基于Gauss-Markov移動模型，求出航空自組網連通時間，結合不同業務需求，建立相應場景進行仿真實驗。結果表明，不同業務可選擇合適的鏈路，保證相關業務穩定地完成。

1 模型建立

假設兩架飛機之間通訊半徑為R，即飛機節點之間必須小于或等于R才可連通，飛機數量服從泊松分布。

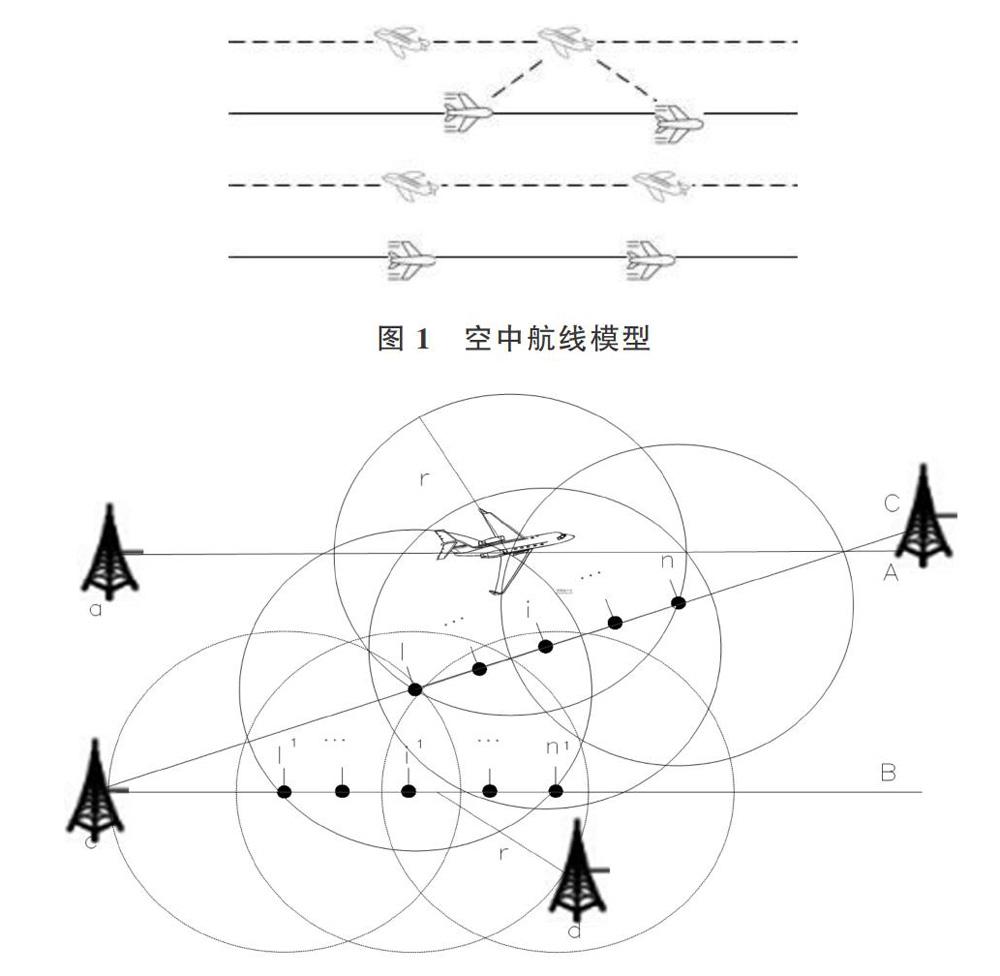
（1）模型1（空中航線模型）。空中航線模型大多采用雙向航線模型，如圖1所示。航線高度根據飛機飛行方向分成奇偶高度層，相鄰兩層的飛機飛行方向相反，且飛機之間相互獨立。

（2）模型2（空地航線模型）。空地航線模型表示為飛機與地面基站的通信模型，如圖2所示。圖中場景共有3條航線分別為A、B和C。地面有4個通訊基站，分別為a、b、c、d。飛機經過多跳直接或間接接人地基站，例如航線A上的飛機通過節點1跳到航線C，再通過節點1通信范圍內航線上的節點，最終接人地面基站d。

2 連通概率計算

基于航空自組網模型，計算節點到地面基站的連通概率，具體計算流程如圖3所示。本部分以圖2為例，詳細說明連通概率具體算法。

2.1 初始概率

航線A上的飛機節點跳到其通信范圍內的航段H_1n上等同于其通訊范圍內至少有一架飛機的概率，而任意一條航線飛機數量服從泊松分布，以坐標為（x，Y）的飛機節點為開始節點，計算其跳到通信范圍內航段H_1n的概率，記為P_初始，如式（1）所示。

其中，λ_b是航線B上的飛機密度，n是飛機總數。

2.2最后一跳概率

2.3 跳躍概率

如果航段h_1n.最后在地基站的通信范圍內，則可直接計算最后一條概率;否則，分別計算航段h_1n。上n個點的坐標概率，記為跳躍概率P_跳躍，如公式（3）-（5）所示。

2.4 任意兩個節點連通概率

通過上述步驟得到節點（x，y）到地基站的所有路徑概率，如公式（7）所示。

記路徑i=（1，2…n），存在事件i，事件i發生的概率為P_路徑。至少有一個事件發生的概率即為節點到地面基站的連通概率，使用概率論加法公式，如式（8）所示。

3 連通時間計算

3.1 鏈路連通時間

在航空自組網中，群組移動是隨機的，且會影響前后節點速度。Gauss-Markov模型相比于其它群組，移動模型具有前后運動相關性，每隔一段時間即根據當前速度改變一次，第n次運動由第n-1次運動速度值和一個隨機變量決定，如式（9）所示。

其中，v_n表示節點在第n個步驟的速度值，a表示趨近于無窮大時的平均值v_n-1，其符合高斯分布隨機變量∝ ∈[0，1]，用來調節運動隨機性，根據相應的速度公式可以求出連通時間。假設其中一個節點速度為v₁，另一個速度值為v₂，兩個節點距離為D，因為只有當飛機之間的距離小于通信距離才會實現全聯通，假設兩個飛機之間的通信距離為R，則有限制條件D

當兩個飛機位于單條航線上，兩個飛機方向相同，距離為：

3.2 信息所需連通時間

信息大小約為C，鏈路傳遞速率為s₁，根據公式（14）可求得信息所需連通時間。

鏈路連通時間與信息連通時間不同，通常鏈路連通時間大于信息所需時間，才可順利傳輸信息。

4 仿真環境

以航空白組網的空中航線模型和空地航線模型為背景，結合不同業務需求，在MATLAB平臺上構建仿真場景。仿真包括兩組實驗：場景l以空地航線模型為背景，模擬飛機出現故障的緊急情況;場景2以空中航線為背景，模擬鄰近飛機信息傳遞情況。

4.1 仿真場景1

假設一架A320飛機有一名因消化道大出血導致失血性休克的患者，機組人員急需與地面基站取得聯系，此時飛行場景大小為1000km x 1000km，航線數目為6，飛機通信半徑300km，航線長度800km，飛機間安全距離40km，基站坐標（450kin，250km）。航線參數信息如表1所示。

使用本文提出的多航線航空自組網連通概率計算方法，得出該場景下最大概率鏈路，如圖4所示。

如圖4所示，以黑色三角為飛機起始點，根據泊松分布計算第一跳概率，以此為圓心，通信范圍為半徑，得到與周圍航線相交的離散點。分別計算這些離散點轉移概率，其中點5連通概率最大，以此作為下一跳，最后直接接人地面基站，該路徑為最大概率鏈路。各鏈路概率值如表2所示。

根據概率值得出不同鏈路連通概率與時間的關系，如圖5所示。其中橫坐標為連通時間，單位為s，縱坐標為連通概率。

由圖5可以看出，A320發生緊急情況時，為實現快速與地面取得聯系，應在周圍5條可連通的鏈路中，選擇最大概率的鏈路。

4.2 場景2

假設飛機1上乘客A正在通過航空自組網給另一架飛機5上的乘客B傳送視頻。視頻大小約50M，飛行場景大小為600km x 800km，航線數目3，飛機相互之間距離均在通訊半徑內。分別根據表3的飛機參數和表4的鏈路參數，求出鏈路連通時間和信息連通時間，再進行對比，如表5所示。

通過表5可知，這3個鏈路中飛機鏈路1-2-5和飛機鏈路1-3-5的帶寬較大且連通時間大于信息傳遞時間，可以實現信息傳遞。其中飛機鏈路1-2-5本身連通時間較長，穩定性更強，所以選擇飛機鏈路1-2-5。

綜合以上分析可得出該場景下飛機最長連通時間路徑，如圖6所示。

飛機l向飛機5傳送視頻時，因流量較大，需較長的連通時間鏈路，在周圍3條鏈路中，應選擇鏈路1-2-5。

5 結語

本文針對不同業務有不同鏈路連通性的需求，結合航空自組網空地模型和空中航線模型，提出了節點到基站連通概率算法，并應用Gauss-Markov移動模型，求出航空自組網飛機節點間的連通時間。不同業務根據計算結果選擇對應鏈路可保證業務高效穩定地完成。本文對于業務類型涉獵有限，因此下一步將使航空白組網與更多類型業務結合，為航空白組網連通性研究提供重要參考。