帶預載的彈簧柔性體在減振支柱設計中的應用

盧蕾蕾

摘 要：本文根據麥弗遜式懸架減振支柱的結構，在動力學仿真軟件ADAMS中創建麥弗遜式前懸架動力學模型后，進行仿真用以分析彈簧對減振支柱的側向力補償。使用一種帶預載的柔性體來模擬預壓縮的懸架彈簧，通過與ADAMS自帶的力向量彈簧模型進行對比，可知前者能夠更準確地模擬“C”形彈簧的受力軸線隨輪跳變化的情況。

關鍵詞：預載;彈簧;柔性體

1 前言

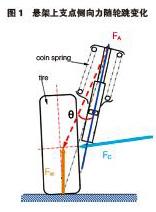
麥弗遜式前懸架具有結構簡單，占用空間小的特點，因此在發動機前置前驅轎車上得到廣泛的應用。其中的減振支柱總成除了具有緩沖、限位和減振的作用外，還在懸架機構運動中承擔著導向和支撐的作用[1]，使得減振支柱總成的設計尤為重要。要求減振支柱所受的側向力盡可能的小，以減少活塞桿與減震套筒間的摩擦，提高零件的使用壽命。因此在設計其彈簧減振器總成時，通常會將彈簧受力軸線相對減振器軸線有一個向外的偏置角，以抵消支柱受到的側向力，如圖1所示。當彈簧力FA，控制臂球頭力FC，地面反作用力FW交于一點時，減振器上支撐點所受側向力為零。受到空間限制，彈簧下點無法向外偏移過大，同時懸架運動學的限制，彈簧下安裝點相對于減振器上支撐點的運動軌跡為空間弧線，也就是說彈簧并非是沿著直線壓縮和伸長，因此彈簧軸線的設計需要考慮車輪跳動時的受力情形。

2 力向量彈簧

在彈簧減震支柱的設計初期可在ADAMS軟件中仿真其在工作中的受力狀態。彈簧在ADAMS中被簡化成一個因變形而產生力的彈性元件，通過一個連接彈簧上下硬點的力向量表達，力向量的大小則通過公式（1）計算得到[2]：

其中，Fs為彈簧力，K為彈簧剛度，D（i，j）為彈簧上下硬點之間的距離，隨著車輪跳動而變化，ls為彈簧原長。通常情況下由于車身自身的重量作用，彈簧具有一定的預壓縮量，其產生向上的支撐力Fs支撐車身，向下的壓力Fs保持車輪在地面上滾動，故D（i，j）的初始長度小于ls。

在設計彈簧減振支柱總成時，需要分析減振器上支撐點的受力狀況。如果彈簧設計合理，將會抵消大部分的側向力，此時減振支柱上支撐點所受側向力減小，只在軸向承受大部分載荷，故具有良好的耐久壽命。麥弗遜懸架中減振器的上支撐是由金屬支架，軸承（提供車輪轉向時所需的旋轉自由度）和橡膠（起到過濾小幅振動的作用）等組成。仿真時用襯套的六個方向的剛度來表示，通過在后處理結果中查看襯套承受側向力的大小可以確定彈簧力是否對側向力有足夠的補償。

對麥弗遜懸架進行平行輪跳仿真，考察減振器上支撐襯套所受側向力隨輪跳變化。通過設計彈簧的偏置角，在輪跳為零時可以使上支撐點所受側向力為零。但此時彈簧力向量較大，不滿足彈簧布置所需空間的要求。同時，隨著車輪上跳上支撐點所受的側向力也逐漸增大，彈簧的側向力補償并未達到最優。因此在設計彈簧時，為了盡可能多地補償側向力，一般會采用彈簧軸線呈“C”形的“C”形彈簧以獲得變化的彈簧偏移角，同時避免使彈簧下安裝盤向外偏移過多，以節省側向空間。

3 柔性體彈簧

設計中采用“C”形彈簧具有較好的效果，卻無法在ADAMS中直接使用其自帶的彈簧力向量去模擬“C”形彈簧，ADAMS軟件算法將彈簧定義為一個力向量，方向沿“C”形彈簧上點的切線方向，卻不能表示沿著“C”形彈簧軸線的力。為了更好地模擬沿彈簧力軸線變化的彈簧力，根據彈簧的實際形狀，創建彈簧的柔性體模型代替力向量。

多體動力學軟件一般采用模態綜合法生成柔性體的模態中性文件，在計算時通過一個包含柔性體模態信息的矩陣文件描述柔性體，利用模態振型的線性疊加來表示柔性體的變形。對于施加了預載荷的柔性體模型，其矩陣文件還包含預載荷矩陣，通過一組數列描述分解在各個模態振型上的預載。在ADAMS中，柔性體的運動方程見公式（2）：

其中，，，為柔性體廣義坐標及時間導數;M為柔性體質量矩陣;為柔性體質量矩陣的時間導數;為柔性體質量矩陣對廣義坐標的偏導數，是一個（N+6）×（N+6）×（N+6）的張量，其中N是模態階數;K為廣義剛度矩陣;fg為廣義重力;D為模態阻尼矩陣;為代數約束方程;λ為約束方程的拉格朗日乘子;Q為施加的廣義力[3]。

前文提到彈簧安裝在懸架上時存在預壓縮量，因此在生成彈簧柔性體時分兩步：第一步，先對自由狀態下的彈簧數模進行有限元前處理后進行固定邊界的模態分析，生成模態中性文件;第二步，編制預載文件，重新計算生成帶預載的模態中性文件。彈簧柔性體所受的預載必須為一對大小相等，方向相反的內力，將其從自由長度壓縮至安裝長度。此彈簧柔性體在導入ADAMS后，若在無約束狀態下會從安裝長度自動回彈至自由長度，在約束狀態下則會對約束物體產生反作用力，這與公式（1）描述的力向量模型一致，也與彈簧在實際裝配時的狀態吻合。

4 結果對比

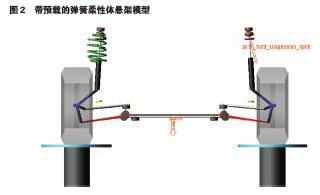
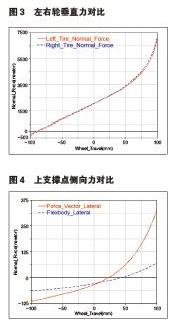
為便于對比，對一款上市車型的麥弗遜式前懸架創建動力學模型，右側懸架使用帶預載的柔性體彈簧，左側懸架使用軟件自帶的單個力向量表示彈簧，創建模型如圖2所示。為了使獨立懸架的左右兩側互不影響，對懸架進行平行輪跳仿真，對比左右兩側懸架的輪胎垂向力以及減振器上支撐點的側向力。由圖3可以看出，左右兩側懸架所受的垂向力隨輪跳的變化曲線基本相同，左右兩側懸架在設計位置（輪胎上跳量為零時）所受地面的反作用力均為2060N，說明柔性體彈簧的預壓縮量產生的反作用力與實際一致，驗證了柔性體彈簧模型的準確性。又可以從圖4中看出，右側懸架在車輪跳動時，其減震支柱上支撐點承受的側向力要小于左側承受的側向力，且力隨輪跳的變化曲線更平緩。說明彈簧與減振器夾角的設計可以有效的抵消側向力，使得減振器上支撐點受到的側向力小于設計要求的70N，避免減振器受到側向力后產生磨損。可見，采用柔性體的彈簧模型有效地模擬“C”形彈簧的受力軸線，符合彈簧受力隨著輪跳而變化的設計要求，從而驗證了產品設計的合理性。

5 結論

在對產品進行仿真驗證時，分析各個零件的設計意圖是創建模型的關鍵，以此為前提采用合適的方法建模才能保證模型正確地模擬產品功能。麥弗遜懸架的減振支柱的受力分析關系到整個支柱總成的使用性能和壽命。在計算減振支柱的側向力時，應考慮到彈簧受力的方向是隨著車輪跳動位置而變化的。本文根據模態綜合法創建彈簧柔性體，并施加預載后導入ADAMS軟件進行建模仿真，模擬彈簧在懸架跳動時的變形過程。通過與ADAMS自帶的彈簧模型對比，驗證了模型的可行性和準確性。這種方法在帶有預載荷的模型中都可以使用，為動力學建模提供了一種新的思路，拓寬了剛柔耦合模型在實際工程中的應用范圍。

參考文獻：

[1]姜鵬，汽車懸架系統的仿真分析與參數優化設計[D].浙江大學，浙江：2006.8-9.

[2]Using ADAMS/Car.2013.

[3]Using ADAMS/Flex.2013.From The Automotive Chassis： ?Engineering Principles，J. Reimpell & H. Stoll， SAE 1996.