基于凸優化的共形陣波束優化方法研究

王曉慶，梁浩前，王大宇，陳衛東

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

共形陣列在進行波束形成[1-5]時，如果不采用一定的波束旁瓣控制手段，其旁瓣影響往往都會很大。因此，低旁瓣波束形成設計是共形陣列抑制旁瓣干擾、提高目標信號檢測概率的重要手段之一。 Taylor[6]等人提出了針對均勻線陣的旁瓣控制方法，Hyneman和Johnson[7]研究了波束函數零點移動的策略來控制波束旁瓣；Dolph[8-9]提出了針對均勻線陣的旁瓣控制權值；Stern[10]提出了水下陣列可以使用Taylor的結果。

1990年，Olen和Compton[11]研究了波束旁瓣控制的數值綜合法，該方法通過優化迭代，給出了針對給定陣列及主瓣寬度和旁瓣級情況下的最佳權值，文獻[12-13]都是在此基礎上開展的研究，解決了存在陣列誤差時的旁瓣控制方法。文獻[14]研究了寬帶模型下的波束旁瓣優化設計方法。文獻[15]基于數值綜合法提出了多線性約束的陣列天線方向圖旁瓣抑制方法，有效解決了在有限快拍下常規波束形成器旁瓣過高的問題。

但是，Dolph提出的方法無法運用于共形陣列，在處理非均勻或非共線的陣列時性能惡化。數值綜合法在迭代計算過程中容易發散，迭代步長過大會使算法性能穩定性變差。因此，仍需要研究適用于共形陣列且性能穩定的旁瓣控制方法。

隨著科技的發展和進步，很多學者開始使用凸優化理論來實現對陣列的波束優化控制，其中運算簡單、結果精確的二階錐規劃方法[16]得到了廣泛應用。

本文基于凸優化技術，提出了2種波束旁瓣控制方法，可以解決水下共形陣的旁瓣級高的問題，一種是旁瓣最低主瓣最小加權CBF法，另一種是給定旁瓣級的高增益加權CBF法。這2種方法均對加權向量范數進行約束，使用內點法[16]迭代，從而抑制共形陣波束形成的高旁瓣。計算機仿真表明，針對水下共形陣列旁瓣控制問題，2種方法均具有良好的性能。該方法能夠推廣到對空間無線電陣列信號處理應用中，具有非常好的實用前景。

1 共形陣常規波束形成器

本文設計的共形陣列為空間陣列，假設空間共形布設的陣列，遠場P點處有一水聲信號，如圖1所示。

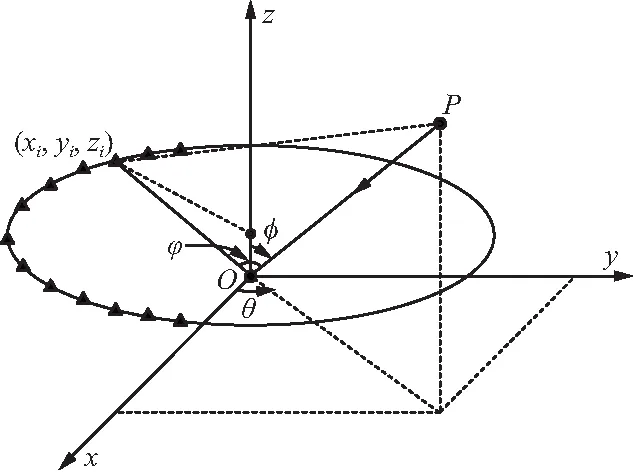
圖1 水下共形陣列接收遠場信號示意Fig.1 Diagram of underwater conformal array receiving far field signal

其中，N為陣元個數，各水聽器的位置三維坐標為ri=[xiyizi]T，(·)T表示轉置；θ，φ為聲源的方位角和俯仰角，則該方向的單位向量為：

u=[sinφcosθsinφsinθcosφ]T，

則基陣對從(θ，φ)方向入射到基陣的窄帶信號的響應向量為：

式中，c為聲速；f為水聲信號頻率；di(θ，φ)是第i個陣元對(θ，φ)方向的響應幅度大小。

則，對(θ，φ)方向，陣列的波束響應可以表示為：

p(θ，φ)=dH(θ，φ)w，

式中，(·)H為向量的共軛轉置；w為陣列的加權向量。令φ=90°，本文僅討論水平方向的波束形成。則基陣的陣列流形矩陣可以表示成(省略φ)：

D(Θ)=[d(θ1)d(θ2) …d(θM)]，θ1，θ2，…，θM∈Θ，

式中，θ1，θ2，…，θM為離散化的方位角，往往覆蓋0°～360°。基陣的水平方位波束圖表示為：

對于均勻線陣，其陣元可以認為是各向同性的，通過陣元位置可以很方便地解算其陣列流行。水下共形基陣陣元安裝在一個球形支撐架上，支撐架對信號的遮擋和散射導致了各陣元對各方向信號的響應大小不同。如果不考慮支撐架的影響，其數學模型的建立是基于共形陣陣元完全相同，陣元相互間無影響的假設，陣元指向性為全向，這種模型稱之為共形陣的透聲模型，可以很方便地計算得到其陣列流形。

但實際上共形基陣的指向性受后障板的影響很大，共形陣支撐架對陣元的影響是不可忽視的。一個全向接收的水聽器放在支撐面上后，受后障板影響出現了指向性[17]。障板模型下共形陣陣元指向性如圖2所示。試驗測得其指向性平均值。

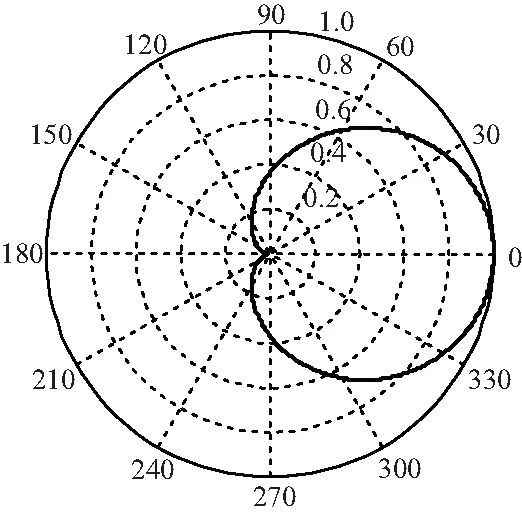
圖2 障板模型下共形陣陣元指向性Fig.2 Directivity map of conformal array elements with the baffleplate

則：

式中，φ為信號入射方向與陣元聲接收主軸的夾角，如圖1所示。

如果認為共形陣列上的陣元均具有上述指向性特點，并且一致性非常好。則可以提出一種全新的共形陣列接收模型——障板模型。對于障板模型，可以仿真得到其理想陣列流形。如果未加強調，本文所做的仿真均在障板模型下完成。

2 基于凸優化的波束旁瓣控制

本文使用Sturm公司開發的Matlab工具箱SeDuMi[18]來求解二階錐規劃和低旁瓣約束條件下的凸優化問題。其迭代運算量小、優化精確度高，并且可以自動判定求解的欠定方程是否有解。在SeDuMi中，標準的凸優化問題可以表示為：

maxbTysubject toc-ATy∈S，

式中，A為一個矩陣；y為期望向量；b，c為任意向量；S為一個對稱錐集合。A，b，c的維數必須匹配，且都可以為復數。則q維二階錐表示為：

實數域的三維(q=3)二階錐幾何意義示意如圖3所示。

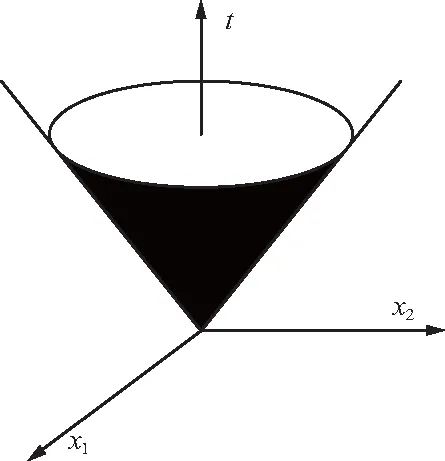
圖3 二階錐幾何意義示意Fig.3 3D second order cone of real number field

由圖3可以看出，在該錐內，二階錐優化的幾何意義是尋找滿足目標函數最大化的最優點。

如果為等式方程，則意味著零錐，零錐定義如下：

{0}={x∈C|x=0}，

式中，C為復數集。假設約束問題可以表示為：maxbTysubject toc-ATy∈{0}q1×Qq2的形式，則Matlab工具箱SeDuMi可求出其數字解。上述約束包含q1個等式，并且q2個元素位于二階錐內。

2.1 最低旁瓣級加權

最低旁瓣級加權CBF的約束準則為使波束掃描方向的幅度加權值為1，在對加權向量進行范數約束[19]的條件下，控制最大旁瓣值最小化。則上述公式可表示為：

式中，ξ為加權向量的范數最大；θs為波束掃描方向；Δ為波束主瓣寬度的一半。令θi，i=1，2，…，I，為旁瓣部分的離散化的I個方向(可以讓這I個方位均分旁瓣方位)，并且增加一個非負實變量y1，則上式可以表示成：

令y=[y1wT]T，b=[-10T]T，使y1=-bTy。其中0是N×1的零向量，對于式中的約束可以寫成：

AT=[A1A2…A1+IA2+I]T，

則低旁瓣波束形成可以表示為標準的二階錐約束形式：

上述方程，可使用Matlab工具箱SeDuMi進行求解，得到所需的最低旁瓣級加權向量w。

2.2 給定旁瓣級的高增益加權

給定旁瓣級的高增益CBF加權的約束準則如下：

式中，Rn為噪聲協方差矩陣。對Rn進行Cholesky分解，即：

Rn=UHU，

得到：

wHRnw=(Uw)H(Uw)=‖Uw‖2。

對權向量的范數進行約束條件下，給定旁瓣級的高增益CBF約束準則可再加入旁瓣級控制。令y1為非負實變量，上述約束修改為：

式中，形成波束的旁瓣級由δi決定，但旁瓣等級在不同方向上不一定相同。

令y=[y1wT]T，b=[-10T]T，使y1=-bTy。其中0是N×1的零向量，對于上式中的約束可以寫成：

則旁瓣控制高增益波束形成可以表示為標準的二階錐約束形式：

將d(θs)，d(θi)(i=1，2，…，I)代如上述各式中，則上述方程可使用Matlab工具箱SeDuMi進行求解，得到所需的最低旁瓣級加權向量。

3 共形陣常規波束仿真

依據文獻[20]建立72元四排環帶型共形陣，按20 kHz，陣間距37.5 mm布陣。外側曲面為半球形[21-22]，四排曲線陣在球面上排列，每排曲線有18個陣元，陣元間距為37.5 mm，當水中聲速為1 500 m/s，頻率為20 kHz時，λ/2為37.5 mm。陣元間距等于半波長，滿足空間采樣定理。建立的72元四排環帶型共形陣如圖4所示。

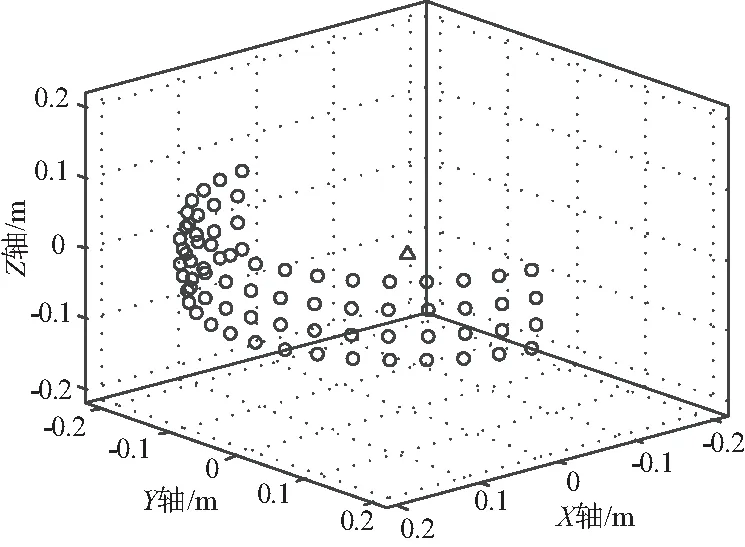
圖4 四排環帶型共形陣布陣(三維)Fig.4 Diagram of four-row ring belt conformal array (3D)

為了研究上述四排環帶型共形陣的常規波束特點，沿其水平方向進行常規波束形成。設水中聲速為1 500 m/s，頻率為20 kHz。為便于對比，選取0°，-30°，-60°共3個方向進行分析。陣元指向性使用文獻[20]中的帶障板的水聽器模型。

四排環帶型共形陣的頂視圖和前視圖如圖5所示。

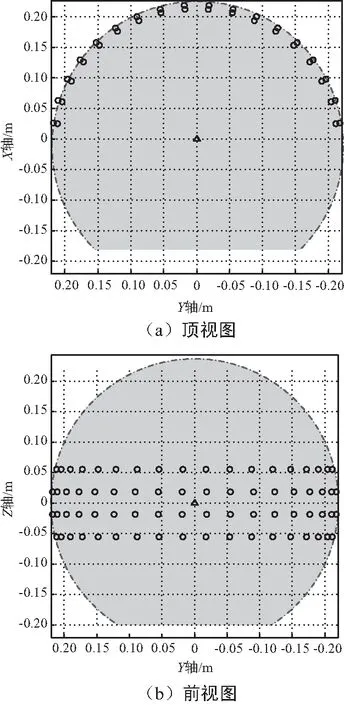
圖5 四排環帶型共形陣的頂視圖及前視圖Fig.5 Top and front views of four-row ring belt conformal array

四排環帶型共形陣的水平波束如圖6所示。

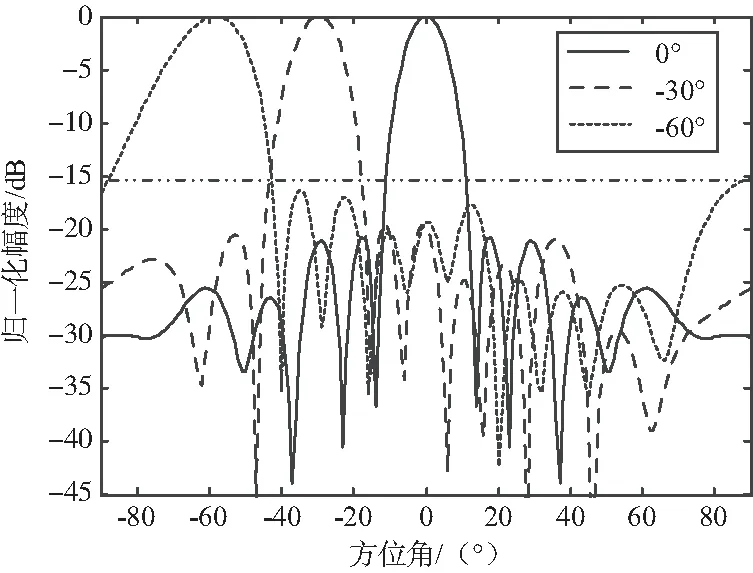
圖6 四排環帶型共形陣的水平波束Fig.6 Horizontal beam pattern of four-row ring belt conformal array

由圖6可以看出，四排環帶型共形陣的水平波束旁瓣級較高，尤其在偏離正橫方向-60°的掃描扇面附近。在帶障板的模型下，旁瓣級仍然達到了-15 dB。

4 共形陣波束優化仿真

假設信號頻率為20 kHz，使用本文方法對建立的72元四排環帶型共形陣常規波束進行優化設計。通過與常規波束以及其他波束優化方法的對比，驗證了本文所提波束優化方法的有效性。

4.1 最低旁瓣級加權

仿真中使用本文提出的旁瓣最低主瓣最小波束優化方法(簡稱最低旁瓣級加權算法)同傳統的Dolph算法進行對比。波束指向-60°，分別采用基于二階錐規劃的最低旁瓣優化算法和Dolph算法波束形成，得到旁瓣級為-25 dB的波束圖，比較2種算法的權向量如圖7所示。

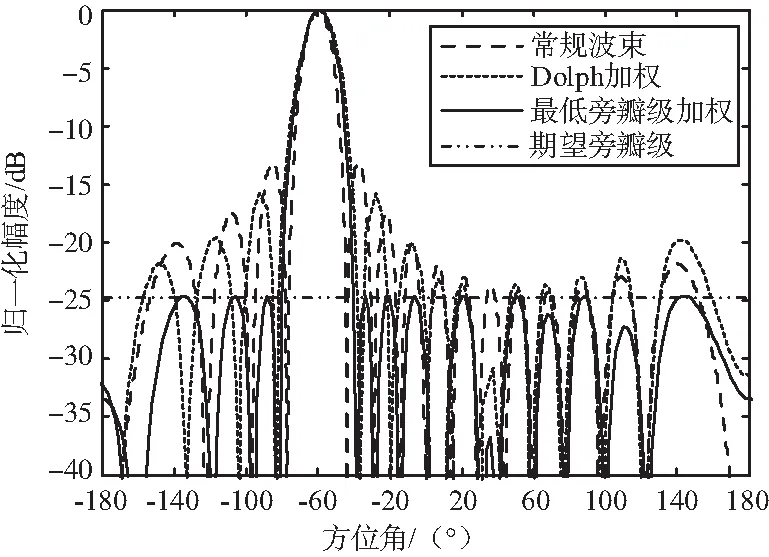
圖7 最低旁瓣級加權對比仿真Fig.7 Contrast simulation of minimized sidelobe level beamforming

由圖7可以看出，應用于共形陣波束旁瓣控制問題時，Dolph加權算法性能惡化，而基于二階錐規劃的最低旁瓣級加權算法能有效地將旁瓣約束至-25 dB的等級。

不同主瓣寬度下最低旁瓣級加權仿真如圖8所示。

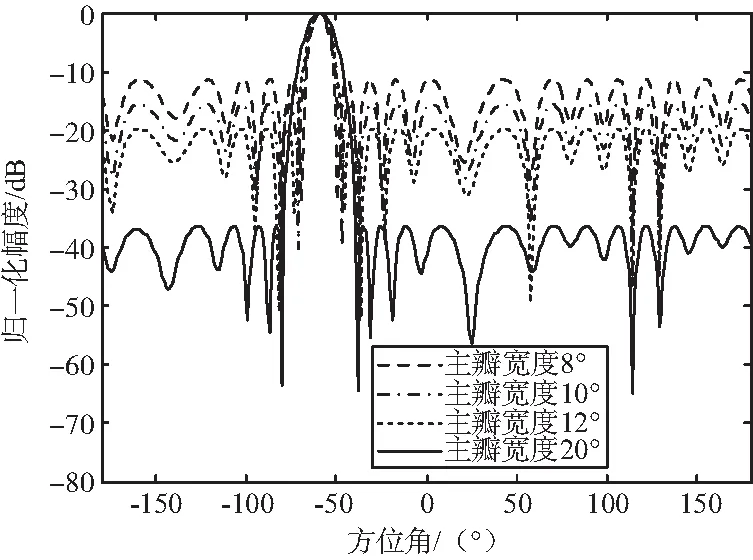
圖8 不同主瓣寬度下最低旁瓣級加權仿真Fig.8 Beamforming simulation with diffrent mainlobe widths

由圖8可以看出，在主瓣寬度一定的情況下，基于二階錐規劃的最低旁瓣級加權算法始終可以得到最低的旁瓣等級。

4.2 給定旁瓣級的高增益加權

仿真中分別采用Dolph算法、文獻[11]中使用的數值綜合法以及本文提出的給定旁瓣級的高增益加權算法進行波束優化，并比較這幾種算法的結果，波束指向為0°，期望優化的波束旁瓣級為-30 dB。比較上述3種方法和常規波束形成，給定旁瓣級的高增益加權對比仿真1如圖9所示。

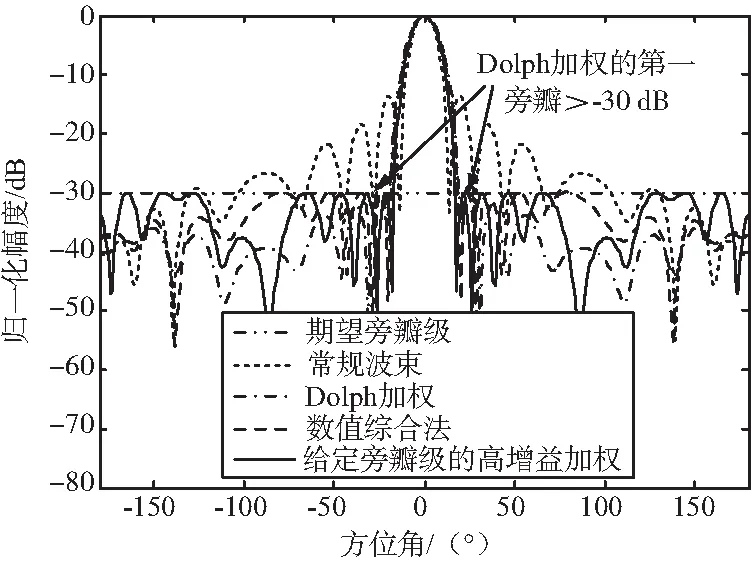
圖9 給定旁瓣級的高增益加權對比仿真1Fig.9 Contrast simulation 1 of maximized array gain sidelobe control beamforming

由圖9可以看出，Capon方法的旁瓣級仍然很高。數值綜合算法和本文提出的給定旁瓣級的高增益加權算法都將旁瓣控制到了期望的水平。

給定旁瓣級的高增益加權對比仿真1(局部放大)，如圖10所示。

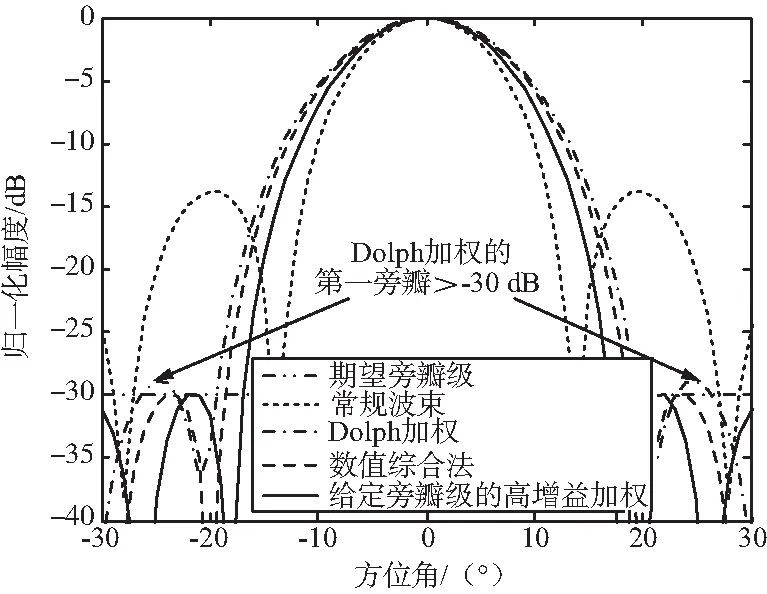
圖10 給定旁瓣級的高增益加權對比仿真1(局部放大)Fig.10 Contrast simulation 1 of maximized array gain sidelobe control beamforming (partial zoom-in)

通過圖10的局部放大圖發現，Dolph算法的第一旁瓣略高于期望的旁瓣等級，并且各個方向上的旁瓣水平高低不均勻。相比于數值綜合算法，本文提出的給定旁瓣級的高增益加權算法具有更集中的主瓣寬度。

將波束指向調整為-30°，繼續考察數值綜合算法和本文提出方法的穩定性。給定旁瓣級的高增益加權對比仿真2，如圖11所示。

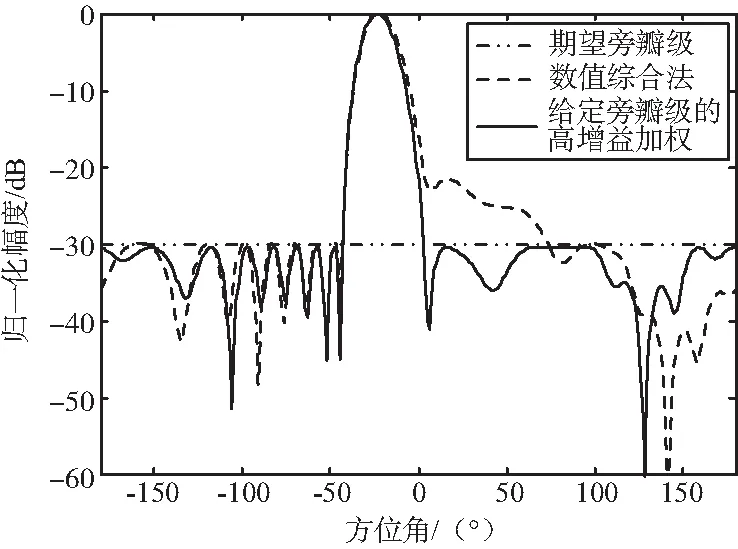
圖11 給定旁瓣級的高增益加權對比仿真2Fig.11 Contrast simulation 2 of maximized array gain sidelobe control beamforming

由圖11可以看出，數值綜合算法存在不收斂的問題，最終導致得到的波束圖發生畸變，使得數值綜合算法在穩定性上存在隱患。而本文提出的給定旁瓣級的高增益加權算法依然能夠獲得期望的旁瓣級控制，性能更加穩定。

將波束指向調整為60°，期望優化的波束旁瓣級為-40 dB，并且加入15%的陣元間距和各向同性誤差，繼續考察數值綜合算法和本文提出方法的旁瓣控制效果。給定旁瓣級的高增益加權對比仿真3，如圖12所示。

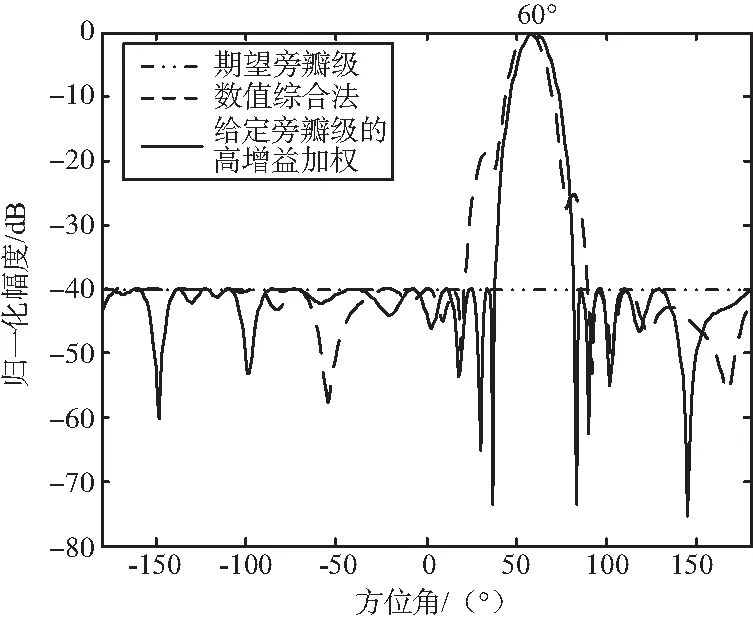
圖12 給定旁瓣級的高增益加權對比仿真3Fig.12 Contrast simulation 3 of maximized array gain sidelobe control beamforming

由圖12可以看出，數值綜合算法在共形陣列陣元間距和各向同性存在誤差的情況下主瓣指向出現偏差，旁瓣發生畸變，數值綜合算法失效，而本文提出的給定旁瓣級的高增益加權算法依然有效。可見，本文算法針對陣元間距和各向同性誤差具備一定的容錯能力。

5 結束語

本文基于凸優化技術，致力于解決水下共形陣列波束形成時出現的旁瓣電平高的問題，提出了2種適用于水下共形陣列的旁瓣約束優化波束形成算法，一種是旁瓣最低主瓣最小加權CBF法，另一種是給定旁瓣級的高增益加權CBF法。2種方法均對加權向量范數進行約束，使用內點法迭代，從而抑制共形陣波束形成的高旁瓣。前一種方法使波束掃描方向的幅度加權值為1，從而控制最大旁瓣值最小化；后一種方法在給定旁瓣級的高增益約束基礎上再加入旁瓣級控制。仿真結果表明，針對水下共形陣列旁瓣控制問題，2種方法均具有良好的性能。該方法適用于任意幾何形狀和陣元指向性的傳感器陣列，應用前景廣闊。