EGM2008重力場模型在高程異常擬合中的應用

柯生學

（中國電建集團西北勘測設計研究院有限公司，陜西 西安 710100）

0.引言

傳統水準測量精度高，可靠性強，但往往耗費大量人力物力，測量速度慢，且受天氣氣候約束[1-4]。GNSS測量能在布網控制點上獲得正高，但我國使用的是正常高系統（基于似大地水準面），為使測量結果能直接使用，必須計算高程異常值[5,6]。高程異常擬合需要獲得測區一定數量的控制點坐標、大地高、正常高，若使用重力場模型還需要獲得對應重力場模型計算的長波項，根據區域高程、高程異常值等條件選擇適合本區域的擬合模型[7-10]。傳統高程異常擬合模型受限于數學模型的特點，難以達到較高精度[11-13]。EGM2008 重力場模型作為美國發布的新一代重力場模型，可以精確計算待定點重力項高程異常，將之與移去-恢復法及常規數學模型結合，可以極大地提高高程異常擬合精度[14,15]。本文以西安某區域GNSS 水準數據為例，通過多項式擬合法、最小二乘配置擬合法、半參數模型結合移去-恢復討論小區域高程異常擬合的最優模型[16,17]。

1.高程異常擬合的理論與方法

高程異常擬合有多種理論，本文主要采用以下三類：多項式擬合法、最小二乘配置法、半參數模型。

1.1 多項式擬合法

多項式擬合法是通過選取一定的擬合系數數量來控制模型起伏的一種數學模型，最少選擇三個擬合系數，這時模型就是平面擬合模型。隨著選擇的擬合參數增加，模型起伏會有所變化，所需要的最少起算點也會隨之增加。一般選擇六參數多項式。擬合參數并非多多益善，因為擬合參數的增加會引起模型曲面的復雜起伏變化，有時反而會降低擬合精度。

多項式擬合模型可用式（1）表示：為高程異常；ε為殘差；ai為待擬合參數；B，L為大地經緯度。誤差方程式（2）為：

擬合系數矩陣

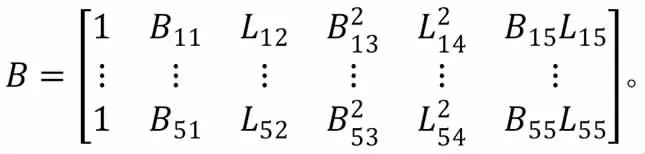
根據以上式可知多項式擬合至少需要六組已知點的高程異常及大地經緯度。將公共點數值帶入上式，可得待估擬合參數X 計算公式（3）為：

1.2 最小二乘配置法

最小二乘配置法是一種優化模型，需要基于某個基礎模型進行精度，一般優化六參數多項式。六參數多項式僅考慮到模型趨勢項影響，未考慮非趨勢項即隨機誤差的影響。最小二乘配置法將非趨勢項作為優化目標，通過計算提高模型擬合精度。

最小二乘配置法可用公式（4）表示：

式中，L為已知點高程異常值，X為函數模型部分待擬合參數，B為函數模型部分系數矩陣；S為觀測信號；Δ 為觀測信號噪聲。以S'表示未知點高程異常觀測信號，式（5）可表示為：

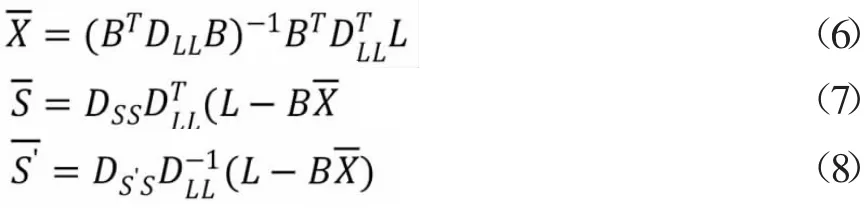
式中，DLL=DΔΔ+CDZZCT；未測點的最或然值見式（9）：

1.3 半參數模型

半參數模型可用式（10）表示：

式中，L為已知點高程異常；B，X為參數模型函數系數矩陣與待估參數；S為半參數分量；Δ 為誤差分量。誤差方程見式（11）：

式中，P為權陣（正定矩陣）；α 為在極化過程中平衡V與S的純量因子，稱平滑因子；R為給定的正則化矩陣。由式（10）構造極值函數，可解參數分量與非參數分量

式中，N=BTPB；M=P+αR-PBN-1BTP。

依據最小距離法選取平滑因子α，αD為曲線上的點到原點距離最小時對應的α，當Sn2(αD) +Vn2(αD)=min時，α取得最優值，非參分量最優值經平差計算獲得。利用式計算傾向參數Y，結合S計算出X，內插獲得待算點的高程異常值見式（15）：

2.高程異常擬合優化基于—EGM2008 的移去恢復

高程異常可分為以下幾個部分：由重力場模型確定的中長波部分ξG、由Stokes理論確定的重力異常殘余分量ξS、由地形改正得到的短波部分ξD。“移去-恢復”法的基本思想是：移去高程異常中的長波部分或者短波部分，然后將剩余部分結合擬合模型進行擬合計算，最后在待定點上恢復被移去的部分。由于缺少高分辨率的DTM數據，本文將短波部分與殘余分量合并作為殘差高程異常ξΔ=ξS+ξD。計算過程如下：

（1）根據GNSS 水準數據計算每點高程異常ξ'；

（2）將ξ'與以EGM2008 模型計算的中長波部分ξG相減，得殘差高程異常ξΔ；

（3）選擇擬合模型對ξΔ進行擬合，確定最優待定參數，建立殘差高程異常擬合模型；

（5）將外推所得ξΔ'恢復中長波部分,得該點高程異常擬合值

（6）對模型進行內外符合精度評定以及殘差計算。

3.算例

3.1 工程概況

本文所用數據來自西安某區域，南北長約55 km，東西寬約30 km，地面標高為+35.38m～+36.29 m。礦區共有3 個C 級GNSS 點、19 個D 級GNSS 點和24 個E級GNSS 點，總計46 個GNSS 點都進行了相應等級的水準聯測，礦區GNSS 點分布（如圖1 所示）。

由圖1 可知，已知點分布不均勻，因此以3 個C 級點做起算點，在礦區已有基礎上，新增10 個GNSS 點進行D 級GNSS 測量，大地高與正常高觀測結果（如表1 所示），由表可知所有點大地高變化不大，點位穩定可靠。

3.2 方案設計

根據測區概況，共設計六種計算方案，分別為：（1）六參數多項式；（2）六參數多項式+移去恢復；（3）最小二乘配置；（4）最小二乘配置+移去恢復；（5）半參數；（6）半參數+移去恢復。分別計算六種方案的擬合殘差與內外符合精度進行對比。

3.3 實例計算與精度分析

圖1 礦區已知點分布

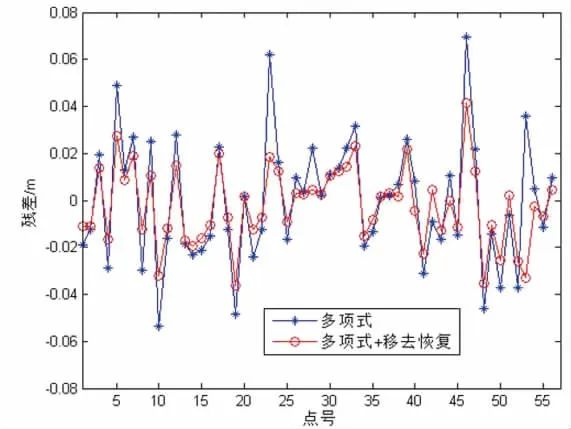
圖2 多項式殘差對比

表1 GNSS 點可靠性分析

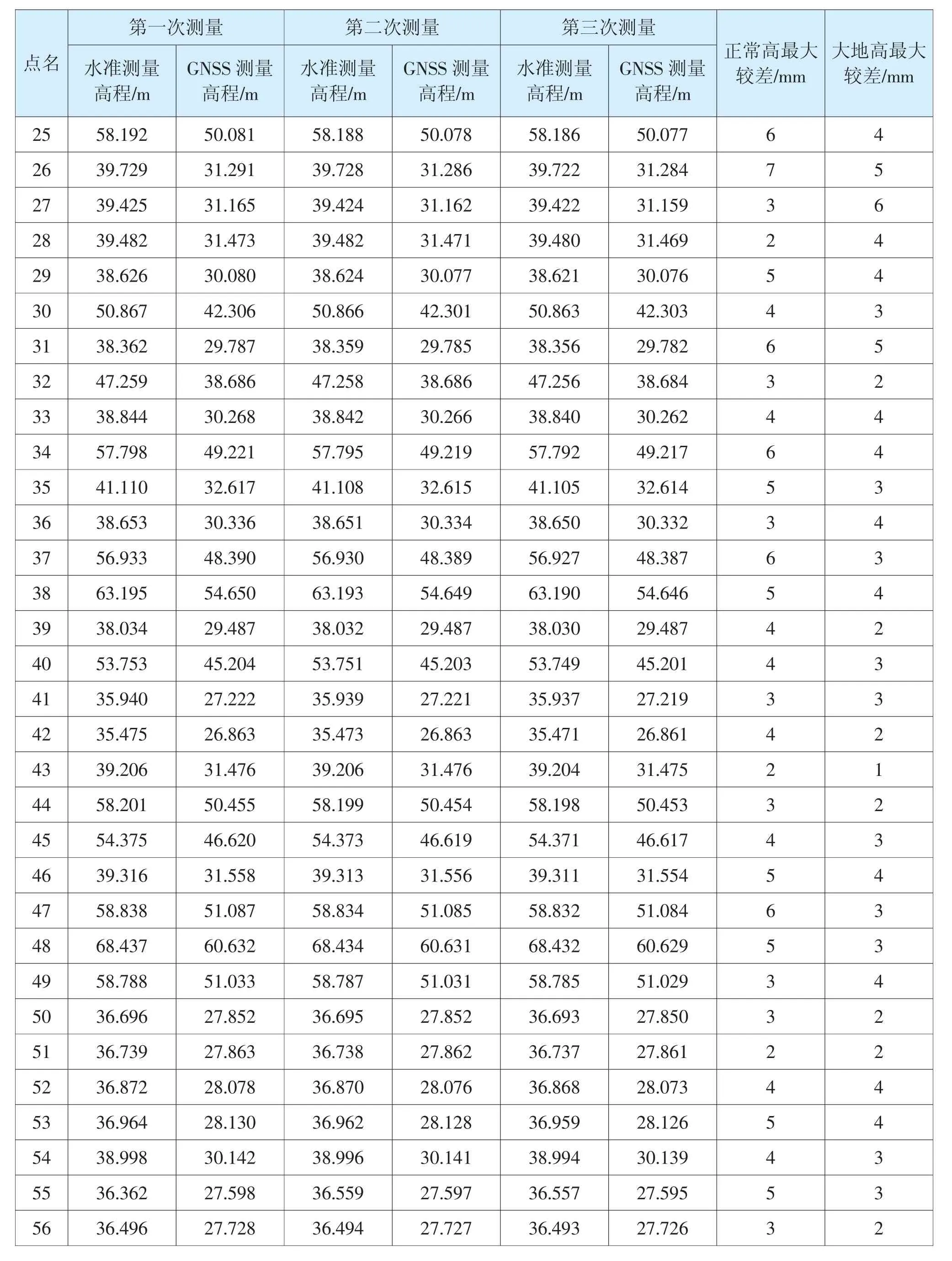
續：表1

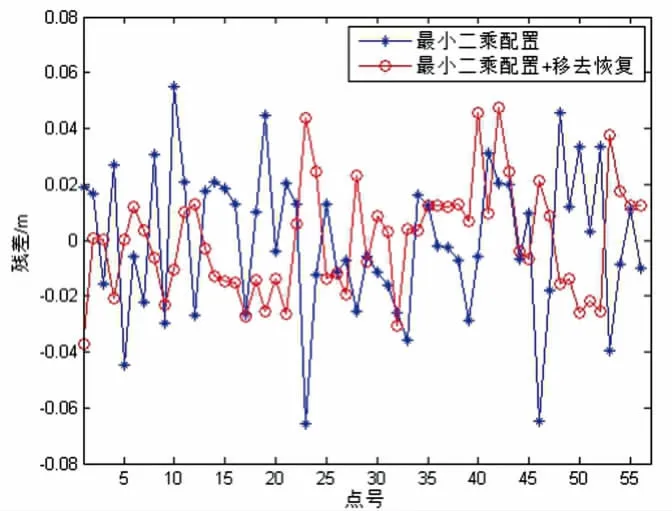
圖3 最小二乘配置殘差對比

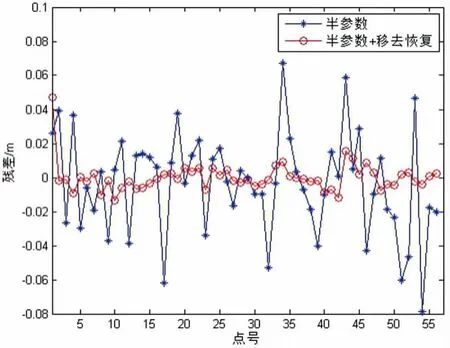
圖4 半參數殘差對比

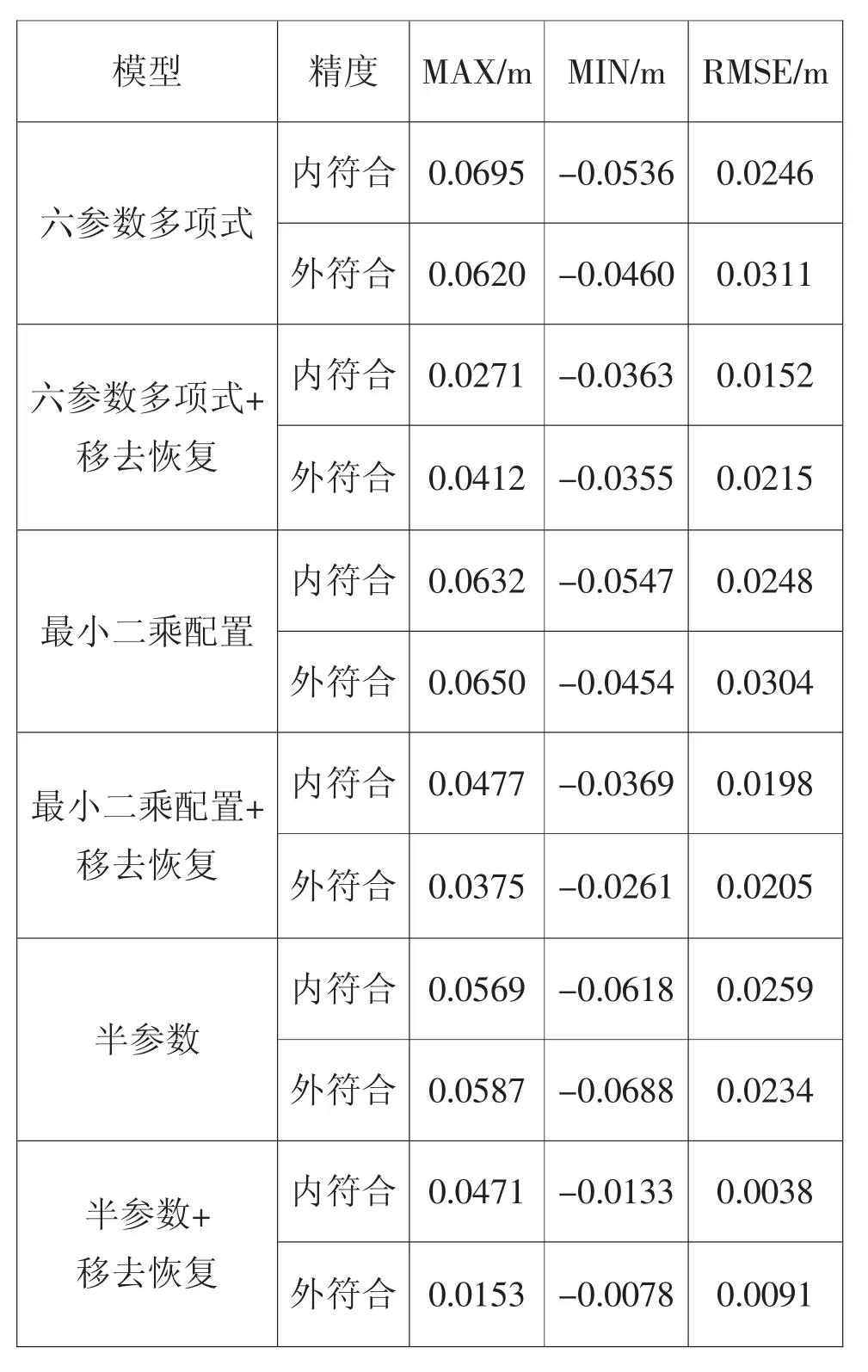
表2 計算結果

六種方案計算結果見表1，其中MAX 表示殘差最大值，MIN 表示殘差最小值，RMSE 表示內/外符合精度結果。 殘差對比（如圖3、圖4、圖5 所示）：由表2 可知，半參數+移去恢復方案內外符合精度均較小，分別為0.0038m 和0.0091m，六參數多項式模型內外符合精度較大，分別為0.0246m 和0.0311m；六參數多項式出現了最大內符合殘差，為0.0695m，最小二乘配置法出現了最大外符合殘差，為0.0650m，最小內外符合殘差均出現在半參數模型，為-0.0618m 和-0.0688m。若不加入移去-恢復技術，半參數模型相對比其他兩種模型并無明顯擬合優勢；最小二乘配置法相對六參數多項式的提升也比較有限。加入移去-恢復技術后半參數模型擬合精度提升比較明顯，內外符合精度均在毫米級，可以很好地用于實際測量工作中。

4.結束語

通過三種方案計算表明，移去恢復技術可以有效地提高高程異常擬合精度，但在多項式與最小二乘配置中提升有限，在半參數模型中提升較為明顯；半參數結合重力場模型的方案效果較好，最大內符合殘差為0.0.471m，最大外符合殘差為0.0153m，最小內符合殘差為-0.0133m，最小外符合殘差為-0.0078m，最適用于區域高程異常擬合。在實際應用中，若對高程異常求解要求精度不高，可直接采用多項式模型，其計算簡單、不需要使用重力數據可以快速計算待定點概略高程異常；若需要高精度高程異常則需使用半參數+移去恢復的方法，以獲得較好的擬合效果。