基底隔震的多層建筑結構自振頻率和振型解析

丁肇偉，陳龍珠，李慶來

(1.上海交通大學 船舶海洋與建筑工程學院 安全與防災工程研究所，上海 200240； 2.上海東浩蘭生(集團)有限公司，上海 200040)

地震是造成我國人員傷亡最為嚴重的一種自然災害。根據國內外科學研究和工程實踐的成果，我國于2001年修訂實施的《建筑抗震設計規范》(GB 50011-2001)，已涵蓋了抗震、隔震和消震3大類地震防御技術[1-3]。定性來說，抗震技術適用于各種建筑結構，隔震技術多用于剛度較大、高寬比較低的多層和高層建筑，而消震技術則適用于相對柔性的結構或結構中動力響應較大的部位。基底隔震技術是通過水平剛度低且具有一定阻尼的隔震器，在上部結構與基礎之間實現水平方向的柔性連接，使得由地基輸入上部結構的地震能量及其產生的加速度大為降低，結構層間位移大幅減小而不易損壞和坍塌，由此大幅提高建筑結構對強烈地震的防御能力。

我國自1994年建造首座采用橡膠支座的基底隔震示范建筑[4]以來，這個地震防御技術已得到了很好的推廣應用。在2008年5月汶川八級地震中，甘肅省隴南市武都區采用了基底隔震技術的北山郵政職工住宅樓完好無損，但鄰近普通的多層房屋結構墻體卻普遍出現了開裂[5]。四川省蘆山縣人民醫院門診綜合樓[6]，地上6層，局部地下1層，建筑設防類別為乙類，設防烈度為Ⅶ度(0.15g)，設計地震分組為第2組，中硬場地土，屬于Ⅱ類場地。2013年4月蘆山七級地震時，該樓隔震效果顯著，是我國到目前為止已被Ⅸ度實際地震考驗的隔震建筑。另一方面，早期建造的部分既有隔震建筑已出現不同程度病害，為了評價隔震層及隔震建筑動力特性現狀，需要研究此類建筑的檢測與鑒定方法[7]。

建筑隔震設計可采用地震反應譜法和時程分析法，前者涉及結構自振頻率和振型，后者需要采取數值積分計算[8]。在土木工程結構動力學中，對于多于3個自由度的建筑結構，自振頻率和振型的計算，因涉及高階超越方程而采用數值計算或近似簡化理論方法[9-10]求解，這對工程設計已不構成困難，但不便于直觀地了解自振頻率和振型受隔震層剛度、上部結構各層剛度和質量的影響方式。對在地基簡諧運動激勵下的多自由度結構，文獻[11]采用復數法直接得到了結構動力響應幅頻關系的解析解，由此可作為參數分析考察基底隔震層參數的變化對上部結構層間位移分布特性的影響規律。

三對角Toeplitz矩陣的主對角線和2個次對角線上的元素各自為一個常數，其余位置上的元素全為0。文中參考這種特殊矩陣的特征值和特征向量的解析求法[12-13]，先對多層建筑結構基底隔震層剛度取2個特定數值條件下的各階自振頻率和振型求得解析解，然后求其他數值的基底隔震層剛度，由此假設其各階自振頻率和振型的解析函數，再通過對數值計算結果的擬合分析，檢驗是否為自振頻率和振型的精確表達式。

1 特殊條件下結構自振頻率和振型解析解

圖1為模擬基底隔震的6層水平剪切型建筑結構計算簡圖。由于其底層下方設置了可水平向大幅變形的隔震層，該基底隔震的6層建筑結構在水平方向上具有7個自由度。假設各層樓板和屋面凝聚的質點質量相同(記為m)，上部結構各層的水平剛度相同(記為k)，隔震層剛度為αk，其中α為隔震層剛度比。改變α值，便可觀察基底隔震層剛度對隔震建筑結構自振頻率及其振型的影響。

圖1所示結構的特征方程可以表示為：

圖1 6層基底隔震建筑計算簡圖Fig.1 Calculation of six-story base-isolated building

(1)

式中：λ=ω2m/k，(ω為振動圓頻率)；φ為振型列陣。H為三對角矩陣：

由于三對角矩陣H，其主對角線上的元素并不全部相同，不是經典的Toeplitz三對角矩陣的形式。因此，對任意的α值，不能直接套用其特征值和特征向量的解析公式來求解結構各階自振頻率和振型。采用求解三對角Toeplitz矩陣特征值和特征向量的數學方法，式(1)難以得到解析解。作為一個特例，取α=1，則式(1)可以展開為遞推式和邊界條件：

(2)

對式(2)第1行的方程，試取其解為φj=rj，則有rj+1-(2-λ)rj+rj-1=0，經整理后得r2-(2-λ)r+1=0。記這個二元一次方程的2個根為r1和r2，則有：

r1+r2=2-λ，r1r2=1

(3)

所以，式(2)第1行的線性遞推式之解可表示為：

(4)

式中β1和β2為待定常數，j=1，2，…，7。

將式(4)代入式(2)第2行的2個邊界條件，得：

(5)

由式(3)、(5)得：

(6)

式(6)的解為：

(7)

將式(7)代入式(3)中的第1式，整理得：

(8)

從而得到當α=1時，圖1所示7自由度結構第s階自振圓頻率和振型的解析算式：

(9)

(10)

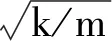
另一個特例，當α=0時(相當于6層建筑漂浮于水中)，經過上述類似推導，可得到該情況下，建筑物結構各階自振圓頻率和振型解析算式(s,j=1，2,…，7)：

(11)

(12)

2 任意基底隔震剛度下結構自振頻率和振型算式

改變基底隔震剛度數值，α乃至H中的主對角線第1個元素的數值發生變化，從而改變結構的自振頻率和振型，但此時卻不易求出它們的解析解。現根據上述2個特例的理論結果，對任意α值對應的各階自振頻率及其振型，嘗試采用如下表達形式：

(13)

(14)

上述2個嘗試性算式的誤差或適用性檢驗步驟如下：

1)利用常規數值方法，計算得到任意α值對應的結構自振圓頻率和振型；

3)將求出的θαs代入式(14)，得到嘗試的振型曲線，并將其與第1步中求得的振型曲線進行比較，由相對誤差大小來判定嘗試性算式的適應程度。

(15)

取α=0.03～1.0內的多個數值，經上述擬合分析得知，由數值方法計算的第1階自振圓頻率和式(13)求出的θα1(圖2，表1)以及用嘗試性算式(14)得出的第1階振型(圖3)，與數值方法所得結果的相關系數均大于0.999，表明式(13)～(15)是精確的表達式。

圖2 θα1～α關系曲線Fig.2 Relation curves of θα1～α

表1 θαs與α的關系Table 1 Relation of θαs and α rad

在圖3中，α=∞相當于一個6自由度的抗震結構。采用與上節α=1同樣的方法，可得其各階自振圓頻率和振型的解析算式：

圖3 第1階振型擬合曲線Fig.3 Fitting curves of the first mod

(16)

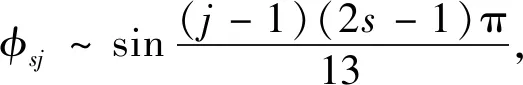
(17)

式(17)仍采用圖1的質點編號，取s=1便可繪制歸一化的第1階振型曲線。

由圖2可知，當α由1.0逐漸減小到約0.5時，θα1乃至基底隔震結構第1階自振圓頻率才會隨α的進一步減小而加速降低。由圖3可見，當α減小到0.3時，(Φ17-Φ11)已降低到抗震結構(α=∞)的1/2，而當α取為0.1時，(Φ17-Φ11)約只有抗震結構的1/4。因此，相對于上部結構的層間剛度，隔震層剛度必須足夠低，才可能使得上部結構的層間位移大幅降低而接近于剛體平移，從而提高上部結構的地震防御能力。

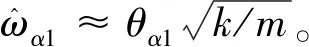
(18)

圖2虛線表明，式(18)擬合效果良好：α=0～0.7，相對誤差小于1%；在α=1處的相對誤差最大，但也低于3.1%。

(19)

將式(18)代入式(14)，則可方便地計算出基底隔震結構第1階振型。

對于α≤1.0，表1表明，各階自振圓頻率數值均未出現sin(0.5θαs)>1的無解問題，即式(13)、(14)適用。

3 結論

1)借用三對角Toeplitz矩陣特征值問題的求解方法，推導了2種特定的隔震層剛度條件下各階自振圓頻率和振型的解析解，由此構造的任意隔震層剛度條件下的結構各階自振圓頻率和振型的解析算式，并用數值解的結果進行了驗證。

2)鑒于其對基底隔震建筑結構的地震響應具有重要的影響，分析提出了第1階自振圓頻率和振型的簡化算式，具有較高的精度，可用于工程設計中選定隔震層剛度。

3)參數分析表明，當隔震層剛度比α<0.1時，上部結構第1振型的累積層間位移僅約為抗震結構的1/4，已向剛體平動靠近，有利于提高結構的地震防御能力。

本文理論分析的方法可用于求解具有其他層數的基底隔震建筑結構的各階自振圓頻率和振型。