負梯度泡沫金屬中的局部密實化現象

劉 冕，王根偉，宋 輝，王 彬

（1. 太原理工大學機械與運載工程學院應用力學研究所，山西 太原 030024；2. 材料強度與結構沖擊山西省重點實驗室，山西 太原 030024；3. 倫敦布魯內爾大學機械航空工程系，倫敦 UB8 3PH，英國）

多胞金屬兼具質輕和優異的吸能特性，已被廣泛用于高速火車、汽車和航空航天等領域。在準靜態下，多胞材料的應力-應變曲線呈現彈性、平臺和致密化3 個不同的變形階段[1-2]。在高加載速率下，多胞材料的動態行為可以通過應力增強和變形局部化來表征[3-5]。迄今為止，人們利用沖擊波理論和有限元方法來研究具有不同密度梯度的多胞材料，發現密度梯度對多胞動態響應下的力學性能具有重要影響[6-7]，不僅可以影響沖擊過程中應力波的傳播[8-9]，同時特定的梯度多胞金屬可以提高材料的能量吸收能力和抗沖擊性能[10-12]。

Reid 等[13]提出用一維剛性-塑性-鎖定(Rigid, perfectly-plastic, locking，R-PP-L)沖擊波模型來描述多胞材料中應力波的動態響應；隨后Tan 等[14]利用R-PP-L 模型對沖擊載荷下泡沫材料的動態壓縮性能進行了分析；Wang 等[15]通過R-PP-L 模型分析了線性密度梯度下多胞金屬的耐撞性，發現正梯度多胞金屬和負梯度多胞金屬分別對沖擊端和支撐端具有良好的保護效果；Shen 等[16-17]基于R-PP-L 模型研究了梯度多胞材料在高速壓縮時的沖擊響應，發現多胞材料沿正梯度方向壓縮時僅在加載端產生一個波陣面（單波模型），沿負梯度方向壓縮時則會在兩端各產生一個波陣面（雙波模型）。由于R-PP-L 模型僅包含平臺應力和鎖定應變兩個材料參數，只能實現材料應力-應變曲線的一階近似，為了更好地描述多胞材料的力學性能，Zheng 等[18]提出了一種更為精確的、率無關的剛性-塑性硬化（Rigid, plastichardening，R-PH）模型，用以表征梯度多胞材料的抗爆炸和抗沖擊特性[19-22]。

有限元模型常被用來研究梯度多胞材料的力學性能[23-25]。Ajdari 等[23]發現，功能梯度蜂窩結構存在3 種不同的壓潰模式：準靜態、過渡態和動態，沿沖擊方向降低相對密度可以增強蜂窩在壓潰初期的能量吸收；Fan 等[24]研究了均勻、梯度和隨機胞壁厚度的金屬空心球泡沫材料的動態破碎響應，發現負密度梯度泡沫具有最大的能量吸收能力，傳遞到受保護結構的力最小。Zhang 等[25]對受恒速沖擊影響下梯度Voronoi 多胞模型的動力學行為進行了模擬分析，定義了梯度多胞材料的第一、第二臨界速度。

梯度泡沫金屬在R-PH 模型下的應力波傳播研究大多集中于正梯度泡沫，對負梯度泡沫的沖擊波分析較少，負梯度泡沫沖擊波模型結果與有限元結果之間的聯系還有待完善。同時，負梯度泡沫材料雖然具有防護支撐端被保護物體且能量吸收能力較強的特點，但支撐端局部密實化現象的發生影響了負梯度泡沫優異的力學性能，因此，局部密實化的影響因素值得分析。

本研究基于R-PH 模型，建立恒速沖擊荷載作用下負梯度泡沫材料的一維沖擊波模型，給出沖擊波傳播的基本控制方程；利用隨機Voronoi 技術構建梯度泡沫金屬材料的三維細觀有限元模型，使用LSDYNA 有限元軟件對泡沫金屬的動態壓潰過程進行模擬分析，用于驗證沖擊波理論結果；通過分析沖擊模型的響應歷程，定義梯度泡沫材料的局部密實化應變和第二臨界速度，并計算不同密度梯度、相對密度下局部密實化應變、第二臨界速度的變化規律；最后討論負梯度泡沫中支撐端局部密實化現象對被保護結構的影響，為工程防護提供參考。

1 理論與方法

1.1 沖擊波模型

負梯度泡沫的一維沖擊波模型如圖1 所示，質量為M 的物塊以恒定的中等沖擊速度v 撞擊閉孔梯度泡沫金屬試件，試件的兩端同時產生沖擊波，且沖擊波朝著相反的方向傳播，此為雙波模型。將沖擊端處產生的沖擊波定義為前沖擊波，支撐端處產生的沖擊波定義為后沖擊波，前、后沖擊波的物理量分別用下標f 和b 表示，在t 時刻，沖擊波陣面的拉格朗日坐標分別為Xf(t)、Xb(t)。在波陣面處，波陣面前、后的物理量分別為{vA(t)，εA(t)，σA(t)}、{vB(t)，εB(t)，σB(t)}，兩個沖擊波陣面之間未變形區域的速度為vu(t)。

定義負梯度泡沫在拉格朗日坐標下的密度分布為

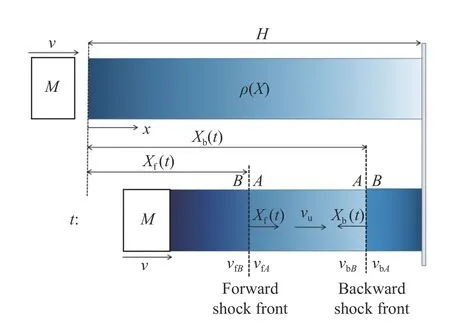
圖 1 雙波模型Fig. 1 Double shock model

式中：ρ0為平均相對密度，γ 為密度梯度，X 為x 方向的拉格朗日坐標，H 為梯度試件x 方向的總長度。

根據應力波理論[26]，沖擊波陣面上的運動學相容條件為

同時，動力學相容條件為

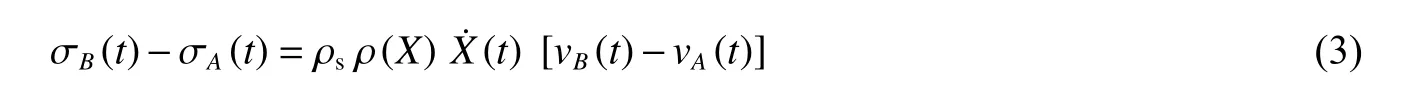
式中：ρs為基體材料密度。聯立式(2)、式(3)可得波后應力為

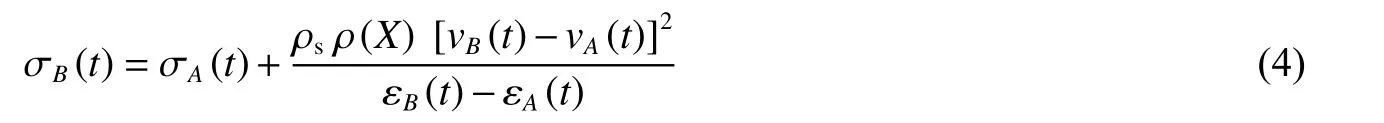
前波波陣面的初始條件為{vfA(t) = vu(t)，εfA(t) = 0，σfA(t)}，{vfB(t) = v，εfB(t)，σfB(t)}，后波波陣面上的初始條件為{vbA(t) = vu(t)，εbA(t) = 0，σbA(t)}，{vbB(t) = 0，εbB(t)，σbB(t)}。

將初始條件代入式(4)，可得前、后波陣面處波后應力為

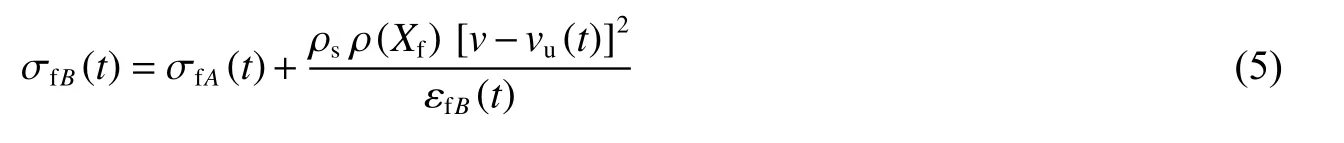
基于R-PH 模型的剛性假設

近年來，人工造林已成為造林的主要方式，忽視了天然林自我更新和人工促進森林自我更新的重要互補作用。隨著國家生產和建設對木材資源的需求日益增加，森林采伐遵循“消費少于增長”的原則，導致人工造林的更新不能滿足林業良性發展和管理的需要。追求人工造林成果，不注意森林的自然更新，是造林方式的一大缺陷。

式中：σ0為泡沫材料準靜態的初始壓潰應力，C 為應變硬化參數，ε 為應變。波陣面的前方區域接近塑性壓潰臨界狀態，且處于應力平衡場，因此波陣面處兩種波前應力分別為

由此推出，波后應變為

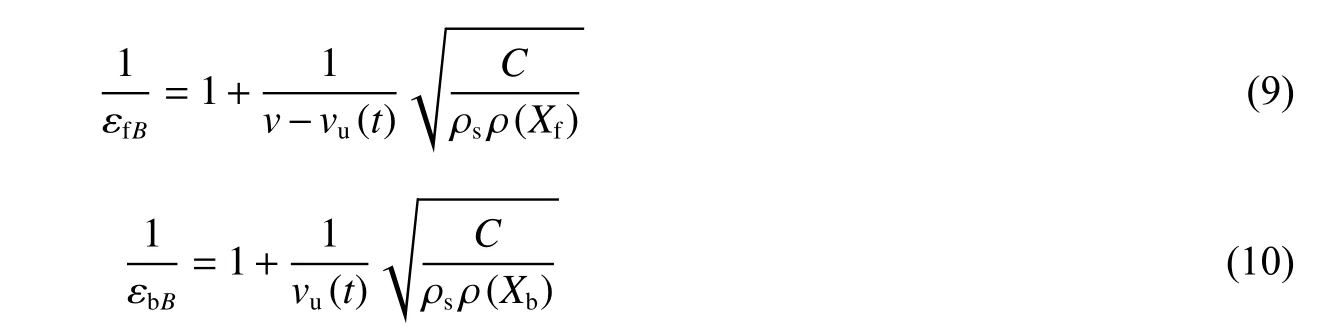
以中間未變形區域為研究對象，由牛頓第二定律可得

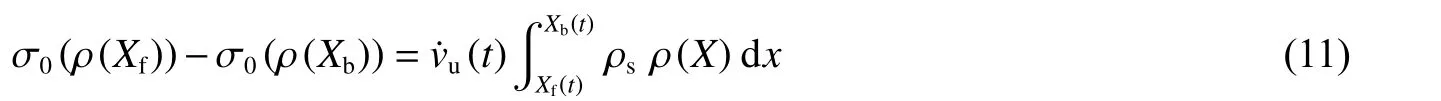
積分后，未變形區域速度為

因此前、后波陣面的坐標為

在沖擊波傳播過程中，當vu= v，即中間未變形區域的速度增大到沖擊速度時，前沖擊波停止傳播，定義此時刻為t*。當t ＜ t*時，定義為第一階段，沖擊波在該階段的響應結果可由上述所得方程求解。當t ＞ t*時，第二階段開始，只有單一的后沖擊波向左端沖擊端繼續傳播。當后波陣面與前波陣面相遇時，響應結束，定義此時刻為t2，則第二階段后波陣面的坐標為

波后應力為

結合上述方程，雙波模型中沖擊端應力σimp與支撐端應力σsta分別為

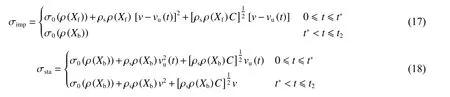
1.2 有限元模型

3D-Voronoi 模型是由N 個形核點完全隨機分布在體積為V0的立方體區域內生成的，為了防止模型中產生過小胞元，立方體內任意兩個相鄰形核點之間的距離不小于δ[27]

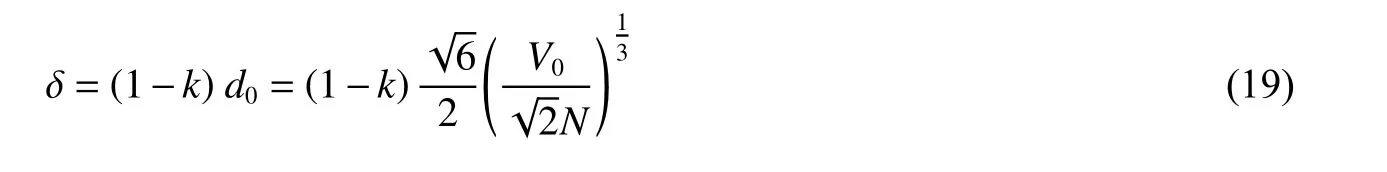
本研究中模型的平均相對密度ρ0分別為0.06、0.09、0.12，密度梯度γ 分別為-0.4、-0.6、-0.8，尺寸為40 mm × 40 mm × 60 mm，不規則度為0.5，模型胞元個數分別為700（γ = -0.4）、732（γ = -0.6）和768（γ = -0.8），胞壁厚度由給定的相對密度確定。經有限元收斂分析后，使用S3R 和S4R 殼單元混合網格對泡沫模型進行劃分，網格尺寸設置為0.2 mm[28]。以ρ0= 0.09、γ = -0.8 為例，負梯度泡沫金屬的3D-Voronoi 有限元模型如圖2 所示，運用LS-DYNA 軟件進行數值模擬。在右端固定一個剛性板，左端剛性板以恒定的沖擊速度撞擊泡沫模型。基體材料為鋁，選定雙線性應變強化本構模型，模型參數見表1。其中，ρs為密度，E 為楊氏模量，ν 為泊松比，σys為屈服應力，Et為切線模量。定義泡沫模型為自接觸，兩端剛性板和泡沫模型之間為面面接觸，設定動摩擦系數為0.2。

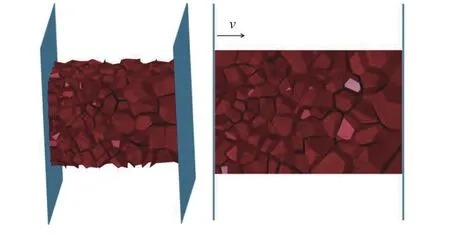
圖 2 有限元模型Fig. 2 Finite element model

表 1 本構模型參數Table 1 Constitutive model parameters

1.3 R-PH 模型的材料參數

R-PH 模型中初始壓潰應力σ0、硬化參數C 與相對密度之間存在冪律關系[29]

式中：k1、k2為擬合參數。如圖3 所示，在5 m/s 恒速壓縮條件下，用最小二乘法擬合不同相對密度的三維均勻Voronoi 泡沫模型的名義應力-應變曲線，得到k1、k2分別為1.25、0.12。

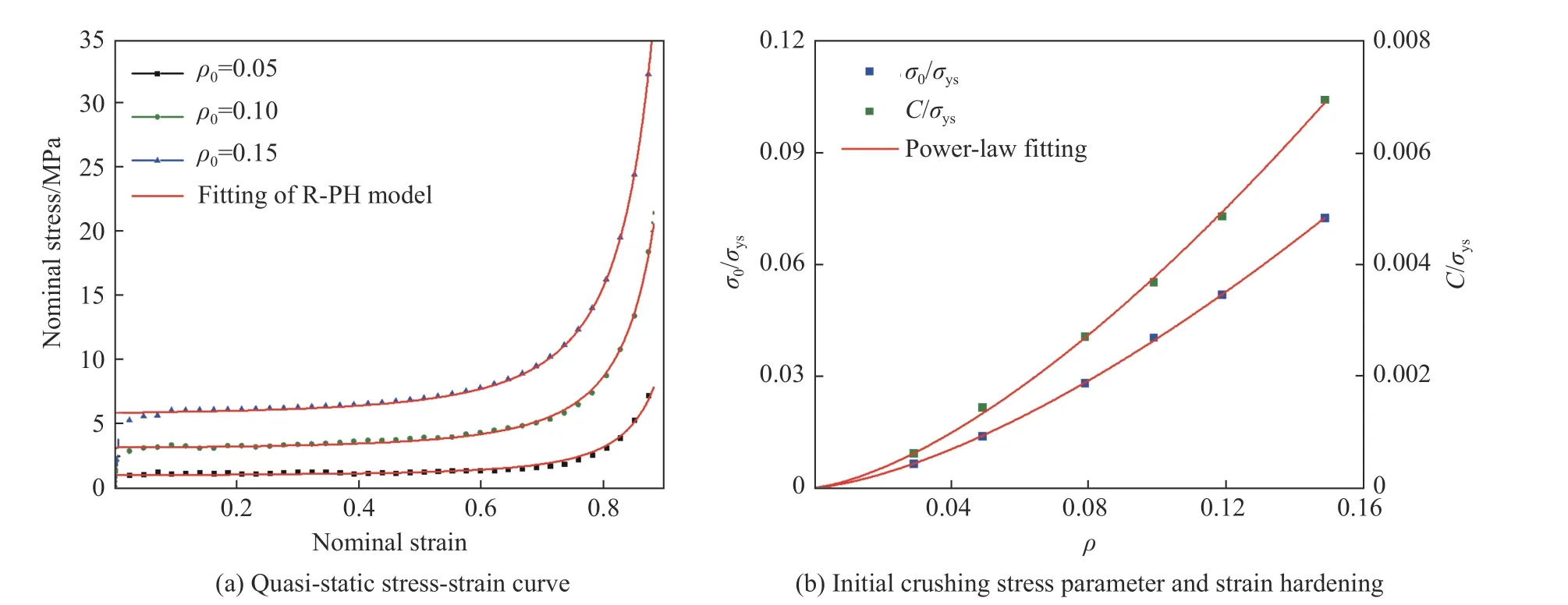
圖 3 不同相對密度的準靜態應力-應變曲線和參數擬合結果Fig. 3 Quasi-static stress-strain curve and parameter fitting results with different relative densities

沖擊波控制方程的初始條件為vu(0) = 0，Xf(0) = 0，Xb(0) = H，這是非線性微分方程組，沒有顯式解，因此采用四階Runge-Kutta 法進行求解。

2 結果和討論

2.1 沖擊波歷程

兩種沖擊速度下vu的變化曲線如圖4 所示，對應的波陣面位置如圖5 所示。由圖4 和圖5 可以看出，當沖擊速度較低(v = 50 m/s)時，t ＜ t*（第一階段），隨著vu逐漸增大，前波陣面坐標Xf由零逐漸增加，后波陣面坐標Xb由H = 60 mm 處開始逐漸減小；當vu增大到50 m/s 時，t = t*，前沖擊波陣面停止傳播；當t*＜ t ＜ t2時，后沖擊波陣面繼續傳播；在t2時刻，后波陣面到達前波陣面位置，響應結束。當沖擊速度較高(v = 150 m/s)時，前沖擊波始終存在，且傳播距離變大，t*不再存在；在t2時刻，前后波陣面相遇，此時未變形區域的速度vu小于150 m/s。

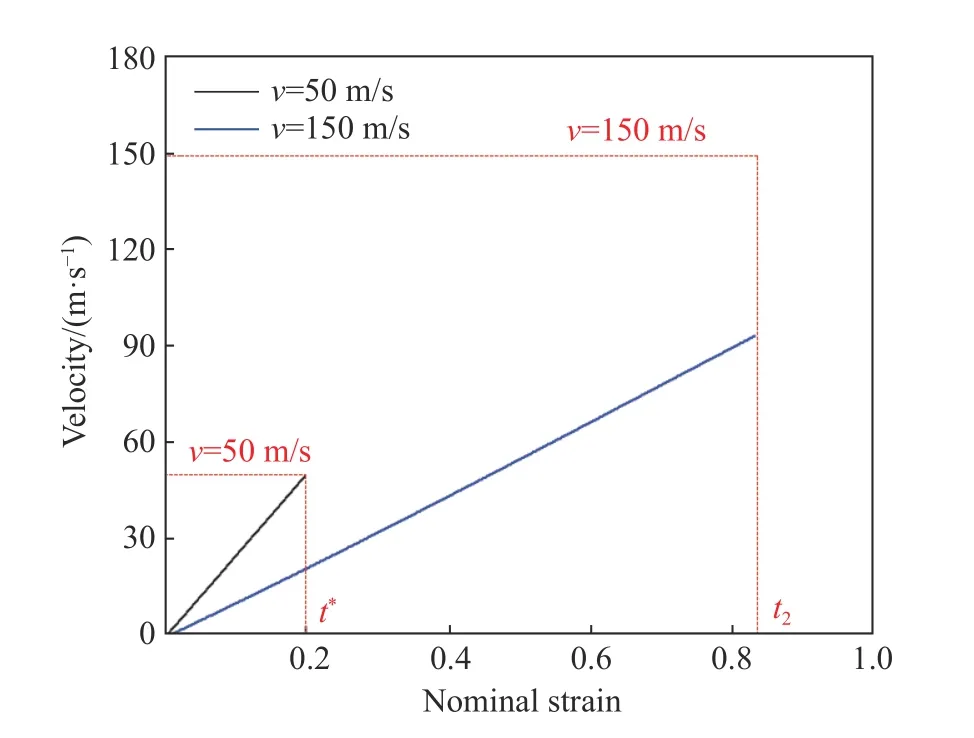
圖 4 不同沖擊速度下的vu 曲線Fig. 4 Curves ofvu at different impact velocities

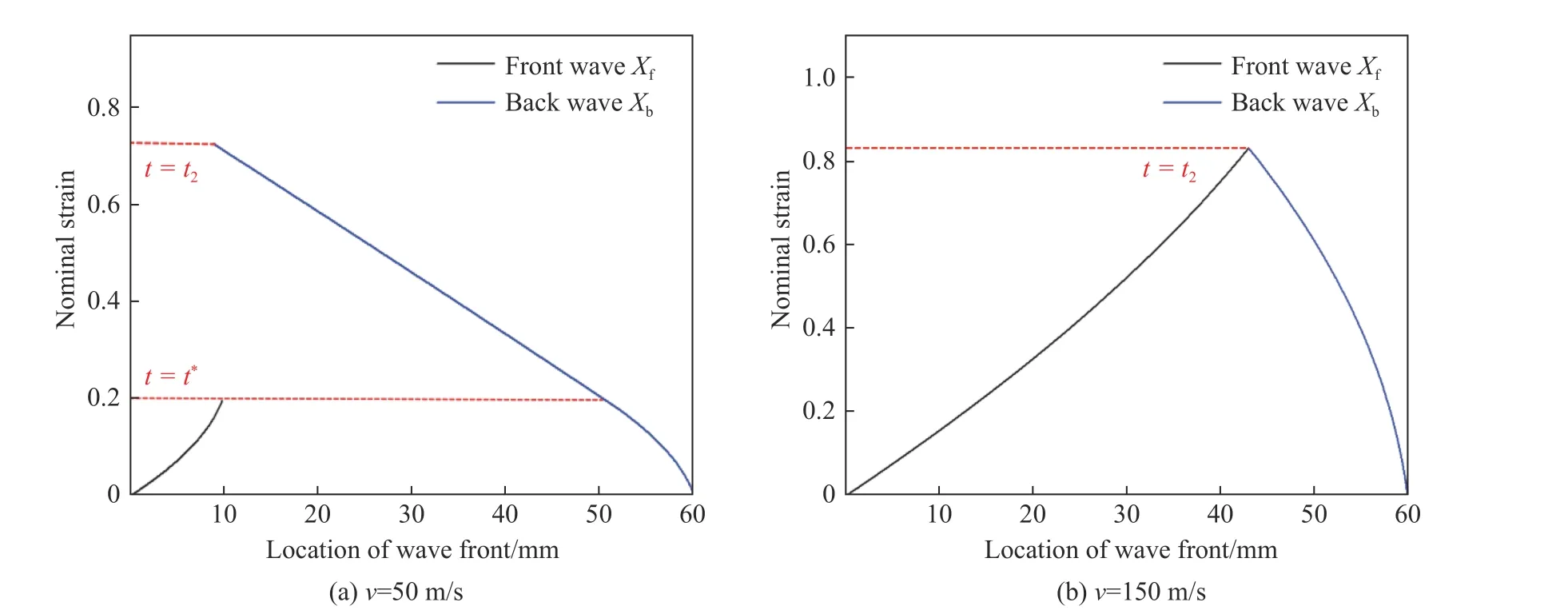
圖 5 不同沖擊速度下波陣面的位置曲線Fig. 5 Location of wave front at different impact velocities

2.2 局部密實化應變與第二臨界速度

在負梯度泡沫的變形過程中會發生支撐端的局部變形，局部變形結束時的現象稱之為支撐端的局部密實化，該時刻所產生的應變定義為局部密實化應變[30]。局部密實化應變可以通過能量吸收效率曲線來定義。能量吸收效率[31]是指材料壓縮至某一名義應變時所吸收的能量與對應的名義應力的比值，其表達式為

式中：η 為能量吸收效率，εy為初始峰值應力時的應變，ε 為材料壓縮時的名義應變，σ(ε)為材料壓縮至名義應變時所對應的名義應力。

負梯度泡沫的名義應力-應變曲線與能量吸收效率曲線如圖6 所示。由圖6 可知，能量吸收效率曲線呈現先上升后下降的趨勢，曲線到達最高點時對應的應變為局部密實化應變，此刻沖擊端曲線到達屈服應力后的最低點。到達局部密實化應變后，沖擊端應力值開始上升，能量吸收效率曲線開始下降。

在不同的沖擊速度下，負梯度泡沫存在準靜態模態、過渡模態和沖擊模態3 種變形模態[32]，其中過渡模態和沖擊模態分別對應兩種沖擊波傳播歷程。第二臨界速度vcr2[33]是指過渡模態向沖擊模態轉變的臨界速度。圖7、圖8 分別是相對密度為0.09、密度梯度為-0.8 的梯度泡沫在兩種模態下的應變云圖與名義應力-應變曲線。

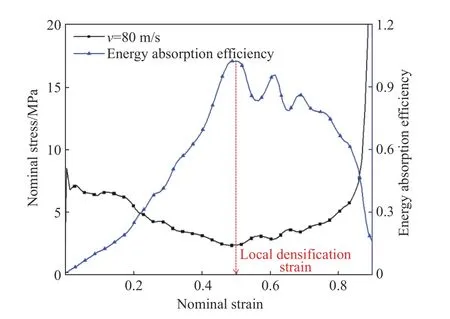
圖 6 負梯度泡沫的名義應力-應變曲線與能量吸收效率曲線Fig. 6 Nominal stress-strain curve and energy absorption efficiency curve of negative graded foam

圖 7 負梯度泡沫的應變云圖Fig. 7 Strain nephograms of negative graded foam

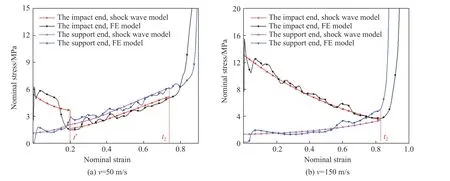
圖 8 兩端應力的FE 結果和理論預測對比Fig. 8 Comparison of FE results and theoretical predictions at both sides stress

由圖7、圖8 可知，沖擊波模型推導出的理論應力值與有限元模型的模擬結果吻合較好，理論模型能夠較好地預測負梯度泡沫在沖擊載荷作用下的應力變化趨勢。若泡沫處于過渡模態(v = 50 m/s ＜vcr2)：在沖擊波第一階段，負梯度泡沫兩端同時發生變形；當t = t*時，沖擊端停止變形，應力突然下降，小于此處的準靜態屈服應力，此時支撐端局部變形結束，t*時刻所對應的應變為局部密實化應變；隨后支撐端繼續向中間區域變形，兩端應力逐漸上升。若泡沫處于沖擊模態(v = 150 m/s ＞ vcr2)：慣性效應改變了泡沫的變形特性，在壓縮過程中，泡沫主要在沖擊端發生變形；當t = t2時，沖擊波陣面相遇，支撐端的局部變形結束，t2所對應的應變為局部密實化應變。當v = vcr2時，未變形區域速度vu(t)達到沖擊速度v 的時刻剛好等于兩波陣面相遇時刻，故t*= t2時所對應的沖擊速度為第二臨界速度vcr2。

2.3 參數分析

沖擊波理論模型與有限元模型得到的局部密實化應變隨密度梯度和相對密度變化的曲線如圖9所示。由圖9 可知，兩種模型計算結果的最大誤差小于15%，說明沖擊波理論模型能夠較好地預測負梯度泡沫中的局部密實化應變。在不同沖擊速度下，局部密實化應變存在3 個增長趨勢：當沖擊速度較小時，局部密實化應變隨沖擊速度的增加緩慢增大；當沖擊速度中等時，局部密實化應變增長幅度上升；當沖擊速度較高且超過第二臨界速度時，局部密實化應變增長逐漸平緩且無限接近壓實應變。通過比較相同沖擊速度下密度梯度與相對密度對局部密實化應變的影響發現，隨著密度梯度絕對值和相對密度的增大，局部密實化應變逐漸減小，且密度梯度對局部密實化應變的影響比相對密度更大。

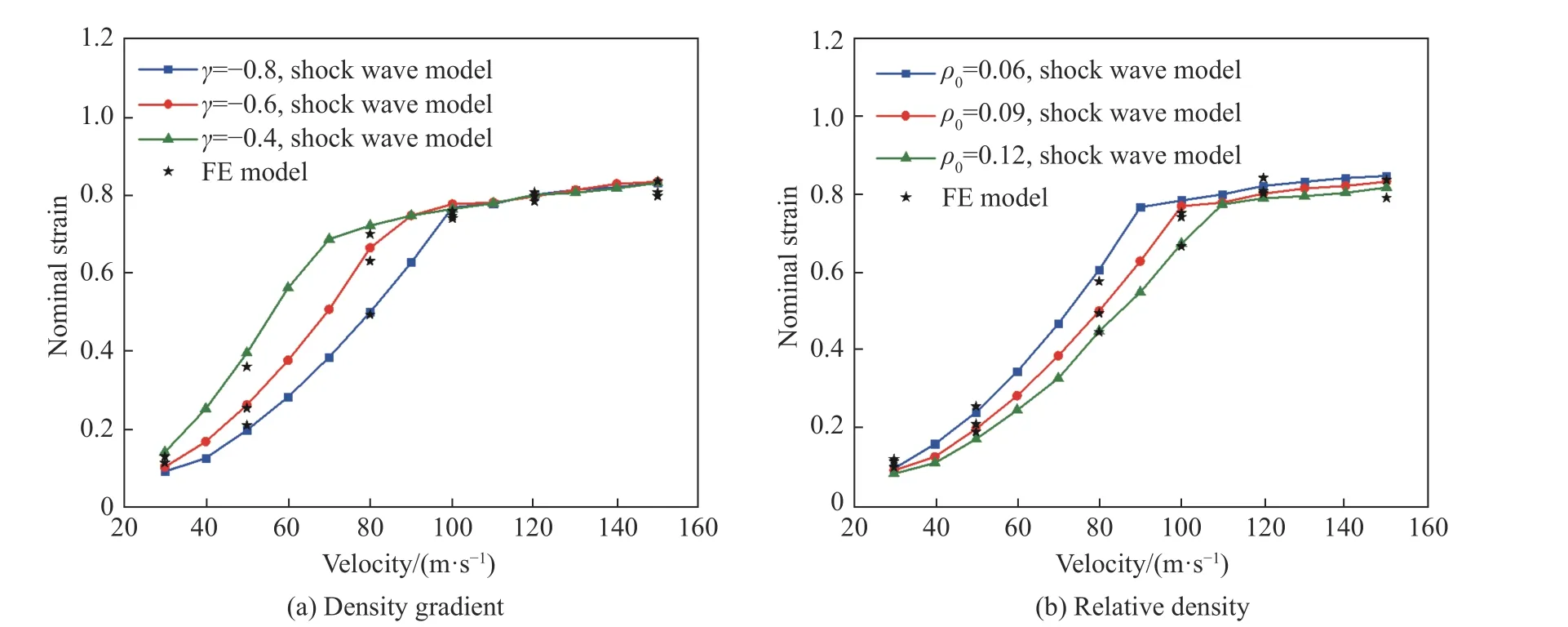
圖 9 密度梯度與相對密度對局部密實化應變的影響Fig. 9 Influence of density gradient and relative density on local densification strain

不同密度梯度和相對密度下負梯度泡沫的變形模態如圖10 所示，第二臨界速度將負梯度泡沫的變形模態圖分為兩個區域，分別對應速度中等時的過渡模態和速度較高時的沖擊模態。從圖10 可以看出，更大的密度梯度和相對密度會延遲泡沫模態的轉變，隨著密度梯度絕對值和相對密度的增加，由過渡模態向沖擊模態轉變所需的速度越高，第二臨界速度越大。

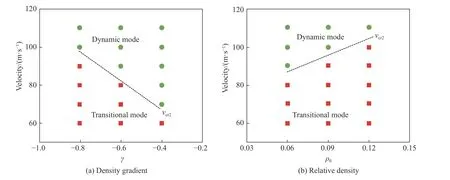
圖 10 不同密度梯度和相對密度下的變形模態Fig. 10 Deformation modes under different density gradients and relative densities

2.4 局部密實化的影響

圖11 給出了兩種速度下密度梯度和相對密度不同時支撐端的應力-應變曲線。為了消除相對密度大小對應力增長幅度的影響，圖11(b)和圖11(d)中，用支撐端應力分別除以對應的相對密度。由圖11可以看出，密度梯度和相對密度對支撐端具有顯著影響。密度梯度絕對值越大，泡沫的初始屈服應力越小；相對密度越大，泡沫的應力值越大；密度梯度絕對值和相對密度越大的泡沫，支撐端應力值增長越早，且應力增長幅度越大。當v = 50 m/s 時，γ = -0.8 和ρ0= 0.12 的梯度泡沫最早發生應力增長，且擁有最大的應力增長值；當v = 150 m/s 時，支撐端平臺階段變長，應力逐漸平穩，γ = -0.4 的梯度泡沫應力增長現象消失，而其他梯度泡沫的后期應力仍有增加。

圖 11 不同沖擊速度下支撐端的名義應力-應變曲線Fig. 11 Nominal stress-strain curve of the support end under different impact velocities

圖12 為相對密度為0.09、密度梯度為-0.6 的梯度泡沫有限元模型在不同沖擊速度下沖擊端與支撐端的名義應力-應變曲線。當沖擊速度為30 m/s 時，局部密實化應變為0.11，當變形到達局部密實化應變后，負梯度泡沫的沖擊端與支撐端應力曲線上升，其中支撐端應力值由2.1 MPa 持續上升到5.3 MPa；隨著沖擊速度的增加，局部密實化應變逐漸增大，沖擊端應力上升值減小，而支撐端的應力增長明顯，應力增長幅度加大；當沖擊速度為80 m/s 時，在局部變形過程中，支撐端應力值逐漸上升，最高上升到6.6 MPa；當沖擊速度超過第二臨界速度，泡沫進入沖擊模態，沖擊端應力值在初始峰值應力后始終處于逐漸下降的變化過程，支撐端應力值逐漸平穩。

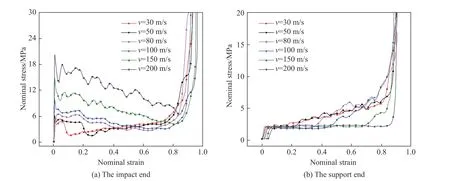
圖 12 不同沖擊速度下沖擊端與支撐端的名義應力-應變曲線Fig. 12 Nominal stress-strain curves of the impact end and the support end under different impact velocities

支撐端的局部密實化現象導致被保護物體受到較高強度的載荷，影響了負梯度泡沫優異的抗沖擊性能，對被保護物體不利。在保證能量吸收滿足沖擊載荷作用的前提下，適當地減小相對密度和密度梯度，能延緩支撐端應力值的增長；同時，沖擊速度高于第二臨界速度可使支撐端處于應力平臺狀態，確保被保護物體在壓縮過程中承受較小的載荷。因此，可以利用由沖擊波理論得到的局部密實化應變與第二臨界速度，有效地預測負梯度泡沫在不同材料參數下兩端應力值增長對應的變形范圍和速度范圍，改善不同工況下負梯度泡沫材料作為抗壓材料的防護效果。

3 結 論

利用R-PH 理論設計了恒速沖擊載荷下負梯度泡沫材料的一維沖擊波模型，推導了沖擊波傳播的基本控制方程。利用LS-DYNA 有限元軟件對三維Voronoi 有限元模型計算模擬得到的結果，對沖擊波的理論分析進行驗證。根據沖擊波理論定義了局部密實化應變和第二臨界速度，并探討了沖擊速度、密度梯度、相對密度參數的影響，得到如下結論。

(1) 沖擊波模型的理論解與有限元模型的數值解吻合較好，基于R-PH 模型的沖擊波理論能較好地預測負梯度泡沫金屬的應力-應變曲線、局部密實化應變和第二臨界速度。

(2) 局部密實化應變存在3 個增長過程：當速度較小時應變增長比較緩慢，當速度中等時應變快速增長，當速度較高時應變增長逐漸平緩；密度梯度絕對值與相對密度越大，局部密實化應變越小，且支撐端的應力增長現象越早發生，應力增長越多。

(3) 密度梯度絕對值與相對密度越大，第二臨界速度越大；當沖擊速度小于第二臨界速度時，速度越大，支撐端的應力增長越多；當沖擊速度大于第二臨界速度時，速度越大，支撐端的曲線越平穩。